GUIA 1 NOVENO EFA MAGNITUDES - Over-blog
Anuncio
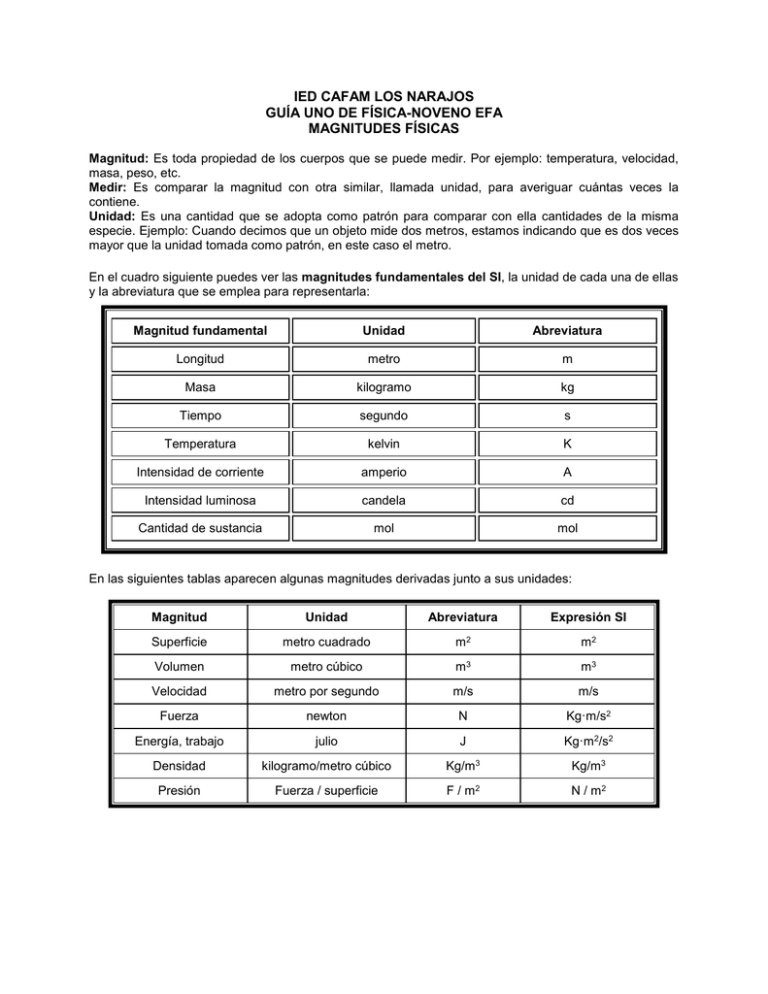
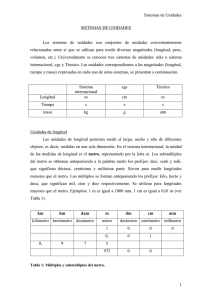
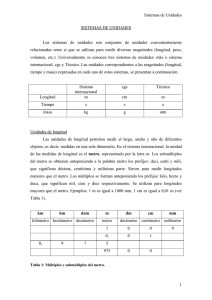
IED CAFAM LOS NARAJOS GUÍA UNO DE FÍSICA-NOVENO EFA MAGNITUDES FÍSICAS Magnitud: Es toda propiedad de los cuerpos que se puede medir. Por ejemplo: temperatura, velocidad, masa, peso, etc. Medir: Es comparar la magnitud con otra similar, llamada unidad, para averiguar cuántas veces la contiene. Unidad: Es una cantidad que se adopta como patrón para comparar con ella cantidades de la misma especie. Ejemplo: Cuando decimos que un objeto mide dos metros, estamos indicando que es dos veces mayor que la unidad tomada como patrón, en este caso el metro. En el cuadro siguiente puedes ver las magnitudes fundamentales del SI, la unidad de cada una de ellas y la abreviatura que se emplea para representarla: Magnitud fundamental Unidad Abreviatura Longitud metro m Masa kilogramo kg Tiempo segundo s Temperatura kelvin K Intensidad de corriente amperio A Intensidad luminosa candela cd Cantidad de sustancia mol mol En las siguientes tablas aparecen algunas magnitudes derivadas junto a sus unidades: Magnitud Unidad Abreviatura Expresión SI Superficie metro cuadrado m2 m2 Volumen metro cúbico m3 m3 Velocidad metro por segundo m/s m/s Fuerza newton N Kg·m/s2 Energía, trabajo julio J Kg·m2/s2 Densidad kilogramo/metro cúbico Kg/m3 Kg/m3 Presión Fuerza / superficie F / m2 N / m2 Para un mejor estudio de los fenómenos fiscos en sus medidas es necesario considerar los múltiplos y submúltiplos de las unidades del SI descritos en la siguiente tabla: Múltiplos y submúltiplos de las unidades del SI Múltiplos Submúltiplos Prefijo Símbolo Potencia Prefijo Símbolo Potencia giga G 109 deci d 10-1 mega M 106 centi c 10-2 kilo k 103 mili m 10-3 hecto h 102 micro µ 10-6 deca D 101 nano n 10-9 1.1. EQUIVALENCIAS ENTRE UNIDADES FUNDMENTALES Y SUS MÚLTIPLOS: Para un mejor estudio de los fenómenos físicos es necesario comprender y utilizar los múltiplos y submúltiplos de las unidades fundamentales que se relacionaron en la tabla anterior y para establecer su equivalencia debemos tener en cuenta su valor exponencial para convertir de una unidad a un múltiplo o submúltiplo y viceversa, así: Al convertir un múltiplo a una unidad o submúltiplo se debe multiplicar por la suma de los exponenciales (sin tener en cuenta los signos) que hay del múltiplo hasta la unidad o submúltiplo pedido: Ej 1: Al convertir kilo (103) a centi (10-2) se debe multiplicar por 105 3 kilogramos a centigramos = 3 x 105 = 3 x 100.000= 300.000 centigramos Ej. 2: Al convertir mega (106) a micro (10-6) se debe multiplicar por 1012 5,25 megámetros a micrómetros = 5,25 x 1012 = 5,25 x 1.000.000.000.000 = 5.250.000.000.000 micrómetros Al convertir un submúltiplo a una unidad o múltiplo se debe dividir por la suma de los exponenciales (sin tener en cuenta los signos) que hay del submúltiplo hasta la unidad o múltiplo pedido o multiplicarlo por ese exponencial pero negativo (cuando se trabaja con calculadora): Ej 1: Al convertir mili (10-3) a hecto (102) se debe dividir entre 105 o multiplicar por 10-5 6 milímetros a hectómetros = 6 x 10-5 = 6 / 100.000 = 0,00006 hectómetros Ej 2: Al convertir deci (10-1) a kilo (103) se debe dividir entre 104 o multiplicar por 10-4 2,4 decigramos a kilogramos = 2,4 x 10-4 = 2,4 / 10.000 = 0,0024 kilogramos Nota: también se pude utilizar la regla de tres para realizar las conversiones así por ejemplo Convierte a la menor unidad: 3 kg 5 hg 6 dag 2 g ACTIVIDAD 1 1. El milímetro en el sistema métrico, puede clasificarse como: ¿unidad fundamental o unidad variada? ¿Porque? 2. Convierte: a) 12 km a metros. b) 7 000 mm a metros. c) 80 hm a kilómetros. d) 5 x 106 cm a kilómetros e) 1.2 x 1015 cm a kilómetros. f) 560.8 Dm a hectómetro. 3. Convierte a) 8 cm 3 mm a metros. b) 15 m 78 cm a decámetros. c) 9 km 3 Dm a metros. d) 17 Dm 3 m 8 dm a centímetros. 4. Cuánto cuestan 15.2 m de tela si el dm se vende a $125 pesos. 5. Un terreno para pastar, de forma cuadrada, tiene 305 dm de lado. Si se quiere cercar con cinco líneas de alambre. ¿Cuán metros de alambre se necesitarán? 6. ¿Qué parte de una hectárea ocupa el terreno destinado a pastar? 7. En qué unidad será más conveniente medir: a) La distancia entre dos ciudades. ______________________________ b) El largo del aula. _______________________________ c) EL largo del lápiz. _______________________________ 8. Dos automóviles salen de dos provincias de Cuba que están en la misma dirección, en sentido contrario y a 370 km de distancia. Uno de los automóviles iba a una velocidad menor que el otro. Al cabo de tres horas uno había recorrido 12 117 000 cm y el otro 123 000 m. ¿Cuánto les faltan por recorrer? 9. Dos estaciones de trenes distan 720 km. En un dibujo representativo estas estaciones distan 9,0 m, entonces, ¿cuál será el alcance real entre otras dos ciudades de 2,5 dm en ese mismo dibujo? 10. La casa de Susana dista 1 km 4 hm 6 Dm de la Universidad Cafam. Cada día Susana recorre esta distancia dos veces. ¿Cuál es la distancia en metros que recorre diariamente? 11. Una carrera ciclística comprende tres etapas y su recorrido total es de 725 km. La primera etapa comprende 2.4 x 104 m y la segunda es de 31 500 Dm. ¿Cuál es la distancia a recorrer en la tercera etapa? 12. De un rollo de alambre que tiene 45 m, se venden sucesivamente 5,4 m, 80 cm, 170 dm y 1 200 mm. ¿Cuántos metros quedan en el rollo? 13. Un joven recorre un cuarto de distancia entre dos ciudades a pie, un quinto en bicicleta y los 55 km en tren. ¿Cuál es la distancia entre las dos ciudades? 14. El perímetro del triángulo que se muestra en la figura es: 15. Completa la siguiente tabla realizando las conversiones indicadas: Cantidad Convertir en 8 kg g 8,561 dg Kg 7g kg 200 m km 2 cm m 20 km m 8 cc l 10 ml l 6,45 Mm mm 10 l cc 20 l ml 980 g / cm kg / m 20 km / h m/s 20 m / s km / h 20 cm / s km / h Operación Respuesta(número y unidad)