Mecanismos de transporte eléctrico en películas delgadas de ITO
Anuncio

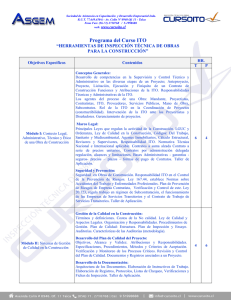
Revista Colombiana de Física, vol. 41, No. 2, Abril 2009 Mecanismos de transporte eléctrico en películas delgadas de ITO (SnO2:In) Electric transport mechanisms in indium tin oxide thin films H. Méndez, C. Hernández, N. Ulloa, J.C. Salcedo y H. Rodriguez Grupo de Películas Delgadas, Pontificia Universidad Javeriana. Recibido XXXX; Aceptado XXXX; Publicado en línea XXXX Resumen Películas delgadas de óxido de estaño dopado con indio (SnO2:In), material conocido como ITO por su sigla en inglés, fueron caracterizadas por medidas de resistividad eléctrica y movilidad Hall en el rango de temperaturas 14K-400K. Este material posee baja resistividad (~10-4 Ωcm), la cual se incrementa ligeramente con la temperatura, y una alta densidad de portadores (η= 4,0 ± 1,1 × 1019 cm-3) que se mantiene aproximadamente constante en el rango de temperatura indicado. Estos resultados permiten concluir que se trata de un semiconductor degenerado con huecos actuando como portadores mayoritarios. Parámetros importantes del semiconductor fueron obtenidos por simulación de la contribución fonónica a la resistividad del material. Palabras claves: ITO, OLEDs, HOMO, LUMO, resistividad eléctrica, movilidad Hall, ley de Bloch-Grüneisen, fonones. Abstract Resistivity and Hall mobility measurements on Indium tin oxide thin films (ITO) were performed in the temperature range 14K-400K. This material has low resistivity (~10-4 Ωcm) which raises slightly with increasing temperature, and a high carrier density (η= 4,0 ± 1,1 × 1019 cm-3) which remains almost constant within the whole temperature range. According to the results, ITO can be considered as a degenerated semiconductor with holes acting as majority carriers. Important semiconductor parameters were obtained by simulating the phononic contribution to the resistivity. Keywords: ITO, OLEDs, HOMO, LUMO, electrical resistivity, Hall mobility, Bloch-Grüneisen law, Phonons. © 2009 Revista Colombiana de Física. Todos los derechos reservados. 1. Introducción El óxido de estaño dopado con indio (ITO) es un material ampliamente utilizado en aplicaciones optoelectrónicas debido a la combinación de alta conductividad eléctrica y transparencia óptica. Se usa principalmente para hacer capas conductoras transparentes en pantallas de cristal líquido, en pantallas planas, de plasma, touch panels y tinta electrónica. Su empleo significó una revolución en la industria fotovoltaica, donde se utiliza como ventana óptica. También se usa como detector de gases y en la fabricación de cubiertas anti-estáticas. Fig. 1. Principio de funcionamiento de un OLED. 1 H. Méndez et al.: Mecanismos de transporte eléctrico en películas delgadas de ITO (SnO2:In) Uno de los principales focos de interés del ITO es su aplicación como ánodo o capa inyectora de huecos en diodos orgánicos emisores de luz (OLEDs – organic light emitting diodes). La figura 1 ilustra el uso del ITO como elemento fundamental para la inyección de huecos en la capa orgánica electroluminiscente. El comportamiento rectificador del diodo está determinado por la barrera de inyección, esto es la diferencia energética entre la banda de valencia del ITO (Ev) y la capa de transporte de huecos en el orgánico (HOMO- Highest occupied molecular orbital). De manera análoga existe una barrera de inyección para electrones dada por la diferencia de energías entre la banda de transporte de electrones en la capa orgánica, denominada LUMO (lowest unnocupied molecular orbital) y el nivel de Fermi del metal, barrera que está fuertemente influenciada por la función trabajo del metal. El barrido de temperatura, desde 14K hasta 400K en intervalos de 10K, se efectúo con un criostato Janis CCS400/202 y un control de temperatura Lakeshore 331 que permite una precisión de ±0.1 K con una combinación adecuada de parámetros PID durante la adquisición de datos. Las mediciones para cada temperatura se efectuaron siguiendo el procedimiento recomendado por la compañía Keithley, para eliminar efectos indeseados de la resistencia de contacto, efectos termo-galvanométricos y el voltaje ofsett usual entre las sondas de medición del voltaje Hall [4]. Sin embargo, en vez de tomarse una simple medida de corriente y voltaje, se efectuó un barrido completo de corriente en el intervalo [-1mA, 1mA] en pasos de 0,1 mA para cada temperatura. Esto asegura que la medición de resistividad y movilidad Hall para cada temperatura es el promedio de 40 mediciones. La luminiscencia del dispositivo se presenta por efecto de la recombinación de pares electrón-hueco en el material orgánico electroluminiscente, lo cual da lugar a la emisión de fotones cuya longitud de onda depende de la diferencia entre bandas HOMO-LUMO y de la energía de enlace de los excitones. En otras palabras, el color emitido por el OLED depende en últimas del material orgánico electroluminiscente empleado. 3. Resultados y discusión El espectro de transmisión de las películas de ITO se ilustra en la figura 2, junto con la del sustrato de vidrio sobre el cual se deposita la película delgada. Debido a este principio de funcionamiento resulta esencial la utilización de ITO: un material altamente conductor que sea capaz de inyectar huecos a la capa orgánica y a la vez altamente transparente para permitir que los fotones generados en la capa activa puedan ser emitidos al exterior del dispositivo. Claramente, la eficiencia del dispositivo depende fuertemente de las propiedades eléctricas y ópticas del ITO, las cuales se estudiaron en el presente trabajo. 2. Detalles experimentales Para separar la influencia de las capas que componen la estructura del OLED, en particular las propiedades de los materiales orgánicos, se usó sustratos comerciales de ITO fabricados por la empresa SPI supplies [1]. Para las mediciones de resistividad y movilidad Hall en función de la temperatura se empleó la técnica de Van der Pauw [2,3], usando una muestra cuadrada de ITO en forma de película delgada con 6mm de lado. Las mediciones eléctricas se efectuaron con una fuente de corriente de precisión Keithley 6220 y un nanovoltímetro Keithley 2182, controlados por puerto GPIB para la adquisición de datos con LabView 8.1. Fig. 2. Espectro de transmisión del ITO. La fuerte absorción en el ultravioleta, correspondiente a longitudes de onda menores a los 400 nm es debida a la película de ITO, pues el espectro de transmisión del vidrio presenta un comportamiento aproximadamente constante a 2 rev. col. fís.(c), vol. 41, No. 2, (2009) partir de los 350 nm. La transmisión del ITO en general se encuentra alrededor del 80% sobre todo el espectro visible. Las oscilaciones corresponden a un efecto de interferencia, fuertemente dependiente del espesor de la película. Este efecto puede ser ajustado usando el modelo propuesto por Swannepoel [5]. Como resultado del ajuste se obtiene para el ITO un espesor de 93 nm, valor que se encuentra en el rango de 60nm a 100nm especificado por la compañia [1]. El espesor de la muestra obtenido por este procedimiento, se empleó para la determinación de la resistividad de ITO en función de la temperatura, la cual se observa en la figura 3. Fig. 4. Cálculo de la densidad de huecos en función de la temperatura con base en las mediciones de efecto Hall. Cálculos de primeros principios efectuados recientemente por G. Qin et al. [6] indican que el indio introduce un ligero cambio en la estructura de bandas del SnO2, de tal manera que el máximo de la banda de valencia se eleva aproximadamente 0.3 eV sobre el nivel de Fermi EF en el punto Γ. En consecuencia, los estados vacíos por encima de EF actúan como aceptores de electrones excitados desde la banda de valencia. Es así como se origina el comportamiento metálico de este semiconductor. Fig. 3. Resistividad de ITO en función de la temperatura. De acuerdo con el modelo de conducción metálica de Sommerfeld, la solución a la ecuación de transporte de Boltzmann, usando la función de distribución de FermiDirac, dá lugar a una expresión para la conductividad [7]: 2 (1) e E A muy bajas temperaturas la resistividad se mantiene aproximadamente constante, pero para temperaturas cercanas a 100K se presenta un incremento a medida que aumenta la temperatura. Este comportamiento no es típico de los semiconductores “normales” o no degenerados, y en cambio es más característico de los metales y semiconductores degenerados. Las mediciones de movilidad Hall realizadas sobre la misma muestra (figura 4), confirman que se trata de un semiconductor degenerado con una densidad de portadores casi invariante sobre todo el rango de temperatura, con una densidad de huecos estimada en η = (4,0 ± 1,1) × 1019 cm-3 . De esta forma, el aumento de la resistividad para temperaturas crecientes, indica que hay una dispersión de los portadores por efecto de las vibraciones de la red (fonones). = F mv siendo e la carga elemental, λ(EF) el camino libre medio de los portadores que participan en la conducción (con energía cercana a la energía de Fermi), m la masa efectiva y v la rapidez de los portadores de carga. En esta expresión el único parámetro dependiente de la temperatura es λ(EF). Los electrones son dispersados por fonones y por imperfecciones permanentes en la red como impurezas, vacancias, defectos intersticiales, dislocaciones, fronteras de grano y superficies externas. El término permanente implica 3 H. Méndez et al.: Mecanismos de transporte eléctrico en películas delgadas de ITO (SnO2:In) la línea base de la curva de resistividad, ΘD la temperatura en la que la resistividad comienza a incrementarse y mh* el rango de valores entre los que cambia la resistividad. Esto sugiere que existe una combinación única de estos parámetros para ajustar los datos experimentales. que su contribución a la resistividad eléctrica es independiente de la temperatura. Para la combinación de ambos procesos el camino libre medio toma la forma: (2) 1 1 1 = imp fon En cuanto a la temperatura de Debye, los estudios más aproximados se han efectuado desde el punto de vista teórico sobre SnO2 con base en sus constantes elásticas, dando como resultado 570K [9]. Podría pensarse que la temperatura de Debye deducida para ITO en este trabajo (750K) es excesiva, pero es muy tranquilizador el hecho de que su temperatura de fusión es mayor que 1930K [9]. Podría decirse que no hay un criterio claro para decidir la validez del resultado experimental obtenido en el presente trabajo, pero al menos éste establece un estimativo de su valor aproximado. De esta manera la resistividad tendrá una contribución fonónica y otra debida a imperfecciones, hecho conocido como regla de Mathiesen. (3) mv 1 1 T = e 2 imp fon Para dar cuenta del camino libre medio de portadores afectados por vibraciones de la red, Grüneisen propuso una relación semi-empírica que ha sido probada con gran éxito en muchos metales, expresión que en la física del estado sólido se denomina como ley de Bloch-Grüneisen, la cual describe la interacción entre electrón y fonones acústicos: (4) 1 x5⋅dx 5 /T fon =CT ∫ D 0 Al parecer no existen estudios para determinar experimentalmente la masa efectiva para huecos (mh*) en ITO. El estudio más exhaustivo para ITO con estructura tipo rutilo fué efectuado teóricamente por el grupo de Quin [6]. Con base en la curvatura de las bandas, predice cualitativamente que la masa efectiva para huecos es mayor que la del electrón. e x −11−e− x donde ΘD es la temperatura de Debye, T es la temperatura medida y C una constante. Esta integral no tiene solución analítica. Sin embargo, se han realizado algunos intentos exitosos de aproximar esta integral y obtener una expresión analítica en términos de una serie de potencias [8]. Bajo esta aproximación y con base en el valor para la densidad de portadores η obtenida experimentalmente, se efectuó el ajuste de las mediciones de resistividad en función de la temperatura, usando la ecuación (3). Los resultados del ajuste mostrado en la figura 3 se resumen en la tabla 1. Una manera alternativa de estimar mh* consistiría en hacer una comparación con el caso de SnO2 puro, y suponer que el dopaje con indio no altera significativamente su estructura cristalina. Cálculos desde primeros principios efectuados por F. El Haj Hassan et al. [10], para SnO2 con una estructura de tipo rutilo, usando la aproximación de gradiente generalizado (GGA) y Engel-Vosko GGA respectivamente, dan como resultado valores teóricos de 0,602m0 y 0,682m0, en muy buen acuerdo con el presente resultado experimental. Tabla No. 1 Parámetros físicos usados para ajustar la curva de resistividad en función de la temperatura. η (cm-3) EF (eV) v mh*/m0 (cm / s) 4×1019 4,28 1,2×108 0,61 ΘD (K) λimp ( cm ) 750 0,76 Conclusiones Las mediciones de propiedades eléctricas en función de la temperatura permitieron determinar experimentalmente importantes parámetros del semiconductor degenerado SnO2:In, mediante un modelo en el que se tiene en cuenta que el mecanismo de dispersión dominante es la interacción electrón-fonón. Estos valores deben ser confirmados teórica y/o experimentalmente por mediciones independientes adicionales. Las propiedades de transporte del ITO obtenidas en este estudio, se van a emplear para el posterior La energía de Fermi y la velocidad de los portadores se calcularon asumiendo que los portadores de carga pertenecen a un gas fermiónico. La masa efectiva de los huecos, la temperatura de Debye y el camino libre medio asociado a imperfecciones del material son resultado del mejor ajuste obtenido entre el modelo y los datos experimentales de resistividad. En particular, λimp determina 4 rev. col. fís.(c), vol. 41, No. 2, (2009) modelamiento de la respuesta de eléctrica de dispositivos como OLEDs, en los que el ITO actúa como electrodo inyector de huecos a la capa orgánica electroluminiscente. Agradecimientos: Este trabajo fué el resultado de la ejecución del proyecto 001820 financiado por la Vicerrectoria Académica de la Pontificia Universidad Javeriana. Referencias [1] SPI supplies, Página oficial de la compañía. [en línea]. <http://www.2spi.com/catalog/standards/ITO-coated-coverslips.shtml> [citado el 30 de septiembre de 2009] [2] Van der Pauw, L.J. A method of measuring specific resistivity and Hall effect of discs of arbitrary shape. En: Philips Research Reports. No 13 (1958); p. 1–9. ISSN 00317918 . [3] National Institut of Standards and Technology, Página oficial. [En línea] <http://www.eeel.nist.gov/812/hall.html> [citado el 30 de septiembre de 2009]. [4] Keithley instruments, página oficial de la compañía. [en línea] <http://www.keithley.com/data?asset=15222> [Citado el 30 de septiembre de 2009]. [5] R. Swanepoel. Determination of the thickness and optical constants of amorphous silicon. En: J. Phys. E.: Sci. Instrum. No 16 (1983) p.1214-1222. ISSN 0022-3735. [6] G. Qin, D. Li, Z. Feng y S. Liu. First principles study on the properties of p-type conducting In:SnO 2. En: Thin solid films Vol 17 (2009); p. 3345-3349. ISSN: 0040-6090. [7] J. S. Blakemore. Solid state physics. 1st Edition. Boca ratón (FL): W. B. Saunders company, 1969. p.170. Serie 98765832. ISBN: 10: 0521313910. [8] M. Deutsch. An accurate analytical representation for the Bloch-Grüneisen integral. En: J. Phys. A: Math. Gen. No 20 (1987); p. L811-L813. ISSN: 1751-8113. [9] O. Madelung, V. Rössler and M. Schulz. Non-Tetrahedrally bonded elements and binary compounds I. Vol 41C. Serie Landolt-Börnstein – Group III – Condensed Matter numerical data and functional relationship in science and technology. Springer Verlag (1998). ISBN: 978-3-54064583-2. ISSN: 1615-1925. [10] F. El Haj Hassan, A. Alaeddine, M. Zoaeter and I. Rachidi. First principles investigation of SnO2. En: International Journal of Modern Physics B. Vol. 19, No. 27 (2005); p. 4081-4092. ISSN: 0217-9792. 5