P 5.8

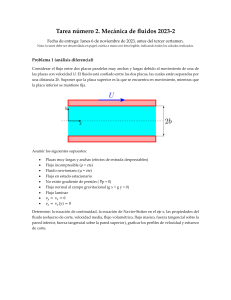
Mecánica de fluidos
GEVA: Aleix Gimeno
Alèxia Jou
Enrique López
Problema 5.8.
Un depósito contiene un cierto fluido de viscosidad μ y densidad ρ.
Paea extraer el fluido usamos dos cintas transportadoras verticales de ancho
D y longitud L y separadas una distancia h, mucho menor que el ancho y la
longitud de las cintas.
Si las cintas de mueven con una velocidad vertical hacia arriba V, y
suponiendo que la viscosidad del fluido es lo suficientemente grande como
para que el flujo pueda ser considerado laminar, calcular:
1. el caudal del fluido extraido
2. la fuerza que deben hacer las cintas debida a la fricción del fluido.
Hipotesis:
1.
2.
3.
4.
5.
Flujo incompresible
Flujo bidimensional ( D y L>>h)
Flujo laminar
Régimen estacionario
despreciable
1.
es nulo ya que es flujo bidimensional.
es nulo ya que supusimos flujo laminar, y por lo tanto, no hay velocidad en el eje
x.
es nulo por que es incompresible, con lo que llegamos a la conclusión que v solo
depende del eje x.
Como v=0 y
la ecuación queda de tal manera:
Obtenida la ecuación diferencial, solo hará falta integrar:
 dv  g
d  
dx
 dx  
 g

dv   x  C1  dx


Volvemos a integrar para obtener el perfil de velocidades:
v
g 2
x  C1 x  C 2
2
Imponemos las condiciones de contorno, en que la velocidad del fluido será igual a
la velocidad de las paredes V. De esta forma obtendremos las constantes C1 i C2 .
x
→ v V → V  C2
↓
x h→v V → V 
g 2
g
h  C1 h  V → C1  
h
2
2
Por tanto, el perfil de velocidades de nuestro probema es:
v( x) 
g 2 g
x 
hx  V
2
2
Par obtener el caudal aplicaremos que Q   vdS
s
Así, tenemos que:
h
h  g


g
gh 3 

Q  D  v( x)dx D  
x2 
hx  V dx  D hV 
0
0 2
2
12





2.Tenemos que calcular el esfuerzo cortante y evaluarlo en la posición de las cintas.
Con el esfuerzo cortante podremos encontrar la fuerza que deben ejercer éstas.
Debemos tener en cuenta que hay dos cintas, por lo tanto encontramos la fuerza
que ejerce una y lo multiplicamos por dos.
 1

 

v
2

x
gx 2 
gh 
x 
2  
x
gx gh 
gh
  

 gx 
2 
2
 
F   * S  2* DL  2DL*  x h




gh 
F  2DLgh 
 DLgh

2 