Cálculo de distancias
Anuncio
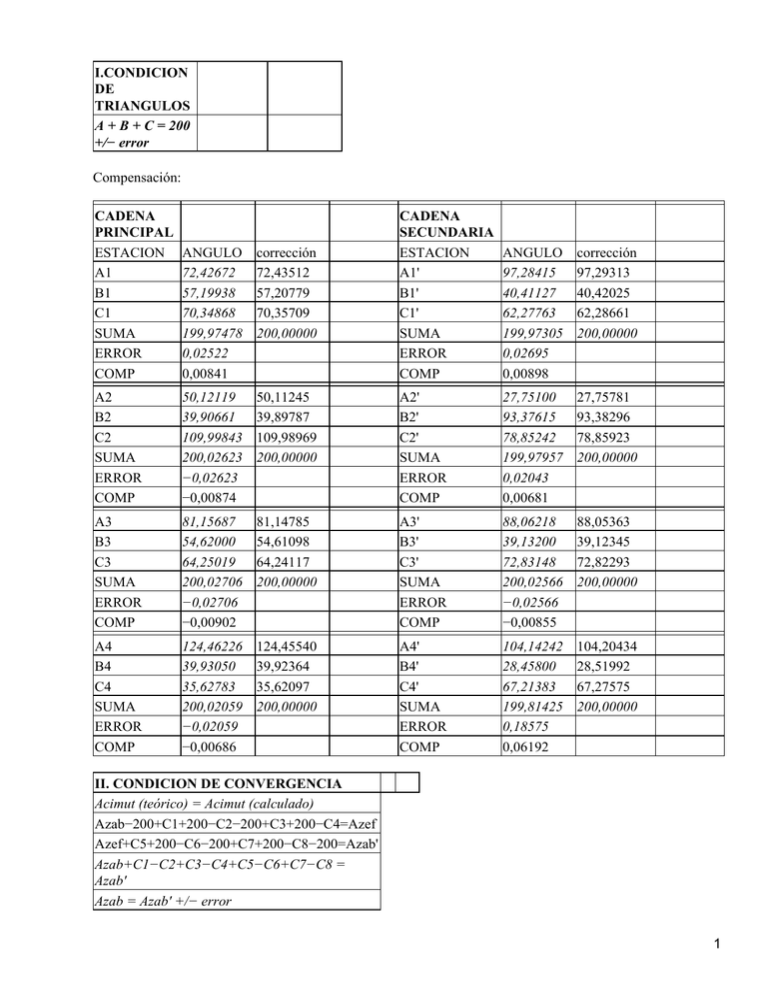
I.CONDICION DE TRIANGULOS A + B + C = 200 +/− error Compensación: CADENA PRINCIPAL ESTACION A1 B1 C1 SUMA ERROR COMP CADENA SECUNDARIA ESTACION A1' B1' C1' SUMA ERROR COMP ANGULO 72,42672 57,19938 70,34868 199,97478 0,02522 0,00841 corrección 72,43512 57,20779 70,35709 200,00000 ANGULO 97,28415 40,41127 62,27763 199,97305 0,02695 0,00898 corrección 97,29313 40,42025 62,28661 200,00000 A2 B2 C2 SUMA ERROR COMP 50,12119 39,90661 109,99843 200,02623 −0,02623 −0,00874 50,11245 39,89787 109,98969 200,00000 A2' B2' C2' SUMA ERROR COMP 27,75100 93,37615 78,85242 199,97957 0,02043 0,00681 27,75781 93,38296 78,85923 200,00000 A3 B3 C3 SUMA ERROR COMP 81,15687 54,62000 64,25019 200,02706 −0,02706 −0,00902 81,14785 54,61098 64,24117 200,00000 A3' B3' C3' SUMA ERROR COMP 88,06218 39,13200 72,83148 200,02566 −0,02566 −0,00855 88,05363 39,12345 72,82293 200,00000 A4 B4 C4 SUMA ERROR COMP 124,46226 39,93050 35,62783 200,02059 −0,02059 −0,00686 124,45540 39,92364 35,62097 200,00000 A4' B4' C4' SUMA ERROR COMP 104,14242 28,45800 67,21383 199,81425 0,18575 0,06192 104,20434 28,51992 67,27575 200,00000 II. CONDICION DE CONVERGENCIA Acimut (teórico) = Acimut (calculado) Azab−200+C1+200−C2−200+C3+200−C4=Azef Azef+C5+200−C6−200+C7+200−C8−200=Azab' Azab+C1−C2+C3−C4+C5−C6+C7−C8 = Azab' Azab = Azab' +/− error 1 Azab = 117.43788 Azab' = 117.45092 Error = −0.01304 Compensación C = −0.001630312 Compensación A y B = 0.000815156 TRIANGULO A 1 72,43594 2 50,11326 3 81,14866 4 124,45621 5 28,52073 6 39,12426 7 93,38378 8 40,42107 B 57,20860 39,89868 54,61179 39,92445 104,20515 88,05444 27,75863 97,29395 C 70,35546 109,98805 64,23954 35,61934 67,27412 72,82130 78,85760 62,28498 SUMA 200,00000 200,00000 200,00000 200,00000 200,00000 200,00000 200,00000 200,00000 III. CONDICIÓN DE LADOS L2 = ][ sen A L1 ][ sen B TRIANGULO 1 2 3 4 5 6 7 8 Sen A¡ 0,90772144 0,70836369 0,95647706 0,9271146 0,43316612 0,5766011 0,99460441 0,5931233 ][ Sen A¡ ][ Sen B¡ ][ Sen A¡ = 0,084012164 = 0,084265705 Sen B¡ 0,78247497 0,58649697 0,75643157 0,58682478 0,9978192 0,98244713 0,42234558 0,99909673 Cotg A¡ 0,46222699 0,99644808 0,30508577 −0,4042412 2,08075853 1,41696886 0,10430321 1,35741024 Cotg B¡ 0,79578526 1,38099847 0,86468209 1,37982236 −0,0661506 0,18987406 2,14619243 0,04253218 = 0,996991178 ][ Sen B¡ Suma CotgA¡ Suma CotgB¡ = 6,31896045 = 6,73373624 Xc = 146,9634774 0,014696348 Primera Compensación 2 TRIANGULO 1 2 3 4 5 6 7 8 A 72,45064 50,12796 81,16336 124,47091 28,53543 39,13896 93,39847 40,43576 B 57,19391 39,88399 54,59710 39,90976 104,19046 88,03975 27,74393 97,27925 C 70,35546 109,98805 64,23954 35,61934 67,27412 72,82130 78,85760 62,28498 SUMA 200,00000 200,00000 200,00000 200,00000 200,00000 200,00000 200,00000 200,00000 TRIANGULO 1 2 3 4 5 6 7 8 Sen A 0,90781827 0,70852661 0,95654439 0,92702806 0,43337418 0,5767897 0,99462833 0,59330914 Sen B 0,7823312 0,58630998 0,75628056 0,58663784 0,99783441 0,98240405 0,42213632 0,9990869 Cotg A 0,46194685 0,99598813 0,30483345 −0,4045098 2,07952879 1,41627474 0,10406986 1,35675424 Cotg B 0,79616237 1,3816698 0,86508563 1,38049294 −0,0659188 0,19011324 2,14748725 0,04276345 ][ Sen A¡ ][ Sen B¡ ][ Sen A¡ = 0,084134765 = 0,084134777 = 0,999999859 ][ Sen B¡ Suma CotgA¡ Suma CotgB¡ = 6,31488622 = 6,73785592 Xc 0,006896078 6,89608E−07 Segunda TRIANGULO 1 2 3 4 5 6 7 8 Compensación A 72,45064 50,12796 81,16336 124,47091 28,53543 39,13896 93,39847 40,43577 B 57,19391 39,88399 54,59710 39,90976 104,19045 88,03974 27,74393 97,27925 C 70,35546 109,98805 64,23954 35,61934 67,27412 72,82130 78,85760 62,28498 SUMA 200,00000 200,00000 200,00000 200,00000 200,00000 200,00000 200,00000 200,00000 TRIANGULO 1 2 3 Sen A 0,90781827 0,70852662 0,9565444 Sen B 0,78233119 0,58630997 0,75628055 Cotg A 0,46194684 0,9959881 0,30483344 Cotg B 0,79616239 1,38166984 0,86508564 3 4 5 6 7 8 0,92702806 0,43337419 0,57678971 0,99462833 0,59330915 ][ Sen A¡ ][ Sen B¡ ][ Sen A¡ = 0,084134771 = 0,084134771 0,58663783 0,99783441 0,98240404 0,42213631 0,9990869 −0,4045098 2,07952874 1,41627471 0,10406984 1,35675421 1,38049297 −0,0659187 0,19011325 2,14748731 0,04276346 =1 ][ Sen B¡ SuCotgA¡ SuCotgB¡ = 6,31488603 = 6,73785611 Xc =0 Triángulos 1 2 3 4 5 6 7 8 Angulos Horizontales A' 72,45064 50,12796 81,16336 124,47091 28,53543 39,13896 93,39847 40,43577 B' 57,19391 39,88399 54,59710 39,90976 104,19045 88,03974 27,74393 97,27925 Medición de la Base Desde A a B A 1 delta 1 2 delta 2 3 delta 3 B delta C' 70,35546 109,98805 64,23954 35,61934 67,27412 72,82130 78,85760 62,28498 SUMA 200,00000 200,00000 200,00000 200,00000 200,00000 200,00000 200,00000 200,00000 Desde B a A anotación 0,2 20,15 0,012 0,2 20,1 −0,018 0,2 19,65 −0,026 0,2 15,9 0,023 suma distancia A−1 19,95 0,012 12 19,9 −0,018 23 19,45 −0,026 3−B 15,7 0,023 74,991 B 3 delta 3 2 delta 2 1 delta 1 A delta A−B anotación 0,2 15,9 0,036 0,2 19,6 0,039 0,2 20,05 −0,026 0,2 20,2 −0,005 suma distancia A−1 15,7 0,036 12 19,4 0,039 23 19,85 −0,026 3−B 20 −0,005 74,994 4 Distancia A−B 74,9941 74,9925 Base Compensación de la base Corrección temperatura:. 0,0082912 por Corrección tensión: 0,00314062 por Corrección tarjeta: −0,009 por Reducción al Horizonte: 0,00076 Distancia 74,9925 A−B Distancia Compensada 74,99417182 CALCULO DE DISTANCIAS Por teorema del seno Cadena Primaria Angulos Triángulo 1 2 3 4 Lados Triángulo 1 2 3 4 Cadena Angulos Triángulo 1' 2' 3' 4' Lados Triángulo 1' Sen Sen Sen C' A'B' 0,907818275 0,782331193 0,89352748 0,708526621 0,586309969 0,987717675 0,956544398 0,756280553 0,846338098 0,927028056 0,586637832 0,530768637 a¡b¡c¡ 87,02326472 74,9941 85,65335221 105,1633145 87,02326472 146,6023457 133,0106651 105,1633145 117,6861143 210,1886574 133,0106651 120,3432263 Secundaria Sen Sen Sen C' A'B' 0,999086896 0,593309151 0,829588447 0,42213631 0,994628328 0,945358448 0,982404043 0,576789706 0,910244538 0,997834415 0,433374188 0,870756806 a¡' b¡'c¡' 126,284286 74,9941 104,8597325 5 2' 3' 4' 53,59708844 126,284286 120,0286712 91,28803073 53,59708844 84,58274566 210,1886574 91,28803073 183,4204166 CALCULO DE COORDENADAS MEDIANTE POLIGONAL Primera Cadena Sea la Primera Cadena una Poligonal Cerrada ACEFDB Acimut (AB) AZIMUTES AC CE EF FD DB BA CERRADA 117,43788 forma Valor Az (AB) 44,98724 − A Az (AC) + 396,64192 200 − C Az (CE) + 106,42549 200 − E Az (EF) + 266,51573 200 − F Az (FD) + 237,92130 200 − D Az 317,43788 (DB) +200 − Angulo Forma Valor A A = 72,45064 A1 C C = B1 + 248,34532 C2 + A3 E E = B3 90,21643 + C4 F F = 39,90976 B4 D B D = A4 + 228,59443 C3 + B2 B 120,48342 = A2 + 6 B AC Distancia c1 = AC c3 = CE a4 = EF c4 = FD c2 = DB b1 = BA Az (BA) +200 44,98724 − A N=6 C1 ( N − 2800800,00000 )* 200 = DEstación NORTE ESTE 85,65335221 A6457930,32 405280,72 117,6861143 C 6457995,462 405336,3343 210,1886574 E 6458112,985 405330,1295 120,3432263 F 6458091,806 405539,2484 146,6023457 D6458031,388 405435,1711 74,9941 B 6457910,034 405352,9183 A6457930,32 405280,72 SEGUNDA CADENA Sea la Primera Cadena una Poligonal Cerrada AC'EFD'B Acimut (AB) AZIMUTES AC' C'E EF FD' = 117,43788 forma Valor Az (AB) 20,15863 − A Az (AC') + 12,82552 200 − C' Az (C'E) + 106,41244 200 − E Az 277,87701 (EF) + 200 − Angulo Forma Valor A A = 97,27925 A1' C' C' = B1' + 207,33311 C2' + A3' E E = B3' 106,41308 + C4' F F 28,53543 = B4' 7 F D'B Az (FD') + 207,46679 200 − D' D' BA Az (D'B) +200 317,43788 − B B AC' Az (BA) +200 20,15863 − A N=6 Distancia c1' = AC' c3' = C'E a4' = EF c4' = FD' c2' = D'B b1' = BA D' = A4' + 270,41022 C3' + B2' B = A2' 90,02891 + C1' ( N − =800 800,00000 2 )* 200 DEstación NORTE ESTE 104,8597325 A6457930,32 405280,72 84,58274566 C'6458029,966 405313,3718 210,1886574 E 6458112,839 405330,2971 183,4204166 F 6458091,703 405539,4204 120,0286712 D'6458029,238 405366,964 74,9941 B 6457910,034 405352,9183 A6457930,32 405280,72 Calculo de Rigidez Primera Cadena Angulos A¡ Sen ( A¡ + 1" ) 0,907818934 0,708527729 0,956544856 0,927027467 Log (Sen A¡ Log(Sen dA¡ ) A¡+1) −0,04200108 −0,04200076 −0,31513402 −0,14964383 −0,14964315 −0,679450241 −0,01929487 −0,01929466 −0,207953183 −0,03290712 −0,0329074 0,275952458 Sen ( B¡ + 1" ) 0,782331193 0,782332171 0,586309969 0,586311241 Log (Sen B¡ Log(Sen dB¡ ) B¡−1) −0,10660935 −0,10660881 −0,543131691 −0,23187272 −0,23187178 −0,942557268 Triangulo Angulo A¡ Sen A¡ 1 2 3 4 72,45064 50,12796 81,16336 124,47091 0,907818275 0,708526621 0,956544398 0,927028056 Triangulo Angulo B¡ Sen B¡ 1 2 57,19391 39,88399 Primera Cadena Angulos B¡ 8 3 4 54,59710 39,90976 0,756280553 0,756281581 −0,12131707 −0,12131648 −0,590150262 0,586637832 0,586639104 −0,23162993 −0,23162899 −0,941754424 Triangulo 1 2 3 4 dA² 0,099309451 0,46165263 0,043244527 0,076149759 dAB dB² 0,171159273 0,294992034 0,640420763 0,888414203 0,122723626 0,348277331 −0,25987945 0,886901395 f ( Aj , Bj ) ð R 0,565460758 3,773365543 2,830024157 1,990487596 0,514245484 0,703171706 Segunda Cadena Angulos A'¡ Triangulo Angulo A'¡ Sen A¡' 1' 2' 3' 4' 97,27925 27,74393 88,03974 104,19045 0,999086896 0,42213631 0,982404043 0,997834415 Sen ( A¡' + 1" ) 0,999086963 0,422137734 0,982404337 0,997834312 Log (Sen Log(Sen dA¡' A¡' ) A¡'+1) −0,00039674 −0,00039671 −0,029172188 −0,37454729 −0,37454583 −1,464987447 −0,00770986 −0,00770973 −0,129692457 −0,00094152 −0,00094157 0,044969523 Sen ( B¡' + 1" ) 0,593310416 0,994628491 0,576790989 0,433375604 Log (Sen B¡' Log(Sen dB¡' ) B¡'−1) −0,22671895 −0,22671803 −0,92556016 −0,00233918 −0,0023391 −0,070994676 −0,2389825 −0,23898153 −0,966164249 −0,36313696 −0,36313554 −1,418627065 Segunda Cadena Angulos B¡' Triangulo Angulo B¡' Sen B¡' 1' 2' 3' 4' 40,43577 93,39847 39,13896 28,53543 0,593309151 0,994628328 0,576789706 0,433374188 Triangulo 1' 2' 3' 4' dA'² 0,000851017 2,14618822 0,016820133 0,002022258 dA'B' dB'² 0,027000615 0,856661609 0,104006309 0,005040244 0,125304215 0,933473355 −0,06379498 2,012502748 f ( A'j , B'j ) ð R' 0,884513241 6,16607574 4,624556805 2,255234773 1,075597704 1,950730023 Calculo de Cotas Aplicando lo siguiente Camino AB ===> CB = CA + Hi(a) − Hj(b) + Dab / Tg(Vab) Camino BA ===> CB = CA − Hi(b) + Hj(a) − 9 Dba / Tg(vba) Como en todos los casos la Hj es cero, no se ocupará Distancia xy c1 = AC c3 = CE a4 = EF c4 = FD c2 = DB b1 = BA D Estación 85,65335221 A 117,6861143 C 210,1886574 E 120,3432263 F 146,6023457 D 74,9941 B A Camino escogido AC − EC − FE − FD − DB − BA EST A C E F D B A' error Distancia xy c1 = AC' c3 = C'E a4 = EF c4 = FD' c2 = D'B b1 = BA Camino escogido Hi V ( xy ) V ( yx ) Tg[V(xy)] Tg[V(yx)] 1,51 1,52 1,3 1,32 1,21 1,62 93,88910 86,78970 93,44300 116,75300 109,90960 100,22430 107,03730 114,74700 104,90700 84,41200 95,53720 98,11420 10,38576 4,74975 9,67465 −3,71191 −6,37230 −283,82396 −9,00949 −4,23945 −12,94800 4,00209 14,24166 33,74873 Compensacion Comp = error x est(acum) / est (Total) COTA 457,19000 466,94719 493,40694 508,32023 477,21938 455,42320 456,77897 0,41103 Comp Cota Comp 0 457,19000 0,068504834 467,01570 0,137009668 493,54395 0,205514502 508,52574 0,274019336 477,49340 0,34252417 455,76572 0,411029003 457,19000 D Estación 104,8597325 A 84,58274566 C' 210,1886574 E 183,4204166 F 120,0286712 D' 74,9941 B A Hi V ( xy ) V ( yx ) Tg[V(xy)] Tg[V(yx)] 1,51 1,47 1,3 1,32 1,36 1,62 92,71430 83,97820 93,44300 112,82700 109,45700 100,22430 108,24210 117,38900 104,90700 87,91110 95,92640 98,11420 8,69975 3,88921 9,67465 −4,89578 −6,68214 −283,82396 −7,68080 −3,56954 −12,94800 5,20270 15,60661 33,74873 Compensacion 10 AC' − C'E − FE − D'F − DB − BA EST A C' E F D' B A' error Comp = error x est(acum) / est (Total) COTA 457,19000 470,75318 493,97122 508,88450 472,26966 455,66706 457,28135 −0,09135 Comp Cota Comp 0 457,19000 −0,01522456 470,73796 −0,03044912 493,94077 −0,04567369 508,83883 −0,06089825 472,20876 −0,07612281 455,59093 −0,09134737 457,19000 Cota Comp 457,19000 467,01570 493,54395 508,52574 477,49340 455,76572 457,19000 PROMEDIOS Est COTA A 457,19000 C 467,01570 C' 470,73796 D 477,49340 D' 472,20876 E 493,74236 F 508,68229 B 455,67833 11