R_3.
Anuncio
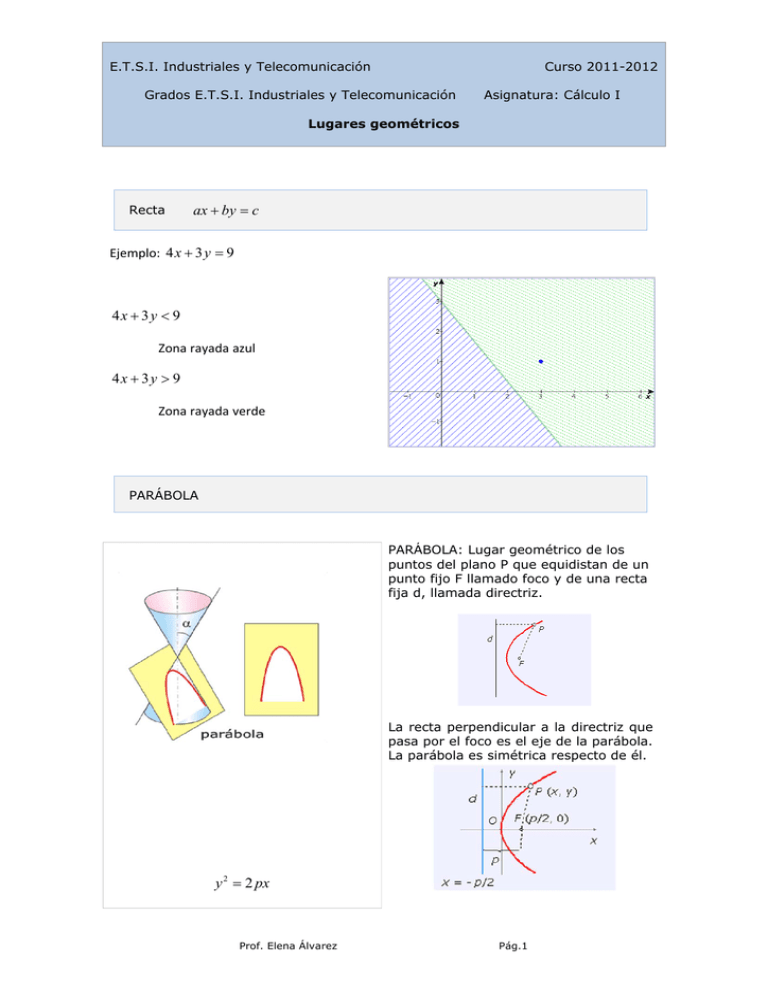
E.T.S.I. Industriales y Telecomunicación Curso 2011-2012 Grados E.T.S.I. Industriales y Telecomunicación Asignatura: Cálculo I Lugares geométricos Recta ax by c Ejemplo: 4 x 3 y 9 4 x 3 y 9 Zona rayada azul 4 x 3 y 9 Zona rayada verde PARÁBOLA PARÁBOLA: Lugar geométrico de los puntos del plano P que equidistan de un punto fijo F llamado foco y de una recta fija d, llamada directriz. La recta perpendicular a la directriz que pasa por el foco es el eje de la parábola. La parábola es simétrica respecto de él. y 2 2 px Prof. Elena Álvarez Pág.1 E.T.S.I. Industriales y Telecomunicación Curso 2011-2012 Grados E.T.S.I. Industriales y Telecomunicación Asignatura: Cálculo I Lugares geométricos CIRCUNFERENCIA CIRCUNFERENCIA: Lugar geométrico de los puntos del plano P que equidistan de un punto fijo C llamado centro. d P, C r Ecuación reducida: x a y b 2 2 r Ejemplo: x 3 y 1 2 2 4 x 3 y 1 2 2 4 Zona rayada azul x 3 y 1 2 2 4 Zona rayada verde Prof. Elena Álvarez Pág.2 E.T.S.I. Industriales y Telecomunicación Curso 2011-2012 Grados E.T.S.I. Industriales y Telecomunicación Asignatura: Cálculo I Lugares geométricos ELIPSE ELIPSE: Lugar geométrico de puntos del plano cuya suma a dos puntos fijos llamados fijos es constante (2a). d P, F d P, F ' cte 2a Ecuación reducida: x c1 2 a2 y c2 2 b2 1 a 2 b 2 c 2 (c distancia focal) c Excentricidad: e a Ejemplo: x 3 22 2 y 1 42 2 1 x 3 2 22 y 1 2 1 42 Zona rayada azul x 3 22 2 y 1 42 2 1 Zona rayada verde Prof. Elena Álvarez Pág.3 E.T.S.I. Industriales y Telecomunicación Curso 2011-2012 Grados E.T.S.I. Industriales y Telecomunicación Asignatura: Cálculo I Lugares geométricos HIPÉRBOLA: Lugar geométrico de los puntos del plano cuya diferencia en valor absoluto a dos puntos fijos llamados focos es constante (2a). d P, F d P, F ' cte 2a Ecuación reducida: x c1 2 a2 y c2 2 b2 1 a 2 b2 c2 Excentricidad: e x 3 Ejemplo: 2 22 y 1 42 2 1 x 3 2 22 y 1 2 y 1 2 1 Zona rayada azul 42 x 3 22 2 42 1 Zona rayada verde Prof. Elena Álvarez Pág.4 c a