PIU SABATINO SERIE IV MATEMÁTICAS COORDINACIÓN
Anuncio

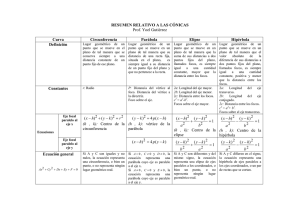
PIU SABATINO SERIE IV MATEMÁTICAS COORDINACIÓN DE MATEMÁTICAS, FÍSICA, ESTADÍSTICA E INFÓRMATICA El círculo se define como: a) Una figura regular. b) El lugar geométrico de los puntos que equidistan de un punto fijo llamado centro. c) Una figura con un punto llamado centro. d) Una figura con una tangente. 2.- La ecuación del círculo cuyo diámetro son los puntos (-3/4, - ¾) y (¾ , ¾) es: a) 𝑥 2 + 𝑦 2 = 2 2 −9 8 9 b) 𝑥 + 𝑦 = 8 9 c) 𝑥 2 − 𝑦 2 = 8 d) −𝑥 2 + 𝑦 2 = 9 8 3.- La ecuación de la circunferencia que pasa por (1,-4) y que es concéntrica con 𝑥 2 + 𝑦 2 – x + 10y + 18 = 0. a) b) c) d) 𝑥2 𝑥2 𝑥2 𝑥2 + 𝑦2 + 𝑦2 + 𝑦2 + 𝑦2 – x + 10y + 24 = 0. – x - 10y - 24 = 0. + x + 10y + 24 = 0. – x + 10y - 24 = 0. 4.- El centro y radio del círculo 4𝑥 2 + 4𝑦 2 + 12 x - 12y + 14 = 0, son: a) b) c) d) C ( -3/2, 3/2) y r = -1 C ( -3/2, -3/2) y r = 1 C ( -3/2, 3/2) y r = 1 C ( 3/2, 3/2) y r = 1 5.- El centro y radio del círculo 𝑥 2 + 𝑦 2 + 4 x - 2y + 2 = 0, son: a) b) c) d) C(-2,-1) y r = √3 C(-2,1) y r =- √3 C(2,1) y r = √3 C(-2,1) y r = √3 6.- La parábola se define como: a) El lugar geométrico de los puntos del plano que equidistan de una recta fija y de un punto fijo que no está en dicha recta. b) Una figura regular. c) Una figura con vértice d) Una figura con un punto fijo llamado foco. 7.- La ecuación de la parábola con vértice en el origen y directriz y = -2 es: a) b) c) d) 𝑥 2 = - 8y 𝑥 2 = 8y −𝑥 2 = 8y 𝑦 2 = - 8x 8.- El foco y la directriz de la parábola 𝑦 2 − 24𝑥 = 0 son: a) b) c) d) F(6,0) F(-6,0) F(6,0) F(-6,0) D:x=6 D:x=-6 D:x=-6 D:x= 6 9.- EL foco y vértice de la parábola y² + 10y – 24x + 49 = 0, son: a) b) c) d) F(-7,-5) F(-7,5) F(7,-5) F(7,-5) V(-1,-5) V(-1,-5) V(-1,5) V(1,-5) 10.- La ecuación de la recta tangente a la parábola 3y² + 6y – 4x – 5 = 0, en el punto (10,3) es: a) b) c) d) y = 1/6 x + 4/3 y = 1/6 x - 4/3 y = -1/6 x + 4/3 y = -1/6 x - 4/3 11.- La elipse se define como: a) una figura irregular b) el lugar geométrico de los puntos del plano cuya suma de distancias a dos puntos fijos es constante c) una figura regular con vértices d) el lugar geométrico de los puntos del plano cuyas distancias a dos puntos fijos tienen una diferencia constante 12.- La ecuación de la elipse con focos (0,25);(0,-25) y vértices (0,30);(0,-30) es: a) b) 𝑥2 𝑦2 𝑥2 900 𝑦2 + 275 − =1 275 𝑥2 900 𝑦2 𝑥2 𝑦2 c) − 275 + d) =1 275 + 900 900 =1 = −1 13.- El centro y los focos de la elipse 4x² + y² + 64x – 6y + 201 = 0, son: a) b) c) d) C(-8,-3) C(8,3) C(-8,3) C(8,-3) F(-8, -3 + 4√3) F’ ( - 8 , -3 - 4√3) F(-8, 3 + 4√3) F’ ( - 8 , 3 - 4√3) F(-8, 3 + 4√3) F’ ( - 8 , 3 - 4√3) F(8, -3 + 4√3) F’ ( 8 , -3 - 4√3) 14.- La ecuación de la elipse con vértices (4,0), (-4,0) y que pasa por el punto (0,3) es: a) b) c) d) 𝑥² 9 𝑥² 16 𝑥² 9 𝑥² 16 + + + + 𝑦² 16 𝑦² 16 𝑦² 9 𝑦² 9 =1 =1 =1 =1 15.- Los puntos de intersección de las elipses 16x² + 25y² - 400 = 0 y 16x² + y² 16 = 0, son: a) b) c) d) (0,4) y (0, -4) (0,5) y (0, -5) (0,4) y (0, 4) (0,5) y (0,5) 16.- La hipérbola se define como: a) el lugar geométrico de los puntos del plano cuyas distancias a dos puntos fijos tienen una diferencia constante b) una figura regular con vértices y centro c) el lugar geométrico de los puntos del plano cuya suma de distancias a dos puntos fijos es constante d) una figura regular con directriz. 17.- Los vértices y los focos de la hipérbola -9x² + 4y² - 36 = 0, son: a) b) c) d) V(0,3) V(0,3) V(0,3) V(0,3) V’(0,-3) V’(0,-3) V’(0,-3) V’(0,-3) y y y y F(0, √12) F(0, √13) F(0, √14) F(0, √15) F’(0, - √12) F’(0, - √13) F’(0, - √14) F’(0, - √15) 18.- La ecuación de la hipérbola con focos (-5,0);(5,0) y la distancia entre sus vértices mide 4, es: a) b) c) d) 𝑥² 4 𝑥² 21 𝑥² 4 𝑥² 21 − − − − 𝑦² 4 𝑦² 4 𝑦² 21 𝑦² 21 =1 =1 =1 =1 19.- Las coordenadas de los vértices y las ecuaciones de las asíntotas de la hipérbola x² - y² - 4x – 4y – 400 = 0, son: a) b) c) d) V( 22, -2) V( 22, -2) V( 22, -2) V( 22, -2) V’(-18,-2) V’(-18,-2) V’(-18,-2) V’(-18,-2) y=x–4 y=x y=x–4 y= -x y=x+4 y= -x y=-x–4 y=x 20.- La ecuación de la recta tangente a la hipérbola -x² + 2y² - 20y + 48 = 0 en el punto (4,8) es: a) b) c) d) 2x – 3y + 16 = 0 2x – 3y - 16 = 0 2x + 3y + 16 = 0 2x + 3y - 16 = 0