Tema 3
Anuncio

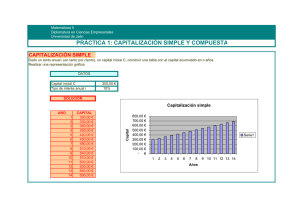
Facultad de CC.EE. – Dpto. de Economía Financiera I Diapositiva 1 Matemática Financiera TEMA 3 SISTEMAS FINANCIEROS 1. Sistemas financieros. Tipología 2. Capitalización Simple. Propiedades e interpretación 3. 4. 5. 6. 7. financiera Capitalización Compuesta. Propiedades. Tanto efectivo y tanto nominal Descuento simple comercial Descuento compuesto Comparación entre Capitalización Simple y Compuesta. Comparación entre Descuento Simple Comercial y Compuesto Facultad de CC.EE. – Dpto. de Economía Financiera I Diapositiva 2 Matemática Financiera. Tema 3 – Sistemas financieros 1. Sistemas financieros. Tipología - Sistemas Estacionarios . Los resultados que se obtienen al utilizar distintas leyes de un sistema estacionario dependen sólo de la amplitud del intervalo de aplicación y no de donde esté situado el origen del tiempo L(t ; p) = L(t + h ; p + h) ∀h L(t ; p ) = L( z ) siendo z = p − t > 0 - Sistemas Sumativos Los resultados de la aplicación sucesiva de leyes de un sistema sumativo se acumulan en forma de suma. La suma de los intereses acumulados correspondientes a dos intervalos consecutivos es igual a la cuantía del interés acumulado correspondiente al intervalo total. I (t ; s ) + I ( s ; p ) = I (t ; p ) [L(t ; s) − 1] + [L( s ; p) − 1] = [L(t ; p) − 1] Facultad de CC.EE. – Dpto. de Economía Financiera I Diapositiva 3 Matemática Financiera. Tema 3 – Sistemas financieros 1. Sistemas financieros. Tipología - Sistemas Multiplicativos La aplicación sucesiva de leyes de un sistema multiplicativo produce resultados que se acumulan en forma de producto. La capitalización de la unidad monetaria en el intervalo total es igual a la capitalización sucesiva en cada uno de los periodos. L(t ; s ) . L( s ; p) = L(t ; p) - Sistemas Unificables Un sistema es unificable si existe al menos una solución suma de capitales que no dependa de p, es decir válida para todas las leyes del sistema. Facultad de CC.EE. – Dpto. de Economía Financiera I Diapositiva 4 Matemática Financiera. Tema 3 – Sistemas financieros 1. Sistemas financieros. Tipología - Sistemas Unificables. n ∑ C L(t s =1 s s ; p ) = C L(τ ; p ) ∀p El capital (C;τ) se denomina capital unificado, su cuantía es sólo función de las cuantías de los capitales a unificar y el vencimiento τ se denomina vencimiento único o común. Todos los sistemas unificables admiten la solución media en la que el vencimiento es n t1<τ <tn siempre que C = ∑ Cs s =1 Facultad de CC.EE. – Dpto. de Economía Financiera I Diapositiva 5 Matemática Financiera. Tema 3 – Sistemas financieros 2. Capitalización simple Todo sistema de capitalización simple tiene la expresión L(t ; p ) = 1 + i ( p − t ) con p > t e i > 0 Se trata de un sistema estacionario, sumativo y unificable con solución única, la solución media. Expresado en forma estacionaria L( z ) = 1 + i ( z ) El valor del parámetro i, siempre asociado a la unidad de tiempo, es lo único que diferencia un sistema de capitalización simple de otro y su significado financiero es: Tanto acumulado constante para cualquier intervalo de tiempo µ (t1, t2) = i y tanto instantáneo acumulado para todo t µ (t, p) = i Facultad de CC.EE. – Dpto. de Economía Financiera I Diapositiva 6 Matemática Financiera. Tema 3 – Sistemas financieros 3. Capitalización compuesta Todo sistema de capitalización compuesta tiene la forma L(t ; p) = e k ( p −t ) =e kz con k > 0 , p > t , z = p − t > 0 o bien L(t ; p ) = (1 + i ) ( p −t ) = (1 + i ) z con i = e k − 1 > 0 Se trata de un sistema estacionario, multiplicativo y unificable con infinitas soluciones. Los parámetros k ó i que caracterizan un sistema de capitalización compuesta son dimensionados respecto del tiempo. Un cambio en la unidad de medida del tiempo en el sentido de que los vencimientos se multipliquen por m implica L(t ; p) = L(t.m ; p.m) (1 + i ) ( p −t ) = (1 + i ')m ( p −t )de donde i ' = (1 + i )1/ m − 1 Facultad de CC.EE. – Dpto. de Economía Financiera I Diapositiva 7 Matemática Financiera. Tema 3 – Sistemas financieros 3. Capitalización compuesta Los parámetros i e i’ son equivalentes y están referidos a distinta unidad de tiempo pero producen el mismo resultado al aplicarse sobre el mismo capital y por idéntico periodo de tiempo. Todas las magnitudes derivadas ordinarias del sistema de capitalización compuesta son constantes para intervalos de la misma amplitud. El significado financiero del parámetro k es el de tanto instantáneo ∂ log e L(t ; p ) ρ (t ; p ) = − = k = log e (1 + i ) ∂t El parámetro i es el rédito de capitalización para intervalos unitarios i (t , t + 1) = i Facultad de CC.EE. – Dpto. de Economía Financiera I Diapositiva 8 Matemática Financiera. Tema 3 – Sistemas financieros 3. Capitalización compuesta y también es el tanto efectivo de capitalización ρ (t , t + 1) = i El tanto efectivo es el tanto correspondiente a la unidad de tiempo, en el resto de los casos se llama tanto nominal. Cuando el periodo de capitalización es una fracción 1/m de año, el rédito y el tanto tienen notaciones específicas muy utilizadas en la práctica: 1 1 (m) Rédito; i (t , t + ) = i = (1 + i ) m − 1 m Tanto nominal de frecuencia m [ ] (m) 1 i 1 ρ (t , t + ) = = (1 + i ) m − 1 m = i / m ) m = j( m ) m 1/ m Facultad de CC.EE. – Dpto. de Economía Financiera I Diapositiva 9 Matemática Financiera. Tema 3 – Sistemas financieros 4. Descuento simple comercial Su expresión analítica es A(t ; p) = 1 − d (t − p ) con t ≥ p y d >0 Para identificar el sistema es necesario dar el valor numérico del parámetro d y la unidad de tiempo a la que va referido. Sus propiedades son análogas a las del sistema de capitalización simple y ambos se utilizan habitualmente en las operaciones financieras a corto plazo. Facultad de CC.EE. – Dpto. de Economía Financiera I Diapositiva 10 Matemática Financiera. Tema 3 – Sistemas financieros 5. Descuento compuesto Sus propiedades y características son análogas a las del sistema de Capitalización Compuesta. Suele expresarse en función de tres parámetros que tienen dimensión respecto al tiempo A(t ; p ) = e − k ( t − p ) = (1 − d ) (t − p ) = (1 + i ) − / t − p ) donde: ¾ k es el tanto instantáneo. ¾ d es el rédito de descuento para intervalos unitarios y el tanto efectivo de descuento. ¾ i es el rédito de contradescuento para intervalos unitarios y el tanto efectivo de la capitalización compuesta equivlente. Facultad de CC.EE. – Dpto. de Economía Financiera I Diapositiva 11 Matemática Financiera. Tema 3 – Sistemas financieros 6. Comparación entre Capitalización Simple y Compuesta. CAPITALIZACIÓN Para 1.000 unidades de capital y un rédito anual del 10%. SIMPLE 0 1 2 3 4 5 6 7 M E S E S 8 9 10 11 12 13 14 15 16 17 18 19 20 1.000,00 1.008,33 1.016,67 1.025,00 1.033,33 1.041,67 1.050,00 1.058,33 1.066,67 1.075,00 1.083,33 1.091,67 1.100,00 1.108,33 1.116,67 1.125,00 1.133,33 1.141,67 1.150,00 1.158,33 1.166,67 COMPUESTA 1.000,00 1.007,97 1.016,01 1.024,11 1.032,28 1.040,51 1.048,81 1.057,17 1.065,60 1.074,10 1.082,66 1.091,30 1.100,00 1.108,77 1.117,61 1.126,53 1.135,51 1.144,56 1.153,69 1.162,89 1.172,16 DIFERENCIA 0,00 0,36 0,65 0,89 1,05 1,16 1,19 1,16 1,06 0,90 0,67 0,37 0,00 -0,44 -0,95 -1,53 -2,17 -2,90 -3,69 -4,56 -5,50 Facultad de CC.EE. – Dpto. de Economía Financiera I Diapositiva 12 Matemática Financiera. Tema 3 – Sistemas financieros C a p ita l co n s titu id o 6. Comparación entre Capitalización Simple y Compuesta. 1190 1180 1170 1160 1150 1140 1130 1120 1110 1100 1090 1080 1070 1060 1050 1040 1030 1020 1010 1000 Capitalización Simple C(1+in) Capitalización compuesta C(1+i)^n 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 Duración (meses) Facultad de CC.EE. – Dpto. de Economía Financiera I Diapositiva 13 Matemática Financiera. Tema 3 – Sistemas financieros 6. Comparación entre Capitalización Simple y Compuesta. Diferencia entre capitalización compuesta y simple 6 5 4 3 2 1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 -1 -2 Duración (meses) Facultad de CC.EE. – Dpto. de Economía Financiera I Diapositiva 14 Matemática Financiera. Tema 3 – Sistemas financieros 7. Comparación entre Descuento Simple Comercial y Descuento Compuesto. DESCUENTO COMPUESTO DESCUENTO SIMPLE COMERCIAL Descuento compuesto