to get the file

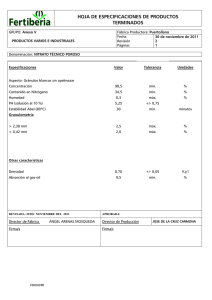
PROGRAMACIÓN
LINEAL
Introducción
♦ La programación lineal es instrumento
♦Características de un
programa lineal
♦Análisis geométrico de
programas lineales
♦Formulación de programas
lineales
♦Matrices y soluciones básicas
♦El método Simplex
Definición de programa lineal
habitual en empresas.
♦ Una de las ramas de la Optimización
más desarrollada.
Definición de programa lineal
♦ Función objetivo y restricciones lineales
⎧ opt F ( x ) = c x + c x + L + c x
⎪
⎪a x + a x + L + a x ≤ b
⎪⎪
⎨M
⎪
⎪a x + a x + L + a x ≤ b
⎪
⎪⎩ x , x , K x ≥ 0
1
11
1
m1
1
12
1
2
2
m 2
1
2
2
1n
2
n
1
n
mn
n
n
m
n
♦ Es convexo:
– Todo óptimo es global
– Las condiciones necesarias son suficientes
– Si hay dos soluciones distintas, también lo
es cualquier combinación lineal convexa
Análisis geométrico
⎧máx 3 x + 4 y
⎪
⎪⎪2 x + 3 y ≤ 10
⎨
⎪x + 3 y ≥ 5
⎪
⎪⎩ x, y ≥ 0
Máximo en el
(5,0): vértice
♦ Ventajas:
– Fáciles de definir y formular
– Se trabaja de forma eficiente con un
número elevado de variables de decisión
– Se adaptan mejor al tratamiento algorítmico
con computadores
Análisis geométrico
⎧máx 4 x + 6 y
⎪
⎪⎪2 x + 3 y ≤ 10
⎨
⎪x + 3 y ≥ 5
⎪
⎪⎩ x, y ≥ 0
Máximo en todos
los puntos de uno
de los lados del
polígono
1
Análisis geométrico
⎧máx 2 x + 3 y
⎪
⎪⎪ x + y ≥ 4
⎨
⎪x ≥ 2
⎪
⎪⎩ y ≥ 0
Análisis geométrico
♦ Deducción de propiedades:
– El espacio D de soluciones factibles es un
polítopo. Recomendable que sea acotado.
– Todo óptimo es global y siempre se alcanza
en la frontera de D (alguna restricción se
satura).
– Si existe óptimo, éste se alcanza, al menos,
en un vértice de D.
– Si varios puntos son óptimos, también
cualquier combinación lineal convexa.
D no acotado en
la dirección de
crecimiento de la
función
Formulación de programas
lineales
Análisis geométrico
♦ Primer método de resolución:
– Localizar los vértices de D.
– Calcular la función objetivo sobre todos los
vértices
– Elegir aquél sobre el que la función alcance
el menor o el mayor valor -> solución
– Si varios vértices son óptimos, también
cualquier combinación lineal convexa.
♦ Formulación estándar:
⎧ mín c x + c x + L + c x
⎪
⎪a x + a x + L + a x = b
⎪
⎪⎪ a x + a x + L + a x = b
⎨
⎪M
⎪
⎪a x + a x + L + a x = b
⎪
⎪⎩ x , x , K x ≥ 0 ; n ≥ m ; b ≥ 0 , i = 1 , 2 , K , m
♦ Formulación estándar matricial:
1
2
1
12
2
21
1
22
2
m1
1
No aconsejable para problemas
de grandes dimensiones
1
11
1
2
m 2
Formulación de p. lineales
2
i
i1
1
1
in
n
i
i1
1
n
in
n
– Si xi no está sujeta a la condición de no
negatividad: x = y − z con y , z ≥ 0
– Para que bi>=0, multiplicar por -1
i
i
i
i
2
n
n
m
i
♦ A matriz de m filas y n columnas, n>=m
in
i
a x + L + a x ≥ b ⇒ ∃ y ≥ 0 tal que a x + L + a x − y = b
i1
n
cx
⎧ mín
⎪⎪
Ax
=
b
⎨
⎪
⎪⎩ x ≥ 0
a x + L + a x ≤ b ⇒ ∃ y ≥ 0 tal que a x + L + a x + y = b
n
mn
1
Matrices y soluciones básicas
– máx f(x)= mín -f(x)
– mín c1x1+...cnxn+d=mín c1x1+...cnxn
– Variables de holgura:
in
n
n
2n
forma estándar:
1
n
1n
⎧ mín cx
⎪⎪
⎨ Ax = b
⎪
⎪⎩ x ≥ 0
♦ Transformación de un p. lineal a su
i1
2
i
i
♦ De rango m (no hay restricciones
redundantes)
Matriz básica: submatriz de A con det. no nulo
formada por m columnas de A
Si B es una de ellas, es básica factible si B-1b>=0
Variables naturales y variables de holgura
2
Matrices y soluciones básicas
Matrices y soluciones básicas
♦ Cada matriz básica B origina una
♦ Si xD=0 :
solución básica:
A = (B | D)
x
B
= B
Solución básica:
⎛x
x = ⎜⎜
⎝x
⎞ variables básicas
⎟
⎟ variables no básicas
⎠
⎛x ⎞
Ax = b ⇒ ( B D ) ⎜⎜ ⎟⎟ = Bx + Dx
⎝x ⎠
B
D
B
B
D
=b
D
⇓
x = B b − B Dx
−1
B
−1
D
−1
b
⎛x ⎞
x = ⎜⎜ ⎟⎟
⎝0⎠
B
♦ Construcción de soluciones básicas :
– Bxb=b y dando valores nulos a las restantes
variables
♦ Soluciones básicas :
– Factibles si xb>=0
• Degeneradas: alguna v. Básica es nula
• No degeneradas: xb>0
– Infactibles si alguna v. básica es negativa
Matrices y soluciones básicas
Matrices y soluciones básicas
♦ Interpretación geométrica de las
♦ Las soluciones básicas factibles de:
soluciones básicas:
⎧mín 3 x + 4 y Soluciones básicas factibles:
⎪
(5,0,0,0)
⎪⎪2 x + 3 y ≤ 10
(0,5/3,5,0)
⎨
(0,10/3,0,5)
⎪x + 3 y ≥ 5
⎪
⎪⎩ x, y ≥ 0
cx
⎧ mín
⎪⎪
Ax
=
b
⎨
⎪
⎩⎪ x ≥ 0
se corresponden con los vértices de D.
♦ Teorema fundamental de la
programación lineal: dado un programa
lineal en forma estándar, si existe
solución óptima, ésta se alcanza al
menos sobre una de las soluciones
básicas factibles.
El método Simplex
El método Simplex
♦ Encontrar la solución básica óptima sin
♦ En un número finito de pasos se
tener que construirlas todas, sólo
utilizando un subconjunto:
– Se parte de una solución básica factible
inicial.
– Si no es óptima, encontrar otra que
disminuya el valor de la función objetivo o
que, por lo menos, no aumente.
– Repetir el proceso hasta encontrar una
solución básica factible óptima.
encuentra el óptimo. Para ello se
necesita:
– Un test de optimalidad que permita
reconocer cuándo una solución básica
factible es óptima.
– Un método efectivo de paso de una
solución básica a otra que mejore el valor
de la función objetivo.
3
El método Simplex
El método Simplex
♦ Test de optimalidad:
vértice óptimo
vértice inicial
D
El método Simplex
cx
⎧ mín
⎪⎪
⎨ Ax = b
⎪
⎪⎩ x ≥ 0
(C2)
xB1
....
xBm
(C3)
c1
b1
a11
....
bm
am1
cB ο b cB ο A1
z1
– Teorema: una solución básica factible es
óptima si y sólo si
r=cD-cBB-1 D>=0
Se demonina a r el vector de costes
reducidos
–Teorema: si existe una solución básica factible
en la que r>0, esa solución básica es el único
óptimo del problema.
El método Simplex
♦ Método del Simplex en forma de tabla:
(C1)
cB1
....
cBm
cx
⎧ mín
⎪⎪
Ax
=
b
⎨
⎪
⎪⎩ x ≥ 0
....
....
....
....
....
....
....
....
....
....
cn
a1n
(F1)
amn
cB ο An (Fm+2)
zn
(F1)- (Fm+2)
Cada tabla está asociada a una solución básica factible
♦ Si todos los elementos de la última fila
son mayores o iguales a 0, se ha
alcanzado el óptimo.
♦ Si los valores de la última fila asociados
a las variables no básicas,( r ), son >0, la
solución es el único óptimo.
Importante:
• Los elementos de C3 salvo el último, deben ser >=0
•Las columnas de A asociadas a las variables básicas forman
la matriz identidad
4