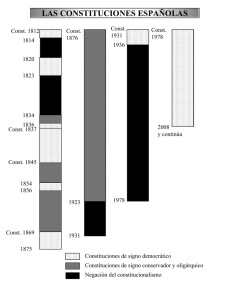
Primer parcial de EDA Facultad de Informática de Valencia 10 de
Anuncio

Primer parcial de EDA
Facultad de Informática de Valencia
10 de junio de 2009 – Duración 2 horas
No olvides poner el nombre. No utilices lápiz ni tinta roja. Se piden siempre soluciones eficientes.
Pregunta 1 (3 puntos) Un montı́culo o heap representa, en forma de vector, un árbol binario casicompleto:
c l a s s MaxHeap {
i n t ∗v ;
// v e c t o r i n d e x a d o
i n t tamanyo ; // d e l v e c t o r
i n t ocupados ; // v a l o r e n t r e 0 y
public :
...
i n t sumaElementosProfundidad ( i n t
i n t sumaElementosRamaIzquierda ( )
};
d e s d e 1 h a s t a tamanyo
tamanyo
p r o f ) const ; // EXAMEN
const ;
// EXAMEN
Se pide implementar los siguientes métodos en la clase MaxHeap:
a) El método sumaElementosProfundidad que devuelve la suma de aquellos nodos del árbol que se
encuentren a la profundidad dada como argumento (1.5 puntos)
b) El método sumaElementosRamaIzquierda que devuelve la suma de los nodos del camino que parte
de la raı́z bajando por el hijo izquierdo mientras se pueda seguir bajando (1.5 puntos)
Solución:
i n t min ( i n t a , i n t b ) { return ( a<b ) ? a : b ; }
i n t MaxHeap : : sumaElementosProfundidad ( i n t p r o f ) const {
i n t f i r s t i n d e x = 1<<p r o f ;
i n t l a s t i n d e x = min ( ocupados , 2∗ f i r s t i n d e x −1) ;
int r e s u l t a d o = 0 ;
f o r ( i n t i=f i r s t i n d e x ; i <l a s t i n d e x ; ++i )
r e s u l t a d o += v [ i ] ;
return r e s u l t a d o ;
}
i n t MaxHeap : : sumaElementosRamaIzquierda ( ) const {
int r e s u l t a d o = 0 ;
f o r ( i n t i =1; i<=ocupados ; i ∗= 2 )
r e s u l t a d o += v [ i ] ;
return r e s u l t a d o ;
}
Pregunta 2 (3 puntos) Dada la siguiente implementación de una tabla de dispersión
struct node {
char ∗ v a l u e ;
node ∗ next ;
};
c l a s s HashTable {
i n t t a b l e S i z e ; // t a l l a d e l v e c t o r t a b l e
node ∗∗ t a b l e ; // v e c t o r de p u n t e r o s a node
i n t hash ( char ∗ c l v ) ; // d e v u e l v e un e n t e r o e n t r e 0 y t a b l e S i z e −1
public :
HashTable ( i n t numCubetas ) ;
˜ HashTable ( ) ;
void i n s e r t ( char ∗ cadena ) ; // EXAMEN
bool operator== ( const HashTable &o t h e r ) const ; // EXAMEN
};
a) Implementa el método insert que mantenga el orden lexicográfico de menor a mayor las listas de
elementos de cada cubeta (1.5 puntos).
b) Implementa la comparación de dos tablas. Dos tablas se consideran iguales si tienen el mismo
número de cubetas y todas las listas contienen exactamente los mismos elementos (y en el mismo
orden, puesto que están ordenadas) (1.5 puntos).
Solución:
void HashTable : : i n s e r t ( char ∗ cadena ) {
node ∗∗p = &( t a b l e [ hash ( cadena ) ] ) ;
while ( ( ∗ p ) != 0 && strcmp ( ( ∗ p )−>v a l u e , cadena ) <0)
p = &((∗p )−>next ) ;
i f ( ( ∗ p ) == 0 | | strcmp ( ( ∗ p )−>v a l u e , cadena ) !=0) {
∗p = new node (new char [ s t r l e n ( cadena ) +1] ,∗ p ) ;
s t r c p y ( ( ∗ p )−>v a l u e , cadena ) ;
}
}
bool HashTable : : operator== ( const HashTable &o t h e r ) const {
i f ( t a b l e S i z e != o t h e r . t a b l e S i z e ) return f a l s e ;
f o r ( i n t i =0; i <t a b l e S i z e ; ++i ) {
f o r ( node ∗ a=t a b l e [ i ] , ∗b=o t h e r . t a b l e [ i ] ; a !=0 && b ! = 0 ; a=a−>next , b
=b−>next )
i f ( strcmp ( a−>v a l u e , b−>v a l u e ) !=0)
return f a l s e ;
i f ( a !=0 | | b !=0) return f a l s e ;
}
return true ;
}
Pregunta 3 (2 puntos) Implementa el método contarHojas que cuenta el número elementos en el
mfset que son hojas del bosque.
class mfset {
i n t n , ∗ vec ; // v e c e s de t a l l a n
public :
m f s e t ( i n t numElem ) {
n = numElem ; vec = new i n t [ n ] ;
f o r ( i n t i =0; i <n;++ i ) vec [ i ] = −1;
}
˜ m f s e t ( ) ; // d e s t r u c t o r
void merge ( i n t u , i n t v ) ;
int f i n d ( int u) ;
i n t c o n t a r H o j a s ( ) const ; // EJERCICIO DE EXAMEN
};
Solución:
i n t m f s e t : : c o n t a r H o j a s ( ) const {
bool ∗ e s h o j a = new bool [ n ] ;
f o r ( i n t i =0; i <n;++ i ) e s h o j a [ i ]
= true ;
f o r ( i n t i =0; i <n;++ i )
i f ( vec [ i ] >= 0 )
e s h o j a [ vec [ i ] ] = f a l s e ;
i n t numhojas = 0 ;
f o r ( i n t i =0; i <n;++ i )
i f ( e s h o j a [ i ] ) numhojas++;
delete [ ] e s h o j a ;
return numhojas ;
}
Pregunta 4 (2 puntos) Queremos juntar dos ficheros ya ordenados para obtener otro fichero también
ordenado. Cada fichero contiene un número entero por lı́nea. Escribe un programa que, con coste lineal
genera dicho fichero, el programa recibe como argumentos el nombre de los dos ficheros origen y el nombre
del fichero destino, como muestra el siguiente ejemplo:
> cat a.txt
10
30
100
>cat b.txt
5
25
> examen a.txt b.txt c.txt ; cat c.txt
5
10
25
30
100
Solución:
#include <f s t r e a m >
using namespace s t d ;
i n t main ( i n t argc , char ∗∗ argv ) {
i f s t r e a m f 1 ( argv [ 1 ] ) , f 2 ( argv [ 2 ] ) ; o f s t r e a m f 3 ( argv [ 3 ] ) ;
int a , b ;
bool hay a = ( f 1 >> a ) , hay b = ( f 2 >> b ) ;
while ( hay a && hay b )
i f ( a < b ) { f 3 << a << e n d l ; hay a = ( f 1 >> a ) ; }
else
{ f 3 << b << e n d l ; hay b = ( f 2 >> b ) ; }
while ( hay a ) { f 3 << a << e n d l ; hay a = ( f 1 >> a ) ; }
while ( hay b ) { f 3 << b << e n d l ; hay b = ( f 1 >> b ) ; }
f1 . close () ; f2 . close () ; f3 . close () ;
return 0 ;
}