Guía para la resolución de problemas
Anuncio
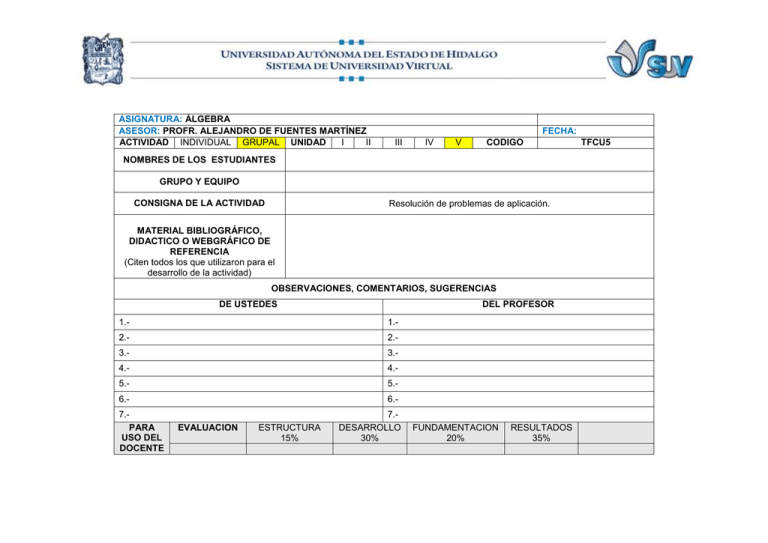
ASIGNATURA: ÁLGEBRA ASESOR: PROFR. ALEJANDRO DE FUENTES MARTÍNEZ ACTIVIDAD INDIVIDUAL GRUPAL UNIDAD I II FECHA: III IV V CODIGO NOMBRES DE LOS ESTUDIANTES GRUPO Y EQUIPO CONSIGNA DE LA ACTIVIDAD Resolución de problemas de aplicación. MATERIAL BIBLIOGRÁFICO, DIDACTICO O WEBGRÁFICO DE REFERENCIA (Citen todos los que utilizaron para el desarrollo de la actividad) OBSERVACIONES, COMENTARIOS, SUGERENCIAS DE USTEDES DEL PROFESOR 1.- 1.- 2.- 2.- 3.- 3.- 4.- 4.- 5.- 5.- 6.- 6.- 7.PARA USO DEL DOCENTE EVALUACION ESTRUCTURA 15% 7.DESARROLLO 30% FUNDAMENTACION 20% RESULTADOS 35% TFCU5 Introducción Una de las razones principales para estudiar álgebra, y matemáticas en general, es que las podemos utilizar para resolver problemas de la vida diaria. Para resolver de forma matemática la mayor parte de los problemas de aplicación de la vida real, necesitamos ser capaces de expresar el problema en símbolos matemáticos usando expresiones o ecuaciones, y cuando lo hacemos, creamos un modelo matemático de la situación. Se les presenta a continuación un resumen de la guía para la resolución de problemas, basada en la propuesta del matemático George Polya. Guía para la resolución de problemas 1. Entender el problema. 2. Traducir el problema a lenguaje matemático. 3. Realizar los cálculos matemáticos necesarios para resolver el problema. 4. Comprobar la respuesta obtenida en el paso 3. 5. Responder la pregunta. Actividad Colaborativa Instrucciones: Resuelvan trabajando colaborativamente y aplicando el método de resolución de problemas de George Polya el siguiente conjunto de problemas de aplicación. 2 Problema 1. Costo de lavandería. A Emilio Pérez le cuesta $65 pesos a la semana lavar y secar su ropa en la lavandería de la esquina. Si una lavadora con secadora cuesta un total de $1,560 ¿Cuántas semanas tomaría para que el costo de la lavandería fuese igual al costo de la lavadora con secadora? ¿Y cuántos meses? (No tomen en cuenta el costo de la energía eléctrica) Problema 2. Costo de una cena. Los cinco miembros de la familia Hernández van a cenar con tres miembros de la familia López. Antes de la cena, deciden que los Hernández pagarán 5 8 de la 3 cuenta (sin la propina) y los López pagarán 8 más toda la propina del 15%. Si la cuenta total, incluido el 15% de propina, es de $884.60. ¿Cuánto pagará cada familia? Problema 3. Plantas y animales. En el mundo existen aproximadamente 1,500,000 especies clasificadas como plantas, animales o insectos. Los insectos a su vez están subdivididos en escarabajos e insectos que no son escarabajos. Existen aproximadamente 100,000 más plantas que animales. Existen 290,000 más insectos no escarabajos que animales. El número de escarabajos es 140,000 menos que dos veces el número de animales. Encuentren el número de animales, plantas, insectos no escarabajos y escarabajos. Problema 4. ¿Cómo se eliminan las fracciones en una ecuación?. 1 1 Cuando le pidieron a Rocío que resolviera la ecuación 2 𝑥 + 3 = 1 𝑥 4 1 − 2, aseguró que para eliminar las fracciones, el lado izquierdo debería multiplicarse por 6 y el derecho debería multiplicarse por 8. Esto es incorrecto. ¿Por qué esto es incorrecto? Expliquen su respuesta. ¿Cuál es el número único por el que debe multiplicarse toda la ecuación para eliminar las fracciones? Resuelvan la ecuación de forma correcta. 3 Problema 5. Barcos en el mar. El portaviones USS John F Kennedy y el submarino nuclear USS Memphis partieron al mismo tiempo de la estación naval Puget Sound dirigiéndose al mismo destino en el Océano Índico. El portaviones viaja a su velocidad máxima de 34.5 kilómetros por hora y el submarino viaja sumergido a su velocidad máxima de 20.2 kilómetros por hora. El portaviones y el submarino viajan a esas velocidades hasta que están a 100 kilómetros de separación. ¿Cuánto tiempo pasará para que el portaviones y el submarino estén a 100 kilómetros de separación? Problema 6. Ventas en un puesto de hot dogs. El puesto de hot dogs de Mario en Chicago vende hot dogs por $2.00 cada uno y tacos de bistec por $2.25 cada uno. Si la venta total del día fue de $585.50 y se vendieron 278 productos, ¿Cuántos de cada uno se vendieron? Problema 7. Alcance de radio comunicadores. Un equipo de radio comunicadores RS446 tiene un alcance de alrededor de dos kilómetros. Alicia y María inician una caminata a lo largo de un sendero natural en direcciones opuestas, llevando sus radio comunicadores. Si Alicia camina a una velocidad de 3.8 kmph y María camina a una velocidad de 4.2 kmph, ¿Cuánto tiempo tardarán en estar fuera del alcance de los radio localizadores? Problema 8. Dos trabajos. Alonso Torres trabaja en dos empleos de tiempo parcial. Uno paga $57.50 por hora y el otro $68.25 por hora. La semana anterior Alonso ganó un total de $1190.50 y trabajó un total de 24 horas. ¿Cuántas horas trabajó en cada empleo? Problema 9. Sistema de ecuaciones lineales. Resolviendo para x y y, determinen la solución para el siguiente sistema de ecuaciones: 4𝑎𝑥 + 3𝑦 = 19 −𝑎𝑥 + 𝑦 = 4 4 Problema 10. Cambio en la fuerza laboral. El porcentaje de hombres en la fuerza laboral está disminuyendo de manera constante mientras que el porcentaje de mujeres está aumentando. La función ℎ(𝑡) = −0.25𝑡 + 85.4, donde 𝑡 = 𝑎ñ𝑜𝑠 desde 1955, puede usarse para estimar el porcentaje de hombres en la fuerza laboral, y la función 𝑚(𝑡) = −0.52𝑡 + 35.7 puede usarse para estimar el porcentaje de mujeres en la fuerza laboral. Si esta tendencia continúa, determinen el año (de este siglo) en que el porcentaje de mujeres en la fuerza laboral será igual al porcentaje de hombres. (La clave aquí es igualar las dos ecuaciones del sistema). Problema 11. Cámaras digitales. Alan acaba de comprar una nueva cámara digital, una tarjeta de memoria de 128 megabytes (MB) y una tarjeta de memoria de 512 MB. La tarjeta de 512 MB puede almacenar cuatro veces más fotos que la tarjeta de 128 MB. Juntas las dos tarjetas de memoria pueden almacenar 360 fotos (de óptima calidad). Determina cuántas fotos puede almacenar cada una de las cámaras. Problema 12. Impresoras de fotografías. En la revista del Consumidor de julio de 2005, apareció un reportaje sobre impresoras de fotografías que comparaban el costo de imprimirlas en cada una de las impresoras. La más cara de las impresoras de fotos de 4 X 6 fue la Olympus P-5100. La menos cara fue la Epson Picture Mate. La impresión de una foto en ambas impresoras costaría $0.80. El costo de imprimir una foto en la Olympus es $0.20 más que el doble del costo de imprimir una foto en la Epson. Determinen el costo de imprimir una foto en cada impresora. 5 Problema 13. Utilidad. La utilidad de la compañía Frigs, que vende refrigeradores, es 𝑈(𝑛) = 6.2𝑛2 + 6𝑛 − 3, donde 𝑈(𝑛) son dólares. a) Determinen la utilidad cuando se venden 7 refrigeradores. b) ¿Cuántos refrigeradores deben venderse para obtener una ganancia de $675? Problema 14. Lanzamiento de una pelota. Luisa se encuentra parada en la parte superior de un edificio, y lanza una pelota hacia arriba desde una altura de 30 metros, con una velocidad de 2 1 metros por segundo. Utilicen la fórmula ℎ = 2 𝑔𝑡 2 + 𝑣𝑜 𝑡 + ℎ0 para responder las preguntas siguientes. a) A partir de su lanzamiento, ¿Cuánto tiempo tardará la pelota en estar a 7 metros respecto del piso? b) A partir de su lanzamiento, ¿Cuánto tiempo tardará la pelota en golpear el suelo? Problema 15. Expectativa de vida. La función 𝑁(𝑡) = 0.0054𝑡 2 − 1.46𝑡 + 95.11 puede usarse para calcular el promedio de número de años de expectativa de vida para una persona de t años de edad, donde 30 ≤ t ≤100. a) Calculen la expectativa de vida para una persona de 40 años de edad. b) Si una persona tiene una expectativa de vida de 14.3 años, calculen su edad actual. (apliquen la fórmula general para resolver este inciso) 6











