Ecuaciones de segundo grado

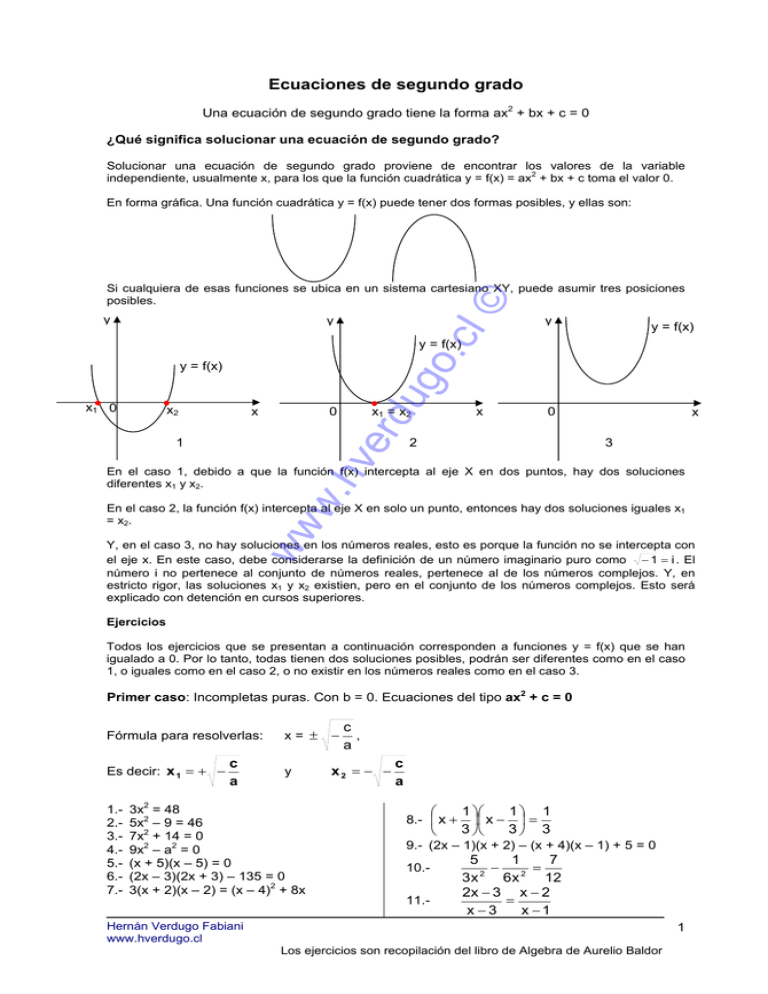
Ecuaciones de segundo grado
Una ecuación de segundo grado tiene la forma ax2 + bx + c = 0
¿Qué significa solucionar una ecuación de segundo grado?
Solucionar una ecuación de segundo grado proviene de encontrar los valores de la variable
independiente, usualmente x, para los que la función cuadrática y = f(x) = ax2 + bx + c toma el valor 0.
En forma gráfica. Una función cuadrática y = f(x) puede tener dos formas posibles, y ellas son:
y
©
Si cualquiera de esas funciones se ubica en un sistema cartesiano XY, puede asumir tres posiciones
posibles.
y
y = f(x)
.c
l
y
o
y = f(x)
•
x1 0
•x
0
x
2
•x
1
= x2
x
0
2
x
3
v
1
e
rd
u
g
y = f(x)
w
w
.h
En el caso 1, debido a que la función f(x) intercepta al eje X en dos puntos, hay dos soluciones
diferentes x1 y x2.
En el caso 2, la función f(x) intercepta al eje X en solo un punto, entonces hay dos soluciones iguales x1
= x2.
w
Y, en el caso 3, no hay soluciones en los números reales, esto es porque la función no se intercepta con
el eje x. En este caso, debe considerarse la definición de un número imaginario puro como − 1 = i . El
número i no pertenece al conjunto de números reales, pertenece al de los números complejos. Y, en
estricto rigor, las soluciones x1 y x2 existien, pero en el conjunto de los números complejos. Esto será
explicado con detención en cursos superiores.
Ejercicios
Todos los ejercicios que se presentan a continuación corresponden a funciones y = f(x) que se han
igualado a 0. Por lo tanto, todas tienen dos soluciones posibles, podrán ser diferentes como en el caso
1, o iguales como en el caso 2, o no existir en los números reales como en el caso 3.
Primer caso: Incompletas puras. Con b = 0. Ecuaciones del tipo ax2 + c = 0
Fórmula para resolverlas:
Es decir: x 1 = + −
1.2.3.4.5.6.7.-
c
a
x= ± −
y
3x2 = 48
5x2 – 9 = 46
7x2 + 14 = 0
9x2 – a2 = 0
(x + 5)(x – 5) = 0
(2x – 3)(2x + 3) – 135 = 0
3(x + 2)(x – 2) = (x – 4)2 + 8x
c
,
a
x2 = − −
c
a
⎛
⎝
8.- ⎜ x +
1 ⎞⎛
1⎞ 1
⎟⎜ x − ⎟ =
3 ⎠⎝
3⎠ 3
9.- (2x – 1)(x + 2) – (x + 4)(x – 1) + 5 = 0
10.11.-
5
1
7
− 2 =
2
12
3x
6x
2x − 3 x − 2
=
x−3
x −1
Hernán Verdugo Fabiani
www.hverdugo.cl
1
Los ejercicios son recopilación del libro de Algebra de Aurelio Baldor
12.13.-
x 2 − 5 4 x 2 − 1 14 x 2 − 1
+
−
=0
3
5
15
x2 + 1
2x − 3 −
= −7
x−2
3−
14.-
3
4x 2 − 1
=2
Segundo caso. Incompletas binomiales. Con c = 0. Son del tipo ax2 + bx = 0
1.2.3.4.5.-
x2 = −
y
b
a
x2 = 5x
4x2 = -32x
x2 – 3x = 3x2 – 4x
5x2 + 4 = 2(x + 2)
(x – 3)2 – (2x + 5)2 = -16
6.-
x2 x − 9 3
−
=
3
6
2
7.-
(4x -1)(2x + 3) = (3x + 3)(x – 1)
x +1 x + 4
=
=1
x −1 x − 2
8.-
Ecuaciones completas
.h
v
x2 – 3x + 2 = 0
x2‘ – 2x – 15 = 0
x2 = 19x – 88
x2 + 34x = 285
5x(x – 1) – 2(2x2 – 7x) = - 8
o
x2 =
y
− b − b 2 − 4c
2
6.7.8.9.10.-
x2 – (7x + 6) = x + 59
(x – 1)2 + 11x + 199 = 3x2 – (x – 2)2
(x – 2)(x + 2) – 7(x – 1) = 21
2x2 – (x – 2)(x + 5) = 7(x + 3)
(x – 1)(x + 2) – (2x – 3)(x + 4) – x + 14 = 0
w
w
1.2.3.4.5.-
− b + b 2 − 4c
2
g
Es decir: x 1 =
− b ± b 2 − 4c
2
e
rd
u
Fórmula de solución: x =
.c
l
Caso particular. Con a = 1. Son del tipo x2 + bx + c = 0
©
Soluciones: x1 = 0
w
Caso general. Son del tipo ax2 + bx + c = 0
− b ± b 2 − 4ac
Fórmula de solución: x =
2a
− b + b 2 − 4ac
Es decir: x 1 =
2a
y
1.2.3.4.5.6.7.8.9.-
3x2 – 5x + 2 = 0
4x2 + 3x – 22 = 0
x2 + 11x = -24
x2 = 16x – 63
12x – 4 – 9x2 = 0
5x2 – 7x – 90 = 0
6x2 = x + 222
x + 11 = 10x2
49x2 – 70x + 25 = 0
19.20.21.22.23.24.-
x(x + 3) = 5x + 3
3(3x – 2) = (x + 4)(4 – x)
9x + 1 = 3(x2 – 5) – (x – 3)(x + 2)
(2x – 3)2 – (x + 5)2 = - 23
25(x + 2)2 = (x – 7)2 – 81
3x(x – 2) – (x – 6) = 23(x – 3)
− b − b 2 − 4ac
x2 =
2a
10.11.12.13.14.15.16.17.18.-
12x – 7x2 + 64 = 0
x2 = - 15x – 56
32x2 + 18x – 17 = 0
176x = 121 + 64x2
8x + 5 = 36x2
27x2 + 12x – 7 = 0
15x = 25x2 + 2
8x2 – 2x – 3 = 0
105 = x + 2x2
25.7(x – 3) – 5(x2 – 1) = x2 – 5(x + 2)
26.- (x – 5)2 – (x – 6)2 = (2x – 3)2 – 118
27.- (5x – 2)2 – (3x + 1)2 – x2 – 60 = 0
28.- (x + 4)2 – (x – 3)2 = 343
29.- (x + 2)2 – (x – 1)2 = x(3x + 4) + 8
30.- (5x - 4)2 – (3x + 5)(2x – 1) = 20x(x – 2) + 27
Hernán Verdugo Fabiani
www.hverdugo.cl
2
Los ejercicios son recopilación del libro de Algebra de Aurelio Baldor
37.38.39.40.-
46.47.48.-
©
36.-
45.-
l
35.-
44.-
x
x−2 5
=
−
x−2
x
2
2
4x
1 − 3 x 20 x
−
=
x −1
4
3
3x − 1
2x
7
− =0
−
x
2x − 1 6
5x − 8 7x − 4
=
x −1
x+2
x + 3 5x − 1
−
=0
2x − 1 4 x + 7
1
1
1
− =
4 − x 6 x +1
x+4 x+2
1
=
−
x + 5 x + 3 24
5
6
5
−
=3
2
x +1
8
x
x − 1 x + 1 2x + 9
=
+
x +1 x −1 x + 3
3
1
1
−
=
x + 2 x − 2 x +1
.c
34.-
43.-
49.-
o
33.-
42.-
g
32.-
41.-
50.-
e
rd
u
31.-
x2 x 3
− =
5 2 10
13 3
4x −
=
x 2
x2 x
− = 3( x − 5)
6 2
1
2
1
( x − 4) + ( x − 5) = ( x 2 − 53 )
4
5
5
5
1
−
=1
x x+2
15 11x + 5
−
= −1
x
x2
8x
5x − 1
+
=3
3x + 5 x + 1
1
1
1
−
=
x − 2 x −1 6
2x − 3 x − 2
1−
=
x+5
10
x − 13
10(5 x + 3)
=5−
x
x2
12.13.-
.h
w
w
x2 – x – 6 = 0
x2 + 7x = 18
8x – 65 = - x2
x2 = 108 – 3x
2x2 + 7x – 4 = 0
6x2 = 10 – 11x
20x2 – 27x = 14
7x = 15 – 390x2
60 = 8x2 + 157x
x(x – 1) – 5(x – 2) = 2
(x – 2)2 – (2x + 3)2 = -80
w
1.2.3.4.5.6.7.8.9.10.11.-
v
Resolver mediante procedimiento de factorización.
6 9
4
− =−
2
x
3
x
x+2
74
+x=
x
x
14.15.16.17.18.-
19.20.-
(x + 2)2 − 2x − 5 = 3
3
x
3 x + 15
+x=
x−2
4
6
4 5
− =
x − 4 x 12
(x – 2)3 – (x – 3)3 = 37
x −1
x+3
−2=
x +1
3
4 x − 1 2x + 1
=
2x + 3 6 x + 5
3x + 2
9 x + 14
=5−
4
12 x
Ecuaciones literales.
1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.-
x2 + 2ax – 35a2 = 0
10x2 = = 36a2 – 3ax
a2x2 + abx – 2b2 = 0
89bx = 42x2 + 22b2
x2 + ax = 20a2
2x2 = abx + 3a2b2
b2x2 + 2abx = 3a2
x2 + ax – bx = ab
x2 – 2ax = 6ab – 3bx
3(2x2 – mx) + 4nx – 2mn = 0
x2 – a2 – bx – ab = 0
abx2 – x(b – 2a) = 2
x2 – 2ax + a2 – b2 = 0
4x(x – b) + b2 = 4m2
x2 – b2 + 4a2 – 4ax = 0
16.17.18.19.20.21.22.23.24.-
x2 – (a + 2)x = - 2a
x2 + 2x(4 – 3a) = 48a
x2 – 2x = m2 + 2m
x2 + m2x(m – 2) = 2m5
6x2 – 15ax = 2bx – 5ab
3x a x 2
+ −
=0
4 2 2a
2x − b 2bx − b 2
=
2
3x
a + x a − 2x
+
= −4
a−x a+x
x2
a2
=
x − 1 2(a − 2)
Hernán Verdugo Fabiani
www.hverdugo.cl
3
Los ejercicios son recopilación del libro de Algebra de Aurelio Baldor
25.-
x+
2 1
= + 2a
x a
26.-
2x − b
x
2x
−
=
b
x + b 4b
Ecuaciones irracionales de segundo grado. Es indispensable comprobar las dos raíces
que se encuentran.
3.4.5.6.7.8.-
x+3 +
11.-
x+
12.-
6
=5
x+3
4
=5
x
2 x = x+7 +
8
x+7
13.-
x+ x+8 = 2 x
14.-
6 − x + x + 7 − 12x + 1 = 0
2x + 4 x − 3 = 3
w
w
w
.h
v
e
rd
u
g
o
.c
9.-
10.-
©
2.-
x + 4x + 1 = 5
2x − x − 1 = 3 x − 7
5x − 1 + x + 3 = 4
2 x − x+5 =1
2x − 1 + x + 3 = 3
x − 3 + 2x + 1 − 2 x = 0
5 x − 1 − 3 − x = 2x
3 x + 1 5 x = 16 x + 1
l
1.-
Hernán Verdugo Fabiani
www.hverdugo.cl
4
Los ejercicios son recopilación del libro de Algebra de Aurelio Baldor