Modelos de problemas de Climatología Agrícola

Modelos de problemas de Climatología Agrícola 1. Las temperaturas máxima absoluta (Ta), media de máximas (Tm), media de mínimas (tm) y mínima absoluta (ta) de un determinado mes en los últimos 10 años han sido: Ta Tm tm ta 1988 19.3 16.1 2.8 ­6.4 1989 18.0 14.6 6.7 ­1.8 1990 18.0 15.0 4.8 0.0 1991 20.0 16.0 9.3 2.6 1992 20.6 15.4 6.2 0.0 1993 22.0 16.5 3.4 ­5.0 1994 19.0 16.2 8.1 2.5 1995 22.0 17.1 5.1 2.0 1996 18.0 15.0 5.7 ­0.5 1997 19.0 14.0 5.6 ­2.0 Calculad para la serie de 10 años, la temperatura máxima absoluta, la temperatura media de máximas absolutas, la temperatura media de máximas, la temperatura media, la temperatura media de mínima, la temperatura media de mínimas absoluta y la temperatura mínima absoluta en el mes considerado. Resultado: temper atur a máxima absoluta: 22 ºC temper atur a media de máximas absolutas: 19.59 ºC temper atur a media de máximas: 15.59 ºC temper atur a media: 10.68 ºC temper atur a media de mínima: 5.77 ºC la temper atur a media de mínimas absoluta: ­ 0.86 ºC temper atur a mínima absoluta en el mes consider ado: ­ 6.4 ºC 2. En un determinado día un pluviómetro recoge 1260 cm 3 . a) ¿Cuánto ha sido la lluvia expresada en m 3 /ha, si suponemos que el pluviómetro tiene una superficie captadora circular de 20 cm de diámetro? b) ¿Cuál ha sido la variación del nivel de agua en cm de un tanque evaporímetro de 1,2 metros de diámetro ese día, si la evaporación fue de 3 mm? c) En las mismas condiciones anteriores de lluvia y evaporación, ¿cuál ha sido la variación del volumen de agua en litros del tanque evaporímetro? d) Si la lluvia cayó en un periodo de 4 horas, ¿cuál fue la intensidad media de la misma en mm/h?. Resultado: Super ficie del pluviómetr o: S = 10 2 p = 314.16 cm 2 Altur a de lluvia: H = 1260 / 314.16 = 4.01 cm a) 10000 m 2 /ha ∙ 4.01 cm = 401 m 3 /ha b) 40.1 ­ 3 = 37.1 mm ha subido el nivel c) V = 3.71 cm ∙ 60 2 p cm 2 = 41.96 litr os d) I = 40,1 / 4 = 10,025 mm/h 3. Encontrad la relación entre la velocidad media del viento en 24 horas (V24) y la velocidad del viento diurno (Vd) (considerando diurno de las 7 a las 19 horas) si sabemos que la relación entre viento diurno y viento nocturno (Vd/Vn) es igual a 2,5. Resultado: Recor rido 24 h = V24 ∙ 24 = Vd∙12 + Vn∙ 12; V24 = (Vn + Vd) / 2 = ( (Vd/2,5) + Vd) / 2 = 0,7 Vd; Vd/V24 = 1,43
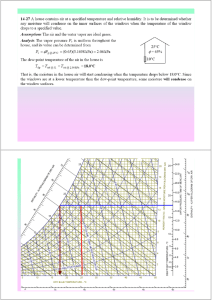
4. El balance de energía de la superficie del suelo se puede considerar que viene dado por la ecuación Rn= H+G+L∙ET donde Rn es la radiación neta, H es el flujo de calor sensible a la atmósfera, G es la energía utilizada en calentar el suelo, y L∙ET es el flujo de calor latente. Si durante un periodo de tiempo dado, los valores medios diarios de los componentes del balance de energía son: Rn = 428 cal /(cm 2 día); H = 72 cal/(cm 2 día); G= 4 cal/(cm 2 día); y tomando como calor latente de vaporización L=585 cal/g, calculad el valor medio de la evapotranspiración en mm/día. Resultado: L∙ET = Rn ­ G ­ H = 428 ­ 72 ­ 4 = 352 cal /(cm 2 día); ET = 352 / 585 = 0.602 g / (cm 2 día); Si consideramos una densidad del agua de 1 g/cm 3 ET == 0.602 (g / (cm 2 día) ) / 1 (g/cm 3 ) = 6.02 mm/día 5. Calculad la radiación recibida por una superficie de agua en W/m 2 , si la evaporación fue de 5 mm/día y la temperatura del aire fue de 25ºC. Considerad que el calor latente de vaporización viene dado por la expresión L (kJ/kg) = 2501­2,36∙t (donde t es la temperatura en ºC), y la densidad del agua a 25ºC es 995 kg/m 3 . Asumid que toda la energía recibida se utiliza para evaporar el agua. Resultado: L = 2501 – 2,36 ∙ 25 = 2442 kJ /kg E = 5 mm/día = 5 litr os/(m 2 día) = 5 ∙ 0,995 kg/(m 2 día) = 4,975 kg/(m 2 día) Rn = L ∙ E = 4,975 ∙ 2442 = 12148,95 kJ/(m 2 día) = 12148950 (J/(m 2 día) ) / 86400 (s/día) = 140,61 W/m 2 6. La temperatura del termómetro seco de un psicrómetro es de 24ºC y la del termómetro húmedo 20ºC. Indicad con ayuda del diagrama: a) La humedad relativa del aire y el déficit de saturación.; b) El valor mínimo que podría alcanzar la temperatura del aire sin que apareciera condensación; c) La humedad relativa del aire si la temperatura bajara hasta 19ºC. Resultado: Humedad r elativa: 70% Déficit de satur ación: 7 g/m 3 T. punto de r ocío: 18 ºC Humedad r elativa a 19 ºC: 90% 7. Si la humedad absoluta del aire es de 23 g/m 3 y el déficit de saturación es del 20%, indicad, con ayuda del diagrama: a) La temperatura aproximada del termómetro seco y la del termómetro húmedo de un psicrómetro; b) El valor mínimo que podría alcanzar la temperatura del aire sin que apareciera condensación; c) Cantidad aproximada de vapor de agua que se condensaría si, en las citadas condiciones de humedad, la temperatura bajase a 11 ºC. Resultado: a) Ta = 29 ºC , Tw = 26 ºC b) T. punto de r ocío: 25 ºC c) 13 g/m 3 8. Una masa de aire se encuentra a una temperatura de 28ºC y presenta una humedad relativa del 51%. La relación entre la presión saturante del vapor de agua (es) y la temperatura (t), expresando es en mbar y t en ºC, es:
æ 17 , 27 ∙ t ö
çç
÷÷
è t + 237 , 28 ø
e s = 6,108 × e Calculad: a) El déficit de presión vapor es­ea expresado en mbar . b) La temperatura en el punto de rocío
Resultado: æ 17 , 27 ∙ 28 ö
çç
÷÷
è 28 + 237 , 28 ø
e s = 6 , 108 × e = 37 , 79 mbar a) ( 100 ­ 51) ∙37,79 / 100 = 18,52 mbar b) ea = 0,51 ∙ 37,79 = 19,28 mbar ( 17,2674 ∙ t ) / ( t + 237,28 ) = ln ( 19,28 /6,108 ) ; t = 16,92 ºC 50 50 50 90 90 45 45 80
80
40 40 35 30 50 25 40 20 20 60 30 30 50 25 40 20 20 30 30 15 15 20 10 Humedad absoluta (g/m 3 ) 70 35 60 30 40 70 Humedad Relativa (%) Humedad absoluta (g/m 3 ) 40 20 10 10 10 10
5 0 10 5 0 0 0 10 20 30 Humedad Relativa (%) 50 40 0 0 Temperatura (ºC) 10 20 30 40 Temperatura (ºC) Pr oblema 6 Pr oblema 7 9. Calcula la humedad absoluta de una masa de aire que presenta una humedad relativa del 35 % y se encuentra a una temperatura de 35ºC. La fórmula que relaciona la humedad absoluta (r con la presión parcial de vapor de agua (e) y la temperatura (T) es:
r = 216,45 (e / T) T en grados K, r en g/m 3 , e en mbar y la relación entre la tensión de vapor saturado (es) y la temperatura (t)
æ 17 , 27 • t ö
çç
÷÷
è t + 237 , 28 ø
e s = 6 , 108 • e t en ºC Resultado: æ 17 ,27 ∙ 35 ö
çç
÷÷
è 35 + 237 , 28 ø
e s = 6 , 108 • e = 56 , 94 mbar ea = 56,94 ∙ 0,35 = 19,93 mbar r = 216,45 (19,93 / 308,15 ) = 14 g/m 3 es en mbar 10. Si la temperatura del aire es de 30 ºC y la temperatura del punto de rocío 15 ºC, cuál será: a) el déficit de saturación, b) la humedad relativa (Puedes utilizar las relaciones de la pregunta anterior). Resultado: æ 17 , 27 ∙ 15 ö
çç
÷÷
è 15 + 237 , 28 ø
e a = 6 , 108 • e æ 17 , 27 ∙ 30 ö
çç 30 + 237 , 28 ÷÷
è
ø
e s = 6 , 108 • e = 17 , 05 mbar = 42 , 42 mbar a) es – ea = 42,42 – 17,05 = 25,37 mbar b) HR % = (17,05/42,42) ∙ 100 = 40,2 % 11. La temperatura del termómetro húmedo de un psicrómetro no ventilado es th = 36.9 ºC, y la del termómetro seco ts = 40 ºC, la constante del psicrómetro es a = 0.0008 ºC ­1 y la presión atmosférica P = 1000 mbar. La ecuación que determina la presión de vapor es: ea = es(th) ­ a.P.(ts ­ th) donde: es(th) es la presión de saturación en milibares a la temperatura del termómetro húmedo. Calculad la humedad relativa en % en el momento de la medida, sabiendo que la relación entre la tensión de vapor saturado (es) y la temperatura (t) es: æ 17 , 27 • t ö
çç
÷÷
è t + 237 , 28 ø
e s = 6 , 108 • e expresando es en mbar y t en ºC.
Resultado: æ 17 , 27 ∙ 36 , 9 ö
çç 36 , 9 + 237 , 28 ÷÷
è
ø
e s ( th ) = 6 , 108 • e = 62 , 4 mbar ea = 62,4 – 0.0008 ∙ 1000 ∙ (40 – 36,9) = 59,9 mbar æ 17 , 27 ∙ 40 ö
çç
÷÷
è 40 + 237 , 28 ø
e s = 6 , 108 • e = 73 , 7 mbar HR = (59.9 / 73.7) ∙ 100 = 81.3 % 12. En una determinada localidad durante el periodo 1980­1999 se han registrado las siguientes precipitaciones mensuales durante el mes de Junio: 70­61­57­21­58­66­17­72­51­40­28­33­64­97­68­80­71­ 25­60­77. a) Calcula la precipitación que se espera sea superada el 50% de los años. b) Calcula la probabilidad de que la precipitación supere 50 mm Resultado: Orden (n): 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 P (mm): 17 21 25 28 33 40 51 57 58 60 61 64 66 68 70 71 72 77 80 97 a) p = n /(m+1) = 0,5; n = 21 ∙ 0,5 = 10,5 P = 60,5 mm b) n ≈ 6.91 ; p = 1 ­ (6.91/21) = 0.67 → 67 %
13. En una localidad, se han registrado, durante los últimos 10 años, las fechas de la primera y última helada: Determinad: a) El período medio libre de heladas b) Probabilidad de que ocurra una helada primaveral después del 30 de Marzo. Año 1987 Fecha de la 1/11 primera helada Fecha de la 27/2 última helada 1988 1989 1990 1991 1992 1993 1994 1995 1996 27/10 14/11 29/12 3/11 20/10 14/11 27/10 3/11 7/11 14/2 12/3 7/4 27/4 22/4 14/2 20/3 17/4 12/3 Resultado: Orden (n): 1 2 3 4 5 6 7 8 9 10 Pr. h. 20/10 27/10 27/10 1/11 3/11 3/11 7/11 14/11 14/11 29/12 Últ. h. 27/4 22/4 17/4 7/4 20/3 12/3 12/3 27/2 14/2 14/2 a) p = n /(m+1) = 0,5; n = 11 ∙ 0,5 = 5,5 per iodo medio de heladas desde 3/11 hasta 16/3 → libr e de heladas desde 17/3 hasta 2/11 b) n ≈ 4,4 ; p = 4,4/11 = 0.4 → 40 % 14. Suponed que la evolución diaria de las temperaturas del suelo puede ser aproximada por la función senoidal: ( - z T ( z , t ) = T m + A o e p ) æ
K t sen ç
2 p
p ö÷
t - z ç t
K t ÷ø
è
Donde: T(z, t) (ºC) es la temperatura a la profundidad z(cm) y en el tiempo t(horas), Tm (ºC) es la temperatura media diaria del suelo (la misma a todas las profundidades), Ao (ºC) es la semioscilación térmica diaria de la superficie del suelo, t es el periodo o tiempo necesario para completar un ciclo de la onda y K(cm 2 /h) es la difusividad térmica del suelo. En un suelo en que K=12,5 cm 2 /h, la temperatura máxima de la superficie del suelo es 33 ºC y la temperatura mínima en la superficie del suelo es 3 ºC. Emplead la ecuación para estimar la temperatura a 40 cm de profundidad 5 horas después de que se alcanzase la temperatura máxima en la superficie del suelo. Resultado: t = 24 hor as, por ser un ciclo diar io; en la super ficie z= 0 Tm = (33+3)/2=18 ºC Ao = (33 – 3)/2 = 15 ºC La temper atur a máxima en la super ficie se alcanzar á cuando sen(...) = 1 ; es decir cuando el ángulo sea p/2 ( 2 p / t ) ∙ t = p / 2; t = 6 h 5 hor as después t = 11 h ( -40 T ( z , t ) = 18 + 15 ∙ e p
) 12 . 5 ∙ 24 æ 2 p
ö
p
÷ = 17 . 8 º C ∙ sen ç 11 - 40 ç 24 ÷
12 . 5 ∙ 24 è
ø
15. Calculad la precipitación media en el área de la figura según el método Thiessen, siendo las superficies asignadas a cada pluviómetro dentro del área problema las siguientes en km 2 : Pluviómetro A B C D E F G H I J K Pluviometría (mm) 7 19 15 28 27 45 16 30 52 20 18 Km 2 17 95 130 0 125 109 10 119 102 15 0
Resultado: P = (7∙17+19∙95+15∙130+27∙125+45∙109+16∙10+30∙119+52∙102+15∙20) / (17+95+130+125+109+10+119+102+15) = 29.76 mm 16. Un lisímetro de pesada, cilíndrico, de 2 m de diámetro y 1 m de profundidad se utiliza para medir la evapotranspiración diaria. Si un día hubo una precipitación de 40 mm, se midió un drenaje de 16 litros y hubo un incremento de peso de 88 kg. ¿Cuál fue la evapotranspiración ese día en mm? Resultado: S = 3,14 m 2 ET = P – Dq – D = 40 – (88 + 16) / 3,14 = 6,9 mm/día 17. Calcula por el método FAO Penman­Monteith la evapotranspiración de referencia diaria media en mm/día del mes de julio de una determinada localidad situada a una latitud de 38ºN y a una altitud de 120 m. Los datos medios de un mes en esta localidad son: Temperatura media de máximas = 34.6 ºC Temperatura media de mínimas = 20.8 ºC Radiación solar = 26.46 MJ m ­2 día ­1 Albedo = 0,23 Radiación neta de onda larga = 5.79 MJ m ­2 día ­1 G = 0,25 MJ m ­2 día ­1 Presión de vapor de agua media = 1,388 kPa Velocidad del viento a 2 metros de altura (u2) = 1.69 m/s
D = 0,217 kPa/ºC; g = 0,0668 kPa/ºC La fórmula de FAO Penman­Monteith es la siguiente: ETo (mm/día) = 0 , 408 . D.( Rn - G ) + g .{ 900 /( T + 273 )}. u 2 .( e s - e a ) D + g .( 1 + 0 , 34 . u 2 ) Donde: Rn y G vienen expresados en MJ m ­2 día ­1 , T en ºC, la velocidad del viento (u2) en m/s, el déficit de presión de vapor en kPa y D y g en kPa/ºC. Para el cálculo del déficit de presión de vapor puedes basarte en la fórmula que relaciona la presión saturante de vapor de agua (es) expresado en kPa con la temperatura (t) en ºC: es = 0,6108.e (17,27 ∙ t / (t + 237,28)) Resultado: Rn = Rnc – Rnl = (1 ­ 0.23) ∙ 26.46 – 5.79 = 14.58 MJ m ­2 día ­1 T = (20.8 + 34.6) / 2 = 27.7 ºC æ 17 , 27 ∙ 34 , 6 ö
çç
÷÷
è 34 , 6 + 237 , 28 ø
e s T max = 0 , 6108 × e æ 17 , 27 ∙ 20 , 8 ö
çç 20 , 8 + 237 , 28 ÷÷
è
ø
e s T min = 0 , 6108 × e es = (5,50 + 2,46) / 2 = 3,98 kPa es – ea = 3,98 – 1,388 = 2,592
= 5 , 50 kPa = 2 , 46 kPa ETo =
0 ,408 ∙ 0 , 217 ∙ ( 14 , 58 - 0 , 25 ) + 0 , 0668 ∙ { 900 /( 27 , 7 + 273 ) }∙ 1 , 69 ∙ 2 , 592 = 6,66 mm/día 0 , 217 + 0 , 0668 ∙ ( 1 + 0 , 34 ∙ 1 , 69 ) 18.­ Una masa de aire presenta una humedad relativa del 45% y la temperatura mínima que puede alcanzar sin que haya condensación es de 13 ºC. La relación entre la presión del vapor de agua en saturación (es) y la temperatura (t), expresando es en mbar y t en ºC, es:
æ 17 , 27 ∙ t ö
çç
÷÷
è t + 237 , 3 ø
e s = 6,108 × e La fórmula que relaciona la humedad absoluta (rv con la presión parcial de vapor de agua (ea) y la temperatura (T) es: ea = 4,62∙10-3 ∙rv ∙T donde: T en ºK, rv en g/m 3 , ea en mbar Calculad: a) El déficit de presión vapor (es ­ ea ), expresado en kPa . b) La temperatura del aire c) Considerando las condiciones anteriores, si la temperatura desciende hasta 7ºC, ¿Aproximadamente, qué cantidad de vapor de agua expresado en g/m 3 condensará? Resultado: a) ea es igual a la presión de vapor en satur ación a la temper atur a del punto de r ocío (t pr = 13ºC ) æ 17 , 27 ∙ 13 ö
çç 13 + 237 , 3 ÷÷
è
ø
e a = 6,108 × e = 14 , 98 mbar = 1 , 498 kPa es = (100 ∙ ea) / HR = 149,8 / 45 = 3,329 kPa es – ea = 3,329 – 1,498 = 1,831 kPa b)
æ 17 , 27 ∙ t ö
çç t + 237 , 3 ÷÷
è
ø
æ 33, 29 ö 17 , 27 ∙ t ÷=
è 6 , 108 ø t + 237 , 3 33 ,29 = 6,108 × e ln ç
1,696 t + 1,696 ∙ 237,3 = 17,27 t t = 402,46 / 15,574 = 25,84 ºC c) rv = ea / (4,62∙10 ­3 T) = 14,98 / (4,62∙10 ­3 ∙ (273,15 + 13)) = 11,33 g/m 3 æ 17 , 27 ∙ 7 ö
ç
÷
è 7 + 237 , 3 ø
e a = 6,108 × e = 10 , 02 mbar rv = ea / (4,62∙10 ­3 T) = 10,02 / (4,62∙10 ­3 ∙ (273,15 + 7)) = 7,74 g/m 3 Se condensar á 11,33 – 7,74 = 3,59 g/m 3 19.­ Un centro de investigación agraria tiene una estación agrometeorológica en cuyo interior existen entre otros instrumentos un lisímetro de pesada de forma cúbica de 1,5 m de lado, un pluviómetro con una superficie captadora circular de 24 cm de diámetro, y un tanque evaporimétrico tipo A de 1,2 m de diámetro. Los instrumentos son leídos semanalmente. En dos pesadas consecutivas, en el lisímetro se obtuvo unos valores de 3000 y 2955 kg, y un drenaje de 22,5 L. Asimismo, durante el mismo periodo considerado, el pluviómetro recogió 1130 cm 3 . A partir de estos datos, determinad: a) La precipitación en m 3 /ha durante el periodo medido. b) La evapotranspiración media diaria en mm producida durante el periodo medido. c) La variación de altura en cm producida en el tanque evaporimétrico durante el periodo medido, considerando que el coeficiente del tanque (Kp) es igual a 0,85.
Resultado: a) Super ficie captador a del pluviómetr o: S = 12 2 ∙ 3,14 = 452,39 cm 2 Altur a de lluvia: H = V/S = 1130 / 452,39 = 2,50 cm 0,025 m ∙ 10000 m 2 /ha = 250 m 3 /ha b) Dq = 2955 ­ 3000 = ­ 45 kg = ­ 45 L D + Dq = 22.5 ­ 45 = ­ 22.5 L Super ficie del lisímetr o = 1,5 ∙ 1,5 = 2,25 m 2 ETo = P – (D + Dq) = 25 + 22,5/2,25 = 35 mm/semana ETo = 35/7 = 5 mm/día c) ETo = Ep * Kp; Ep = 35 / 0.85 = 41,18 mm Descender ía 41.18 mm debido a la evapor ación, per o como hubo un apor te de agua debido a la lluvia de 25 mm, el descenso neto ser á: 41.18 – 25 = 16.18 mm = 1.62 cm 20.­ Un centro de investigación agraria posee un lisímetro de 2 m de ancho, 2,6 m de largo y 1,5 m de profundidad, situado en una parcela experimental. Se dispone de los siguientes datos: Humedad de suelo (% en volumen): ­ 1 de junio: 21% ­ 1 de julio: 15% Precipitación: ­ 9 de junio: 19 mm ­ 24 de junio: 13 mm Volumen de drenaje recogido en el desagüe del lisímetro: ­ 10 de junio: 107 L ­ 25 de junio: 71 L Riego aplicado a toda la parcela: ­ 7 y 21 de junio 300 m 3 /ha en cada fecha. Calculad la evapotranspiración del mes de junio en mm/día a partir de los datos anteriores. Resultado: Super ficie del lisímetr o = 2 ∙2,6 = 5,2 m 2 Volumen del lisímetr o = 5,2 ∙ 1,5 = 7,8 m 3
Dq = ((15 – 21)/100) ∙ 7,8 = ­ 0,468 m 3 = ­ 468 L D = 107 + 71 = 178 L R = 600 m 3 /ha = 60 mm P = 19 + 13 = 32 mm ETo = P + R – (D + Dq) = 32 + 60 – (178 – 468) / 5,2 = 147,77 mm/mes ETo = 147,77/30 = 4,93 mm/día 21.­ Los valores de la temperatura media del mes de mayo durante los últimos 18 años medidos en dos estaciones agrometeorológicas cercanas (A y B) son los siguientes: A B 1988 17,5 18 1989 15,5 17,8 1990 16 17 1991 18 18 1992 18 19,2 1993 17,5 18 1994 16,7 17 1995 16,6 17 1996 18,5 19,5 1997 17,7 18,1 1998 15 16 1999 15,7 16 2000 16 18 2001 15,5 17,5 2002 14,5 16 2003 16,3 17 2004 16 18,5 2005 15,8 18 a) Comprobad si ambas series de temperaturas son homogéneas usando para ello el test de secuencias, sabiendo que para que un registro de datos sea homogéneo el número de secuencias debe oscilar entre 7 y 12 (para una serie de 18 datos como es este caso).
b) Si una de las series no es homogénea, realizad un ajuste por comparación para homogeneizar dicha serie, teniendo en cuenta que la discontinuidad en dicha serie se da entre el año 1996 y el año 1997. Resultado: a) Temper atur a media en la estación A = 16,49 Temper atur a media en la estación B = 17,59 A 1988 17,5 + 1989 15,5 ­ 1990 16 ­ 1991 18 + 1992 18 + 1993 17,5 + 1994 16,7 + 1995 16,6 + 1996 18,5 + 1997 17,7 + 1998 15 ­ 1999 15,7 ­ 2000 16 ­ 2001 15,5 ­ 2002 14,5 ­ 2003 16,3 ­ 2004 16 ­ 2005 15,8 ­ 2002 16 ­ 2003 17 ­ 2004 18,5 + 2005 18 + Númer o de secuencias 4, como es inferior a 7 se sospecha que no es homogénea esta ser ie B 1988 18 + 1989 17,8 + 1990 17 ­ 1991 18 + 1992 19,2 + 1993 18 + 1994 17 ­ 1995 17 ­ 1996 19,5 + 1997 18,1 + 1998 16 ­ 1999 16 ­ 2000 18 + 2001 17,5 ­ Númer o de secuencias 9, como está compr endida entre 7 y 12 no se puede sospechar que no sea homogénea esta ser ie b) A B B­A A B B­A 1988 17,5 18 0,5 1989 15,5 17,8 2,3 1990 16 17 1 1991 18 18 0 1992 18 19,2 1,2 1993 17,5 18 0,5 1994 16,7 17 0,3 1995 16,6 17 0,4 1996 18,5 19,5 1 Media 1997 1998 1999 2000 2001 2002 2003 2004 2005 Media 17,7 18,1 0,4 15 16 1 15,7 16 0,3 16 18 2 15,5 17,5 2 14,5 16 1,5 16,3 17 0,7 16 18,5 2,5 15,8 18 2,2 1,4 0,8 Las condiciones anterior es a 1997 de la estación A er an 0,6 ºC más cálidas que a par tir de 1996 La ser ie A homogeneizada tendr á de temper atur a media 16,19 ºC: A 1988 16,9 + 1989 14,9 ­ 1990 15,4 ­ 1991 17,4 + 1992 17,4 + 1993 16,9 + 1994 16,1 ­ 1995 16 ­ 1996 17,9 + 1997 17,7 + 1998 15 ­ 1999 15,7 ­ 2000 16 ­ 2001 15,5 ­ 2002 14,5 ­ 2003 16,3 + 2004 16 ­ 2005 15,8 ­ Númer o de secuencias 8, que está compr endida entr e 7 y 12 22.­ En una determinada zona, las precipitaciones mensuales registradas durante el mes de octubre en el período 1985­2004 fueron las siguientes: 39 – 22 – 25 – 57 – 84 – 53 – 74 – 66 – 18 – 44 – 69 – 64 – 46 – 52 – 9 – 80 – 59 – 14 – 73 – 37. Calculad: a) La precipitación que se espera sea superada el 25% de los años. b) La precipitación que se espera no sea superada el 81 % de los años. c) La probabilidad que en ese mes la precipitación supere los 18 mm. d) La probabilidad que en ese mes la precipitación no supere los 75 mm. Resultado: Orden (n): 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 P (mm): 9 14 18 22 25 37 39 44 46 52 53 57 59 64 66 69 73 74 80 84 Pr ob.(x £ p) = n / 21 4,8 9,5 14,3 19 23,8 28,6 33,3 38,1 42,9 47,6 52,9 57,1 61,9 66,7 71,4 76,2 81 85,7 90,5 95,2
a) Pr ob(x > p) = 1 ­ Pr ob.(x £ p) = 1 – n/21 = 0,25 n = 15,75 p = 68,25 mm b) No sea… = 1 – sea…= 1 – Pr ob.(x > p) = 1 – (1 ­ Pr ob.(x £ p)) = Pr ob.(x £ p) = 0,81 = n/21 n = 17, 0 p = 73 mm c) Pr ob.(x > 18) = 1 ­ Pr ob.(x £ 18) = 1 – 3/21 = 0,857 = 85,7 % d) Pr ob.( x £ 75) = n/21 = 18,17/21 = 0,865 = 86,5 % 23.­ En el momento de mínima temperatura del aire de un día cualquiera, el termómetro húmedo de un psicrómetro mide 13 ºC y la humedad relativa es de un 80%. De igual forma, en el momento de máxima temperatura de ese mismo día, dicho termómetro húmedo mide 19 ºC y la humedad relativa es de un 30%. Conociendo estos datos y con ayuda del gráfico siguiente, indicad: a) Los valores de temperatura del aire (máxima y mínima) en los dos momentos del día indicados. b) El déficit de presión de vapor en kPa en el momento de mínima temperatura. c) La presión de vapor en saturación media en kPa de ese período. d) La temperatura de rocío que corresponde con el valor de máxima temperatura del aire. e) ¿Habrá habido condensación de vapor de agua a lo largo de ese día? ¿Por qué? Resultado: a) T mín = 15 ºC Tmáx = 31,3 ºC b) a 15 ºC es = 17 hPa ea = 13,7 hPa es ­ ea = 3,3 hPa = 0,33 kPa c) a 15 ºC es = 17 hPa a 31,3 ºC es = 45,7 hPa es = (45,7 + 17 ) / 2 = 31,4 hPa = 3,14 kPa d) Tp.r . = 11,5 ºC e) No, por que la temper atur a mínima que se ha alcanzado ( 15 ºC) es super ior a la temper atur a del punto de r ocío (11,5 ºC) 50 40 50 40 30 30 20
20 10 10 0 0 5 10 15 20 25 30 Temperatura (ºC) 35 40 45 50 Humedad Relativa (%) Presión de vapor (hPa) 60 24. En una localidad, se han registrado, en el período 1981­2000, las siguientes fechas de la primera y última helada: Año 81/82 Fecha de la 5/12 primera helada Fecha de la 11/2 última helada 82/83 83/84 84/85 85/86 86/87 87/88 88/89 89/90 90/91 20/12 ­ 4/11 11/11 7/11 3/12 8/12 28/10 15/12 25/2 ­ 6/2 30/1 5/2 14/3 14/4 3/3 7/3 Año 91/92 Fecha de la 13/12 primera helada Fecha de la 17/2 última helada 92/93 93/94 94/95 95/96 96/97 97/98 98/99 99/00 00/01 24/12 1/11 28/12 3/1 21/12 3/12 19/11 18/12 5/11 7/4 21/4 22/2 18/3 8/2 16/2 12/3 15/1 1/3 Determinad: a) El período medio de heladas. b) Probabilidad de que ocurra una helada después del 15 de Febrero. c) Probabilidad de que haya una helada antes del 15 de Noviembre. d) Fecha a partir de la cual se espera que la probabilidad de heladas sea inferior o igual al 20%. e) Fecha hasta la que la probabilidad de que ocurra una helada es inferior o igual al 10%. Resultado: Suponemos independencia entre las fechas de pr imer a y última helada. Or denamos la fecha de pr imer a helada en sentido ascendente y de la última en sentido descendente. Orden (n): 1 2 3 4 5 6 7 8 9 10 Pr. h. 28/10 1/11 4/11 5/11 7/11 11/11 19/11 3/12 3/12 5/12 Últ. h. 21/4 14/4 7/4 18/3 14/3 12/3 7/3 3/3 1/3 25/2 Orden (n): 11 12 13 14 15 16 17 18 19 20 Pr. h. 8/12 13/12 15/12 18/12 20/12 21/12 24/12 28/12 3/1 ­ Últ. h. 22/2 17/2 16/2 11/2 8/2 6/2 5/2 30/1 15/1 ­ a) P = n /(m+1) = 0,5; n = 21 ∙ 0,5 = 10,5 per iodo medio de heladas desde 7/12 hasta 24/2 → libr e de heladas desde 25/2 hasta 6/12. b) Última helada: P(x>15/2)=P(x≥16/2)= n /(m+1)=13/21=0.619 del 62% c) Primer a helada: P(x<15/11)=P(x£14/11)= n /(m+1)=6,375/21=0.30 d) Última helada: P(x≥X)=0,2= n /(m+1); n=0,2 ∙ 21=4,2 del 30% el 17 de Marzo c) Primer a helada: P(x£X)=0,1= n /(m+1); n=0,1 ∙ 21=2,1 el 1 de Noviembr e