Tema Nº 1 Introducciòn a la Investigación operativa
Anuncio
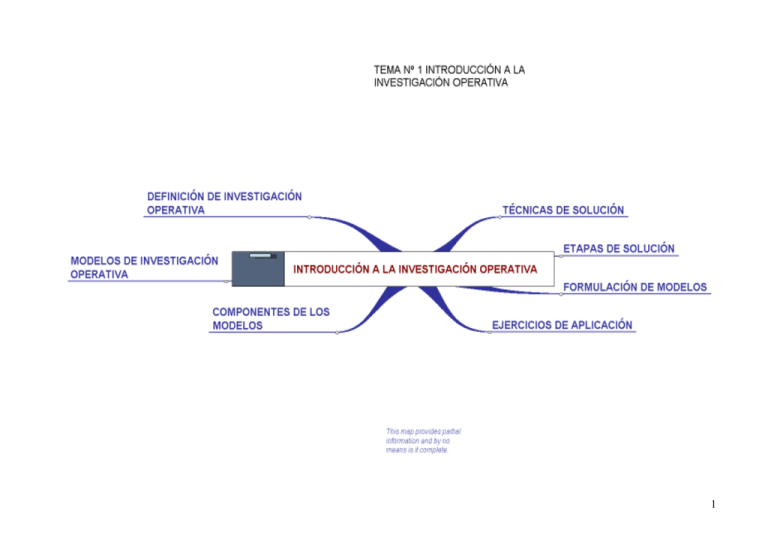
1 Unidad Nº 1 Introducción a la Investigación operativa Competencia: el estudiante debe tener el marco teórico general de la Investigación Operativa a través de las definiciones conceptos básicos y procedimientos sobre los modelos de programación en cuanto a sus fases de análisis de la investigación de operaciones de los diferentes modelos de programación lineal. Descripción general de la unidad.- la unidad I trata sobre la definición y concepto sobre la investigación de operaciones y la descripción de las diferentes fases sobre el análisis de la investigación de operaciones de los diferentes modelos de programación lineal. Introducción.La Investigación Operativa surge durante la 2ª Guerra mundial, principalmente en la toma de decisiones respecto de la utilización de los materiales bélicos .Al final de la misma se extiende al sector civil en cuanto a la eficiencia y la productividad. Actualmente la Investigación Operativa constituye la herramienta fundamental en la toma de decisiones respecto a cualquier actividad económica limitado por los escasos recursos disponibles y/o elevar la eficiencia de algunos servicios, considerando además factores intangibles como el comportamiento psicológico de las personas. Definición.La Investigación Operativa es una de las ramas de las Matemáticas, consistente en el uso de Modelos Matemáticos, estadísticos y Algoritmos en el proceso de la toma de decisiones. Generalmente trata el estudio de complejos sistemas reales con la finalidad de optimizar (maximizar o minizar) o de mejorar la eficiencia de los mismos. La investigación operativa permite el análisis de la toma de decisiones teniendo en cuenta los escasos recursos, para determinar como se puede optimizar un objetivo definido la maximización de los beneficios o la minimización de los costos. Modelos de Investigaciones de Operaciones.Los Modelos de Investigación depuraciones tienen tres componentes. 1) Las alternativas o variables,2) Objetivo 3)y Las restricciones. Los mismos que permiten organizar para: a) Maximizar o minimizar la función objetivo, b) Sujeto a restricciones o condiciones Se dice que un Modelo tiene solución factible si satisface todas las restricciones y es óptima si produce el mejor valor (Máximo o Mínimo) para la función objetivo Técnicas de solución de los modelos de Investigación Operativa.De acuerdo a la naturaleza de los modelos se tiene diferentes técnicas de solución, entre ellas tenemos: 1) Programación lineal.Se utiliza esta técnica cuando los modelos tienen las funciones objetivos y las restricciones estrictamente lineales (las variables de la función como de las restricciones deben tener potencia unitaria) 2) Programación entera.Se utiliza cuando las variables toman valores enteros 3) Programación Dinámica.2 Se utiliza cuando el modelo original se puede descomponer en subproblemas o submodelos más pequeños. 4) Programación de Red.Se utiliza cuando el problema o modelo se puede construir o modelar como una red. 5) Programación No Lineal Se utiliza cuando el modelo tiene funciones no lineales. Nota.Generalmente estas técnicas de Investigación no dan soluciones únicas o cerradas, tal como se obtiene al aplicar fórmulas, por lo que se debe recurrir a: Algoritmos Son reglas fijas de cómputo que se utilizan en forma iterativa al problema, donde cada iteración obtiene una solución cada vez más cercana a la óptima (para ello es necesario recurrir algún paquete). Cuando los modelos son demasiados complejos, siendo imposible resolverlos mediante algoritmos de optimización, se deberá recurrir a reglas simples de criterio. Dentro los modelos de Investigación operativa tenemos dos modelos especiales: 1) Modelos de Colas Utilizados principalmente en problemas de líneas de espera que buscan a la mayor eficiencia del servicio y basados en modelos probabilísticas, sujetos a hipótesis especificas, limitando el alcance de la aplicación. 2) Modelos de Simulación.Por diferentes factores se suele recurrir a la simulación de los problemas de líneas de espera principalmente, por lo tanto estima las medidas de eficiencia, siendo esta mas flexible que la anterior. Necesidad de los Modelos.En forma general Modelo es la representación simple, mediante la abstracción, de cualquier aspecto de las ciencias del mundo real, se logra la simplificación del mundo real al mundo “supuesto” utilizando variables que permitan cuantificar el problema y por ende resolverlos. Por Ej. se tiene una empresa manufacturera que produce una variedad de empaques de de plástico para PC. Cuando se emite una orden de producción al departamento de producción, se adquieren las materias primas necesarias en los almacenes de la empresa o se compran de proveedora externos .una vez terminado el lote de producción, el depto. De ventas se hace cargo de distribuir el producto entre los consumidores. Un problema fundamental sería determinar el tamaño del lote, y como se podría representar en el modelo. Para determinar las variables que influyen de manera directa en el nivel de producción, será necesario clasificar los departamentos de la empresa: 1.-Departamento de producción.-que está en función de la capacidad de producción expresada en función de las horas máquina y mano de obra disponible, inventario en proceso y normas de control de calidad 2.-Departamento de materiales.-que está en función del stock disponible de materias primas, programas de entrega de sus proveedores y limitaciones de almacenamiento 3-Departamento de ventas.- que está en función del pronóstico de ventas, capacidad de las instalaciones de distribución, eficacia de la campaña publicitaria y efecto de la competencia Como se podrá ver existen varias variables explícitas, en este caso el de producción, de materiales y el de ventas las mismas que a su vez están en función de otras variables implícitas, por lo tanto es muy 3 complejo establecer las relaciones existentes entre estas variables y el nivel de producción, para solucionar éste problema se puede aproximar al sistema real mediante la utilización de otras variables llamadas dominantes como ser: 1.-Tasa de producción.-la misma que implica variables como la capacidad de producción, las normas de control de calidad y la disponibilidad de las materias primas 2.-Tasa de consumo.- la misma que está determinada por las variables asociadas al depto de ventas. A partir de estas tasas se puede establecer medidas de exceso o carencia de inventario. El modelo sintetizado se puede definir de modo que equilibre los costos contrapuestos de exceso y de carencia de inventario, es decir que minimice el costo del inventario. FASES DEL ANALISIS DE INVESTIGACION DE OPERACIONES La construcción de los modelos de investigación operativa requiere de la ciencia como del arte del investigador, de la ciencia porque utiliza técnicas matemáticas y del arte porque requiere habilidad destreza experiencia y juicio. Para ello se sugiere seguir los lineamientos generales para implementar la investigación de operaciones: 1) La definición del problema 2) La construcción del modelo 3) La solución del modelo 4) La validación del modelo 5) La Implementación del modelo. 1) Definición del modelo o planteamiento del problema.Se debe delimitar el alcance del problema que se investiga interdisciplinariamente entre todo el equipo de investigación, la misma que comprende específicamente en: a) La descripción de las alternativas de decisión que generalmente se traduce en las entrada variables de b) La determinación del objetivo de estudio que se traduce como función matemática, la misma que se optimizará (Maximizando o Minimizando) c) La especificación de las limitaciones en el que el modelo funciona, traduciéndose en restricciones explícitas (disponibilidad de recursos) como implícitas (de no negatividad de las variables y/o el carácter de enteros de las mismas. 2) Construcción del modelo Representar la definición del problema como relación matemática o función matemática objetivo. Si resultan modelos matemáticos “normales” (programación Lineal), se puede llegar a soluciones utilizando los diferentes algoritmos disponibles. Si resultan demasiados complejos, se debe simplificar y utilizar un método heurístico o recurrir al uso de la simulación si se desea aproximar, o en algunos casos combinar modelos matemáticos de simulación con los heurísticos. 3) La solución del modelo.Se utilizan los algoritmos de optimización, debiendo ejecutarse un análisis de sensibilidad, principalmente cuando no se pueden determinar con exactitud los parámetros del modelo. 4) Validación del modelo.- 4 Para determinar si el modelo en cuestión es el adecuado, éste se debe comprobar principalmente cuando se desea predecir el comportamiento del sistema en cuestión, de manera que no se produzcan”sorpresas”,debiendo comprobar con datos históricos, siendo válido si reproduce el funcionamiento con el pasado .Cuando el sistema es nuevo y no se cuenta con datos históricos, se sugiere recurrir la simulación. 5) Implementación del modelo La implantación de la solución del modelo se entiende la instrucción de la operación de los resultados obtenidos en el modelo, dichas instrucciones deben ser emitidas de manera comprensiva para el personal que administran el sistema. 5