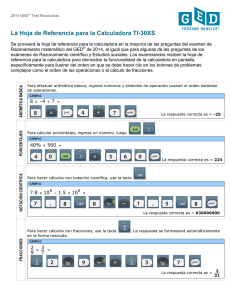
Antología EMAT1
Anuncio

Ma. Guadalupe Flores Barrera Andrés Rivera Díaz Contenido EMAT-Hidalgo i ii 1 Introducción Organización de la Antología EMAT-Hidalgo Programación Primer Grado, EMAT-Hidalgo Septiembre 4 5 7 9 Un paseo corto por una hoja de cálculo (28) Lectura y escritura de números (24) y Virus y antivirus (25) Fracciones equivalentes (115-116) Comparar fracciones (Actividad didáctica) Octubre 11 13 15 16 Generando secuencias de Números (38-39) Propiedades de la simetría axial, (58-59) Transformaciones con Simetría axial (Actividad didáctica) Comparando Secuencias (40-41) Noviembre 18 20 21 23 Fracciones equivalentes (116-117) Multiplicación y estimación (34) Construcción del paralelogramo (50-51) Medición de perímetros, áreas y ángulos (60-61) Diciembre 25 27 Idea de variación (rectángulos) (66-67) Variación proporcional 1 (53-54) Enero 29 30 32 33 Transformaciones en un solo paso (39) Ecuaciones 1 (61-62) ¿Qué fracciones faltan? (50) Descuentos y más descuentos (51-52) Febrero 35 39 43 45 Unidad 4. Polígonos regulares (43-46) Cálculo de Áreas (Actividad didáctica) Análisis de textos (142-143) Unidad 16. Azar y probabilidad (138-139) Marzo y Abril 47 49 51 52 53 56 Variación lineal 1 (77-78) ¡Se descompuso la tecla de la raíz cuadrada! (42-43) Punto equidistante (Actividad didáctica) Circunferencia y círculo (Actividad didáctica) Relación entre la longitud de una circunferencia y el área del círculo (68-70) Unidad 18. Círculos (156-160) 61 63 66 68 Mayo ¿Cómo sumamos números con signo? (53-54) Sumas y restas de números con signo (55-57) Adivina qué está pasando (147-148) ¿Por dónde saldrá? (149-151) 71 72 73 74 75 Junio Variación Reciproca I (Actividad didáctica) Variación Reciproca II (Actividad didáctica) Media, Mediana y Moda (Actividad didáctica) Jugando con las Calificaciones (Actividad didáctica) Bibliografía Introducción Las Tecnologías de la Información y Comunicación (TIC) suponen un revolucionario avance en nuestra sociedad. Presenciamos a una era de cambio y de modificaciones constantes que influyen significativamente en nuestras vidas. Mantenernos expectantes o tomar las riendas de emergentes procesos de cambio que nos pueden ayudar a construir un mundo sin barreras, un mundo mejor, es una elección a realizar de forma particular por cada uno de nosotros. En el ámbito educativo las TIC pueden suponer una importantísima ayuda como medio de acceder al currículum, así como también favorecer los aprendizajes escolares, particularmente de las matemáticas, como un reforzador didáctico, un medio para la enseñanza individualizada y, una herramienta fundamental de trabajo para el profesor. En definitiva pudiéramos preguntarnos, ¿Qué aspectos caracterizan a las TIC que las hacen tan especial en la educación matemática? Una reflexión alrededor de esta pregunta nos podría conducir a definir un grupo de aspectos que lo podrían caracterizar: 1. Aprendizaje continuo, por parte del alumno y del profesor, pues éste tendrá que estar actualizado para planificar con éxito las tareas docentes que realizarán los estudiantes. 2. Las TIC no solo pueden ser objeto de estudio sino que éstas deben pasar a ser herramienta indispensable para el alumno, tienen que ser integradas al entorno educativo. 3. Garantiza el desarrollo de una enseñanza significativa y facilita de antemano una educación integral. 4. Dinamiza el papel del profesor y del alumno, este último, de sujeto pasivo dentro del proceso pasa a ser protagonista del mismo junto al profesor, el cual tendrá como función rectora la orientación en el uso de las herramientas tecnológicas que sean utilizadas en el proceso. 5. Humaniza el trabajo de los profesores, pues ellos desarrollarán sus actividades con el apoyo de las tecnologías, economizando tiempo y energía. Además de estas ventajas que nos proporcionan las Tecnologías Educativas en el proceso de enseñanza, es bueno destacar que también permiten lograr una mejor interdisciplinaridad, o sea podemos relacionar el contenido matemático con el de otras asignaturas que contribuyan a una formación más eficiente y de carácter integral de nuestros estudiantes hidalguenses. Por lo anterior, la Dirección General de Educación Básica del Estado de Hidalgo, ha implementado el proyecto: Enseñanza de las Matemáticas con Tecnología, propuesta Hidalgo (EMAT-Hidalgo) a través de la Coordinación Estatal de los profesores: Ma. Guadalupe Flores Barrera y Andrés Rivera Díaz, quienes imparten un curso-taller programado, un día al mes, durante el ciclo escolar, al equipo de Coordinadores de las Zonas Escolares del Estado, de cada modalidad de Educación Secundaria, para que a la vez ellos lo multipliquen con sus profesores que imparten matemáticas de sus zonas correspondientes, en un día al mes también. I Las reuniones mensuales son un espacio de formación y actualización docente para el intercambio de experiencias, metodologías y conocimientos sobre las cuatro herramientas tecnológicas: Hoja electrónica de Cálculo, Calculadora TI-92, Geometría Dinámica y Programación computacional, las cuales son propuestas originales de la Subsecretaría de Educación Básica y Normal de la Secretaría de Educación Pública (SEP), en colaboración con el Instituto Latinoamericano de la Comunicación Educativa (ILCE). Como producto de ello se ha diseñado y compilado una Antología EMAT-Hidalgo, para cada grado escolar de educación secundaria. Por último, sabedores de que contamos con una comunidad educativa comprometida, aplicaremos esta Antología de Primer Grado, EMAT-Hidalgo, por el bienestar de nuestros alumnos hidalguenses. Mtro. Pablo Moreno Calva Director General de Educación Básica SEP, Estado de Hidalgo II Organización de la Antología EMAT-Hidalgo PRESENTACIÓN La Antología Enseñanza de las Matemáticas con Tecnología para la Educación Secundaria, Propuesta Hidalgo (EMAT-Hidalgo), es una compilación y diseño de actividades didácticas que contemplan el uso de cuatro piezas de tecnología estrechamente relacionadas, cada una con las áreas específicas de la geometría, el álgebra, la aritmética, la resolución de problemas y la modelación matemática. La Antología cumple, en forma paralela, con los planes y programas de estudio vigentes de matemáticas, para las modalidades de Educación Secundaria (General, Técnica y Telesecundaria). En la mayoría de las actividades seleccionadas, la construcción y el uso de estas cuatro piezas de tecnología cuentan con un sustento teórico y/o empírico, respectivamente, que respaldan su valor como herramientas mediadoras del aprendizaje en lo cognitivo y en lo epistemológico. La propuesta Hidalgo, es trabajar una sesión a la semana en el aula de medios o espacio asignado con equipos de cómputo, complementando las sesiones previas en el salón de clase. Esto implica que desde el inicio de curso escolar, los directivos deben elaborar los horarios, asignando en forma explícita, la sesión EMAT-Hidalgo a cada grupo. En la Antología, se incluye el uso de software de geometría dinámica para temas de geometría euclidiana; la calculadora TI-92 para la introducción a la sintaxis algebraica y a la resolución de problemas; el software de LOGO, lenguaje de programación con representación geométrica, al igual que la hoja electrónica de cálculo, para la enseñanza del álgebra, la resolución de problemas aritmético-algebraicos, y temas de probabilidad y de tratamiento de la información. En el espacio para desarrollar el proyecto EMAT-Hidalgo, el profesor guía a los estudiantes en su trabajo con el ambiente computacional y con las hojas de actividades didácticas programadas semanalmente en la Antología. Con las actividades se pretende que los alumnos alcancen cada vez mayores niveles de conceptualización matemática, para ello la programación de las actividades es de la siguiente manera: MES DE OCTUBRE Semana 1ra BLOQUE UNO 3. Representen sucesiones numéricas o con figuras a partir de una regla dada y viceversa. III Herramienta Actividad Hoja de cálculo Generando secuencias de Números (38‐39) Pág.. 11 En general, en el espacio EMAT-Hidalgo el profesor debe motivar a los alumnos a: ¾ Explorar. ¾ Formular y validar hipótesis. ¾ Expresar y debatir ideas. ¾ Aprender comenzando con el análisis de sus propios errores. Las sesiones EMAT-Hidalgo, se organizan a partir de actividades didácticas en las cuales los alumnos reflexionan sobre lo que han realizado con la computadora, y lo sintetizan para comunicarlo; por otro lado, estas actividades ya contestadas proporcionan información al profesor acerca de la comprensión que los alumnos tienen de los conceptos matemáticos involucrados. Finalmente, una reflexión: La educación es la base del progreso en cualquier parte del mundo y en la medida que el compromiso de los profesores se haga más expreso y se recupere la vocación profesional, podremos tener aspiraciones de superación sustentadas en hechos y no en sueños. Los autores: Ma. Guadalupe Flores Barrera y Andrés Rivera Díaz Coordinadores Estatales de EMAT-Hidalgo IV Programación Primer Grado EMAT-HIDALGO Sem. 1ra BLOQUE UNO 1. 2da 3ra 2. 4ta Sem. 1ra 2da MES DE SEPTIEMBRE Conozcan las características del sistema de numeración decimal (base, valor de posición, número de símbolos) y establezcan semejanzas o diferencias respecto a otros sistemas posicionales y no posicionales Herramienta Actividad Hoja de cálculo Un paseo corto por una hoja de cálculo (28) Calculadora Comparen y ordenen números fraccionarios y decimales mediante la búsqueda de expresiones equivalentes, la recta numérica, los productos cruzados u otros recursos Hoja de Cálculo Hoja de cálculo 5 7 9 MES DE OCTUBRE BLOQUE UNO Herramienta Actividad Generando secuencias de Números (38‐39) 4. Representen sucesiones numéricas o con figuras a partir de una regla dada y viceversa. Hoja de cálculo 4. Construyan figuras simétricas respecto de un eje e identifiquen cuáles son las propiedades de la figura original que se conservan. Geometría Dinámica 3ra Lectura y escritura de números (24) Virus y antivirus (25) Fracciones equivalentes (115‐116) Comparar fracciones (Actividad didáctica) Pág. 4 Propiedades de la simetría axial, (58‐59) Geometría Dinámica Transformaciones con Simetría axial Pág. 11 13 15 (Actividad didáctica) 4ta 5. Hoja de cálculo Sem. 1ra 1. 2da 2. 3ra 3. 4ta Resuelvan problemas de conteo con apoyo de representaciones gráficas. Comparando Secuencias (40‐41) 16 MES DE NOVIEMBRE BLOQUE DOS Resuelvan problemas que implican efectuar sumas, restas, multiplicaciones y divisiones con fracciones. Resuelvan problemas que implican efectuar multiplicaciones con números decimales. Justifiquen el significado de fórmulas geométricas que se utilizan al calcular el perímetro y el área de triángulos, cuadriláteros y polígonos regulares. 1 Herramienta Hoja de Cálculo Actividad Fracciones equivalentes (116‐117) Pág. 18 Calculadora Multiplicación y estimación (34) 20 Geometría Dinámica Geometría Dinámica Construcción del paralelogramo (50‐51) Medición de perímetros, áreas y ángulos (60‐61) 21 23 Programación Primer Grado EMAT-HIDALGO Sem. 1ra 2da BLOQUE DOS 4. Justifiquen el significado de fórmulas geométricas que se utilizan al calcular el perímetro y el área de triángulos, cuadriláteros y polígonos regulares. 5. Resuelvan problemas de proporcionalidad directa del tipo valor faltante, con factor de proporcionalidad entero o fraccionario y problemas de reparto proporcional. Sem. 1ra 2da 1. Resuelvan problemas que implican efectuar divisiones con números decimales. 2. Resuelvan problemas que impliquen el uso de ecuaciones de las formas: x + a = b; ax + b = c, donde a, b y c son números naturales y/o decimales. Resuelvan problemas que implican el cálculo de porcentajes o de cualquier término de la relación: Porcentaje = cantidad base x tasa. 3. 4ta Geometría Dinámica Idea de variación (rectángulos) (66‐67) Hoja de Cálculo Variación proporcional 1 (53‐54) Herramienta Actividad Calculadora Transformaciones en un solo paso (39) Hoja de Cálculo Calculadora Hoja de Cálculo 4. 5. 6. Pág. 25 27 Pág. 29 Ecuaciones 1 (61‐62) 30 ¿Qué fracciones faltan? (50) 32 Descuentos y más descuentos (51‐52) 33 MES DE FEBRERO BLOQUE TRES 2da 3ra Actividad MES DE ENERO BLOQUE TRES Sem. 1ra Herramienta 3ra 4ta MES DE DICIEMBRE Resuelvan problemas que implican el cálculo de cualquiera de los términos de las fórmulas para calcular el área de triángulos, romboides y trapecios. Asimismo, que expliquen la relación que existe entre el perímetro y el área de las figuras. Herramienta Actividad LOGO Unidad 4. Polígonos regulares Geometría Dinámica Interpreten y construyan gráficas de barras y circulares de frecuencias absolutas y relativas. Comparen la probabilidad de ocurrencia de dos o más eventos aleatorios para tomar decisiones. Hoja de Cálculo LOGO 2 (43‐46) Cálculo de Áreas (Actividad didáctica) Pág. 35 39 Análisis de textos (142‐143) 43 Unidad 16. Azar y probabilidad (138‐139). 45 Programación Primer Grado EMAT-HIDALGO Sem. 1ra 2da 3ra MESES DE MARZO Y ABRIL BLOQUE CUATRO Herramienta Actividad Identifiquen, interpreten y expresen, algebraicamente o mediante tablas y gráficas, relaciones de proporcionalidad directa. Hoja de Cálculo Variación lineal 1 2. Resuelvan problemas que impliquen el cálculo de la raíz cuadrada y potencias de números naturales y decimales. Calculadora 3. Construyan círculos que cumplan con ciertas condiciones establecidas. Geometría Dinámica 1. 4ta 5ta Justifiquen y usen las fórmulas para calcular el perímetro o el área del círculo. 6ta 1. BLOQUE CINCO Herramienta Resuelvan problemas aditivos que implican el uso de números con signo. Calculadora Calculadora 2. 4ta Sem. 1ra 4ta 4. 49 Punto equidistante (Actividad didáctica) 51 Circunferencia y círculo (Actividad didáctica) Relación entre la longitud de una circunferencia y el área del círculo (68‐70) Unidad 18. Círculos (156‐160). 52 53 56 Hoja de Cálculo Hoja de Cálculo Actividad ¿Cómo sumamos números con signo? (53‐ 54) Sumas y restas de números con signo (55‐57) Adivina qué está pasando (147‐148) ¿Por dónde saldrá? (149‐151) Pág. 61 63 66 68 MES DE JUNIO BLOQUE CINCO 2da 3ra Expliquen las razones por las cuales dos situaciones de azar son equiprobables o no equiprobables. 3. ¡Se descompuso la tecla de la raíz cuadrada! (42‐ 43) MES DE MAYO 2da 3ra Geometría Dinámica LOGO Sem. 1ra (77‐78) LOGO 4. Pág. 47 Herramienta Resuelvan problemas que implican una relación inversamente proporcional entre dos conjuntos de cantidades. Hoja de Cálculo Hoja de Cálculo Hoja de Cálculo Resuelvan problemas que impliquen interpretar las medidas de tendencia central. Hoja de Cálculo 3 Actividad Variación Reciproca I (Actividad didáctica) Variación Reciproca II (Actividad didáctica) Media, Mediana y Moda (Actividad didáctica) Pág. 71 Jugando con las Calificaciones (Actividad didáctica) 74 72 73 U nn ppaasseeoo ccoorrttoo ppoorr uunnaa hhoojjaa ddee ccáállccuulloo El objetivo de esta actividad es que te familiarices con la hoja electrónica de cálculo. En las celdas de una hoja de cálculo puedes introducir: Texto: Escribe la palabra Nombre en la celda A1 (para confirmar oprime la tecla RETURN). Escribe tu nombre en la celda B1. Escribe la palabra Fecha en la celda F1. Escribe la fecha de hoy en la celda G1. Números: Escribe un 8 en la celda C9. Escribe un 9 en la celda D11. Escribe un 7 en la celda E10. Expresiones aritméticas (para que la hoja calcule expresiones aritméticas, debes escribirlas empezando con el signo igual): Escribe = 7 * 2 – 8 en la celda E9 y observa el resultado. Coloca nuevamente el cursor en esta celda y fíjate en la expresión que escribiste en la barra CONTENIDO de la hoja de cálculo. Escribe = 9 – 2 * 2 en la celda D10 y verifica el resultado. Escribe = (9 – 2) * 2 – 10 en la celda C11 y observa el resultado. Fórmulas algebraicas (para escribir fórmulas también debes comenzar con el signo igual): Escribe = C9 – 5 en la celda C10. Explica el resultado: ________________________ ___________________________________________________________________ Escribe = D10 – 4 en la celda D9. Explica el resultado: ________________________ ___________________________________________________________________ Escribe = C11 / 2 en la celda E11. Explica el resultado: _______________________ ___________________________________________________________________ Por último, escribe Cuadrado mágico en la celda D7. Coloca el texto en el centro de la celda presionando el icono CENTRAR. Para revisar si tu cuadrado mágico es correcto, suma cualquier columna o fila. El resultado de la suma siempre deber ser 15. También debes obtener 15 como resultado si sumas cualquiera de las dos diagonales. 4 Lectura y escritura de números Escribe en la calculadora cada una de las cantidades que están descritas con palabras. Cuando vayas marcando los números, ve haciendo con la calculadora las sumas que se indican. Si leíste y escribiste correctamente cada cantidad, obtendrás el total que se indica. Si el total es diferente, busca y corrige el error que cometiste. Cuando hayas producido los números correctos, escríbelos en la columna de la derecha. CANTIDADES EN PALABRAS CANTIDADES CON NÚMEROS Siete millones setecientos ochenta mil cuatro, más ciento veinticinco mil cinco + más doce mil uno, + más trescientos cuarenta y cinco mil ochenta y siete. + TOTAL: TOTAL: 8 262 097 Trece mil noventa y nueve más veinticinco millones ciento cinco + más ciento veintiocho millones ochenta y seis, + más trescientos cinco mil uno. + TOTAL: TOTAL: 153 318 291 Cuatrocientos treinta y seis mil cien, más un millón dos mil, + más quinientos mil veinte, + más trescientos mil treinta. + TOTAL: TOTAL: 2 238 150 Diez millones uno, más dos millones cien, + más treinta y siete mil uno, + más quinientos cuarenta mil diez. + TOTAL: TOTAL: 12 577 112 5 Virus y antivirus Escribe en la calculadora el número 896731425. Supongamos que los nueve dígitos que forman ese número son “virus sumamente peligrosos”. El antivirus consiste en “eliminar” cada dígito, convirtiéndolo en cero mediante una sola operación. Por ejemplo, eliminar el “1” quiere decir que hagas una operación con el número 896731425 y otro número que tú propongas de manera que el resultado sea 896730425. Después de que elimines al 1, debes seguir con el 2, luego el 3, y así sucesivamente. 1. Completa la siguiente tabla para mostrar cómo eliminaste cada “virus”. DÍGITO OPERACIÓN QUE HICISTE EN LA CALCULADORA RESULTADO 1 896730425 2 896730405 3 896700405 4 896700005 5 896700000 6 890700000 7 890000000 8 90000000 9 0 2. Ahora elimina uno a uno todos los dígitos del número 4983.26715. Completa la siguiente tabla para mostrar cómo eliminaste a cada “invasor”. DÍGITO OPERACIÓN QUE HICISTE EN LA CALCULADORA RESULTADO 1 4983.26705 2 4983.06705 3 4980.06705 4 980.06705 5 980.0670 6 980.0070 7 980 8 900 9 0 6 F rraacccciioonneess eeqquuiivvaalleenntteess Cuando repartimos dos barras de chocolate entre cuatro personas, cada una recibe media barra. Así, decimos que: Si repartimos cuatro barras de chocolate entre ocho personas, ¿qué fracción de la barra recibe cada quien? Estos resultados nos indican que las fracciones son equivalentes, ya que el resultado de repartir dos barras de chocolate entre cuatro personas es el mismo que si se repartieran cuatro barras de chocolate entre ocho personas; es decir, en ambas situaciones cada quien recibiría 1 2 Al repartir un pastel entre tres personas, ¿qué fracción recibe cada una? _______________ _______________________________________________ Si se reparten dos pasteles entre seis personas, ¿qué fracción recibe cada una?_________ _______________________________________________ Escribe ambos resultados en fracciones equivalentes: equivalente a:______________________________________________________________ Da otra fracción equivalente a las dos anteriores: ¿Cómo la encontraste?______________________________________________________ _________________________________________________________________________ Un método para encontrar fracciones equivalentes consiste en multiplicar el numerador y el denominador de la fracción por un número en común. Escribe cuatro fracciones equivalentes a la siguiente fracción: Ahora trabajarás con una hoja de cálculo Fracequi.xls. Como puedes observar, en esta hoja a la izquierda aparecen (en amarillo) las fracciones , con sus respectivas fracciones equivalentes a la derecha (en verde). 7 Busca en tu hoja las tres fracciones equivalentes que se te piden a continuación: Los números en amarillo de la hoja se pueden cambiar. Por ejemplo, cambia el de la hoja por y escribe abajo las primeras cuatro fracciones equivalentes dadas en la hoja: Discute con tus compañeros y tu maestro qué significan los números en las celdas grises de la fila 3 (los que están arriba de cada fracción equivalente) y escribe las conclusiones a las que lleguen.___________________________________________________________ ________________________________________________________________________ _________________________________________________________________________ Las fracciones equivalentes son muy importantes para sumar fracciones, ya que sólo se pueden unir fracciones del mismo tipo, es decir, con el mismo denominador (medios con medios, tercios con tercios, etcétera). Por ejemplo, si queremos sumar las fracciones tenemos que encontrar fracciones equivalentes a éstas, pero con el mismo denominador. Busca en tu hoja estas fracciones y escríbelas abajo: Suma con el mismo procedimiento los siguientes grupos de fracciones: 8 C omparar fracciones A veces tenemos que comparar dos fracciones para saber cuál es mayor y cuál es menor. Hay dos maneras fáciles de comparar fracciones: usar decimales, o los productos cruzados. El método decimal de comparar fracciones Sólo tienes que convertir cada fracción en decimal, y comparar los decimales. ¿Cuál es mayor: 3 8 5 o 12 ? Tienes que convertir cada fracción en decimal. Esto lo puedes hacer con Excel. De cualquier manera, la respuesta es: Comparando fracciones 3 5 < 8 12 Realizando el cociente 0.375000 < 0.416667 Así que 5 12 es mayor. El método de productos cruzados Si dos fracciones tienen el mismo denominador (el número de abajo) entonces son fáciles de comparar. Por ejemplo 4 9 es más pequeña que 5 9 (porque 4 es menor que 5) Pero si los denominadores no son iguales necesitas realizar los productos cruzados. 9 Ejemplo: ¿Cuál es más grande: 3 8 5 o 12 ? Si multiplicas 3 × 12 tienes 36, y si multiplicas 8 × 5 tienes 40, así vemos fácilmente que 36 es menor que 40, por tanto 5 12 es mayor. Comparando fracciones 3 5 < 8 12 Productos cruzados 3 por 12 8 < 36 por 5 40 Haciendo uso de la Hoja de Cálculo Compafracc.xls, asigna el símbolo “>”, “=” o “<”, dentro del recuadro a los siguientes ejercicios: 2 3 3 4 4 5 5 9 15 21 5 7 7 10 42 60 23 25 50 70 49 70 16 20 10 G eenneerraannddoo sseeccuueenncciiaass ddee nnúúmmeerrooss Escribe un 4 en la celda A1 y en la celda A2 la fórmula: = A1 + 1. Tu hoja debe verse como sigue: En la celda A3 debes tener el valor 6 y la fórmula: = A2 + 1. En la celda A4 debes tener el valor 7 y la fórmula: = A3 + 1. Si esto es así, ¿qué fórmula debes tener en la celda A5? Compara tu fórmula con la de tu hoja. Cambia ahora el 4 de la celda A1 por el número 15 y observa lo que pasa. ¿Qué secuencia obtienes ahora en la columna A?_______________________________________________ ¿Qué harías para obtener la secuencia 100, 101, 102, 103… en la columna A? ____________________________________________________________________________________ ______________________________________________________________________________Hazlo. Escribe el número 100 en la celda B1. En la celda B2 escribe una fórmula que te dé como resultado el número 99. Cópiala hacia abajo para que obtengas en la columna B la secuencia 100, 99, 98, 97… Tu hoja debe verse como sigue: 11 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .Generando secuencias de números Construye en la columna C la secuencia 1, 3, 5, 7… Recuerda que en C1 debes poner el primer número, en C2 la fórmula que te dé el segundo número y después copiarla hacia abajo. Después construye las siguientes secuencias: En la columna D: 10, 5, 0, -5… En la columna F: 40, 20, 10, 5, 2.5… En la columna E: 1, 2, 4, 8, 16… En la columna G: 5, -5, 5, -5, 5… Discute con el resto del grupo si una fórmula cambia o no cuando se copia hacia abajo. 12 P rrooppiieeddaaddeess ddee llaa ssiim meettrrííaa AAxxiiaall… …… …… …… …… …… …… …… …..Simetría axial Propósito: Utilizar la simetría axial y descubrir algunas de sus propiedades. A continuación veremos un movimiento llamado simetría axial (o reflexión sobre una recta). Para ello, arrastra hacia arriba uno de los vértices del triángulo que está a la izquierda y describe lo que sucede. ______________________________________________________ ______________________________________________________ ______________________________________________________ ______________________________________________________ ______________________________________________________ 13 En este caso, además de la figura inicial, se debe conocer, previamente la recta que se utilizará para obtener la simetría axial. Por lo tanto, dibuja una figura y traza una recta; usa el comando SIMETRÍA AXIAL. Señala primero la figura dada y después la recta elegida; posteriormente aparecerá la figura simétrica respecto de la recta dada. En la simetría axial, ¿cómo son entre sí la figura originalmente dada y la obtenida? _____________________________________________________________________ ¿Qué es lo único que cambia con relación a la figura original? _____________________ _______________________________________________________________________ M 14 T ransformaciones con Simetría axial Haciendo uso de Cabri, realiza las siguientes transformaciones geométricas Con las herramientas: polígono y simetría axial, reproducir: Tenemos dos tipos de congruencia: directa e inversa Directa cuando las puedes sobreponer e inversa cuando tienes que realizar una simetría axial. De izquierda a derecha: ¿Cuáles son directamente congruentes? _______________________ ¿Cuáles son inversamente congruentes? _______________________ Con las herramientas: mostrar ejes, polígono y simetría axial, reproducir: Siguiendo el orden de los cuadrantes: ¿Cuáles son directamente congruentes? _______________________ ¿Cuáles son inversamente congruentes? _______________________ Nota: recuerda que en cabri, puedes manipular las figuras y sus vértices. 15 C oommppaarraannddoo sseeccuueenncciiaass………………………………………………………………………………………….... Piensa en el siguiente problema: Tu papá te ofrece dos opciones para tu gasto semanal. En la primera, te dará 100 pesos para empezar y cada semana incrementará 100 pesos a la cantidad inicial. En la segunda opción, te dará un centavo para empezar, aunque promete que cada semana te dará el doble de la semana anterior. ¿Cuál de las dos opciones escogerías? Para averiguar cuál es la mejor elección, construye la siguiente hoja de cálculo usando fórmulas en la fila 3 para generar las tres series. Extiende tu tabla hasta la semana 52 (un año) y contesta las siguientes preguntas: ¿En qué semana la cantidad de la segunda opción será igual a la de la primera? ________ ___________________________________________________________________________ ¿Cuánto tendría que darte tu papá en la semana 26 (después de medio año) si hubieras escogido la segunda opción?__________________________________________________ ¿Cuánto tendría que darte en esta misma opción en la semana 30?___________________ _________________________________________________________________________ ¿Crees que pueda seguirte pagando tu semana?__________________________________ _________________________________________________________________________ En una secuencia aritmética se suma un número fijo al valor anterior para obtener el siguiente. En una secuencia geométrica se multiplica el valor anterior por un número fijo para obtener el siguiente. ¿Cuál de las secuencias de arriba es geométrica y cuál es aritmética?_________________ _________________________________________________________________________ 16 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Comparando secuencias Clasifica las secuencias de la actividad “Generando secuencias de números” (pp. 11-12) como aritméticas o geométricas. Aritméticas: _______________________________________________________________ Geométricas: _____________________________________________________________ En las líneas de abajo, inventa tres secuencias aritméticas y tres secuencias geométricas: ¾ __________________________________________________________________________ __________________________________________________________________ _______ _________________________________________________________________________ _________________________________________________________________________ ¾ __________________________________________________________________________ _________________________________________________________________________ _________________________________________________________________________ ________________________________________________________________________ ¾ __________________________________________________________________________ _________________________________________________________________________ ________________________________________________________________________ _________________________________________________________________________ 17 F rraacccciioonneess eeqquuiivvaalleenntteess… …… …… …… …… …… …… …… …… …… …… …… ….... Aritmética Ahora trabajarás nuevamente con la hoja de cálculo Fracequi.xls. Observa la siguiente suma y resuelve las preguntas que aparecen en la siguiente página. ¿El 8 puede ser denominador común en esta suma?____________________________ ¿Puede ser denominador común el 16? ______________________________________ ¿Puede haber más? _____________________________________________________ ¿Cuáles? ______________________________________________________________ ¿Cuál sería el mejor? ____________________________________________________ ¿Por qué? _____________________________________________________________ _____________________________________________________________________ Pídele a tu profesor más sumas de fracciones para resolverlas usando esta hoja. Anótalas a continuación: __________________________________________________ __________________________________________________________________________ __________________________________________________________________________ __________________________________________________________________________ 18 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Aritmética Discute en clase el significado de las expresiones Mínimo Común Denominador y Mínimo Común Múltiplo. Pasa a la Hoja2 de la hoja de cálculo Fracequi.xls. Las fracciones que aparecen en amarillo se encuentran simplificadas a la derecha. Por ejemplo, la fracción se puede reducir a (dividiendo entre dos al numerador y al denominador), o a (dividiendo entre tres al numerador y al denominador). Si colocas en la segunda fila amarilla, la fracción se simplificará a o a. Si colocas en la tercera fila amarilla, verás que esta fracción no puede simplificarse dividiéndola entre dos, pero sí entre tres. Como has visto, esta hoja te puede ayudar a simplificar fracciones. Por ejemplo, se puede simplificar dividiendo entre dos al numerador y al denominador, luego otra vez entre dos, y finalmente entre tres para llegar a . Simplifica de la misma manera Simplifica ahora y describe cómo procediste.______________________ y describe cómo procediste. _____________________________ _____________________________________________________________________ 19 Multiplicación y estimación 1. En cada inciso escribe dos números tales que al multiplicarlos den el resultado que se indica. Los números que utilices en cada inciso deben ser distintos de uno. 0.001 0.206 0.765 a) d) g) b) e) h) c) f) i) 0.784 3.519 19.873 j) m) o) k) n) p) l) Ñ) q) 2 ¿Qué hiciste para obtener los números que se piden en el inciso 1? Describe el procedimiento de manera que cualquiera de tus compañeros lo entienda. Si quieres hazlo con un ejemplo __ _________________________________________________________________________ _________________________________________________________________________ _________________________________________________________________________ _________________________________________________________________________ 3 En cada inciso escribe dos números tales que, al multiplicarlos, den por resultado un número que esté entre los números que se dan en cada inciso. 0.1003 y 0.1007 5.10207 y 5.10209 7.30 y 7.31 a) d) g) b) e) h) c) f) i) 20 C oonnssttrruucccciióónn ddee ppaarraalleellooggrraammoo…………………….. Figuras básicas y ángulos Propósito: Que el alumno construya una definición equivalente de paralelogramo. En el dibujo aparece un paralelogramo; esto es, una figura formada por dos pares de rectas paralelas que se intersectan. Traza las diagonales del paralelogramo. ¿Cuál es la longitud de cada una de las diagonales?_____________________ Las diagonales se intersectan en un punto, que es el punto medio de cada una de ellas; verifícalo. 21 … …… …… …… …… …… …… …… …… …… …… …… …… …… …… …… …… …… …… …....… …… …PPrriim meerr ggrraaddoo Arrastra un vértice del paralelogramo con el puntero y describe lo que sucede: ______________________________________________________ ______________________________________________________ ______________________________________________________ ______________________________________________________ ______________________________________________________ El punto de intersección de las diagonales es el centro del paralelogramo. Ahora, si tienes dos segmentos y haces que el punto medio de ambos coincida a modo de que formen un ángulo cualquiera, ¿podrías construir un paralelogramo? Si tu respuesta fue afirmativa, construye la figura. En la construcción que realizaste, arrastra una de las diagonales y verifica que los lados opuestos son siempre paralelos. 22 M eeddiicciióónn ddee ppeerríím meettrrooss,, áárreeaass… …… …… …… …....… …Calculo de perímetros yy áánngguullooss Propósito: Usar las herramientas para medir longitudes, áreas y ángulos. Escribe lo que entiendes por cuadrilátero y haz un dibujo para ilustrarlo. _______________________________________________________ _______________________________________________________ _______________________________________________________ _______________________________________________________ La siguiente figura es un cuadrilátero con las medidas de sus ángulos y de sus lados. 23 y áreas Reproduce otro cuadrilátero en el ambiente de Geometría Dinámica. Anota los pasos que seguiste para realizar el ejercicio anterior. ¿Cuánto suman los ángulos interiores de un cuadrilátero? _________________________________________________ _________________________________________________ _________________________________________________ _________________________________________________ _________________________________________________ _________________________________________________ ¿Qué entiendes por perímetro? ¿Cómo perímetro? calculas el _________________________________________________ _________________________________________________ _________________________________________________ _________________________________________________ 24 I ddeeaa ddee vvaarriiaacciióónn ((rreeccttáánngguullooss))… …… …… …… …… …Calculo de perímetros y áreas Propósito: Conocer la idea de variación. m A n C B n m área del rectángulo =6.70 cm2 En el dibujo se tiene el segmento de extremos A y B, sobre el cual se eligió un punto cualquiera C, que determina los segmentos AC de longitud m y CB de longitud n; con estos dos segmentos de longitudes m y n, respectivamente, se construyó un rectángulo (con trazos punteados se indican los trazos realizados con los comandos: COMPÁS, PERPENDICULAR, MARCA DE ÁNGULO y PARALELA); enseguida, se colorearon los segmentos mencionados, el rectángulo, y se calculó su área. Con el puntero arrastra C y describe lo que le sucede al área del rectángulo, en particular, cuando C se acerca a cualquiera de los extremos A y B. _______________________________________________________ _______________________________________________________ _______________________________________________________ _______________________________________________________ 25 … …… …… …… …… …… …… …… …… …… …… …… …… …… …… …… …… …… …… …....… …… …PPrriim meerr ggrraaddoo m 3.52 cm n 1.90 cm. m+n 5.42 cm Mn 6.70 cm2 En este nuevo dibujo, que es el anterior sin los trazos punteados, aparece en la parte superior izquierda una tabla, cuyos encabezados son m, n, m+n y mn, en la que aparecen la longitud del segmento AC, después la longitud del segmento CB, luego el resultado de la suma de los dos segmentos anteriores, esto es, el semiperímetro del rectángulo o la longitud del segmento dado AB y finalmente el área del rectángulo. Arrastra el punto C, del segmento dado AB y describe lo que le ocurre a los números que aparecen en la tabla. ¿Qué ocurre cuando el punto C coincide con uno de los extremos del segmento AB? Descríbelo a continuación. _______________________________________________________ _______________________________________________________ _______________________________________________________ _______________________________________________________ _______________________________________________________ _______________________________________________________ _______________________________________________________ _______________________________________________________ Habrás observado que el semiperímetro del rectángulo, esto es m+n, no cambia, sin embargo, el área del rectángulo varía, desde el valor cero hasta un valor máximo. ¿Para qué posición del punto C, al variar sobre el segmento AB, se encuentra este valor máximo del área del rectángulo? _____________ ¿Cómo son m y n cuando el área es máxima? ______________________________________________ ¿Cuál de todos los rectángulos que tienen el mismo semiperímetro es el que tiene mayor área? ____________________________________________________________________________________ 26 V aarriiaacciióónn pprrooppoorrcciioonnaall ((11))… …… …… …… …… …..… …… …… …… …… …… …… … Aritmética La cantidad de dólares y su equivalente en pesos, así como la distancia recorrida por un coche y el tiempo que tarda en recorrerla son cantidades relacionadas. A continuación se abordará este tema. Pensemos primero en la situación en la que un dólar se puede cambiar por 8 pesos. ¿A cuántos pesos equivaldrían 2 dólares?_______________________________________ ¿A cuántos pesos equivaldrían 4 dólares? ______________________________________________ ¿A cuántos pesos equivaldrían 5 dólares?_______________________________________ Construye una hoja de cálculo relacionando estas dos cantidades. La fórmula de A3 es = A2 + 1. La fórmula de B2 es = 8 * A2. Escribe ahora la fórmula de la celda B3. ________________________________________ Escribe la fórmula de la celda B6.______________________________________________ En general podemos escribir: columna B = factor * columna A ¿Cuál es el factor en el ejemplo anterior? _______________________________________ Piensa ahora en un coche que va a una velocidad constante de 80 km/h. Las dos cantidades que consideraremos son la distancia recorrida (d) y el tiempo que tarda en recorrerla (t). 27 ¿Qué distancia recorrió en 2 horas? ___________________________________________ ¿Qué distancia recorrió en 4 horas? ___________________________________________ ¿Qué distancia recorrió en 5 horas y media? ____________________________________ Construye una hoja de cálculo relacionando ambas cantidades. La fórmula de la celda A3 es = A2 + 1. La fórmula de la celda B2 es = A2 * v. Escribe la fórmula de la celda B3:_____________________________________________ Escribe la fórmula de la celda B6:_____________________________________________ ¿Cuál es el factor en el ejemplo anterior? ______________________________________ Cuando una cantidad se obtiene multiplicando otra por un factor constante se obtiene una variación proporcional. A continuación se plantean algunas preguntas para conocer otra propiedad de este tipo de variaciones. ¿Qué le pasa a la distancia recorrida si duplicamos el tiempo? _______________________ ________________________________________________________________________ Por ejemplo: ¿Cuántos kilómetros recorre el coche en cinco horas? _____________________________ Si se duplica el tiempo, ¿ocurre lo mismo con la distancia? __________________________ 28 Transformaciones en un solo paso En cada uno de los siguientes casos encuentra al menos dos formas para obtener, a partir del número de arriba, los números que se indican abajo. 1. 19 19 × 0.01 1900 0.19 0.0019 19.19 0.0235 2.350 30000 0.0303 2. 2.35 2350 235 3. 0.3 3 0.0003 4. Una alumna dice que 1.5 es igual a 1.5000. ¿Tiene razón? ___________________ ¿Por qué? ____________________________________________________________________________ _____________________________________________________________________________________ 29 E ccuuaacciioonneess ((11))………………………………………………………………..…………………………………… Pre álgebra Dentro de las matemáticas, una habilidad importante consiste en poder expresar relaciones verbales entre cantidades por medio de fórmulas. Por ejemplo, ¿cómo escribirías con símbolos: “un número es la octava parte de otro número”? Una hoja de cálculo como la que se sugiere a continuación puede ayudarte a comprobar que la expresión matemática que propusiste es correcta. Escribe tu expresión matemática en la celda B2. ¿Obtuviste el resultado que esperabas? (Si no fue así, consulta a tus compañeros para saber cómo procedieron). Cambia el número 8 en la celda A2 por el 16 y por el 4 para comprobar que tu expresión es correcta. Construye una hoja de cálculo similar a la anterior, pero ahora el encabezado de la primera columna será ”Cantidad de artículos vendidos“ y el de la segunda columna será “Costo total”. Considera que cada uno se vende a $85. Para comprobar tu fórmula cambia el número de artículos, por ejemplo 1, 10 y 100. ¿Cuál sería la fórmula algebraica apropiada? ____________________________________ ________________________________________________________________________ Incluye dos columnas más en tu hoja de cálculo (observa el ejemplo de abajo). Registra en una la cantidad vendida de un segundo artículo y en la otra el costo de los artículos. Considera que el precio de cada uno es de $150. Usa la quinta columna para calcular el costo total de los dos artículos. Varía el número de ambos artículos, por ejemplo con 0, 1, 10 y 100 para comprobar tus fórmulas. 30 ¿Cuál sería la fórmula algebraica del costo del primer artículo? (Usa n para expresar la cantidad del primer artículo.) ________________________________________________________________________ ¿Cuál sería la fórmula algebraica del costo del segundo artículo? (Usa m para expresar la cantidad del segundo artículo.) ________________________________________________________________________ ¿Cuál sería la fórmula algebraica del costo de ambos artículos? ______________________ ________________________________________________________________________ Veamos ahora un ejemplo diferente. Escribe una ecuación que exprese lo siguiente: “Dos personas se reparten $750” Considera a A como la cantidad que le toca a una de las personas y como B a la cantidad que le toca a la segunda. Elabora una hoja de cálculo como la siguiente y escribe en la celda B2 una expresión que haga que el total de las dos cantidades en las columnas A y B sea 750. Comprueba tu fórmula variando la cantidad de la primera persona. Para terminar resuelve la siguiente cuestión: Un número es 15% mayor que otro. Construye una hoja de cálculo que te ayude a escribir esta relación en forma algebraica. 31 ¿ Qué fracciones faltan? 1. Usa la calculadora para encontrar las fracciones que faltan. a) 2 + a = 1 5 La fracción que falta es: c) 1 1 + + f = 1 7 4 b) La fracción que falta es: d) f = 2 3 e) 1 + 2 1 1 + + c =1 3 5 2 1 1 + + + h = 2 3 4 5 h = 1 1 + 3 + p = 10 4 6 f) p = 2 3 1 1 1 + 2 + m + 3 = 11 5 4 6 2 m = 2. ¿Qué hiciste para contestar las preguntas anteriores? ________________________________ _ __________________________________________________________________________________ __________________________________________________________________________________ 3. Usa la calculadora para encontrar las fracciones que faltan a) 2 1 −x= 3 5 La fracción que falta es: c) 3− m = 3 7 La fracción que falta es: e) 27 −q = 6 4 La fracción que falta es: b) 3 3 −y= 4 8 La fracción que falta es: d) 5 1 −a = 8 5 La fracción que falta es: f) 1 1 −b = 3 4 La fracción que falta es: 4. ¿Encontraste un método para contestar las preguntas anteriores? ¿Cuál?_______________ ________________________________________________________________________ 32 D eessccuueennttooss yy mmááss ddeessccuueennttooss…………………………..………………………… Aritmética Si se aplica un descuento extra de 30% después de haber aplicado uno de 20%, ¿qué descuento total se obtiene? __________________________________________________ En esta actividad estudiarás situaciones de este tipo y posiblemente te sorprenderás con los resultados. Empecemos con la situación de un solo descuento En las celdas C2 y D2 de la hoja de cálculo escribe las fórmulas para determinar la cantidad descontada y el precio con descuento, de acuerdo con los datos de las celdas A2 y B2 (recuerda que para hacer cálculos, 20% se escribe 0.2). Prueba tu hoja poniendo cantidades con las que puedas calcular el resultado mentalmente. Si el precio original de un coche es de $82 000.00 y los vendedores ofrecen 13% de descuento, ¿cuál es el precio final? Un traje con 30% de descuento vale $875.00. ¿Cuál era el precio original? Hay dos maneras de averiguarlo: la primera consiste en tratar de adivinar el precio normal hasta llegar al precio con descuento. La segunda es construir otra hoja de cálculo que realice esta conversión: Precio con descuento Precio normal Usa por lo pronto el primer método. El segundo queda como tarea. Pasemos ahora a agregar un descuento adicional. Para ello observa la siguiente hoja de cálculo. Tienes que trasladar el precio con descuento a la celda B5 con una fórmula. Introduce las fórmulas apropiadas en las celdas C5 y D5. 33 ……………………………………………………………………………….………Descuentos y mas descuentos Cambia ahora el precio normal a $100.00. En la columna “Precio con descuento” el resultado debe ser $80.00 y en “Precio con descuento extra” debe ser $56.00. ¿Cuál fue entonces el descuento total? _________________________________________ ¿Cuál será el descuento total si se aplica primero un descuento de 50% y al precio con descuento se le aplica otro 50%? ______________________________________________ Un padre de familia tiene que pagar $1500 de colegiatura. La escuela le otorga 25% de descuento y después su hijo recibe una beca que representa 20% de la colegiatura. La escuela afirma que debe pagar $900, pero él dice que sólo debe pagar $825. Explica cómo llegaron cada uno a estas cantidades y discute quién tiene la razón. ¿Infiere en algo si primero se aplica el descuento que corresponde al porcentaje de la beca y después el descuento que otorga la escuela? ___________________________________ ________________________________________________________________________ 34 Polígonos regulares • Escribe el procedimiento para que la tortuga dibuje un cuadrado. • ¿Y un triángulo equilátero? • Escribe procedimientos para dibujar tantos polígonos regulares como puedas y llena la tabla de la siguiente página. 35 Polígono Número de lados Ángulo de rotación Triángulo 120° Cuadrado 4 Pentágono Hexágono 6 Octágono 45° ……….. N • Encuentra la relación entre el número de repeticiones y el ángulo. REPITE [ AV 20 GD ] ¿CONEXIONES? • Escribe tus observaciones. _____________________________________________________________________________________ _____________________________________________________________________________________ _____________________________________________________________________________________ _____________________________________________________________________________________ 36 Generaliza: Un procedimiento para cualquier polígono regular • ¿Cómo escribirías un procedimiento para dibujar cualquier polígono regular? 37 De polígonos a circunferencias. Usando tu experiencia en dibujar polígonos regulares: • ¿Puedes escribir un procedimiento para dibujar un círculo? • ¿Puedes hacer círculos de diferentes tamaños? 38 Cálculo de áreas Justificación de fórmulas Área de un paralelogramo. Si partimos el paralelogramo ABCD por la línea punteada determinamos un triángulo BEC, que si lo trasladamos, podemos formar un rectángulo BEFA, como se muestra en la ilustración. ¿Cómo son las bases del paralelogramo y del rectángulo? _________________ ¿Y sus alturas? _____________________ Calcula el área del paralelogramo y el rectángulo, ¿cómo son entre sí? ____________ Recuerda que para calcular el área de un rectángulo se multiplica la base por la altura. ¿Qué harías para calcular el área del paralelogramo? Explica: __________________ __________________________________________________ Escribe la fórmula para calcular su área: ____________ ¿Cómo se obtiene la fórmula para calcular el área de un paralelogramo en un caso como el siguiente? 39 Área del triángulo Construye con el software un rectángulo como se muestra enseguida y calcula su área. Para verificar que la construcción fue realizada adecuadamente, arrastra uno de los vértices ¿Sigue siendo rectángulo? _______ Traza el segmento BD, y determina el triángulo BCD. ¿Cuál es su área? ¿Qué relación existe entre el área del rectángulo y el área del triángulo? Realiza la misma actividad con las siguientes figuras: Área del paralelogramo ABCD = Área del triángulo ABC = 40 II) En la siguiente construcción el punto E está determinado como punto sobre objeto en el segmento BC. Calcula el área del rectángulo ABCD = Calcula el área del triángulo AED = Al desplazar el punto E ¿cambian las áreas del triángulo AED? __________ Con los triángulos ABE y DEC ¿puedes construir un triángulo? ________ ¿Qué área tiene? __________ III) Con ayuda del software realiza lo que se indica: Construye un triángulo ABC (Fig.1), y traza paralelas por cada vértice al lado opuesto. (Fig.2) Fig.1 Fig.2 A partir de la figura 2 obtenida, responde: Los paralelogramos YABC y AZBC, ¿tienen la misma área? ________ Los paralelogramos ZBCA y BXCA, ¿tienen la misma área? _________ Los paralelogramos XCAB y CYAB, ¿tienen la misma área? __________ 41 Cada uno de los seis paralelogramos mencionados contienen al triángulo ABC, el área del triángulo ABC, ¿cómo es respecto al área del cualesquiera de los seis paralelogramos? ____________ El área de un triángulo no depende de qué lado se elija como la base. IV) Reproduce la siguiente figura y contesta. ¿Tienen la misma área las dos partes sombreadas? __________ Explica: __________________________________________________________ Para verificar tu respuesta, usa la herramienta Área para obtener el área de los dos rectángulos sombreados. ¿Qué relación encuentras entre sus áreas? __________ Al mover el punto G sobre la diagonal AC, qué ocurre con las áreas de los rectángulos HGFD y EBIG? ________________ ¿Por qué sucede esto? __________________________________________________ Reproduce la figura de tal manera que conserve las condiciones y relaciones entre las figuras, aún con el arrastre. Área del trapecio. Construye con el software un trapecio como se muestra enseguida y calcula su área. Determina dos triángulos a partir del trapecio ABCD. Calcula el área de los triángulos ABC y ACD. Con la herramienta calcular obtén la suma de las áreas de los triángulos y compara con el área del trapecio. Modifica una de las dimensiones del trapecio. ¿Qué observas? _____________________________________________________________________ ¿Qué harías para calcular el área de un trapecio? _____________________________________________________________________ 42 V aarriiaacciióónn pprrooppoorrcciioonnaall ((33)) … …… …… …… …… …… …… …… …… …… …… …… …… ….. Aritmética Abre el archivo Anatex95.xls. Verás un texto en amarillo que está guardado en la celda B1. Explora esta hoja de cálculo para que deduzcas lo que hace. ¿Qué contiene la parte azul? ____________________________________________ ¿Qué contiene la parte verde? ___________________________________________ Cambia el texto de la celda B1 por uno pequeño que tú quieras. Observa las secciones azul y verde. Verifica que el valor del Largo y que las cantidades de cada símbolo son la correctas. Observa que la parte azul llega hasta 255 letras (ésta es la máxima capacidad de análisis de un texto). Cambia ahora el texto de la celda B1 por otro texto que sea mayor de 200 letras pero que no rebase el límite de 255 (no tienes que contar el número de letras, pues la hoja te lo dice al aceptarlo). ¿Cuál es la letra que aparece con más frecuencia en tu texto?__________________ ¿Cuántas veces? _____________________________________________________ Calcula el porcentaje de esta letra dentro del total de letras de tu texto de la siguiente manera: Calcula el porcentaje de espacios dentro de tu texto de la siguiente manera: En la celda E38 se calcula el número de palabras. Fíjate en la fórmula y explícala. _________________________________________________________________________________ Observa ahora la gráfica. Si tuvieras que adivinar las letras que aparecen en una palabra cualquiera, ¿con cuáles empezarías? _____________________________________________________ En la tabla que aparece en la página siguiente ordena las ocho letras que aparecen con mayor frecuencia y calcula, como lo hiciste anteriormente, el porcentaje de cada letra. 43 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Análisis de textos Compara tu tabla con la de tus compañeros para que observen sus diferencias y similitudes. Escribe en la celda B1 el siguiente texto en inglés. The sun did not shine. It was too wet to play. So we sat in the house all that cold, cold, wet day. I sat there with Sally. We sat there, we two. And I said, How I wish we had something to do. Too wet to go out and too cold to play ball (The cat in the hat, Doctor Seuss). Analízalo y compara tus resultados con los de tu texto en español. 44 Adivina qué hago (la primitiva AZAR) • Prueba o siguiente: • Prueba varias veces con la misma entrada y registra tus resultados en la tabla: 45 • Explica qué hace la primitiva AZAR ___________________________________________________________________________ ___________________________________________________________________________ ___________________________________________________________________________ • ¿Qué pasaría si tecleo AZAR 24? ___________________________________________________________________________ ___________________________________________________________________________ ___________________________________________________________________________ • Usando AZAR, ¿puede escribir un procedimiento que te devuelva el resultado de lanzar un dado. 46 V aarriiaacciióónn lliinneeaall ((11)) … …… …… …… …… …… …… …… …… …… …… …… …..… …… …… …… …… ….. Aritmética ¿Qué tienen en común el costo de un viaje en taxi y el cocinado de un pavo? En matemáticas los fenómenos reales se clasifican de acuerdo con el tipo de modelo matemático que los describe. En esta actividad verás que las dos situaciones mencionadas coinciden en su estructura matemática. Considera primero el viaje en taxi. Imagina que al subir, en el medidor aparece ya la cantidad de $5.00 y que ésta aumenta $1.50 por cada kilómetro que el taxi recorre. ¿Cuánto habrá que pagar en total si el recorrido es de 4 kilómetros? _______________________ _______________________________________________________________________________ Las operaciones que hiciste posiblemente fueron: 1.5 * 4 + 5 = 11 Una fórmula general para hacer estos cálculos es: 1.5 * (km recorridos) + 5 = Cantidad a pagar Utiliza una hoja de cálculo para obtener una tabla que represente esta situación. En la columna A coloca los kilómetros recorridos e increméntalos de uno en uno empleando una fórmula. En la columna B calcula la cantidad a pagar con la fórmula general: A B C 1 KILÓMETROS CANTIDAD CANTIDAD RECORRIDOS A PAGAR A PAGAR (2) 2 0 5 3 1 6.5 4 2 8 ¿Cuánto hay que pagar por un recorrido de 15 kilómetros? _______________________________ _____________________________________________________________________________________ En otra ciudad se cobra sólo $1.00 por el banderazo, pero $2.00 pesos por kilómetro recorrido. Agrega en la columna C la fórmula para esta ciudad. Compara los resultados para averiguar qué ciudad brinda el servicio más barato. 47 Variación lineal (1) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Ocúpate ahora de cocinar el pavo. En un libro de cocina aparece la siguiente sugerencia: Envuelva el pavo en papel aluminio; por cada kilogramo de peso, hornee el pavo 15 minutos y sume a esto 90 minutos extras. ¿Cuánto tiempo de cocinado necesita un pavo de 8 kilos? _______________________________ _______________________________________________________________________________ Las operaciones que posiblemente hiciste fueron: Una fórmula general para hacer estos cálculos es: Usemos otra hoja de cálculo para obtener una tabla que represente esta situación. En la columna 15 * 8 + 90 = 210 15 * (kg de peso) + 90 = minutos de cocinado A anota los kilogramos de peso. En las columnas B y C calcula el tiempo de cocinado con fórmulas. 1 2 A KG. DE PESO 1 B MINUTOS DE COCCIÓN 105 C HORAS DE COCCIÓN 1.75 3 2 120 2 4 3 135 2.25 ¿Cuánto tiempo se requiere para cocinar un pavo de 6.5 kilos? ____________________________ _______________________________________________________________________________ Si observa las dos fórmulas, la del taxi y la del pavo, notarás que son muy similares. Ambas pueden expresarse así: a * x + b = y o bien y = a * x + b donde a y b son números constantes y las variables están representadas por x y y. 48 ¡Se descompuso la tecla de la raíz cuadrada! 1. Supongamos que la tecla que indica esta operación se descompuso. ¿Qué podrías hacer, sin usar la raíz cuadrada, para contestar las siguientes preguntas? a) ¿Cómo puedes encontrar la raíz cuadrada de 25? ___________________________ __________________________________________________________________ b) ¿Cómo puedes encontrar la raíz cuadrada de 81? ___________________________ c) ¿Cuál es el número entero que mejor se aproxima a 53 ?_____________ __________ d) ¿Cuál es el número entero que mejor se aproxima a 75 ? _______________________ e) ¿Puedes encontrar una aproximación para la raíz cuadrada de 133 con número entero y una cifra decimal? ¿Cuál es? _________________________________________________ f) ¿Puedes encontrar una mejor aproximación para la raíz cuadrada de 133 con un número entero y tres cifras decimales? ¿Cuál es? _______________________________________ g) ¿Puedes encontrar una mejor aproximación que las que obtuviste para la raíz cuadrada de 133 con cuatro cifras decimales? ¿Cuál es? ___________________________________ 2. Podemos tener una aproximación a un número “por abajo” o “por arriba”. Por ejemplo, 6.7 es una aproximación “por abajo” para el número 7, y 7.1 es una aproximación “por arriba”. Observa que 7.1 es una mejor aproximación que 6.7, porque 7.1 – 7 = 0.1, mientras que 7 – 6.7 = 0.3, es decir, 7.1 está “más cerca” del 7 que de 6.7 ¿Puedes encontrar una mejor aproximación “por arriba”? ____________________________ ¿Cuál es? ___________________________________________________________________ 3. Sin usar la tecla de la raíz cuadrada encuentra la mejor aproximación “por abajo”, con un número entero y una cifra decimal, para la raíz cuadrada del 72. ¿Cuál es esa aproximación? _________________________ Explica qué es lo que te permite afirmar que la aproximación que encontraste es la mejor “por abajo” con una cifra decimal para la raíz cuadrada de 72. _______________________________________________________________________________ _______________________________________________________________________________ _______________________________________________________________________________ _______________________________________________________________________________ 49 ¿Cómo me aproximo…, por abajo o por arriba? 1. Encuentra la mejor aproximación “por abajo” para cada una de las siguientes raíces cuadradas. Tu aproximación debe tener dos cifras decimales. Recuerda que no debes usar la tecla que indica esta operación. a) 37 = b) 97 = c) 108 = d) 90 = e) 134 = f) 130 = g) 452 = h) 725 = i) 927 = 2. Encuentra la mejor aproximación “por arriba” para cada una de las siguientes raíces cuadradas. Tú aproximación debe tener tres cifras decimales, y no debes usar la tecla de la raíz cuadrada. a) 48 = b) 227 = c) 326 = d) 405 = e) 618 = f) 853 = g) 958 = h) 1104 = i) 1005 = 3. Encuentra la mejor aproximación “por arriba” y la mejor aproximación “por abajo”, con tres cifras decimales, para el número 2 ________________ < 2 < ____________________ 50 CIRCUNFERENCIA Y CÍRCULO Punto equidistante Haciendo uso de Cabri y partiendo de las siguientes definiciones: Pasos a seguir Circunferencia es la línea curva cerrada y plana cuyos puntos están a la misma distancia (radio) de un punto (centro). Círculo es la superficie plana limitada por una circunferencia. a) Dibuja una Semirrecta con origen “O” b) Con punto sobre objeto sobre la semirrecta define “P” c) Después con Traza activada, presiona a “P” d) Finalmente con Animación de la Semirrecta a) Dibuja una circunferencia con centro “O” y radio arbitrario b) Traza una cuerda AB c) Localiza el punto medio “M” de AB d) Después con Traza activada, presiona a “M” e) Finalmente con Animación del punto “A” 51 a) Con segmento une O y P b) Después con Traza activada, presiona al segmento anterior c) Finalmente con Animación de la Semirrecta CIRCUNFERENCIA Y CÍRCULO (parte 2) Utilizando la primitiva “Circle” y el procedimiento “Polireg”, en el ambiente de LOGO Por ejemplo: Circle 100 circle 50 Produce el siguiente dibujo La primitiva Circle __ construye una circunferencia con centro donde se encuentra la tortuga y radio el que uno introduzca. Aplicando tu ingenio reproduce las siguientes construcciones 52 R eellaacciióónn eennttrree llaa lloonnggiittuudd ddee uunnaa… …… …… …… …....… …… … Cálculo de perímetros cciirrccuunnffeerreenncciiaa yy eell áárreeaa ddeell cciirrccuulloo y áreas Propósito: Descubrir la relación entre la longitud de la semicircunferencia y el área del círculo Arriba puedes ver una circunferencia y un círculo divididos en cuatro partes iguales; a la derecha, estas cuatro partes se encuentran alternadas horizontalmente sin encimarse. Usa un color para rellenar dos partes del círculo alternadamente y otro para las dos partes restantes. Usa los mismos colores para rellenar las partes correspondientes en la configuración de la derecha. Si sumas las medidas de los dos arcos del mismo color que aparecen en esta configuración, los de arriba o los de abajo, ¿qué representa esta suma? __________________________________________ _______________________________________________________________________________ Veamos lo que sucede si la circunferencia y el círculo se dividen en ocho partes iguales: 53 … …… …… …… …… …… …… …… …… …… …..… …… …… …… …… …… …… …… …… …… …… …PPrriim meerr ggrraaddoo Ahora, la circunferencia y el círculo están partidos en ocho partes iguales, como se aprecia a la izquierda; en la configuración de la derecha, se tienen estas ocho partes alternadas horizontalmente sin encimarse. Colorea alternadamente cuatro partes del círculo de la izquierda; después ilumina en la configuración de la derecha, las cuatro partes que correspondan a las que coloreaste en el círculo. Si sumas las medidas de los cuatro arcos del mismo color que aparecen en la configuración de la derecha, los de arriba o los de abajo, ¿qué representa esta suma? Si volvemos a dividir cada una de estas ocho partes en dos partes iguales, ¿en cuántas partes iguales quedará dividida toda la circunferencia y el círculo? _____________________________________ Veamos lo que resulta de esta nueva subdivisión: A la izquierda, la circunferencia y el círculo quedaron divididos en 16 partes iguales; a la derecha se encuentra la configuración que resulta de colocar estas 16 partes iguales alternadas horizontalmente sin encimarse. Colorea alternadamente el círculo y usa el mismo color para rellenar las partes correspondientes en la configuración de la derecha, ¿Cuánto suman las medidas de los arcos de un mismo color, en la configuración? _________________________________________________________________________ _____________________________________________________________________________________ _________________________________________________________________________________ 54 Cálculo de perímetros y áreas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Fíjate en las tres configuraciones presentadas. A medida que aumenta el número de partes iguales en que se dividen la circunferencia y el círculo, los arcos de cada una de las partes se asemejan a los segmentos que unen sus extremos; dibuja en el espacio siguiente la configuración que resulta de dividir la circunferencia y el círculo en 32 partes iguales. La configuración que realizaste, ¿es casi un rectángulo? __________________________________ Si tu respuesta fue afirmativa, ¿cuánto mide el largo y cuánto mide el ancho?_______________________ Por lo tanto, cómo es el área del casi rectángulo_____________________________ Y cómo es el casi rectángulo que se construyó con las partes del círculo de la izquierda, entonces ¿cuál es el área de este círculo?_______________________________________________________________________________ 55 Arcos • Anteriormente, con Polígonos regulares, construiste una circunferencia utilizando un procedimiento parecido al siguiente • Basándote en este procedimiento, ¿puedes crear otro que construya • ¿Un cuarto de circunferencia?, ¿un tercio de circunferencia? 56 • Construye un procedimiento general que, usando una variable, construya un arco que sea una fracción cualquiera de la circunferencia. • Dibuja una circunferencia formada a partir de arcos cada uno de diferente tamaño y color. Usa PONCOLORLAPIZ o PONCL. • ¿Cuánto deben sumar todos los arcos? __________________________________ 57 Pétalos y flores Usa ARCO para construir una flor. Una manera (constrúyela) es creando los siguientes componentes. Escribe aquí tus procedimientos. ¿De qué otra manera puedes construir una flor usando ARCO? 58 Diámetros y radios Usando el siguiente procedimiento: ¿Cuál es el perímetro de la circunferencia que se dibuja? ___________________________________________________________________________ ___________________________________________________________________________ Construye un procedimiento que trace el diámetro de esa circunferencia. Úsalo para construir las siguientes figuras. 59 Construye ahora un procedimiento que trace el radio de esa circunferencia. Úsalo para construir la siguiente figura. 60 ¿Cómo sumamos números con signo? En las siguientes hojas de trabajo, aprenderás cosas importantes sobre los números negativos. Los números con signo pueden ser positivos o negativos y el cero no es positivo ni negativo. Los números positivos los conoces bastante bien. Los números negativos se pueden usar en ciertas situaciones, Por ejemplo, la temperatura “siete grados bajo cero” se puede representar mediante la expresión –7 grados. También se usan para referirse a deudas, por ejemplo, si una persona debe $ 1000. 00, puede representarse mediante la expresión –1 000 pesos (se lee “menos mil pesos”) ¿Puedes dar otro ejemplo de una situación en que se usen los números negativos? _____________________________________________________________________________________ _____________________________________________________________________________________ ________________________________________________________________ 1. Utiliza la calculadora para realizar las siguientes actividades. Nota que en la calculadora hay dos signos que representan “menos”. Uno de esos signos sirve para efectuar la operación de restar; el otro (–) es el que debes usar para escribir un número negativo en la calculadora. 1) –7 + 9 = 2) –5 + –7 = 3) 8 + –7 = 4) –15 + –17 = 5) –30 + –50 = 6) 0.5 + –2 = 7) –19 + –30 = 8) –72 + 30 = 2. ¿Qué operaciones hizo la calculadora para sumar un número negativo con un número positivo? __________________________________________________________________ _________________________________________________________________________ 3. ¿Qué operaciones hizo la calculadora para sumar un número negativo con otro negativo? ________________________________________________________________________________ __________________________________________________________________ 4. ¿Qué operaciones hizo la calculadora para poner el signo al resultado? _________________________________________________________________________ _________________________________________________________________________ 61 5. En cada inciso encuentra tres parejas de números que al sumarlos den el resultado que se indica. Verifica tus respuestas mediante la calculadora. a) Resultado: –32 b) Resultado: –45 c) Resultado: –27 d) Resultado: –40 e) Resultado: –55 f) g) Resultado: 0 h) Resultado: –1 Resultado: –78 62 Sumas y números con signo 1. Obtén tres números que al sumarlos den por resultado cero. ___________________________ ____________________________________________________________________________ 2. ¿Puedes encontrar cuatro números que al sumarlos den por resultado –1? ¿Cuáles son?______ ____________________________________________________________________________ 3. Encuentra cinco números que al sumarlos den por resultado –27. _______________________ ____________________________________________________________________________ 4. Construye una suma con tres sumandos de manera que el resultado sea –0.25. ____________ ____________________________________________________________________________ 5. Construye una suma con cuatro sumandos, dos positivos y dos negativos, de manera que el resultado sea –0.763. ____________________________________________________________ 6. Construye una suma con cinco sumandos, dos negativos y tres positivos, de manera que el resultado sea 38.5. _______________________________________________________________________ 7. Construye una suma con cinco sumandos, cuatro negativos y uno positivo, de manera que la suma sea –7.328. ___________________________________________________________________ 8. Encuentra los números que faltan. Verifica tus respuestas con la calculadora, no debes tener ningún error. c) p + 18 + −35 = −100 b) 17 + −20 + n = −75 a) − 15 + 13 + m = 0 m = n = p = d) − 2.5 + q + −12 = 7.8 q = e) 1 1 + r + − = −2 3 9 f) r = g) − 1.3 + t + −2.4 = −10 t = 1 3 − + s + = 0 5 8 s = h) 7.45 + −12.8 + u = 15 u = i) 3 1 − v + + = 0 4 6 v = 63 ¿Cómo restamos números con signo? También podemos hacer restas con números negativos. Por ejemplo, haz en tu calculadora la siguiente operación 9 – –8. Nota que el primer signo menos “–“ es el que se usa para restar, y que el segundo signo (–) es el que se utiliza para escribir números negativos en la calculadora. 9. ¿Qué resultado da la calculadora cuando haces la operación 9 – –8 __________________ ¿Por qué crees que se obtiene ese resultado? _______________________________________ ___________________________________________________________________________ 10. Teclea en la calculadora la expresión 10 – –6 y luego presiona la tecla ENTER. ¿Qué resultado da la calculadora? _______ ¿Qué crees que hace la calculadora cuando tecleas, uno en seguida del otro, los dos signos para la expresión “menos”? _____________________ 11. Realiza las siguientes operaciones usando la calculadora. j) 9 – –10 = m) 1/3 – – 1/3 = k) 14 – –14 = l) ½ – – ½ = n) –18 – – 14 = o) –100 – – 48 = 12. Explica qué operaciones realiza la calculadora para restar un número negativo. __________________________________________________________________________________ ____________________________________________________________________ 13. Encuentra el número que falta. Usa la calculadora para verificar tus respuestas. a) 4 – a =10 1 3 1 1 c) − − c = b) − − b = a = 2 4 3 2 b = c = d) –18 – d = 20 d = e) –40 – e = 50 e = f) 16 – f = 40 f = g) –17.5 – g = –19.4 g = h) 38.7 – h = 62.4 h = i) –17.9 – k = 100 k = 14. En el laboratorio de química un alumno observó que cada 60 segundos la temperatura de una sustancia disminuía la misma cantidad de grados. Al iniciar el experimento la temperatura de esa sustancia era 36 °C y seis minutos después era 24 °C. En otro experimento el alumno observó que otra sustancia tenía una temperatura de –30 °C y que aumentaba 4 °C cada minuto. Si él inició los dos experimentos al mismo tiempo, ¿después de cuántos minutos las dos sustancias tendrán la misma temperatura? ____________________________________ ¿Cuál es esa temperatura? ______________ _________________________________ 64 ¿Sirven para algo los números con signo? 1. Escribe una suma de números con signo que corresponda a cada una de las siguientes situaciones. a) En una ciudad la temperatura a las 10 de la noche era de 16°C. A partir de esa hora la temperatura disminuyó 1°C cada 10 minutos. ¿Cuál era la temperatura a las 5:00 AM del día siguiente? ________________________________________ ____________________________________ b) Un equipo de fútbol americano perdió 2 yardas en la primera oportunidad, en la segunda oportunidad ganó 7 yardas, en la tercera logró cero yardas, y en la última perdió 9 yardas. ¿Cuál fue el resultado de sus intentos en las cuatro oportunidades? ___________________________________ c) Colón descubrió América en 1492. Roma fue fundada 2 275 años antes. ¿En qué año tuvo lugar la fundación de Roma? ____________________________ ________________________________ d) Completa el siguiente cuadrado escribiendo en cada espacio uno de los siguientes números: –13, –10, –7, –4, 2, 5, 8 y 11. La condición que debe cumplir tu cuadrado mágico es que cualesquiera tres números colocados en línea recta deben sumar lo mismo. –1 65 A ddiivviinnaa qquuéé eessttaa ppaassaannddoo … …… …… …..… …… …… …… …… …… …… …… …… ….. Probabilidad Abre el archivo Adivdond.xls. Presiona la tecla F9 nueve veces, y en cada una observa lo que pasa. Si te fijas, los contadores te indican cuántas veces le ha tocado a cada uno de los tres tubos. El Total de tiros debe tener ahora el valor 10 (si te pasaste, puedes empezar de nuevo, cerrando tu archivo sin guardarlo y abriéndolo de nuevo). Copia los valores que obtuviste de cada contador en la tabla siguiente: TOTAL DE TIROS CONTADOR 1 CONTADOR 2 CONTADOR 3 10 Compara estos valores con los de otro equipo de trabajo. ¿Son iguales? ___________________________ ¿Por qué? _____________________________________________________________________________ Tu tarea es investigar cuál de los tres tubos tiene mayor probabilidad de que le toque y cuál tiene menor probabilidad. Para esto, sigue presionando la tecla F9 hasta que llegues a 100 tiros en total. Llena la tabla con tus valores obtenidos. TOTAL DE TIROS CONTADOR 1 CONTADOR 2 CONTADOR 3 10 ¿Cuál es el más probable? ________________________________________________________________ ¿Cuál es el menos probable? ______________________________________________________________ Compara con otro equipo. Una de las razones por las que hay que observar y experimentar con un fenómeno es la de poder predecirlo. ¿Podrías predecir qué valores tendrán los contadores al llegar a 1000 tiros? Trata de dar los valores que creas saldrán. MIS PREDICCIONES SON TOTAL DE TIROS CONTADOR 1 CONTADOR 2 CONTADOR 3 100 66 Adivina qué está pasando . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Ahora llega a los 1000 tiros (para esto, deja apretada la tecla F9 para ir más rápido y suéltala cuando estés cerca de los 1000 tiros). Escribe abajo los valores obtenidos. VALORES OBTENIDOS TOTAL DE TIROS CONTADOR 1 CONTADOR 2 CONTADOR 3 1000 Compara tus valores obtenidos con tus predicciones y con los valores de otros equipos. ¿Qué puedes concluir? __________________________________________________________________ _____________________________________________________________________________________ _____________________________________________________________________________________ No sólo es importante poder decir qué es más probable que suceda y qué es menos probable. También conviene dar números que indiquen esta probabilidad. Tu tarea ahora es decir qué tan probable es que le toque a cada uno de los tubos. ¿Cómo?, tienes que decidir (si tienes tiempo, puedes llegar ahora hasta 10 000 tiros en total y observar las proporciones). Escribe tus conclusiones y coméntalas con tus compañeros. ______________________________ _____________________________________________________________________________________ _____________________________________________________________________________________ _____________________________________________________________________________________ _____________________________________________________________________________________ _____________________________________________________________________________________ _______________________________________________________________________________ 67 ¿ PPoorr ddoonnddee ssaallddrráá ??… …… …… …… …… …… …..… …… …… …… …… …… …… …… …… ….. Probabilidad Imagina una caja piramidal como la que aparece a continuación. En su parte superior se tira una pelota y la caja se agita horizontalmente una y otra vez hasta que la pelota sale por alguna de las salidas de abajo: A, B, C, D, E o F. En la figura se muestra una posible trayectoria de la pelota. Cada vez que la pelota se encuentra en un nivel, tiene la misma probabilidad de caer a la izquierda o a la derecha. ¿Crees que la pelota tiene la misma probabilidad de llegar a todas las salidas (A, B, C, D, E o F)?__ _____________________________________________________________________________________ ¿Cuáles salidas crees que son las más probables? _____________________________________________ ¿Cuáles salidas crees que son las menos probables? ___________________________________________ Discute estas preguntas con tus compañeros. La probabilidad de que algo ocurra se mide con un número entre cero y uno. Por ejemplo, al tirar una moneda decimos que la probabilidad de que salga Sol es 1/2 o 0.5 o 50%. ¿Una probabilidad de 0.2 equivale a la fracción? ________________________o ¿a un porcentaje de? ___________________ %. Esto significa que 1 en cada 5, ocurrirá este evento. En cada nivel, ¿cuál es la probabilidad de que la pelota caiga a la izquierda? __________________________y ¿a la derecha? ___________________________________________ 68 • ¿Por dónde saldrá? . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Abre ahora la hoja ADIVDON2.XLS, la cual simula la situación anterior. Cada vez que presiones la tecla F9 se tira otra pelota y las celdas azules llevan la cuenta. Las celdas violetas dan la frecuencia de pelotas que llegan a esa salida. Presiona la tecla F9 varias veces hasta llegar a un total de 10 (si te pasas, tendrás que abrir de nuevo la hoja). ¿Observaste cómo la trayectoria de la pelota cambia cada vez? Anota en la tabla siguiente las cantidades y las frecuencias obtenidas. Cantidades Frecuencias A Total = 10 B C D E F Comprueba que cada frecuencia se obtiene dividiendo la cantidad respectiva entre el total. Presiona ahora la tecla F9 hasta llegar a un total de 100. Anota en la tabla siguiente las cantidades y las frecuencias obtenidas. Cantidades Frecuencias A Total = 100 B C D E F De acuerdo con estas observaciones, ¿cuáles salidas son más probables? __________________________ _____________________________________________________________________________________ ¿Cuáles salidas son menos probables? ______________________________________________________ Sigue presionando la tecla F9 hasta llegar a un total de 500. Anota en la tabla siguiente las cantidades y las frecuencias obtenidas. Cantidades Frecuencias A Total = 500 B C 69 D E F . . . . . .. . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .Probabilidad ¿Siguen siendo las salidas C y D las más probables y las salidas A y F las menos probables? ______ _____________________________________________________________________________________ En realidad, por la simetría de la caja, esperaríamos que las salidas C y D tengan el mismo número, pero por ser un proceso aleatorio, esto no sucede exactamente. También esperaríamos que las salidas _________________ y _______________ tengan el mismo número y que las salidas _______________ y ______________ tengan el mismo número. o. Ahora queremos deducir cuánto más probables son las salidas C y D que las salidas B y E. Observa tus datos de la tabla anterior y elige la más acertada de las tres opciones dadas. Las salidas C y D son 2, 3 o 4 veces más probables que las salidas B y E. Observa tus datos y contesta: Las salidas C y D son _________________________veces más probables que las salidas A y F. Una buena actividad es sumar los resultados de la última tabla de 10 o 20 grupos de trabajo para tener un total de 5000 o 10000 observaciones. Con esto podemos confirmar las respuestas a las preguntas anteriores. Un ratón de laboratorio entra en un laberinto como el representado en la figura siguiente. Discute la probabilidad que tiene de llegar a cada una de las salidas. Proyecto (difícil): El archivo ADIVDON2.XLS tiene una segunda hoja (Hoja1) con una caja más grande. Realiza el mismo trabajo que hicimos en esta hoja de trabajo pero con el modelo más grande. 70 Variación Reciproca I Mediante esta actividad vamos a identificar la diferencia entre proporcionalidad directa e inversa La proporcionalidad directa es una relación entre magnitudes medibles. Es uno de los escasos conceptos matemáticos ampliamente difundido en la sociedad. Esto La proporcionalidad directa es un caso particular de las variaciones lineales. El factor constante de proporcionalidad puede utilizarse para expresar la relación entre cantidades. Haciendo uso de la hoja de cálculo, modelar el siguiente problema: La receta de un pastel de vainilla indica que para cuatro personas se necesitan 200 g de harina, 150 de mantequilla, cuatro huevos y 120 g de azúcar. ¿Cómo adaptar la receta para cinco personas? ¿Para una boda que se estima que tendrá 250 personas? ¿Para cualquier cantidad de personas? Personas Harina (grs) Mantequilla (grs) Huevos Azúcar (grs) 4 200 150 4 120 5 250 n Se dice que la cantidad de cada ingrediente es proporcional al número de personas y se representa esta situación mediante una tabla de proporcionalidad Dos magnitudes son inversamente proporcionales si su producto es constante. En este caso se dice que las magnitudes son inversamente proporcionales. Dicho de otra manera si una de las magnitudes aumenta, la otra disminuye; y si una de las magnitudes disminuye, la otra variable aumenta. Haciendo uso de la hoja de cálculo, modelar el siguiente problema: Se ha conseguido un autobús de 40 asientos para un grupo de primer grado. El autobús tiene un costo total para el curso. Si van los 30 alumnos de grupo “A”, cada uno deberá pagar $1,800. Pero si participan 25 alumnos, ¿cuánto debe pagar cada uno? Observa cómo se llega a la solución analítica para construir tu tabla en hoja de cálculo: Nº de alumnos 2 Cuota 30 $1,800 25 x 1 30 x = 25 1800 x= 30 • 1800 25 x = ________ (-) (+) Si van 25 alumnos, la cuota del viaje por cada uno será de $_________ Si son menos alumnos, la cuota aumenta, ya que el costo del autobús es fijo. Se trata de una relación inversamente proporcional. Encuentra también la tabla hasta llegar al extremo de que sólo vaya un alumno. 71 Variación Reciproca II Mediante esta actividad vamos a modelar problemas que tengan que ver con el concepto de inversamente proporcional, haciendo uso de Hoja de Cálculo 1.- Miguel desea comprar 20 litros de pintura para embellecer su casa. En la tienda le ofrecen botes de distintos tamaños. Utilizando botes de la misma capacidad ¿Cuántos botes utilizará Miguel para 20 litros de pintura? Completa la tabla para ayudarle Litros en cada bote 20 Cantidad de botes 1 10 5 4 2 1 Si observas la tabla: • ¿Qué sucede con la cantidad de botes al disminuir los litros de pintura? _______________________________________________________________ • ¿Qué sucede con los litros de pintura al aumentar la cantidad de botes? _______________________________________________________________ • Construye una gráfica con los datos de la tabla anterior. 2.- Los alumnos de un curso desean hacer una tardeada para colaborar con un hogar de ancianos. Para esto, los 30 alumnos, piensan organizarse en equipos con igual cantidad de integrantes. Si cada equipo debe recaudar la misma cantidad de dinero y como meta se propusieron reunir $18,000 entre todos. a) Completa la tabla con el monto que debe reunir cada equipo para cumplir la meta Nº de equipos Nº de alumnos por equipo Monto por cada equipo b) ¿Cuántos alumnos puede tener cada equipo? ______________________________ c) ¿Qué relación hay entre estas cantidades? ___________________________ d) Construye una gráfica con los datos de la primera y tercer columna de la tabla anterior 72 Media, Mediana y Moda En esta secuencia analizaremos tres Medidas de tendencia central. Conforme vayas leyendo, compruébalo con una hoja de cálculo aplicando las funciones PROMEDIO (Media), MEDIANA Y MODA, respectivamente. La media es la suma de todos los valores de una variable dividida entre el número total de datos de los que se dispone. Como ejemplo: Consideremos 10 pacientes de edades 21, 32, 15, 59, 60, 61, 64, 60, 71, y 80 años. La media de edad de estos sujetos será de: x= 21 + 32 + 15 + 59 + 60 + 61 + 64 + 60 + 71 + 80 = 52.3años 10 Otra medida de tendencia central que se utiliza habitualmente es la mediana. Es la observación equidistante de los extremos. La mediana del ejemplo anterior sería el valor que deja a la mitad de los datos por encima de dicho valor y a la otra mitad por debajo. Si ordenamos los datos de menor a mayor observamos la secuencia: 15, 21, 32, 59, 60, 60,61, 64, 71, 80. Como quiera que en este ejemplo el número de observaciones es par (10 individuos), los dos valores que se encuentran en el medio son 60 y 60. Si realizamos el cálculo de la media de estos dos valores nos dará a su vez 60, que es el valor de la mediana. Si la media y la mediana son iguales, la distribución de la variable es simétrica. La media es muy sensible a la variación de las puntuaciones. Sin embargo, la mediana es menos sensible a dichos cambios. Por último, otra medida de tendencia central, no tan usual como las anteriores, es la moda, siendo éste el valor de la variable que presenta una mayor frecuencia. En el ejemplo anterior el valor que más se repite es 60, que es la moda. Otro ejemplo Se escogió un salón de clases de primer grado, con un total de 25 estudiantes, y se les pidió que calificaran del 1 al 5 a un programa televisivo. (5 = Excelente, 4 = Bueno, 3 = Regular, 2 = No muy bueno, 1 = Fatal) Estos fueron los resultados: 1, 3, 3, 4, 1, 2, 2, 2, 5, 1, 4, 5, 1, 5, 3, 5, 1, 4, 1, 2, 2, 1, 2, 3, 5 Buscar la media, la mediana y la moda e indicar si es muestra o población. 73 Jugando con las calificaciones En esta actividad se pretende que se realice una simulación con las calificaciones obtenidas por un grupo de alumnos y el caso particular de un alumno. Modelar ambas situaciones mediante el uso de una hoja de cálculo Situación 1 Las calificaciones en la asignatura de Matemáticas de 39 alumnos de una clase vienen dadas por la siguiente tabla: Calificaciones 1 2 3 4 5 6 7 8 9 Número de alumnos 2 2 4 5 8 9 3 4 2 Determinar: Media mediana moda También sin modificar las calificaciones de los alumnos que obtuvieron calificación menor a seis, se puede obtener un promedio mayor o igual a 8.5 Calificaciones 1 2 3 4 5 Número de alumnos 2 2 4 5 8 6 7 8 9 Situación 2 Un alumno de primer grado hasta el cuarto bimestre ha obtenido las siguientes calificaciones en español, sabemos que la calificación mínima es 5 y la máxima es 10 y sólo se asientan calificaciones enteras: Bimestre 01 02 03 04 Calificación 5 6 7 6 05 Promedio ¿Cuál es el promedio mínimo que puede obtener ya con los cinco bimestres? ____ ¿Cuál es el promedio máximo que puede obtener ya con los cinco bimestres? _____ ¿Cuál es la calificación que debe obtener en el quinto para tener un promedio de 7.5?______________________________________________________________________ 74 BIBLIOGRAFIA EMAT. (2000). Enseñanza de las matemáticas con Tecnología. Matemáticas con la hoja de cálculo. México: SEP. EMAT. (2000). Enseñanza de las matemáticas con Tecnología. Geometría dinámica. México SEP. EMAT. (2000). Enseñanza de las matemáticas con Tecnología. De los números al algebra en secundaria con el uso de la calculadora. México: SEP. EMAT. (2005). Enseñanza de las matemáticas con Tecnología. Programación computacional para matemáticas de secundarias. México: SEP. SEP. (2006). Programas de estudios 2006. Matemáticas. Educación básica. Secundaria. México: SEP. SEP. (2006). Fichero de actividades didácticas. Matemáticas. Educación secundaria, 2a ed., México. SEP. (2006). Secuencia y organización de contenidos. Matemáticas Educación secundaria, 2a ed., México. SEP. (2006). Libro para el maestro. Matemáticas. Secundaria, México. 75 DIRECTORIO Dra. Rocío Ruiz de la Barrera Secretaria de la S.E.P.H. Lic. José Fermín Garrido Baños Subsecretario de Educación Básica y Normal. Mtro. Pablo Moreno Calva Director General de Educación Básica Profr. Francisco Torres Ferra Subdirector de Secundarias Generales Profra. Elvia Licona Mejía Subdirectora de Telesecundarias Profr. José Valdemar García Sánchez Subdirector de Secundarias Técnicas Profra. Ma. Guadalupe Flores Barrera y Profr. Andrés Rivera Díaz Coordinadores Estatales del Proyecto Enseñanza de las Matemáticas con Tecnología, propuesta Hidalgo (EMAT-Hidalgo) Asesores externos Dra. Teresa Rojano Ceballos Coordinación General de Enseñanza de las Matemáticas con Tecnología Dra. Ana Isabel Sacristán Rock Investigadora Titular del Departamento de Matemática Educativa del Centro de Investigación y de Estudios Avanzados del IPN