Lugares geométricos. Cónicas.

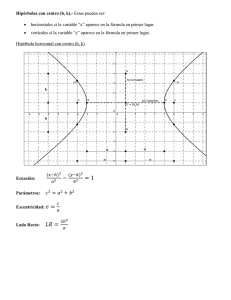
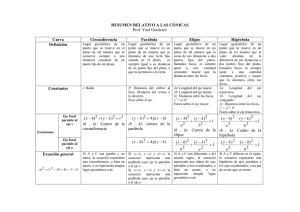
LUGARES GEOMÉTRICOS
Un lugar geométrico es el conjunto de puntos del plano que cumplen una determinada condición
geométrica, que se traduce en una ecuación algebraica. Un lugar geométrico es la ecuación que
satisfacen el conjunto de sus puntos.
LAS CÓNICAS
CIRCUNFERENCIA
Una circunferencia es el lugar geométrico de los puntos del plano que se encuentran a una
distancia fija llamada radio, de un punto dado, llamado centro.
ECUACIÓN DE LA CIRCUNFERENCIA
Considérese la circunferencia centrada en O = (a, b) y de radio r. La condición para que un punto
X = (x, y) se encuentre en la misma es, d (X, O) = r, es decir:
( x − a ) 2 + ( y − b) 2 = r
o
(x – a)2 + (y – b)2 = r2
Desarrollando los cuadrados se tiene:
x2 – 2ax + a2 + y2 – 2by + b2 = r2
x2 + y2 – 2ax – 2by + a2 + b2 – r2 = 0
Llamando A = –2a, B = –2b y C = a2 + b2 – r2, se tiene:
x2 + y2 + A x + B y + C = 0

CÁLCULO DE LOS ELEMENTOS DE UNA CIRCUNFERENCIA
La ecuación de una circunferencia con centro en (a, b) y radio r es:
x2 + y2 + A x + B y + C = 0
donde: A = –2a, B = –2b y C = a2 + b2 – r2.

POTENCIA DE UN PUNTO RESPECTO DE UNA CIRCUNFERENCIA
Considérese una circunferencia cualquiera y un punto P del plano. Desde el punto P se trazan dos
secantes a la circunferencia, obteniéndose los puntos A, A', B y B'.
PA · PB = PA’ · PB’
El valor común PA · PB = PA’ · PB’ recibe el nombre de potencia del punto P respecto de la
circunferencia dada.
La potencia de un punto P respecto de una circunferencia es igual al cuadrado de la distancia del
punto al centro de la circunferencia, d2, menos el cuadrado del radio de la circunferencia:
PA · PB = d2 – r2
Sea O el centro de la circunferencia. La recta que une P con O, corta a la circunferencia en A y en
B.
Llamando d a la distancia PO y r al radio de la circunferencia, se tiene que PA = d – r y PB = d + r
La potencia es entonces: PA · PB = (d – r) · (d + r)
Obsérvese que la potencia, dependiendo de la posición del punto P respecto a la circunferencia,
toma los valores:
•
Positivo, si P es un punto exterior a la circunferencia (d > r)
•
Cero, si P es un punto de la circunferencia (d = r)
•
Negativo, si P es un punto interior a la circunferencia (d > r).
EXPRESIÓN ANALÍTICA DE LA POTENCIA DE UN PUNTO RESPECTO DE UNA
CIRCUNFERENCIA
La ecuación de una circunferencia es x2 + y2 + Ax + By + C = 0; el primer miembro se obtuvo
elevando al cuadrado la distancia de un punto al centro de la circunferencia y restando el cuadrado
del radio, es decir, hallando la potencia del punto respecto de la circunferencia.
Así pues, para calcular la potencia de un punto respecto de una circunferencia, basta con sustituir
las coordenadas del punto en el primer miembro de la ecuación de la circunferencia.
EJE RADICAL
Se llama eje radical de dos circunferencias al lugar geométrico de los puntos que tienen la misma
potencia respecto de ambas.
El eje radical de dos circunferencias es una recta perpendicular a la recta que une sus centros.
CÁLCULO ANALÍTICO DEL EJE RADICAL DE DOS CIRCUNFERENCIAS
Sean dos circunferencias de ecuaciones:
C1 = x2 + y2 + Ax + By + C = 0
y
C2= x2 + y2 + A’x + B ’y + C ‘ = 0
Su eje radical es el lugar geométrico de los puntos que tienen la misma potencia respecto de ambas.
Dichas potencias son:
PotC1 ( P ) = x2 + y2 + Ax + By + C
y
PotC2 ( P) = x2 + y2 + A’x + B ’y + C ‘
La ecuación del lugar geométrico es:
x2 + y2 + Ax + By + C = x2 + y2 + A’x + B’y + C’
(A – A’) x + (B – B’) y + (C – C ’) = 0
CENTRO RADICAL DE TRES CIRCUNFERENCIAS
Se llama centro radical de tres circunferencias, cuyos centros no estén alineados, al punto que
tiene la misma potencia respecto de las tres.
Como los centros no están alineados, si se consideran dos de los ejes radicales, éstos no serán
paralelos y tendrán un único punto de intersección. Dicho punto es el centro radical de las tres
circunferencias.
LA PARÁBOLA
Una parábola es el lugar geométrico de un punto que se mueve en un plano de tal
manera que su distancia a una recta fija, situada en el plano, es siempre igual a su distancia a
un punto fijo del plano que no pertenece a la recta.
El punto fijo se denomina foco y la recta fija directriz de la parábola. Tal como puede
observarse en la figura, designemos por F y d el foco y la directriz de una parábola,
respectivamente. La recta a que pasa por F y es perpendicular a d se denomina eje de la parábola.
Sea A el punto de intersección del eje y la directriz. El punto V, punto medio del segmento AF está,
por definición, sobre la parábola. Este punto se llama vértice de la parábola. El segmento de recta,
tal como BB’, que une dos puntos cualesquiera diferentes de la parábola se llama cuerda. En
particular, una cuerda que pasa por el foco, como CC ’, se denomina cuerda focal. La cuerda focal
LL’ perpendicular al eje se llama lado recto. Si P es un punto cualquiera de la parábola, la recta FP
que une el foco F con el punto P se llama radio focal de P o radio vector.
ECUACIONES DE LA PARÁBOLA
La ecuación de una parábola adopta su forma más simple cuando su vértice está en el origen
y su eje coincide con uno de los ejes coordenados.
Tal como puede observarse en la figura, consideremos la parábola cuyo vértice está en el
 p
origen y cuyo eje coincide con el eje Y. El foco F está sobre el eje Y. Sean  0,  , sus
 2
coordenadas.
Por definición de parábola, la ecuación de la directriz d es y = −
p
.
2
Sea P(x, y) un punto cualquiera de la parábola. Tracemos por P el segmento PA
perpendicular a d. Entonces, por la definición de parábola. el punto P debe satisfacer la condición:
| FP | = | PA |
Ahora bien,
| FP | =
pero como
x2 + (y −
p 2
)
2
| PA | = | y +
p
|
2
tendremos:
x2 + (y −
p
p 2
) =|y+ |
2
2
Elevando al cuadrado ambos miembros de esta última ecuación y simplificando, se obtiene
x2 = 2py
Si el vértice de la parábola está en el origen y su eje coincide con el eje X, se demuestra que
la ecuación de la parábola es:
y2 = 2px
p 
en donde el foco es el punto  , 0  .
2 
De una manera más general tenemos que:
La ecuación de una parábola de vértice (h, k) y eje paralelo al eje Y, es de la forma:
(x – h)2 = 2p (y – k)
siendo p el parámetro (distancia desde el foco F a la directriz d).
Si el vértice es el punto (h, k) y eje paralelo al eje X, su ecuación es de la forma:
(y – k)2 = 2p (x – h)
siendo p el parámetro (distancia desde el foco F a la directriz d).
LA ELIPSE
Una elipse es el lugar geométrico de un punto que se mueve en un plano de modo que
la suma de sus distancias a dos puntos fijos de ese plano es siempre igual a una constante,
mayor que la distancia entre los dos puntos.
Los dos puntos fijos se denominan focos de la elipse. Tal como puede observarse en la
figura, sean F y F‘ los focos de una elipse. La recta r que pasa por los focos recibe el nombre de eje
focal.
El eje focal corta a la elipse en dos puntos, A y A’, que se denominan vértices. La porción
del eje focal comprendida entre los vértices, es decir, el segmento AA’, se llama eje mayor. El
punto C del eje focal, punto medio del segmento que une los focos, se denomina centro. La recta r’
que pasa por C y es perpendicular al eje focal r, recibe el nombre de eje normal. El eje normal
r‘corta a la elipse en dos puntos, B y B’, y el segmento BB’ se denomina eje menor. Un segmento
como BU que une dos puntos diferentes cualesquiera de la elipse, se llama cuerda. Una cuerda que
pasa por uno de los focos se denomina cuerda focal. Una cuerda que pasa por el centro C se
denomina diámetro. Si P es un punto cualquiera de la elipse, los segmentos FP y F ’P que unen los
focos con el punto P se llaman radios vectores de P.
ECUACIONES DE LA ELIPSE
Tal como puede observarse en la figura, consideremos la elipse de centro en el origen y
cuyo eje focal coincide con el eje X.
Los focos F y F ‘ están sobre el eje X. Como el centro O es el punto medio del segmento
FF ‘, las coordenadas de F y F ‘ serán (c, 0) y (–c, 0) respectivamente, siendo c una constante
positiva.
Sea P = (x, y) un punto cualquiera de la elipse. El punto P debe satisfacer la ecuación
| FP | + | F ’P | = 2a
siendo a una constante positiva mayor que c.
Ahora bien,
| FP | =
( x − c) 2 + y 2
| F ’P | =
( x + c) 2 + y 2
de modo que la condición geométrica queda expresada analíticamente por la ecuación:
( x − c) 2 + y 2 +
( x + c) 2 + y 2 = 2a
Para simplificar la ecuación anterior, pasamos el segundo radical al segundo miembro,
elevamos al cuadrado, simplificamos y agrupamos los términos semejantes. De este modo se
obtiene:
cx + a2 = a
( x + c) 2 + y 2
Elevando de nuevo al cuadrado, resulta:
c2x2 + 2a2cx + a4 = a2x2 + 2a2cx + a2c2 + a2y2
de donde
(a2 – c2) x2 + a2y2 = a2(a2 – c2)
Como 2a > 2c se cumple que a2 > c2 y, por lo tanto, (a2 – c2) es un número positivo que
puede ser reemplazado por el número positivo b2,es decir,
b2 = a2 – c2
Sustituyendo a2 – c2 por b2, se obtiene
b2x2 + a2y2 = a2b2
Dividiendo por a2b2 resulta
x2 y2
+
=1
a2 b2
Por ser a y –a las intersecciones con el eje X, las coordenadas de los vértices A y A’ son
(a, 0) y (–a, 0) respectivamente, y la longitud del eje mayor es igual a 2a.
Las intersecciones con el eje Y son b y – b. Por lo tanto, las coordenadas de los vértices B y
B’ del eje menor son (0, b) y (0, –b) respectivamente, y la longitud del eje menor es igual a 2b.
Así pues, la elipse es simétrica con respecto a ambos ejes coordenados y al origen.
Se define la excentricidad de una elipse como la razón
e. Así pues:
e=
c
a2 − b2
=
a
a
c
y se suele representar con la letra
a
Como c < a, la excentricidad de una elipse es menor que uno.
Si consideramos ahora el caso en que el centro de la elipse está en el origen, pero su eje
focal coincide con el eje Y. Las coordenadas de los focos son entonces (0, c) y (0, –c). En este caso,
la ecuación dela elipse es
y2 x2
+
=1
a2 b2
en donde a es la longitud del semieje mayor, b la longitud del semieje menor y a2 = b2 + c2.
De una manera más general tenemos que:
La ecuación de una elipse de centro (h, k) y eje focal paralelo al eje X, viene dada por
la expresión:
( x − h) 2 ( y − k ) 2
+
=1
a2
b2
La ecuación de una elipse de centro (h, k) y eje focal paralelo al eje Y, viene dada por
la expresión:
( y − k ) 2 ( x − h) 2
+
=1
a2
b2
Para cada elipse, a es la longitud del semieje mayor, b es la longitud del semieje menor,
c es la distancia del centro a cada foco, y a, b y c están ligados por la expresión a2 = b2 + c2.
LA HIPÉRBOLA
Una hipérbola es el lugar geométrico de un punto que se mueve en un plano de modo
que el valor absoluto de la diferencia de sus distancias a dos puntos fijos del plano, llamados
focos, es siempre igual a una cantidad constante, positiva y menor que la distancia entre los
focos.
Tal como puede observarse en la figura, los focos se designan por F y F ‘. La recta r que
pasa por los focos recibe el nombre de eje focal. El eje focal corta a la hipérbola en dos puntos A y
A’, denominados vértices. La porción del eje focal comprendido entre los vértices, el segmento
AA’, se llama eje transverso. El punto medio C del eje transverso se denomina centro. La recta r’
que pasa por C y es perpendicular al eje focal r recibe el nombre de eje normal. El eje normal r' no
corta a la hipérbola. La porción del eje normal, el segmento BB’, que tiene C por punto medio, se
denomina eje conjugado. El segmento que une dos puntos distintos cualesquiera de la hipérbola se
llama cuerda. Una cuerda que pasa por un foco, recibe el nombre de cuerda focal. Una cuerda que
pasa por C, se llama diámetro. Si P es un punto cualquiera de la hipérbola, los segmentos FP y
F ‘P que une los focos con el punto P se denominan radios vectores de P.
ECUACIONES DE LA HIPÉRBOLA
Tal como puede observarse en la figura, consideremos la hipérbola de centro en el origen y
cuyo eje focal coincide con el eje X.
Los focos F y F ‘ están situados sobre el eje X. Como el punto C es el punto medio del
segmento FF ‘, las coordenadas de F y F ‘ serán, respectivamente, (c, 0) y (–c, 0) siendo c una
constante positiva.
Sea P = (x, y) un punto cualquiera de la hipérbola. Por la definición de hipérbola, el punto P
debe satisfacer la condición
| | FP | – | F ’P | | = 2a
en donde a es una constante positiva y 2a < 2c. La condición geométrica es equivalente a las
dos relaciones
| FP | – | F ’P | = 2a
| FP | – | F ’P | = –2a
La primera de estas relaciones se verifica cuando P está sobre la rama izquierda de la
hipérbola. La segunda relación se verifica cuando P está sobre la rama derecha.
Ahora bien,
| FP | =
( x − c) 2 + y 2
| F ’P | =
( x + c) 2 + y 2
de modo que la condición geométrica queda expresada analíticamente por
( x − c) 2 + y 2 –
( x + c) 2 + y 2 = 2a
Procediendo de forma análoga a como lo hicimos en la elipse, la ecuación precedente se
reduce a
(c2 – a2) x2 – a2y2 = a2 (c2 – a2)
Puesto que c > a, (c2 – a2) es un número positivo que podemos designar por b2. Por
consiguiente, sustituyendo en la ecuación anterior la relación
b2 = c2 – a2
se obtiene
b2x2 – a2y2 = a2b2
que puede escribirse en la forma
x2 y2
−
=1
a2 b2
Las intersecciones de la hipérbola considerada con el eje X son a y –a. Por consiguiente, las
coordenadas de los vértices A y A’ son (a, 0) y (–a, 0) respectivamente, y la longitud del eje
transverso es igual a 2a. Aunque no hay intersecciones con el eje Y, se toman como extremos del
eje conjugado los puntos B = (0, b) y B’ = (0, –b). Por lo tanto, la longitud del eje conjugado es
igual a 2b.
La hipérbola es simétrica respecto a ambos ejes coordenados y al origen.
La excentricidad e de una hipérbola está definida por la razón
e=
c
. Así pues,
a
c
a2 + b2
=
a
a
Como c > a, la excentricidad de una hipérbola es mayor que la unidad. Si el centro de la
hipérbola está en el origen pero su eje focal coincide con el eje Y, se demuestra análogamente, que
la ecuación de la hipérbola es
y2 x2
−
=1
a2 b2
De una manera más general, si el centro de la hipérbola no está en el origen de coordenadas,
pero sus ejes son paralelos a los ejes coordenados, se obtiene el siguiente resultado:
La ecuación de la hipérbola de centro el punto (h, k) y eje focal paralelo al eje X, es de
la forma
( x − h) 2 ( y − k ) 2
−
=1
a2
b2
Si el eje focal es paralelo al eje Y, su ecuación es
( y − k ) 2 ( x − h) 2
−
=1
a2
b2
Para cada hipérbola, a es la longitud del semieje transverso, b la longitud del semieje
conjugado, c la distancia del centro a cada foco y a, b y c están ligados por la relación
c2 = a2 + b2
La excentricidad viene dada por la relación
e=
c
a2 + b2
>1
=
a
a
ASÍNTOTAS DE LA HIPÉRBOLA
Si en la ecuación de la hipérbola b2x2 – a2y2 = a2b2 despejamos y, se obtiene
y=±
b
x2 − a2
a
y=±
bx
a2
1− 2
a
x
que puede escribirse del modo siguiente
Si un punto de la hipérbola se mueve a lo largo de la curva, de manera que su abscisa x
aumente ilimitadamente, el radical del segundo miembro de la ecuación anterior se aproxima cada
vez más a la unidad y la ecuación tiende a la forma
y=±
bx
a
Como la ecuación anterior representa las rectas y =
bx
bx
y y = − , la hipérbola es asíntota
a
a
a estas dos rectas.
HIPÉRBOLA EQUILÁTERA
Consideremos ahora la hipérbola cuyos ejes transverso y conjugado son de igual longitud.
Entonces a = b, y la ecuación b2x2 – a2y2 = a2b2 toma la forma
x2 – y2 = a2
Debido a que sus ejes son iguales, la hipérbola anterior recibe el nombre de equilátera. La
asíntotas de la hipérbola equilátera son las rectas x – y = 0 y x + y = 0. Como estas rectas son
perpendiculares, resulta que las asíntotas de una hipérbola equilátera son perpendiculares entre sí.
Una forma particularmente útil de la ecuación de la hipérbola equilátera es
a2
x· y =
2
A partir de la definición de hipérbola se obtiene:
Parámetros: a2 = 2xy;
a = b;
Focos: F ‘ = (–a, –a)
Vértices: A = ( a ,
a );
A ‘ = (– a , – a );
La excentricidad es constante e igual a
c=a 2
F = (a, a)
B = (– a ,
a );
B‘=( a,– a)
2.
Otros lugares geométricos
Lugar geométrico
Observaciones
Mediatriz de un segmento de
extremos A y B
d (A, P) = d (B, P)
Es una recta que corta perpendicularmente al
segmento por su punto medio.
Bisectriz de dos rectas
secantes
d (r, P) = d (s, P)
Dos rectas secantes tiene dos bisectrices
perpendiculares entre sí.