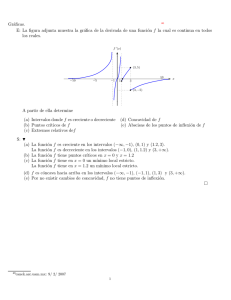
Gráficas. S - Canek
Anuncio
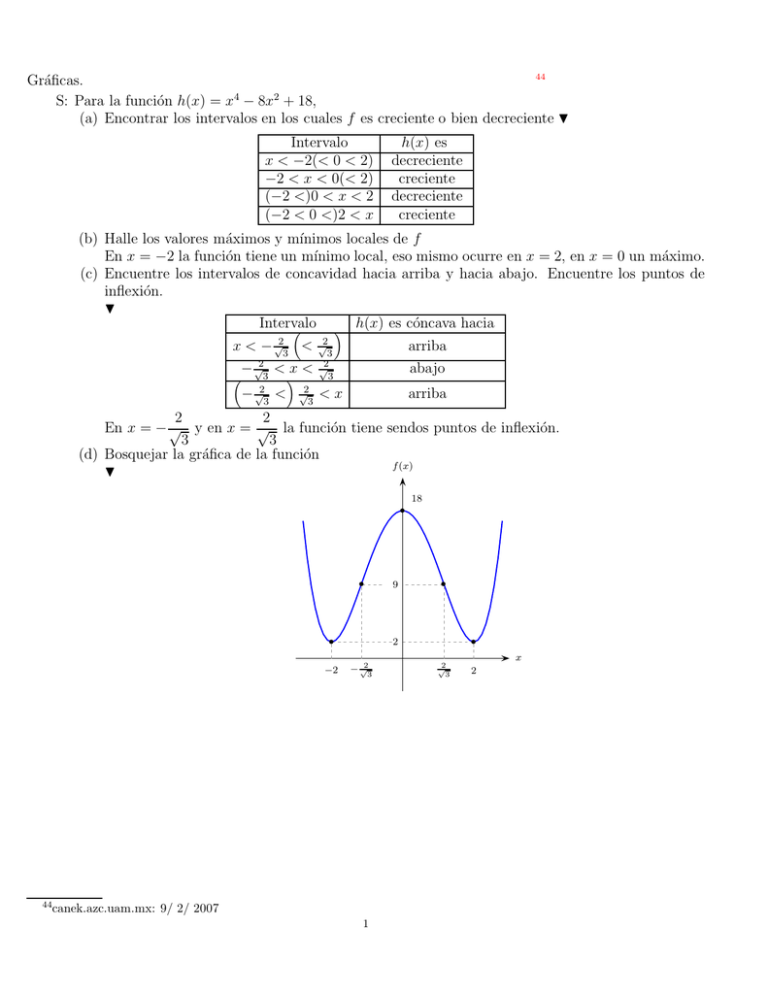
44 Gráficas. S: Para la función h(x) = x4 − 8x2 + 18, (a) Encontrar los intervalos en los cuales f es creciente o bien decreciente H Intervalo x < −2(< 0 < 2) −2 < x < 0(< 2) (−2 <)0 < x < 2 (−2 < 0 <)2 < x h(x) es decreciente creciente decreciente creciente (b) Halle los valores máximos y mı́nimos locales de f En x = −2 la función tiene un mı́nimo local, eso mismo ocurre en x = 2, en x = 0 un máximo. (c) Encuentre los intervalos de concavidad hacia arriba y hacia abajo. Encuentre los puntos de inflexión. H Intervalo h(x) es cóncava hacia 2 2 x < − √3 < √ 3 arriba − √2 < x < √23 3 − √23 < √23 < x abajo arriba 2 2 En x = − √ y en x = √ la función tiene sendos puntos de inflexión. 3 3 (d) Bosquejar la gráfica de la función f (x) H b b 9 b 18 b b 2 x −2 − √2 3 44 canek.azc.uam.mx: 9/ 2/ 2007 1 2 √ 3 2