CAPÍTULO 6 Efectos de Escala y Similitud Hidrológica

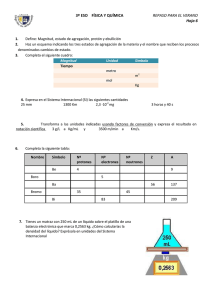
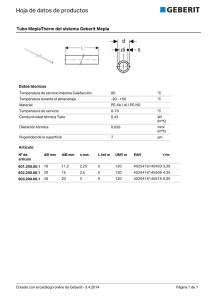
Tesis Doctoral: “Efectos de Escala sobre la Simulación del Flujo de Agua Superficial
en Áreas Urbanas Usando Modelos Basados en la Onda Cinemática”
Capítulo 6: Efectos de Escala y Similitud Hidrológica
6.1
CAPÍTULO 6
Efectos de Escala y Similitud Hidrológica
6.1.
EFECTOS DE ESCALA EN LA SIMULACIÓN DEL FLUJO DE AGUA SUPERFICIAL
La agregación de un esquema de modelación de ED implica que una subcuenca compleja,
compuesta por un conjunto de segmentos (planos de escurrimiento, cunetas y eventualmente,
canales y conductos), sea reemplazada por un único plano equivalente, PE (EA).
La agregación tiene dos componentes: geométrico y de procesos (fuente: del autor a los fines de
esta investigación).
6.1.1
Agregación geométrica
La agregación geométrica consiste en la modificación de la longitud típica de los planos. Con la
agregación, la longitud del PE, L EA , puede ser mayor o igual que la longitud media de los planos
de ED, L ED (calculada como promedio ponderado por superficie), de acuerdo al criterio que
adopte el modelista.
Conservando la rugosidad y pendiente de los planos entre ambas escalas, si se adopta L EA >
L ED , aumenta t p (5.50), por lo que el efecto de la agregación geométrica (EAG) es un atraso del
pico del hidrograma. En cambio, si se adopta L EA = L ED , t p no varía y EAG es nulo.
6.1.2
Agregación de procesos
La agregación de procesos consiste en la remoción de cunetas, canales y conductos de menor
jerarquía con el aumento de escala.
Todo componente de la red de drenaje incorpora almacenamiento a la misma y en consecuencia,
atenúa en algún grado el hidrograma de salida. Con la remoción de los segmentos mencionados
se produce una pérdida de almacenamiento, por lo que el efecto de la agregación de procesos
(EAP) es un anticipo del pico del hidrograma.
Los efectos individuales EAG y EAP actúan simultáneamente sobre el hidrograma simulado con
EA. El efecto de agregación neto (EAN) es igual a la suma de los efectos individuales:
EAN = EAG + EAP
(6.1)
EAN: efecto de agregación neto, EAG: efecto de agregación geométrica, EAP: efecto de agregación de
procesos.
EAG, EAP y EAN se pueden expresar por medio de la variación que introducen en algún
parámetro representativo de la respuesta hidrológica (por ej. en el tiempo de equilibrio). Si
predomina alguno de los efectos individuales, EAN no es nulo y se modifica la respuesta
hidrológica.
Ing. Raúl A. Pedraza
Tesis Doctoral: “Efectos de Escala sobre la Simulación del Flujo de Agua Superficial
en Áreas Urbanas Usando Modelos Basados en la Onda Cinemática”
Capítulo 6: Efectos de Escala y Similitud Hidrológica
6.2
A continuación se ejemplifican numéricamente los efectos de escala descritos.
Ejemplo Nº 6.1 (fuente: del autor a los fines de esta investigación).
Sea una cuenca urbana de 0.5 ha de superficie, compuesta por un tramo de calzada pavimentada
de 100 m de longitud, al que aportan 2 planos adyacentes, cada uno con una longitud media de
25m. Se asume que la cuenca es homogénea e impermeable, con el objeto de aislar del análisis:
a) efectos de heterogeneidades espaciales de parámetros físicos y b) efectos de atenuación
originados por pérdidas de escurrimiento.
Se consideraron 3 esquemas de modelación: un esquema de ED (A) y dos esquemas de EA (B y
C) (Figura Nº 6.1), los que se describen a continuación:
a)
Esquema A: compuesto por dos planos idénticos que aportan lateralmente a un segmento de
cordón cuneta doble (Figura Nº I.6, Anexo I). Los planos tienen una rugosidad N = 0.050, una
pendiente S = 1% y una longitud L = 25 m. El cordón cuneta tiene una rugosidad n = 0.015,
pendientes transversales del 3 %, una longitud de 100 m y una pendiente longitudinal del 1 %.
b)
Esquema B: consiste en un plano único, con una longitud de flujo de 100 m, con igual
rugosidad y pendiente que los planos del Esquema A.
c)
Esquema C: compuesto por un plano único, con igual longitud, rugosidad y pendiente que los
planos del Esquema A.
Figura Nº 6.1: Esquemas de modelación considerados (fuente: del autor, a los fines de esta
investigación).
Al pasar del esquema A al B ó C, se introducen efectos de escala en los resultados de la
simulación. Estos efectos fueron evaluados para una lluvia en exceso de intensidad constante
igual a 60 mm/h, a través de la variación que introducen en el tiempo de equilibrio y en los
hidrogramas simulados a la salida de cada esquema.
A partir de las ecuaciones (5.50) y (5.55) se calcularon t p y t c para los tres esquemas. Luego se
calcularon las variaciones ∆t p y ∆t c de los esquemas B y C respecto de A. Los resultados se
muestran en la Tabla Nº 6.1.
Ing. Raúl A. Pedraza
Tesis Doctoral: “Efectos de Escala sobre la Simulación del Flujo de Agua Superficial
en Áreas Urbanas Usando Modelos Basados en la Onda Cinemática”
Capítulo 6: Efectos de Escala y Similitud Hidrológica
6.3
Tabla Nº 6.1: Parámetros de los esquemas (fuente: del autor, a los fines de esta investigación).
Parámetro/
Variación
L
A
B
C
[m]
25
100
25
tp
[min]
6.2
14.2
6.2
∆t p
[min]
----
8.0
0.0
tc
∆t c
[min]
2.6
0.0
0.0
[min]
----
-2.6
-2.6
t e = tp + tc
[min]
8.8
14.2
6.2
∆ t e = ∆t p + ∆ t c
[min]
[%]
-------
5.4
62.1
-2.6
-29.5
L: longitud del plano, t p : tiempo de equilibrio del plano, t c : tiempo de equilibrio del canal, t e : tiempo de
equilibrio del esquema, ∆t p , ∆t c y ∆t e : variación de t p , t c y t e para una EA respecto de ED,
respectivamente.
Para el Esquema B, la agregación geométrica origina un aumento de t p (EAG = ∆t p = 8.0min), la
agregación de procesos introduce una disminución de t c (EAP = ∆t c = - 2.6 min) y el efecto neto
resultante es un aumento de t e (EAN = ∆t e = 5.4 min).
Para el Esquema C, la agregación geométrica no origina aumento de t p (EAG = ∆t p = 0), la
agregación de procesos introduce una reducción de t c (EAP = ∆t c = - 2.6 min) y el efecto neto
es una disminución de t e (EAN = ∆t e = - 2.6 min).
Se simularon los hidrogramas de salida de cada esquema por aplicación del modelo OCRED-1
(Pedraza, 2002). Este modelo se basa en las ecuaciones de onda cinemática y es una versión
actualizada del DURM (Deterministic Urban Runoff Model) (Schaake, 1971) (Anexo I).
Para ello, se consideraron 2 tormentas de igual intensidad de lluvia (i = 60 mm/h) pero distinta
duración ( t r ): 5 min y 30 min. Las duraciones se adoptaron menor y mayor a los t p de los planos
de EA, para evaluar los efectos de escala cuando se alcanzan los equilibrios cinemáticos parcial y
completo, respectivamente. Los hidrogramas simulados a la salida de cada esquema se
muestran en la Figura Nº 6.2.
El caudal máximo para la condición de equilibrio completo es igual al producto de la intensidad de
lluvia por el área de la cuenca (0.083 m3/s). Para este caudal, el ancho anegado de cada cuneta a
la salida (Esquema A) es de 2.1 m y el tirante es de 0.063 m.
Se puede observar que para la duración t r = 30 min se alcanza un equilibrio cinemático completo
para los tres esquemas y el caudal máximo es el mismo. Los efectos de escala sólo se
manifiestan en errores en el tiempo al pico de los hidrogramas simulados con EA.
En cambio, para la duración t r = 5 min se alcanza un equilibrio parcial en los planos de EA y la
agregación introduce errores tanto en el tiempo al pico como en el caudal pico de los hidrogramas
simulados con EA: para el Esquema B, el error del caudal máximo es por defecto, igual a –71.2 %
y para el Esquema C es por exceso, del 11.5%.
Ing. Raúl A. Pedraza
Tesis Doctoral: “Efectos de Escala sobre la Simulación del Flujo de Agua Superficial
en Áreas Urbanas Usando Modelos Basados en la Onda Cinemática”
Capítulo 6: Efectos de Escala y Similitud Hidrológica
6.4
Figura Nº 6.2: Hidrogramas simulados a la salida de los esquemas (fuente: del autor, a los fines
de esta investigación).
0.090
0.080
CAUDAL [m3/s]
0.070
0.060
0.050
0.040
0.030
0.020
0.010
0.000
0
5
10
ESCALA A (N = 0.050) - tr = 5 min
ESCALA B (N = 0.050) - tr = 5 min
ESCALA C (N = 0.050) - tr = 5 min
15
20
25
TIEMPO30[min]
ESCALA A (N = 0.050) - tr = 30 min
ESCALA B (N = 0.050) - tr = 30 min
ESCALA C (N = 0.050) - tr = 30 min
La probabilidad de ocurrencia de una condición de equilibrio parcial en un plano de EA es mayor
a medida que aumenta t p y disminuye t r (tormentas de corta duración).
En conclusión, los efectos de la agregación sobre los resultados de la simulación del flujo de agua
superficial se manifiestan en: a) errores en el tiempo al pico, si el plano de EA alcanza un
equilibrio cinemático completo y b) errores tanto en el tiempo al pico como en el caudal pico, si
dicho plano alcanza un equilibrio parcial.
6.2.
SIMILITUD HIDROLÓGICA
En esta Tesis, se denomina de este modo a la semejanza entre hidrogramas simulados con
esquemas topológicos de distinta escala.
Para mantener una similitud hidrológica entre escalas, es necesario conservar t e . Esto equivale a
anular EAN. Para ello, se debe recurrir al escalamiento de los parámetros.
Como se ha visto en el Capítulo 5, son tres los parámetros de un plano que influyen sobre sobre
t p : la rugosidad (N), la longitud (L) y la pendiente (S). En la expresión de t p (5.50), N y L están
elevados a un exponente 3 5 mientras que S lo está a 3 10 , por lo que t p es más sensible a las
variaciones de los dos primeros.
Por este motivo, los parámetros del flujo superficial que usualmente se escalan son la longitud y
el coeficiente de rugosidad, mientras que la pendiente se conserva entre escalas.
Existen dos posibles procedimientos para escalar N y L:
Ing. Raúl A. Pedraza
Tesis Doctoral: “Efectos de Escala sobre la Simulación del Flujo de Agua Superficial
en Áreas Urbanas Usando Modelos Basados en la Onda Cinemática”
Capítulo 6: Efectos de Escala y Similitud Hidrológica
6.5
a)
Adoptar la longitud del PE ( L EA ) como parámetro de calibración. Consiste en adoptar para
este plano la rugosidad media areal de los planos de ED y aumentar L EA respecto a L ED
hasta que EAG iguale a EAP (se anule EAN). Por medio del aumento de la longitud se
aumenta el almacenamiento, en un valor igual al perdido por remoción de los canales y
conductos de menor jerarquía.
Zaghloul (1981, 1983) y Huber et al. (1992) aplicaron este procedimiento para escalar el
modelo SWMM. Calcularon los parámetros físicos de los planos agregados (excepto la
longitud) como promedios ponderados por superficie. Para compensar la pérdida de
almacenamiento, aumentaron la longitud de los planos agregados por medio de la reducción
del parámetro ancho de cuenca (igual a la suma de los anchos de las subcuencas).
b)
Adoptar la rugosidad efectiva del PE ( N* ) como parámetro de calibración. Este parámetro
pasa a tener un significado computacional y deja de tener el significado físico de la rugosidad
de ED (Goodrich, 1990). Consiste en calcular L EA en base al mapa de la cuenca y luego
calibrar N* , de manera de anular EAN.
Goodrich (1990) aplicó este procedimiento para escalar el modelo KINEROS en cuatro
cuencas rurales de Arizona. Calculó los parámetros físicos del PE (incluida la longitud) como
promedios (ponderados por superficie) de los parámetros de ED y calibró la rugosidad
efectiva con el objeto de conservar el tiempo de respuesta característico del sector a agregar.
Si bien ambos procedimientos son válidos, en esta Tesis se adopta el segundo por considerarlo
con mayor sustento geométrico y físico.
Se describen a continuación los conceptos de base en los que se sustenta el procedimiento de
agregación propuesto en esta Tesis (Capítulo 8).
6.2.1.
Almacenamiento de Equilibrio
El almacenamiento de equilibrio ( S eq ) es el volumen de agua en tránsito hacia la salida de una
cuenca, sobre una superficie impermeable, bajo una lluvia espacial y temporalmente uniforme,
cuando se ha alcanzado el equilibrio cinemático completo (Wu et al., 1978).
En el caso de cuencas urbanas con sistema de drenaje dual, el volumen comprende no sólo el
agua que escurre superficialmente, sino también la que fluye a través de conductos subterráneos
(fuente: del autor, a los fines de esta investigación).
Es una poderosa medida de la función de respuesta de una cuenca, ya que integra los efectos de
la topografía, convergencia del flujo y rugosidad hidráulica. Es la “llave” del escalamiento de los
parámetros, ya que conservando S eq se conserva t e y por lo tanto, una similitud hidrológica
entre escalas.
Dividiendo (5.42) sobre (5.40) se obtiene la relación entre el tirante del flujo sobre el plano y la
distancia hacia aguas abajo:
Ing. Raúl A. Pedraza
Tesis Doctoral: “Efectos de Escala sobre la Simulación del Flujo de Agua Superficial
en Áreas Urbanas Usando Modelos Basados en la Onda Cinemática”
Capítulo 6: Efectos de Escala y Similitud Hidrológica
6.6
dy
i
=
dx
α m y m−1
(6.2)
y: tirante del flujo, x: distancia desde la cabecera del plano hacia aguas abajo, α y m: coeficientes
cinemáticos del plano, i: intensidad de lluvia en exceso.
Para flujo permanente no uniforme, con una condición de borde aguas arriba de tirante nulo,
integrando (6.2) se obtiene la expresión del tirante en función de la distancia recorrida:
⎛i x⎞
y (x ) = ⎜
⎟
⎝ α ⎠
1m
(6.3)
Integrando (6.3) para la longitud del plano, se obtiene (Goodrich, 1990):
L
1m
⎛ ix ⎞
Seq = ∫ ⎜ ⎟
0 ⎝α⎠
1m
dx =
m ⎛i⎞
⎜ ⎟
m +1 ⎝ α ⎠
L(m +1) m
(6.4)
S eq : almacenamiento de equilibrio por unidad de ancho del plano, L: longitud del plano.
S eq se puede expresar como tirante medio del flujo, dividiendo (6.4) por L. Como α depende de S
y N, S eq contempla tanto las características del plano (L, S y N) como de la lluvia (i).
El S eq de una subcuenca a agregar (ED) se calcula como la suma del volumen aportado por cada
uno de los segmentos que la componen (planos, cunetas, canales y conductos) (fuente: del autor a
los fines de esta investigación). Para ello, cada segmento se divide en subtramos por medio de n
secciones transversales y se calcula el área mojada en cada sección con la ecuación:
A = α ′ Q m′
⎛ 1⎞
α′ = ⎜ ⎟
⎝α⎠
m′ =
(6.5)
1m
(6.6)
1
m
(6.7)
α y m se calculan según el tipo de segmento (Anexo I), Q: caudal para la condición de equilibrio completo.
El almacenamiento de agua en cada segmento k, S k se calcula:
n −1
Sk = ∑ (A i + A i+1 )
i =1
∆x
2
(6.8)
i: sección transversal genérica, n: cantidad de secciones del segmento k, ∆x : incremento de longitud entre
dos secciones consecutivas.
Ing. Raúl A. Pedraza
Tesis Doctoral: “Efectos de Escala sobre la Simulación del Flujo de Agua Superficial
en Áreas Urbanas Usando Modelos Basados en la Onda Cinemática”
Capítulo 6: Efectos de Escala y Similitud Hidrológica
6.7
El almacenamiento total S eq del sector de cuenca a agregar se calcula como:
j
Seq = ∑ Sk
(6.9)
k =1
k: segmento genérico, j: cantidad de segmentos que componen el sector de cuenca analizado.
Las ecuaciones (6.5) a (6.9) fueron incorporadas al modelo OCRED-1 para el cálculo de los
almacenamientos en cada segmento y en cada intervalo de tiempo.
A continuación se ejemplifica numéricamente el efecto de escala sobre S eq .
Ejemplo Nº 6.2 (fuente: del autor a los fines de esta investigación).
Se calcularon con el modelo los almacenamientos de equilibrio para los esquemas descritos en el
Ejemplo Nº 6.1. Para ello, se consideró una lluvia en exceso de intensidad constante igual a
60mm/h y de 30 min de duración, suficientemente larga para alcanzar el equilibrio completo. Los
resultados se muestran en la Tabla Nº 6.2.
Tabla Nº 6.2: Almacenamientos de los esquemas (fuente: del autor, a los fines de esta
investigación).
Parámetro/
Variación
Sp
S cc
S eq
[m3]
A
B
C
19.3
44.3
19.3
3
7.3
0.0
0.0
3
26.6
44.3
19.3
3
-------
17.7
66.5
-7.3
-27.4
[m ]
[m ]
∆S eq [m ]
[%]
S p , S cc y S eq : almacenamientos de equilibrio aportados por los planos, cunetas y total, ∆S eq : variación
de S eq de una EA (B ó C) respecto de ED (A).
Para el esquema B, el efecto resultante es un aumento de S eq (EAN = ∆S eq = 17.7 m3), que se
corresponde con el aumento de t e visto en el Ejemplo Nº 6.1 (EAN = ∆t e = 5.4 min).
Para el esquema C, el efecto neto es una disminución de S eq (EAN = ∆S eq = - 7.3 m3), que se
corresponde con una reducción de t e (EAN = ∆t e = - 2.6 min).
6.2.2.
Relación entre el Almacenamiento y el Tiempo de Equilibrio de un Plano
En parcelas con infiltración, el cálculo analítico de t p se torna complejo y el cálculo numérico
introduce una incertidumbre, debido a la aproximación asintótica de estos procedimientos. Para
evitar esta incertidumbre, Overton (1971) propuso estimar t p en función del tiempo de retardo,
expresando éste en función de S eq .
Ing. Raúl A. Pedraza
Tesis Doctoral: “Efectos de Escala sobre la Simulación del Flujo de Agua Superficial
en Áreas Urbanas Usando Modelos Basados en la Onda Cinemática”
Capítulo 6: Efectos de Escala y Similitud Hidrológica
6.8
En la Figura Nº 6.3 se muestran superpuestos, un hietograma de intensidad de lluvia en exceso,
i(t) y el hidrograma q(t) correspondiente a la salida de un plano, expresados en las mismas
unidades de intensidad.
Figura Nº 6.3: Determinación del tiempo de equilibrio como función del tiempo de retardo (Overton,
1971).
El tiempo de retardo, t L , se define como la diferencia entre los centros de gravedad (momentos de
primer orden) del hidrograma de escurrimiento, M1Q y del hietograma de lluvia en exceso, M1P.
Como la intensidad es constante, el centroide del hietograma ocurre al tiempo medio de la
duración de la lluvia, t r .
Por otra parte, el volumen de lluvia en exceso es igual al volumen del hidrograma. Por lo tanto, la
mitad del volumen de lluvia en exceso (I + II) es igual a la mitad del volumen de escurrimiento (II +
III):
I + II = II + III
(6.10)
I = III
(6.11)
De donde:
Si en (6.11) se suma miembro a miembro el área de la “cuña” encerrada entre el hietograma y el
hidrograma y entre los tiempos M1P y el tiempo de equilibrio, se obtiene:
S eq
Ap
= i tL
(6.12)
S eq : almacenamiento de equilibrio, A p : área del plano, i: intensidad de lluvia en exceso, t L : tiempo de
retardo bajo la hipótesis de intensidad de lluvia constante.
El primer miembro expresa el almacenamiento de equilibrio en unidades de lámina (tirante medio
sobre el plano para la condición de equilibrio). Es el agua de detención superficial y representa el
área encerrada entre el hietograma y el hidrograma, desde t = 0 hasta el tiempo de equilibrio.
Ing. Raúl A. Pedraza
Tesis Doctoral: “Efectos de Escala sobre la Simulación del Flujo de Agua Superficial
en Áreas Urbanas Usando Modelos Basados en la Onda Cinemática”
Capítulo 6: Efectos de Escala y Similitud Hidrológica
6.9
Por lo tanto:
tL =
S eq
Ap
(6.13)
i
Dividiendo (6.4) miembro a miembro por (L i) y reemplazando en (6.13), se obtiene:
m ⎛⎜ L ⎞⎟
tL =
m + 1 ⎜⎝ α im − 1 ⎟⎠
1m
(6.14)
Reemplazando (5.49) en (6.14):
tp =
m+1
tL
m
(6.15)
m: coeficiente cinemático.
Una característica importante de (6.15) es que la relación entre t p y t L es independiente de la
intensidad de lluvia.
Reemplazando (6.13) en (6.15), se obtiene la relación entre S eq y t p :
tp =
m + 1 S eq A
m
i
(6.16)
Si en esta ecuación se ingresa el valor de S eq obtenido para la subcuenca a agregar (ED), el t p
obtenido para el PE (EA) se aproxima al t e de la subcuenca y se mantiene una similitud
hidrológica entre ambas escalas.
Para un plano con flujo turbulento, reemplazando (5.21) en (6.15), Overton (1971) obtuvo la
expresión:
t p = 1.6 t L
(6.17)
Esta ecuación fue utilizada por investigadores posteriores para determinar el tiempo de equilibrio
de parcelas de ensayo (Engman, 1986).
Se presenta a continuación un ejemplo de evaluación de t L y t p en función de S eq .
Ejemplo Nº 6.3 (fuente: del autor a los fines de esta investigación).
Se calcularon los valores de t L y t p con (6.13) y (6.15), respectivamente, para los esquemas
agregados del Ejemplo Nº 6.1. En la Tabla Nº 6.3.a se muestran los resultados obtenidos en base
a los valores de S eq previos al escalamiento y en la Tabla Nº 6.3.b, los valores calculados
manteniendo constante el S eq obtenido para el esquema A (ED).
Ing. Raúl A. Pedraza
Tesis Doctoral: “Efectos de Escala sobre la Simulación del Flujo de Agua Superficial
en Áreas Urbanas Usando Modelos Basados en la Onda Cinemática”
Capítulo 6: Efectos de Escala y Similitud Hidrológica
6.10
Tabla Nº 6.3.a: Tiempos de retardo y de equilibrio antes del escalamiento. (fuente: del autor, a los
fines de esta investigación).
Parámetro
B
C
m
1.667
1.667
S eq [m3]
44.3
19.3
t L [min]
8.9
3.4
t p [min]
14.2
6.2
Tabla Nº 6.3.b: Tiempos de retardo y de equilibrio después del escalamiento (fuente: del autor, a
los fines de esta investigación).
Parámetro
B
C
m
1.667
1.667
S eq [m3]
26.6
26.6
t L [min]
5.3
5.3
t p [min]
8.5
8.5
En la Tabla Nº 6.3.a, los valores de t p obtenidos en base a los almacenamientos S eq calculados
con el modelo son idénticos a los de la Tabla Nº 6.1, determinados con (5.50).
En la Tabla Nº 6.3.b puede observarse que los valores de t p obtenidos aproximan aceptablemente
el t e de ED (8.8 min), con un error relativo de -3%. Se verifica que conservando S eq se mantiene
t e y, en consecuencia, una similitud hidrológica entre las escalas.
6.2.3.
Rugosidad Efectiva
La rugosidad efectiva o computacional del PE (EA), que reemplaza una subcuenca compleja a
agregar (ED), se expresa (Goodrich, 1990):
*
N =
S ⎛ m + 1⎞
⎜
⎟
i ⎝ m ⎠
m
⎛ S eq ⎞
⎜
⎟
⎜ W ⎟
⎝
⎠
m
⎛ 1⎞
⎜ ⎟
⎝L⎠
m+1
(6.18)
N* : rugosidad efectiva del PE (EA), W, L y S: ancho, longitud y pendiente del PE.
La ecuación (6.18) se obtiene sustituyendo α por (5.20) en (6.4) (se asume la hipótesis de flujo
turbulento).
La rugosidad efectiva se simboliza con N* para diferenciarla de la rugosidad de ED, N, ya que
deja de tener el mismo significado físico que ésta. Mientras N es un parámetro hidráulico de los
planos de ED, N* es un parámetro computacional del PE que permite conservar S eq , de modo
que las respuestas hidrológicas del modelo con EA y ED sean similares (anula EAN).
Ing. Raúl A. Pedraza
Tesis Doctoral: “Efectos de Escala sobre la Simulación del Flujo de Agua Superficial
en Áreas Urbanas Usando Modelos Basados en la Onda Cinemática”
Capítulo 6: Efectos de Escala y Similitud Hidrológica
6.11
Si se aplican las ecuaciones (6.13) y (6.17) al PE, se obtiene el mismo valor de t p que con (5.50),
considerando en ésta N* .
Ejemplo Nº 6.4 (fuente: del autor a los fines de esta investigación).
A partir de (6.18) se calcularon los valores de N* para los esquemas agregados (B y C) del
Ejemplo Nº 6.1, de manera de mantener constante el S eq obtenido para el esquema A (26.6 m3).
Los valores obtenidos se muestran en la Tabla Nº 6.4.
Tabla Nº 6.4: Valores de N (escala A) y N* (escalas B y C) (fuente: del autor, a los fines de esta
investigación).
Parámetro/
Variación
N ó N*
∆N* [%]
A
B
C
0.050
-------
0.021
0.085
-57.3
70.8
N: rugosidad de ED (A), N* : rugosidad efectiva del PE de EA (B ó C), ∆N * : variación de N* respecto de
N.
Con el esquema B, para mantener constante S eq se debe aplicar una rugosidad efectiva N* =
0.021, menor que la rugosidad de ED (N = 0.050). Con el esquema C, para conservar S eq se
debe aplicar N* = 0.085, mayor que N. Como puede observarse, para mantener constante S eq se
debe utilizar una rugosidad efectiva para cada EA.
Se realizaron corridas con el modelo aplicando los valores de N* obtenidos para las EA. Se
consideraron dos duraciones de lluvia, 5 min y 10 min, menor y mayor al t p de los planos de EA
(8.5 min), respectivamente. Los resultados se muestran en la Figura Nº 6.4.
Para la duración t r = 10 min, los planos de EA (B y C) alcanzan un equilibrio cinemático completo
y el hidrograma simulado con la EA mantiene una similitud con el hidrograma obtenido con ED.
En cambio, para la duración t r = 5 min, los planos de EA (B y C) alcanzan un equilibrio parcial y el
hidrograma simulado con la EA incorpora un error por defecto en el caudal pico, aún cuando se
aplica N* . Este error se debe a que el caudal a la salida del plano de EA no alcanza el valor dado
por (5.57), sino uno menor dado por (5.59). En consecuencia, no se conserva el S eq .
Para evaluar este error bajo condiciones reales de cuencas con infiltración, se simularon con el
modelo los hidrogramas para los esquemas A, B y C, considerando que la cuenca tiene una
superficie impermeable directamente conectada del 40% (valor representativo de una urbanización
media) y una superficie permeable con un valor del parámetro CN = 80 (método del Número de
Curva, U. S. Soil Conservation Service, 1986). En la figura se muestran los hidrogramas obtenidos
(“INF”).
Ing. Raúl A. Pedraza
Tesis Doctoral: “Efectos de Escala sobre la Simulación del Flujo de Agua Superficial
en Áreas Urbanas Usando Modelos Basados en la Onda Cinemática”
Capítulo 6: Efectos de Escala y Similitud Hidrológica
6.12
Se observa que en el caso de cuencas con infiltración, el error absoluto que introduce el equilibrio
parcial en los caudales pico simulados con EA (0.004 m3/s) es menor que el error bajo la hipótesis
de superficie impermeable (0.017 m3/s): el error es mitigado por las pérdidas de escurrimiento.
Figura Nº 6.4: Hidrogramas simulados luego del escalamiento (fuente: del autor, a los fines de
esta investigación).
0.090
0.080
CAUDAL [m3/s]
0.070
0.060
0.050
0.040
0.030
0.020
0.010
0.000
0
5
10
ESCALA A (N = 0.050) - tr = 5 min
ESCALA B (N* = 0.021) - tr = 5 min
ESCALA C (N* = 0.085) - tr = 5 min
ESCALA A (N = 0.050) - tr = 5 min, INF
ESCALA C (N* = 0.085) - tr = 5 min, INF
15
20
25
TIEMPO
30[min]
ESCALA A (N = 0.050) - tr = 10 min
ESCALA B (N* = 0.021) - tr = 10 min
ESCALA C (N* = 0.085) - tr = 10 min
ESCALA B (N* = 0.021) - tr = 5 min, INF
Sintetizando, para conservar una similitud hidrológica entre ED y EA, se debe mantener el S eq
entre ambas escalas. Para ello, se debe aplicar una rugosidad efectiva al plano equivalente de
EA y éste debe alcanzar un equilibrio cinemático completo con el evento en estudio.
Ing. Raúl A. Pedraza
Tesis Doctoral: “Efectos de Escala sobre la Simulación del Flujo de Agua Superficial
en Áreas Urbanas Usando Modelos Basados en la Onda Cinemática”
Capítulo 6: Efectos de Escala y Similitud Hidrológica
6.13
A partir de los conceptos y desarrollos presentados, se elaboraron las siguientes conclusiones
para este Capítulo:
a)
La agregación de un esquema de ED implica que una subcuenca, compuesta por un conjunto
segmentos (planos, cunetas y eventualmente, canales y conductos), sea reemplazada por un
único PE (EA). La agregación tiene dos componentes: geométrico y de procesos.
b)
La agregación geométrica consiste en la modificación de la longitud típica de los planos. Su
efecto sobre la respuesta hidrológica (EAG) atrasa el pico (si L EA > L ED ) o es nulo (si
L EA = L ED ).
c)
La agregación de procesos consiste en la remoción de cordones cuneta, canales y
conductos de menor jerarquía con el aumento de escala. Produce una pérdida de
almacenamiento en la red de drenaje, por lo que su efecto (EAP) anticipa el pico del
hidrograma.
d)
Los efectos individuales (EAG y EAP) actúan simultáneamente sobre el hidrograma simulado
con EA. Si predomina alguno de éstos, el efecto de agregación neto (EAN) modifica la
respuesta hidrológica.
e)
Para mantener una similitud hidrológica entre escalas, es necesario conservar t e . Esto
equivale a anular EAN. Para ello, se debe recurrir al escalamiento de los parámetros.
f)
Los efectos de la agregación sobre los resultados de la simulación del flujo de agua
superficial se manifiestan en: i) errores en el tiempo al pico, si el plano de EA alcanza un
equilibrio cinemático completo e ii) errores en el tiempo al pico y en el caudal pico, si dicho
plano alcanza un equilibrio parcial.
g)
El almacenamiento de equilibrio, S eq , es una poderosa medida de la función de respuesta de
una cuenca, ya que integra los efectos de la topografía, convergencia del flujo y rugosidad
hidráulica.
h)
Si se conserva S eq entre ED y EA, se conserva t e y por lo tanto, una similitud hidrológica
entre ambas escalas.
i)
La rugosidad efectiva del PE, N* , es un parámetro que permite conservar S eq y por lo tanto,
una similitud hidrológica entre EA y ED. Es un parámetro computacional obtenido del
escalamiento y deja de tener el mismo significado físico que la rugosidad de ED, N.
j)
Para mantener constante S eq se debe aplicar una rugosidad efectiva al plano de EA y éste
debe alcanzar un equilibrio cinemático completo.
k)
Si un plano de EA alcanza un equilibrio parcial, el hidrograma simulado con la EA incorpora un
error por defecto en el caudal pico, aún cuando se aplique N* . Este error puede ser mitigado
si existen pérdidas de escurrimiento en la cuenca.
Ing. Raúl A. Pedraza