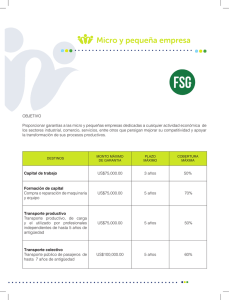
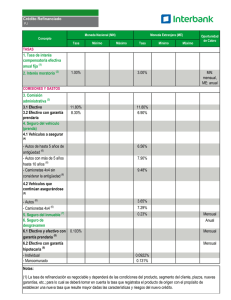
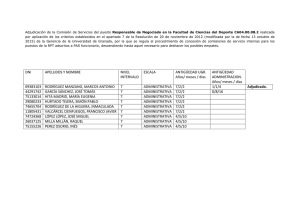
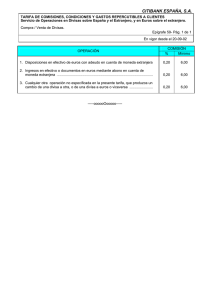
0 0 3 0 3 ( ) 3 3 6 0 6 si x x x si x f x x si x si x

MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II
BLOQUE 1
A) 1) Despeja la matriz X en la ecuación: XAB − XC = 2C
1 2
 2 −1 
 0 1
; B = 
; C = 

0 3
1 2 
 −1 2 
2) Halla X siendo las matrices: A = 
B) Sumando los años de antigüedad de tres empleados A, B y C se obtienen 50 años. El doble
de la suma de las antigüedades de B y de C es igual al triple de la antigüedad de A. La
diferencia de antigüedad entre B y C es el 30% de la antigüedad de A Determinar los años de
antigüedad de cada empleado.
BLOQUE 2
A) Una fábrica de avionetas va a lanzar al mercado dos nuevos modelos (uno básico y otro de
lujo). El coste de fabricación del modelo básico es de 1 millón de euros, y el del modelo de lujo
1,5 millones de euros; disponiendo para esta operación de lanzamiento de 60 millones de euros.
Para evitar riesgos, de momento se cree conveniente lanzar al menos tantas avionetas del
modelo básico como del modelo de lujo y, en todo caso, no fabricar más de 45 avionetas del
básico. 1)¿Cuántas avionetas puede fabricar de cada modelo? Plantear el problema y representar
la región factible. 2) ¿Cuántas le interesan si su objetivo es maximizar el número total de
avionetas fabricadas? ¿Agota el presupuesto disponible?
B) Ana, Juan y Raúl, que están esperando para una consulta médica, sortean el orden en el que
van a entrar. 1) Calcula la probabilidad de que los dos últimos en entrar sean hombres.
2)Determina si son independientes los sucesos; A: ”la mujer entra antes que alguno de los
hombres”, B: “los dos hombres entran consecutivamente”.
BLOQUE 3
0 si x < 0

2
3 x − x si 0 < x < 3
A) Sea la función: f ( x) = 
1) Represéntala gráficamente. 2) Estudia
 x − 3 si 3 < x ≤ 6
0 si x > 6
su continuidad. 3) Calcula el área de la región limitada por el eje OX y la función.
B) Un agricultor dispone de 54.000 kg de fruta que puede vender a 0´2 €/kg. Cada día que pasa,
el precio aumenta 0´025 €, pero se estropean 1.000 kg. 1) Calcular cuándo le interesa vender la
fruta para obtener los máximos ingresos posibles. 2) ¿A cuánto ascenderán esos ingresos?
BLOQUE 4
A) Tenemos tres cajas, una verde, una roja y una amarilla y, en cada caja hay una moneda. La
de la caja verde está trucada y la probabilidad de que salga cara es doble de la probabilidad de
que salga cruz; la moneda de la caja roja tiene dos caras y la de la caja amarilla no está trucada.
Se toma una caja al azar y se lanza la moneda que está en la caja. Calcula: 1) La probabilidad de
que no salga cara 2) La probabilidad de que sabiendo que ha salido cara, se haya lanzado la
moneda de la caja roja.
B) La distribución de la longitud de la cola del colirrojo tizón se considera normal. Hemos
capturado 81 individuos y se ha obtenido una media de 6´4 cm. y una desviación típica de 3.
Encontrar un intervalo de confianza al 98´4% para la media de la longitud de la cola. Interpretar
el valor obtenido.