1.- La figura describe la posición de un cuerpo en
Anuncio
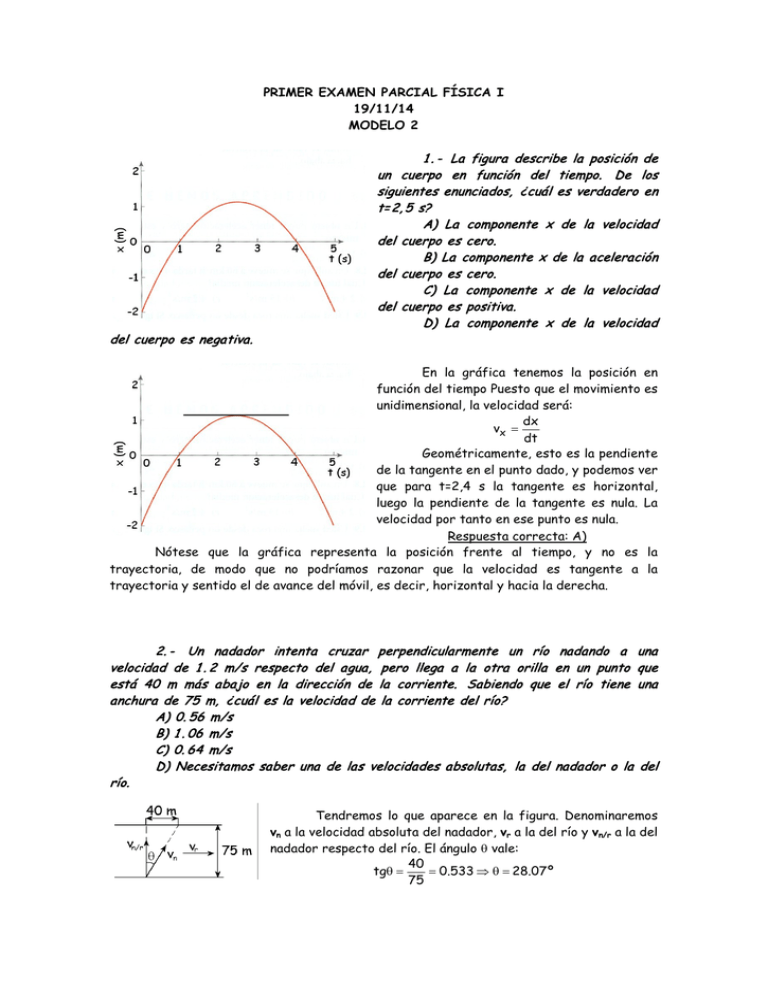
PRIMER EXAMEN PARCIAL FÍSICA I 19/11/14 MODELO 2 del cuerpo es negativa. 1 . - La figura describe la posición de un cuerpo en función del tiempo. De los siguientes enunciados, ¿cuál es verdadero en t=2, 5 s? A) La componente x de la velocidad del cuerpo es cero. B) La componente x de la aceleración del cuerpo es cero. C) La componente x de la velocidad del cuerpo es positiva. D) La componente x de la velocidad En la gráfica tenemos la posición en función del tiempo Puesto que el movimiento es unidimensional, la velocidad será: dx vx = dt Geométricamente, esto es la pendiente de la tangente en el punto dado, y podemos ver que para t=2,4 s la tangente es horizontal, luego la pendiente de la tangente es nula. La velocidad por tanto en ese punto es nula. Respuesta correcta: A) Nótese que la gráfica representa la posición frente al tiempo, y no es la trayectoria, de modo que no podríamos razonar que la velocidad es tangente a la trayectoria y sentido el de avance del móvil, es decir, horizontal y hacia la derecha. 2. - Un nadador intenta cruzar perpendicularmente un río velocidad de 1 . 2 m/s respecto del agua, pero llega a la otra orilla está 40 m más abajo en la dirección de la corriente. Sabiendo que anchura de 75 m, ¿cuál es la velocidad de la corriente del río? A) 0. 56 m/s B) 1 . 06 m/s C) 0. 64 m/s D) Necesitamos saber una de las velocidades absolutas, la del río. nadando a una en un punto que el río tiene una nadador o la del Tendremos lo que aparece en la figura. Denominaremos vn a la velocidad absoluta del nadador, vr a la del río y vn/r a la del nadador respecto del río. El ángulo θ vale: 40 tgθ = = 0.533 ⇒ θ = 28.07 º 75 Tomando unos ejes cartesianos normales (X horizontal y positivo hacia la derecha, e Y vertical y positivo hacia arriba tendremos: vn/r=vn-vr ⇒ vn/rj=vnsenθi+vncosθj-vri ⇒ 1.2j=vnsen28.07ºi+vncos28.07ºj-vri Igualando componentes en el eje Y: 1.2=vncos28.07º ⇒ vn=1.36 m/s E igualando componentes en el eje X: 0=vnsen28.07º-vr ⇒ vr=vnsen28.07º=1.36sen28.07º=0.64 m/s Respuesta correcta: C) 3. - En un ascensor se coloca una báscula, sobre la cual nos pesamos. El ascensor sube con aceleración constante. ¿Qué marca la báscula? A) Nada. B) Un peso mayor que el que tenemos. C) Un peso menor que el que tenemos. D) Nuestro peso. La báscula mide siempre la reacción normal. Si hacemos nuestro diagrama de sólido libre tendremos lo que aparece en la figura. Aplicando la segunda ley de Newton tendremos: ΣFY=maY ⇒ N-mg=ma ⇒ N=mg+ma Luego vemos que la bascula marca más de lo que pesamos. Respuesta correcta: B) 4.- Dos bloques A y B, de 1 kg y 2 kg de masa respectivamente, están apoyados sobre una superficie horizontal sin rozamiento. Sobre ellos actúa una fuerza horizontal de 6 N. La fuerza que el bloque B ejerce sobre el bloque A es: A) 0 B) 6 N C) 3 N D) 4 N Los dos bloques se mueven con la misma aceleración. Si hacemos el diagrama de sólido libre de los dos bloques tendremos lo que se muestra en la figura. Aplicando la segunda ley de Newton: ΣFX=(mA+mB)aX ⇒ F=(mA+mB)a 6=(1+2)a ⇒ a=2 m/s2 Ahora hacemos el diagrama de sólido libre del cuerpo A y tendremos: ΣFX=mAaAX ⇒ F-N=mAa ⇒ 6-N=1 · 2 ⇒ N=4 N Respuesta correcta: D) También podríamos haber hecho el diagrama de sólido libre del cuerpo B. Para ello, hay que tener en cuenta la ley de acción-reacción (tercera ley de Newton), que dice que la reacción que ejerce B sobre A es igual y de sentido contrario a la que ejerce A sobre B. Así, tendríamos con este bloque: ΣFX=mBaBX ⇒ N=mBa=2 · 2=4 N Vemos que se obtiene exactamente el mismo resultado. 5. - Un bloque de 2 kg está sobre un plano inclinado 30º respecto a la horizontal. El coeficiente de rozamiento estático entre el bloque y el plano es de 0, 6 y el dinámico 0, 5. Determina la aceleración del bloque. A) Nula B) 4, 9 m/s2 C) 0, 656 m/s2 D) 0, 1 92 m/s2 Hacemos el diagrama de sólido libre del bloque, y miramos primero si hay movimiento o si el rozamiento es suficiente para impedir el deslizamiento. Si el equilibrio es posible tendremos: ΣFX=0 ⇒mgsen30º-Fr=0 ⇒ Fr=mgsen30º ΣFY=0 ⇒ N-mgcos30º=0 ⇒ N=mgcos30º Si no hay deslizamiento se deberá cumplir que: Fr≤µN ⇒ mgsen30º≤µmgcos30º ⇒ sen30º≤µcos30º ⇒ sen30º≤0,6cos30º ⇒ 0,5≤0,52 Vemos que esto es cierto, luego no hay movimiento, la aceleración es nula. Respuesta correcta: A) 6. - Una fuerza conservativa paralela al eje X actúa sobre una partícula que se mueve sobre el eje X. La fuerza produce una energía potencial dada por x3 x2 + − 1 2 x + 6 en unidades del SI. Determina los puntos de equilibrio 3 2 y el tipo de equilibrio en ellos. A) x=3 m equilibrio estable, x=- 4 m equilibrio inestable B) x=3 m equilibrio inestable, x=- 4 m equilibrio estable C) x=- 3 m equilibrio estable, x=4 m equilibrio inestable D) x=- 3 m equilibrio inestable, x=4 m equilibrio estable U( x ) = Puesto que la fuerza es conservativa tendremos que: dU F=− dx Por tanto, si queremos encontrar los puntos de equilibrio tendremos que en ellos la fuerza neta aplicada es nula: dU − 1 ± 12 + 4 ⋅ 1 ⋅ 12 3 m = 0 ⇒ −x2 − x + 12 = 0 ⇒ x2 + x − 12 = 0 ⇒ x = = dx 2 ⋅1 − 4 m Para saber el tipo de equilibrio tenemos que ver si nos encontramos en un máximo o mínimo de la curva de potencial, para lo cual tenemos que ver el signo de la segunda derivada del potencial. Tendremos: F=− U(x) = x 3 x2 + − 12x + 6 ⇒ U'(x) = x2 + x − 12 ⇒ U''(x) = 2x + 1 3 2 Así, tendremos: x=3 m ⇒ U’’(3)=2x+1=2 · 3+1=7>0 ⇒ Mínimo de la curva ⇒ Equilibrio estable x=-4 m ⇒ U’’(-4)=2x+1=2 · (-4)+1=-7<0 ⇒ Máximo de la curva ⇒ Equilibrio inestable Respuesta correcta: A) 7. - Dos objetos de masas m1 y m2 respectivamente son liberados desde el reposo y desde la misma altura como indica la figura. Deslizan sin fricción hasta llegar al tramo horizontal que es rugoso. Sabiendo que el coeficiente de fricción es el mismo para ambas masas. ¿Cuál de las siguientes afirmaciones es cierta? A) Ambos objetos tiene inicialmente la misma energía potencial gravitatoria. B) Ambos objetos tienen la misma energía cinética cuando llegan al inicio del tramo rugoso. C) Ambos objetos recorren la misma distancia antes de parar. D) El objeto de mayor masa recorre menos distancia antes de parar. Aplicamos el teorema de conservación de la energía. Tomamos como nivel de energía potencial nula la más baja, es decir, el nivel del tramo rugoso. Aplicamos por tanto la conservación de la energía entre la posición inicial, en que toda le energía es potencial gravitatoria, y la posición final, en que la energía total es nula puesto que no hay ni potencial gravitatoria (la altura es nula) ni cinética (el bloque se detiene). Tendremos pues: ETinicial+WFuerzas=ETfinal ⇒ EPg+WFuerzas=0 Aparte de la fuerza de atracción gravitatoria, sobre el cuerpo actúan la normal y en el tramo rugoso la fuerza de rozamiento. La normal no realiza trabajo porque en todo momento es perpendicular al desplazamiento. Por tanto tendremos que la única fuerza que realiza trabajo es la fuerza de rozamiento: EPg+WFuerzas=0 ⇒ mgh+Fr · d=0 siendo d la distancia que el bloque recorre por el plano horizontal rugoso. Del diagrama de sólido libre puesto que el bloque no se mueve en la dirección vertical: ΣFy=0 ⇒ N-mg=0 ⇒ N=mg Y como el bloque desliza, la fuerza de rozamiento adquiere su valor máximo: Fr=(Fr)máx=µN=µmg h mgh+Fr · d=0 ⇒ mgh+µNdcos180º=0 ⇒ mgh-µmgd=0 ⇒ d = µ Vemos que la distancia que recorre el bloque en la horizontal es independiente de la masa, luego ambos objetos recorren la misma distancia antes de parar. Respuesta correcta: C) 8. - Defina el momento angular de una partícula. Demostrar su relación con el momento de las fuerzas. Demostrar que si las fuerzas que se ejercen sobre la partícula son centrales, el movimiento es plano. Se define el momento angular (respecto de un cierto punto O) como el momento de la cantidad de movimiento (mv) con respecto a dicho punto O: LO=r x mv Tomando derivadas: LO = r × mv ⇒ dLO dr dp dp = × mv + r × = r× = r × F = MO dt dt dt dt dLO = MO dt (esta ecuación sólo es correcta si L y M se evalúan respecto del mismo punto O). De esta expresión se deriva el siguiente principio de conservación: “si la resultante de los momentos de las fuerzas es nula, el momento angular permanece cte.” En el caso de fuerzas centrales la fuerza F es siempre paralela (está dirigida) a la dirección de r:, por lo que el momento de la fuerza es nula. Mo ≡ 0 ⇒ L0 ≡ cte Como LO=r x mv, L será un vector perpendicular al plano formado por r y v. De esta forma, si L debe ser constante, siempre deberá tener la misma dirección, es decir perpendicular al plano formado por r y v, luego la partícula deberá moverse en un plano.








