LAB 7
Anuncio
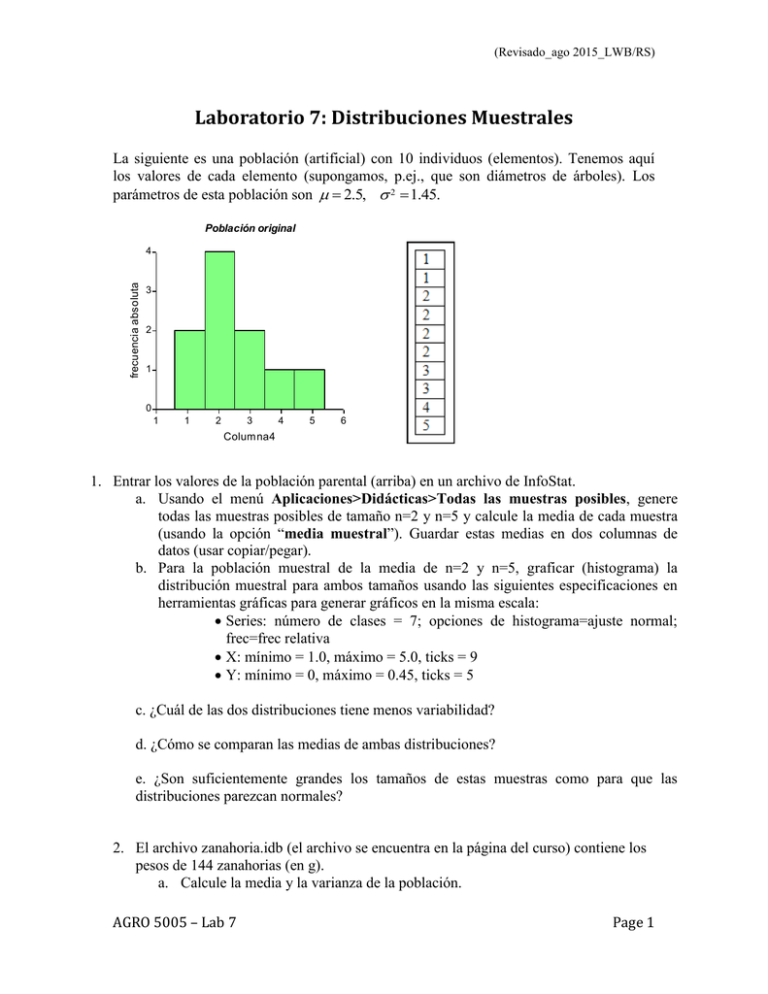
(Revisado_ago 2015_LWB/RS) Laboratorio 7: Distribuciones Muestrales La siguiente es una población (artificial) con 10 individuos (elementos). Tenemos aquí los valores de cada elemento (supongamos, p.ej., que son diámetros de árboles). Los parámetros de esta población son 2.5, 2 1.45. Población original frecuencia absoluta 4 3 2 1 0 1 1 2 3 4 5 6 Columna4 1. Entrar los valores de la población parental (arriba) en un archivo de InfoStat. a. Usando el menú Aplicaciones>Didácticas>Todas las muestras posibles, genere todas las muestras posibles de tamaño n=2 y n=5 y calcule la media de cada muestra (usando la opción “media muestral”). Guardar estas medias en dos columnas de datos (usar copiar/pegar). b. Para la población muestral de la media de n=2 y n=5, graficar (histograma) la distribución muestral para ambos tamaños usando las siguientes especificaciones en herramientas gráficas para generar gráficos en la misma escala: Series: número de clases = 7; opciones de histograma=ajuste normal; frec=frec relativa X: mínimo = 1.0, máximo = 5.0, ticks = 9 Y: mínimo = 0, máximo = 0.45, ticks = 5 c. ¿Cuál de las dos distribuciones tiene menos variabilidad? d. ¿Cómo se comparan las medias de ambas distribuciones? e. ¿Son suficientemente grandes los tamaños de estas muestras como para que las distribuciones parezcan normales? 2. El archivo zanahoria.idb (el archivo se encuentra en la página del curso) contiene los pesos de 144 zanahorias (en g). a. Calcule la media y la varianza de la población. AGRO 5005 – Lab 7 Page 1 (Revisado_ago 2015_LWB/RS) b. Prepare un histograma de frecuencias relativas con las observaciones en esta población (use para el eje Y un mínimo de 0/máximo de 0.40, con ticks = 5 y decimales = 0; X de 0 a 1200 con ticks = 9 y decimales = 0). 3. Para verificar las propiedades de la distribución muestral de la media, vamos a tomar muestras con reemplazo de la población de zanahorias descripta en la parte 2. Use el menú Aplicaciones>Didácticas>Remuestreo. Luego, seleccione la opción de “Aleatorio con reposición”. a. Escoja 1000 muestras con reposición de tamaño n=4 y use la opción de guardar la media muestral. b. Calcule la media y la varianza poblacionales de la población de 1000 medias de tamaño n=4. c. Prepare un histograma de frecuencias relativas de la población de 1000 medias de tamaño 4. (9 clases; Y de 0 a 0.40 con ticks = 5 y decimales = 0; X de 0 a 1200 con ticks = 9 y decimales = 0) d. Repita las partes a, b y c para tamaño de muestra n=16. e. Comparar las medidas de resumen de la población original, de la población de medias de n=4, y de la población de medias de n=16. f. Comparar los histogramas de la población original, de la población de medias de n=4, y de la población de medias de n=16. 4. La distribución del porcentaje de grasa láctea en ganado Holstein durante la década de 1970 era aproximadamente normal con una media de 3.4 y una desviación estándar de 0.3. (a) ¿Qué porcentaje de las vacas producían leche con menos de 3% de grasa? (b) ¿Qué porcentaje de las vacas producían leche con más de 4% de grasa? (c) Calcule el percentil 95 de la distribución de grasa láctea. Interprete este valor. AGRO 5005 – Lab 7 Page 2 (Revisado_ago 2015_LWB/RS) 5. Supongamos que una muestra aleatoria de n 25 vacas Holstein se selecciona de la población mencionada en el problema 4. A cada vaca se le mide el porcentaje de grasa en su leche, y se calcula la media muestral. (a) ¿Cómo sería la distribución de los valores posibles de Y ? (b) Compare la forma de la distribución de Y con la forma de la distribución de Y (el porcentaje de grasa láctea en cada vaca). Calcule la probabilidad que una muestra aleatoria de tamaño 25 tenga una media muestral menor de 3. (ayuda: 𝑧 = (𝑌̅ – 𝑌̅)/(𝑌̅ Compare este resultado con el de 4a. AGRO 5005 – Lab 7 Page 3