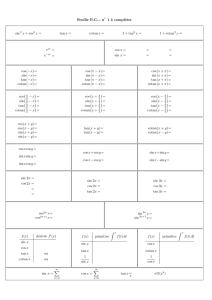
ملخص درس الدوال الأصلية - E

‫ ة وا رض‬# ‫م ا‬
‫و‬%& ' ‫م‬
‫ھ‬12 ‫ي‬
‫ا‬
‫)ك‬%
‫ت‬
‫ ىا‬+ ‫ت‬
‫ذ ﻣ دة ا‬
‫ا‬
‫أ‬
‫ذ‬
‫ا‬:‫ز‬
‫و ا ي‬
‫ﻣ‬
‫ ا‬.‫ﻣ‬
:% 5 ‫ درس ا وال ا‬3 ‫ﻣ‬
f ( x) = −
(x
(x
2
2
− 1)′
− 1)
0
f ( x) = −
2
(5
x
( x −1)
2
*‫ا وال ا‬
2
k ∈ ℝ , - F ( x) = 1 + k ‫اذن‬
2
f ( x) =
x −1
1
f ( x ) = 2 2x + 1 = ( 2 x + 1)′ ( 2x + 1) 2 (6
k ∈ℝ, -
F ( x) =
1
1
+1
2
( 2x +1)
1
+1
2
+k
1
x
‫اذن‬
)
2x + 1 + k 70
3
(x
f ( x) =
3
(
x
2
− 1)
2
x
x +1
2
=
(x
2
+ 1)′
x2 + 1
:,
: ‫*ن‬
k ∈ℝ
‫دا‬
1
1
F ( x) = 5 × x5 + 3 × x2 + 1x + k ‫اذن‬
5
2
f ( x) =
(8
1
7
+cos x +sin x −1(2
‫اذن‬
k ∈ℝ
f ( x) = sin x + x cos x = x′sin x + x( sin x)′ (3
k ∈ ℝ , - F ( x) = x × sin x + k ‫اذن‬
0
f ( x ) = cos xe sin x = ( sin x )′ e sin x (9
I
f ‫ا‬
6 I‫ل‬
‫د‬
. - ‫دا‬
,
:‫ ن‬, I
f +g ‫ا‬
1
3
( 2 x − 1)′ ( 2 x − 1) (4
2
k ∈ ℝ , - F ( x) = 1 × 1 ( 2x −1)3+1 + k ‫اذن‬
2 3 +1
k ∈ ℝ , - F ( x) = 1 ( 2x −1)4 + k 70 ‫و‬
8
f ( x ) = ( 2 x − 1) =
3
F ( x ) = e sin x + k 70 ‫و‬
*‫ا وال ا‬
ℝ
y0 ‫و‬
I
x
F ( x ) = 2 x + sin x − cos x − x + k ‫اذن‬
x4 + 2 > 0
1
x 3 (8
x +2
4
f ( x) = 5x4 + 3x +1 (1: %) :‫أ‬
k ∈ ℝ , - F ( x) = x2 + 1 + k ‫اذن‬
k ∈ℝ
‫ دا‬f
:1 % 5 7
,I
‫ا‬
‫ دا أ‬F ‫و‬, I ‫ل‬
‫ ھ ا وال‬I
f ‫ا‬
*‫ا وال ا‬
, x ֏ F ( x) + k :
" I
‫ا‬
f ( x ) = cos xe sin x (9
2 x +1
′
4
x3
1 ( x + 2) 0
=
x4 + 2 4 x4 + 2
- F ( x ) = 1 ln x 4 + 2 + k :
4
1
F ( x ) = ln ( x 4 + 2 ) + k :
4
:8 92
I‫ل‬
, I
f ‫ا‬
‫دا أ‬
f $ % ‫و‬, I
‫ " ! ق‬# F ‫دا‬
( ∀x ∈ I ) ; F ′ ( x ) = f ( x ) ‫أي‬, ‫ھ‬
(7 f ( x ) = 2 2 x + 1 (6
I = ℝ; f ( x ) =
(7
kf
.
:% ‫د‬
F % 5 ‫ا وال ا‬
f %‫ا ا‬
− a sin ( ax + b )
cos ( ax + b )
a cos ( ax + b )
e
sin ( ax + b )
l n x +k
1
x
u ′ + v′
ln u ( x ) + k
u′ ( x )
1
x r +1 + k
r +1
eu + k
x r ; r ∈ ℚ∗ −{−1}
u ′ × v + u × v′
1
+k
u
u
+k
v
u′
u2
u ′ × v − u × v′
v2
u n ×u ′
1 n +1
u +k
n +1
f %‫ا ا‬
e +k
u ×v + k
−
F % 5 ‫ا وال ا‬
x
u +v + k
:‫ذ‬
‫ا‬
‫ دا‬f
‫د‬
‫و‬
2
f ( x) =
‫د‬
‫وال ا‬
(5 f ( x ) = ( 2 x − 1)3 (4
x
k ∈ℝ
f ( x) =
‫ ت‬5 7 ‫ و‬8 ‫ ر‬92 :% 5 ‫ا وال ا‬
:% ‫أﻣ‬
4
+cosx+sinx−1 (2 f ( x) =5x +3x+1(1
f ( x) =
k ∈ ℝ , - F ( x) = 2 ( 2x + 1) + k 70 ‫و‬
3
2
2
( 2x +1) 2 =
3
3
‫د‬:
f ( x) = sin x + x cos x (3
3
2
F ( x) =
1
x
. -‫ د‬k,‫د‬
‫ دا‬f
:2 % 5 7
I ‫ ا‬/0 x0 ‫ و‬I ‫ل‬
. 1
‫ دا أ‬5 6 ‫ دا‬f 2 ‫إذا‬
G ‫ ة‬-‫و‬
‫ دا أ‬916
G ( x0 ) = y0 :, :"
/ ‫ دا‬:3 % 5 7
.I
‫دا أ‬
‫ دا‬g ‫ و‬f
:4 % 5 7
k ‫و‬, I ‫ل‬
‫ دا أ‬G ‫ و‬F 2 ‫إذا‬
g‫ و‬f
‫ا‬
‫ا‬1 ‫ا‬
‫ دا أ‬F + G ‫ا ا‬
.I
‫ا‬
‫ دا أ‬kF ‫ا ا‬
‫ وال ا‬% 5‫ ول دوال أ‬:
F % 5 ‫ا وال ا‬
ax + k ; k ∈ ℝ
2
x
+ k
2
f %‫ا ا‬
a; ( a ∈ ℝ )
x
1 n+1
x +k
n +1
xn ; n ∈ ℕ∗ − {1}
u ′eu
1
+k
x
2 x +k
− cos x + k
sin x
sin x + k
1
x2
1
x
cos x
2 u +k
u′
u
tan x + k
(
u ( x)
)
−
1 + tan2 x =
1
cos2 x
http:// xyzmaths.e-monsite.com