File
Anuncio

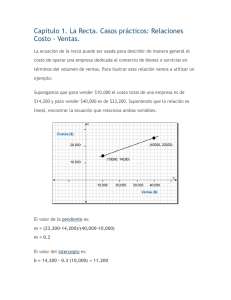
Universidad Nacional José María Arguedas Carrera Profesional de Administración de Empresas CONICAS – LA RECTA Lic. JOSÉ L. ESTRADA P. ANDAHUAYLAS – PERÚ Cónicas A. Introducción La introducción de la geometría analítica representa uno de los adelantos más importantes en el desarrollo de la matemática. El concepto de sistema coordenado, que caracteriza a la geometría analítica fue introducido por primera vez en 1637 por el matemático René Descartes (1590-1650). Por esta razón la geometría analítica se conoce también con el nombre de “Geometría Cartesiana Por medio de un sistema coordenado es posible obtener una correspondencia biunívoca entre puntos y números reales; esto es, nos permitirá aplicar los métodos del análisis a la geometría, y de ahí el nombre de geometría analítica. Así mismo, nos permitirá usar ventajosamente los métodos algebraicos en la solución de problemas geométricos. Dos son los problemas fundamentales de la geometría analítica: 1° Dada una ecuación interpretarla geométricamente. 2° Dada una figura geométrica, determinar su ecuación En efecto: CONSTRUCCIÓN DE CURVAS : La discusión de una curva y su representación gráfica constituye un problema de tan gran importancia en todas las ramas de la matemática y sus aplicaciones. Nosotros hemos considerado este problema parcialmente en la sección 2 del capítulo 6, donde nos dedicamos a curvas que son la gráfica de funciones reales de una variable real. Sugerimos al lector vuelva a leer la sección 6.2. El término cónicas hace referencia al hecho de la intersección del cono con planos. Las figuras 1 al 7 muestran las posibles maneras de intersectar un cono (doble) con un plano. Cónicas – La recta 2 Circunferencia Elipse Parábola Fig. 1 Fig. 2 Fig. 3 • Hipérbola Punto Recta Fig. 4 Fig. 5 Fig. 6 Dos rectas que se cortan Fig. 7 Las cuatro primeras se refiere a las cónicas básicas (cónicas no degeneradas): circunferencia, elipse, parábola e hipérbola; y las tres restantes señala a las cónicas degeneradas: punto, recta, y dos rectas que se cortan. Lic. José L. Estrada P. UNAJMA Cónicas – La recta 3 Hay varias formas de estudiar las cónicas: 1°. Podríamos empezar definiéndolas como lo hicieron los matemáticos griegos, en términos de conos con planos, tal como aparece en las figuras anteriores. intersecciones de 2°. Pueden ser expuestas también definiéndolas algebraicamente mediante la ecuación general de segundo grado: Ax2 + Bxy + Cy2 + Dx + Ey + F = 0 3°. Podemos optar otra vía, presentándolas como lugares geométricos de puntos que satisfacen ciertas propiedades geométricas. Nosotros procederemos a plantear las dos últimas, empezando por la tercera forma. Es decir, como lugares geométricos. Cada una de las cónicas se definirán primeramente sin coordenadas; esto es, no dependerá de las coordenadas que se elija. B. La recta real. El objetivo fundamental de la geometría analítica consiste en crear representaciones visuales de los conceptos matemáticos mediante el uso de los sistemas de coordenadas. Así tenemos, el sistema de coordenadas que utilizamos para representar los números reales de R se llama recta real. El número real que corresponde a un punto particular de la recta real se llama coordenada del punto. (–) -7/2 • -5 -4 -3 -2 -3/4 • -1 0 π • 3 • 1 2 3 (+) R 4 5 Fig. 8 Lic. José L. Estrada P. UNAJMA Cónicas – La recta 4 Cada punto de la recta real corresponde a uno y sólo a uno de los números reales, y recíprocamente. Esta relación se denomina correspondencia uno a uno. En la figura 8, aparecen los puntos: –7/2, –3/4, 3 , π . C. Distancia entre dos puntos de la recta real. La distancia d entre dos puntos x1 y x2 de la recta real viene dada por: d = x 2 − x1 = (x 2 − x 1 )2 Ejemplo 1. ¿Qué intervalo de la recta real contiene todos los números que se encuentran a no más de tres unidades del 4? Solución: Sea x un punto cualquiera de este intervalo. Se quiere hallar todos los x tales que la distancia entre “x” y 4 es menor o igual que 3; es decir, |x – 4| ≤ 3. Desde que |x – 4| ≤ 3 ⇔ –3 ≤ x – 4 ≤ 3 ⇔ 1 ≤ x ≤ 7, entonces x se encuentra en el intervalo cerrado [1,7]. Véase la figura 9 (–) • 0 [ 1 3 unidades 3 unidades • 4 Fig. 9 ] 7 (+) R Ejemplo 2. Hállese el punto medio y los puntos de trisección del intervalo [4,12] Solución: Lic. José L. Estrada P. UNAJMA Cónicas – La recta 5 La coordenada del punto medio c entre a y b, viene dada por: x = (a) adelante), donde r = x1x xx 2 1. En otras palabras, x = x1 • a=4 1 = = 1 es la razón del segmento (dirigido) x 1 x y del segmento xx 2 , que ambos son iguales a 1 x1 + x 2 4 + 12 = 8 . Ver la figura 10. ; es decir, c = 2 2 x • 1 x 1 + rx 2 (la demostración la veremos más 1+ r c=8 Fig. 10 1 x2 • x1 • b = 12 a=4 x = 20/3 • 1 x’ = 28/3 • 2 Fig. 11 (b) El 1er. Punto de trisección x entre x1 y x2 también está dado por x = x2 • b = 12 x 1 + rx 2 , donde 1+ r segmentos x 1 x y x x 2 , que están en la relación de 1 a 2 respectivamente, luego r = El segundo punto de trisección x ' viene dado por x ' = (c) x ' = 4 + 2(12) 1+ 2 = 28 r= x1x es la razón de los x x2 1 ; esto es, 2 x= ( )( ) = 20 . ( ) 3 4 + 1 / 2 12 1+ 1/ 2 x 1 + rx 2 x x' 2 , donde r = 1 = ; luego 1+ r x′ x 2 1 . Ver figura 11. 3 Lic. José L. Estrada P. UNAJMA Cónicas – La recta 6 EJERCICIOS 1. Hallar los intervalos de la recta real que contienen todos los números que están a más de tres unidades del –2. 2. Se quiere dividir el intervalo [-2,7] en 5 subintervalos colocando 4 puntos y1, y2, y3, y4 interiormente. Halle las coordenadas de y1, y2, y3, y4. 10.2 La línea recta en el plano R2 Generalmente la geometría analítica empieza su estudio con la línea recta desde el punto de vista geométrico, debido a que su ecuación es la más sencilla; estas ecuaciones desde el punto de vista algebraico tuvo lugar en el capitulo 1. Allí consideramos una ecuación lineal con una, dos, tres y más variables. Recordemos, una línea recta con dos variables en el plano tiene como ecuación a las siguientes formas: 1. 2. 3. ax + by + c = 0 y = mx + b y – y0 = m(x – x0) 4. y − y1 = 5. x y + =1 a b 6. y 2 − y1 x 2 − x1 x x1 y y1 1 1 =0 x2 y2 1 Lic. José L. Estrada P. (x − x1 ) : : : Ecuación general (a y b no son ambos ceros) Ecuación de pendiente - intersección Ecuación de punto - pendiente : Ecuación de dos puntos : Ecuación en forma simétrica : Ecuación en forma de determinante UNAJMA Cónicas – La recta 7 En efecto, de 4 se tiene (y – y1) (x2 – x1) = (y2 – y1) (x – x1), de donde x (y1 – y2) – y (x1 – x2) + 1(x1y2 – x2y1) = 0. Esta ecuación no es sino el desarrollo del determinante de tercer orden por el método de cofactores a lo largo de la primera fila; esto es, se tiene la ecuación 6. (cos ω)x + (sen ω)y – p = 0 : 7. Ecuación en forma normal. El número p es positivo y representa la longitud de la normal trazada desde el origen a la recta. y ω el ángulo positivo menor de 360° medido a partir de la parte positiva del eje x a la normal. En efecto; es evidente que, para un par cualquiera del valor de p y ω, la recta L trazada por P1 = (x1, y1) perpendicular a OP1 queda perfectamente determinada. Véase la figura 12 y L y P2=(x2,y2) • P1=(x1,y1) • y1 • d p ω • x1 O Fig. 12 x • P1=(x1, y1) • B x Fig. 13 Sabemos que x1 = p cos ω, y1 = p sen ω, donde p = x12 + y12 . Luego: P1 = (p cos ω , p sen ω). Como la pendiente del segmento OP1 está dada por m1 = tan ω, la pendiente de L es cos ω 1 . Reemplazando en la ecuación y – y1 = m2 = − = − cot ω = − tan ω sen ω Lic. José L. Estrada P. UNAJMA Cónicas – La recta 8 cos ω (x − p cos ω) ; es decir: x cos ω + y sen ω–p = 0. sen ω En seguida se exponen varios resultados que serán de mucha utilidad. m(x – x1) se tiene y – p sen ω = − A. Distancia entre dos puntos del plano La distancia d entre dos puntos dados P1 = (x1,y1), P2 = (x2,y2) del plano R2 viene dada por: d= (x 2 − x1 )2 + (y 2 − y1 )2 En efecto: Sean los puntos P1 y P2 como se muestra en la figura 13. Observando dicha figura, la distancia de B a P2 es d(B,P2) = |y2 – y1| y la distancia de P1 a B es d(P1,B) = |x2 – x1|. Aplicando el teorema de Pitágoras en el triángulo P1BP2 se tiene d= (P1P2 )2 = x 2 − x1 2 + y 2 − y1 2 , de donde (x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 . B. División de un segmento en una razón dada Si P1 = (x1,y1) y P2 = (x2,y2) son los extremos de un segmento de recta P1P2 , las coordenadas (x,y) de un punto P que divide a este segmento en la razón dada Lic. José L. Estrada P. UNAJMA Cónicas – La recta 9 x + r x2 x= 1 1+ r PP r = 1 son: PP2 y + r y2 y= 1 1+ r (r ≠ –1) PP A A Demostración: Por la geometría elemental sabemos que r = 1 = 1 , de donde A1A = x − x 1 , AA 2 = x 2 − x , luego PP2 reemplazando se tiene r = AA 2 x−x 1 . Despejando x se tiene x = x1 + r x 2 . Análogamente se deduce que y = y1 + r y 2 . En 1+ r 1+ r x −x 2 ambos casos r ≠ –1. Ver figura 14 P2 = (x2, y2) y L1 • B2 B B1 y • P=(x, y) • θ2 C P1=(x1, y1) A1 A θ θ1 A2 Fig. 14 x • A α1 Fig. 15 α2 • B L2 x C. Coordenadas del punto medio En el caso particular de que r = 1; es decir, P es el punto medio del segmento dirigido P1P2 , entonces las coordenadas de P son: Lic. José L. Estrada P. UNAJMA Cónicas – La recta 10 y + y2 y= 1 2 x + x2 x= 1 2 D. Angulo entre dos rectas El ángulo que forman dos rectas L1 y L2, está dado por: tan θ = m 2 − m1 1 + m1 m 2 donde m1 es la pendiente de la recta inicial y m2 es la pendiente de la recta final correspondiente al ángulo θ. En efecto: sean θ1 y θ2 los ángulos suplementarios. Ver figura 15. Para el ángulo θ1 consideramos la recta inicial L1 cuya pendiente es m1, y la recta final L2 con pendiente m2. Para el ángulo θ2, L2 es la inicial y L1 la final. Por la geometría elemental se conoce que en el triángulo ABC: “Un ángulo exterior es igual a la suma de los otros dos ángulos interiores”; esto es, α2 = α1 + θ1, de donde θ1 = α2 – α1. Luego tan θ1 = tan (α 2 − α1 ) = tan α 2 − tan α1 1 + tan α 2 tan α1 . Como m1 = tan α1 , m2 = tan α2, se tiene: m 2 − m1 . Análogamente, si consideramos el ángulo exterior θ2, resulta θ2 = α1 + (180 – α2). Otra vez tomando 1 + m1 m 2 la tangente trigonométrica en ambos miembros, y empleando la fórmula de tangente de una suma de dos ángulos, se tiene: tan θ1 = tan θ 2 = tan θ 2 = ( ) tan α1 − tan α 2 , o lo que es lo mismo: = 1 − tan α1 tan (180 − α 2 ) 1 + tan α1 tan α 2 tan α1 + tan 180 − α 2 m1 − m 2 1 + m1 m 2 . Comparando tan θ1 y tan θ2 (pues tan θ1 = – tan θ2), se obtiene la fórmula tan θ = m 2 − m1 1 + m1 m 2 , m1 m2 ≠ –1. Lic. José L. Estrada P. UNAJMA Cónicas – La recta 11 E. Rectas paralelas. “Dos rectas no verticales y distintas son paralelas si y sólo si sus pendientes son iguales” Demostración: Dos rectas son paralelas cuando el ángulo formado por ellos es 0° o 180°. En cualquiera de los dos casos, del resultado D se tiene tan θ = m 2 − m1 de donde 1 + m1 m 2 m1 = m2 F. Rectas perpendiculares “Dos rectas no verticales son perpendiculares si y sólo si sus pendientes satisfacen En efecto: Cuando las dos rectas forman un ángulo de θ = 90°, entonces la fórmula tan θ = Tómese cot θ = 1 + m1 m 2 m 2 − m1 . Desde que cot 90° = 0, entonces 0 = 1 + m1 m 2 m 2 − m1 de donde m1 m2 = –1. m 2 − m1 1 + m1 m 2 no se puede aplicar. m1 m2 = –1 Ejemplo 1. Los puntos medios de los lados de un triángulo son (2,5), (4,2) y (1,1). Hallar las coordenadas de los tres vértices. Solución: Sean A = (x1,y1), B = (x2,y2), C = (x3,y3) los tres vértices del triángulo. Ver figura 16. Por la fórmula de las coordenadas del punto medio se tienen: x + x3 y + y3 x + x3 y + y3 x1 + x 2 y + y2 = 1, 1 = 1, 1 = 2, 1 = 5, 2 = 4, 2 = 2 . Agrupando las 6 ecuaciones precedentes en 2 2 2 2 2 2 dos sistemas de ecuaciones lineales de tres variables se tienen: Lic. José L. Estrada P. UNAJMA Cónicas – La recta 12 x 1 + x 2 = 2 x 1 + x 3 = 4 x + x = 8 3 2 y1 + y 2 = 2 y1 + y 3 = 10 y + y = 4 3 2 ... (1) ... (2) ... (3) ... (4) ... (5) ... (6) Resolviendo el 1er. sistema: (1) + (2) : (1) + (3) : (2) + (3) : 2x1 + (x2 + x3) = 6 ⇒ 2x1 + 8 = 6 ⇒ x1 = –1 (x1 + x3) + 2x2 = 10 ⇒ 4 + 2x2 = 10 ⇒ x2 = 3 (x1 + x2) + 2x3 = 12 ⇒ 2 + 2x3 = 12 ⇒ x3 = 5 Resolviendo el 2do. sistema. Análogamente se obtiene y1 = 4, y2 = –2, y3 = 6. Por tanto = (5,6). A = (–1,4) , B = (3,–2) , C y (2,5) C=(x3, y3) • A=(x1, y1) • (4,2) (1,1) • x B=(x2, y2) Fig. 16 Lic. José L. Estrada P. UNAJMA Cónicas – La recta 13 G. Conversión de la forma general a la forma normal. Sea L una recta de ecuación general Ax + By + C = 0, y de ecuación normal (cos ω)x + (sen ω)y – p = 0. Como ambas ecuaciones representan la misma recta, sus coeficientes deben ser proporcionales: cos ω = kA ... (1) sen ω = kB ... (2) – p = kC ... (3) 1 Elevando al cuadrado ambos miembros de (1) y (2), y sumándolos se obtiene k = ± A 2 +B 2 . ¿Qué signo debe elegirse?. En efecto: 1° Si C ≠ 0, de la ecuación (3) se deduce que k y C deben ser de signo opuesto. 2° Si C = 0 y B ≠ 0, de la ecuación (2) se infiere que k y B deben ser del mismo signo, puesto que sen ω ≥ 0 (0 ≤ ω < 180°) 3° Si C = 0, B = 0, de la ecuación (1) se afirma que k y A deben ser también del mismo signo, puesto que cos ω = 1 (ω = 0°) Ejemplo 2. La ecuación de una recta es 12x – 5y – 52 = 0. Reducir a su forma normal, y hallar los valores de p y ω. 1 Solución: Como A = 12, B = –5, C = –52, entonces k = + A cos ω = 12 13 , sen ω = kB implica senω = − Lic. José L. Estrada P. 5 13 , y – p = kC ⇒ − p = − 2 +B 52 13 2 = 1 144 + 25 = 1 . Luego cos ω = kA implica 13 , es decir, p = 4. Desde que cos ω = (+), y sen ω = UNAJMA Cónicas – La recta 14 (–), ω está en el 4to. cuadrante. Pero de la ecuación cos ω = 12 13 empleando una calculadora de bolsillo se obtiene 22° 37’ 11’’ de donde: ω = (359° 59’ 60’’) – (22° 37’ 11’’) = 337° 22’ 49’’. Por lo tanto, la ecuación de la recta en su forma normal es: 12 13 x− 5 13 y−4=0. H. Distancia de un punto a una recta Sea L la recta de ecuación normal (cos ω)x + (sen ω)y – p = 0 y P1 = (x1, y1) un punto no situado en L y d = d(P1 , L) la distancia de P1 a L. Sea L1 la recta que pasa por P1 y es paralela a L, y p1 la distancia (positiva) desde el origen a la recta L1 tal como puede verse en la figura 17 y y B • N • P1=(x1,y1) A • p d L1 ω x O L Fig. 17 Por definición d 0A = p, • P1= (x1,y1) B • ω L1 A • N x L Fig. 18 0B = p1. A y B son puntos de intersección de L y L1 con la normal (positiva) 0 N respectivamente. Además d = AB , y para segmentos dirigidos se tiene: AB = 0 B − 0 A = p1 – p > 0, (p1 > p). Ahora la ecuación normal de L1 es (cos ω)x + (sen ω)y–p1 = 0, y como P1 = (x1,y1) está sobre L1, entonces: (cos ω)x1 + (sen ω)y1 – p1 = 0; es decir, p1 = (cos ω)x1 + (sen ω)y1. Lic. José L. Estrada P. UNAJMA Cónicas – La recta 15 Desde que AB = p1 − p ⇒ AB = (cos ω) x 1 + (senω) y1 − p > 0 . Puesto que d = AB , entonces d = | (cos ω)x1 + (sen ω)y1 – p |. Por tanto para hallar d, las coordenadas x1 y y1 se sustituyen en la ecuación normal de L. Ahora, al convertir la ecuación general Ax + By + C = 0 a su ecuación normal se tiene: Ax + By + C ± A 2 + B2 = 0 , es decir: d= Ax 1 + By1 + C A 2 + B2 Por tanto, para obtener d, basta sustituir las coordenadas del punto P1 = (x1,y1) en la ecuación general de la recta L. Hemos demostrado prácticamente un teorema importante de la geometría analítica. Nota: 1. Existen naturalmente diferentes posiciones que adoptan las rectas L, L1 y el punto P1. De posiciones. Con un conveniente arreglo se llegan al mismo resultado. 2. Cuando se requiere hallar la distancia dirigida d, entonces d = Ax 1 + By1 + C 2 ± A +B 2 hecho existe en total 6 ; donde el signo se determina de acuerdo con los 3 casos expuestos en la sección G de 10.2. 3. d = AB se considera positiva cuando P1 y el origen de coordenadas están en lados opuestos de la recta L, tal como aparece en la figura 17. En cambio − d = AB se toma negativo cuando P1 y el origen se encuentran en el mismo lado de la recta L. Véase por ejemplo la figura 18. Ejemplo 3. En la ecuación ax + 3y + 5 = 0. Hallar el valor del coeficiente a de manera que la distancia dirigida de la recta que representa al punto (2,–2) sea igual a –1. Lic. José L. Estrada P. UNAJMA Cónicas – La recta 16 Solución: Desde que: A = a, B = 3 y C = 5 = (+), entonces k = (–); es decir k = − d= Ax1 + By1 + C − A 2 +B 2 ⇒ −1 = a ( 2) + 3( −2) + 5 − a 2 ecuación cuadrática se tiene: a = 1 coeficiente a = 2+2 7 3 1 a2 + 9 , luego la distancia a 2 + 9 = 2a − 1 , simplificando 3a – 4a – 8 = 0. Resolviendo esta 2 es decir +9 2+2 7 3 , a2 = 2−2 7 3 . La raíz a2 no satisface la ecuación a 2 + 9 = 2a − 1 , luego el es la solución del problema. I. Bisectrices de ángulos suplementarios. La bisectriz de un ángulo es aquella recta que pasa por el punto de intersección y divide el ángulo en dos partes iguales. Dada dos rectas que se cortan L : Ax +By + c = 0, L’ : A’x + B’y + C’ = 0, queremos hallar las ecuaciones de las bisectrices L1 , L2 de los ángulos suplementarios. Ver figura 19. Cualquier punto P = (x, y) sobre las bisectrices se cumple |d1| = |d2|; es decir, son numéricamente iguales; pero para hallar sus ecuaciones consideraremos la distancias dirigidas: (a) Para P = (x, y) sobre L2 la distancia d1 es positiva, ya que el punto P y el origen de coordenadas se encuentran en lados opuestos de la recta L. Análogamente, d2 es también positiva, puesto que P y O se encuentran en lados opuestos de la recta L’. De aquí que d1 = d2. (b) Para P = (x, y) sobre L1, d1 es positiva y d2 es negativa (P y O están en un mismo lado de la recta L’). De aquí que d1 = –d2. En consecuencia, la ecuación de L2 viene dada por : d1 = d 2 ⇒ Lic. José L. Estrada P. Ax + By + C ± A 2 + B2 = A ' x + B' y + C' ± A ' 2 + B' 2 UNAJMA Cónicas – La recta La ecuación de L1, queda expresada por: 17 d1 = −d 2 ⇒ Ax + By + C ± A 2 + B2 =− A ' x + B' y + C' ± A ' 2 + B' 2 Los signos se eligen de acuerdo a las 3 partes de la sección G(conversión de la forma general a la forma normal). y L’ P=(x,y) • d2 d1 d2 • P=(x,y) d1 L • L2 x O Fig. 19 L1 Ejemplo 4. (a) Hallar la ecuación de la bisectriz del ángulo agudo formado por las rectas x – 2y – 4 = 0 y 4x – y – 4 = 0 (b) Un punto se mueve de tal manera que su distancia del punto (1,–1) es siempre igual al doble de su distancia de la recta 3x – 2y + 6 = 0. Hallar la ecuación en su lugar geométrico. Solución: (a) Sean las rectas L : x – 2y – 4 = 0, L’ : 4x – y – 4 = 0, y L’’ la recta bisectriz. Véase la figura 20. Las distancias dirigidas son –d1 y d2, luego Lic. José L. Estrada P. UNAJMA Cónicas – La recta − x − 2y − 4 + 12 + 2 2 ( = 18 4x − y − 4 + 4 2 + 12 . Reduciendo esta ecuación se tiene: ) ( ) ( ) 17 + 4 5 x − 2 17 + 5 y − 4 17 + 4 5 = 0 y L’ y O d2 L” • P=(x,y) d1 2d L • P = (x,y) d • P0 = (1,–1) x • L x Fig. 21 Fig. 20 (b) Trazamos la recta L : 3x – 2y + 6 = 0 y el punto fijo P0 = (1,–1). Sea P = (x, y) un punto móvil que da origen a una curva, llamada el lugar geométrico. Ahora: (Ver figura 21) ( ) (x − 1)2 + (y + 1)2 , d P, P0 = d(P, L ) = 3x − 2 y + 6 2 2 3 +2 , Según el enunciado del problema se tiene: d(P, P0 ) = 2d ( P, L) Lic. José L. Estrada P. UNAJMA Cónicas – La recta 19 3x − 2 y + 6 ; es decir 13 (x − 1)2 + (y + 1)2 = 2 3x − 2 y + 6 . Elevando al cuadrado ambos 3 2 + 2 2 miembros y simplificando obtenemos: 23x2 – 48xy + 3y2 + 170x – 122y + 118 = 0. (x − 1)2 + (y + 1)2 = 2 J. Área de un triángulo Deseamos determinar una fórmula mediante la cual se pueda obtener el área de un triángulo cualquiera conociendo las 3 coordenadas de los 3 vértices. En efecto, sean A = (x1, y1), B = (x2 , y2) y C = (x3 , y3) los vértices del triángulo ABC. Ver la figura 22. y • y B=(x2,y2) P L h x • A=(x1,y1) b Fig. 22 • A=(x1,y1) • • B=(x2,y2) G • Q R C=(x3,y3) Lic. José L. Estrada P. (x 1 − x 3 )2 + (y1 − y 3 )2 C=(x3,y3) x Fig. 23 Sabemos por geometría elemental, que el área de un triángulo es S = segmento AC, dado por b = • 1 bh , donde la base b es la longitud del 2 , y la altura h es la distancia del punto B a la recta L que pasa por A y UNAJMA Cónicas – La recta 20 C. Pero la ecuación de L está dado por: y − y 1 = y1 − y 3 (x − x 1 ) ; es decir: (y1 – y3)x – (x1 – x3)y + (x1y3 – x3y1) = 0, luego x1 − x 3 la distancia de B a L viene dada por: (y1 − y 3 )x 2 − (x 1 − x 3 )y 2 + (x 1 y 3 − x 3 y1 ) . h= (y1 − y 3 )2 + (x 1 − x 3 )2 Reemplazando los valores de b y h en S resulta 1 (y1 − y 3 )x 2 − (x 1 − x 3 )y 2 + (x 1 y 3 − x 3 y1 ) . Examinando esta expresión se deduce que es el desarrollo del 2 determinante de 3er. orden: S= x1 1 S= x2 2 x3 y1 1 y2 1 y3 1 Ejemplo 5. Dado el triángulo con vértices A = (–3,2), B = (7,3), C = (1,–3) (a) Hallar el área del triángulo (b) Encuentre las coordenadas del baricentro Solución: (a) El área de x1 1 S= x2 2 x3 un triángulo conocido sus vértices (x1,y1) , (x2,y2) , (x3,y3) viene dado y1 1 −3 1 y 2 1 , lo cual reemplazado los vértices de A, B y C resulta: S = 7 2 y3 1 1 por el valor absoluto de : 2 1 3 1 = −27 , luego el área −3 1 es S = 27 unidades cuadradas. Lic. José L. Estrada P. UNAJMA Cónicas – La recta 21 Existe otra fórmula para hallar S por medio de un determinante de 2do. orden. En efecto: el desarrollo de S es 1 S = (x 2 y 3 − x 3 y 2 − x 1 y 3 + x 3 y 1 + x 1 y 2 − x 2 y 1 ) . Aumentando y disminuyendo el producto x1y1 y reordenando se 2 obtiene: 1 S = [(x 2 y 3 − x 1 y 3 ) − (x 2 y 1 − x 1 y 1 ) − (x 3 y 2 − x 1 y 2 ) + (x 3 y 1 − x 1 y 1 )] . Factorizando: 2 1 S = [(x 2 − x 1 )(y 3 − y 1 ) − (x 3 − x 1 )(y 2 − y 1 )] . Esta expresión no es sino el desarrollo del determinante 2 × 2 : 2 S= 1 x 2 − x1 2 x 3 − x1 y 2 − y1 y3 − y1 Podríamos otra vez hallar el área del triángulo con los vértices: A = (x1 , y1) = (–3,2), B = (x2 , y2) = (7,3), C = (x3 , y3) = (1,–3): S= 1 1 7 − (−3) 3 − 2 1 10 = = −27 ; es decir, el área es 27u2. 2 1 − (−3) − 3 − 2 2 4 −5 (b) Como ya sabemos, la intersección común de las 3 medianas de un triángulo se llama baricentro, y se encuentra en el punto de trisección más cercano al punto medio del lado correspondiente. Vamos a determinar las coordenadas del baricentro G = (x , y). En efecto, sean los vértices A = (x1 , y1), B = (x2 , y2), C = (x3 , y3). P es un punto medio de AB . Lic. José L. Estrada P. UNAJMA Cónicas – La recta 22 1 PG 1 x + x 2 y1 + y 2 Véase la figura 23. P = 1 , = ; es decir, el segmento está dividido en la razón r = , . Pero 2 2 2 2 GC x + rx 2 y + ry 2 luego de la fórmula: x = 1 y y= 1 se tiene para G: 1+ r 1+ r x1 + x 2 + rx 3 x 1 + x 2 + 1 x 3 2 x + x2 + x3 2 2 x= = = 1 1 1+ r 3 1+ 2 y1 + y 2 y1 + y 2 1 + ry 3 + y3 2 y + y2 + y3 2 2 . y= = = 1 1 1+ r 3 1+ 2 En consecuencia las coordenadas de G es: x + x 2 + x 3 y1 + y 2 + y 3 G= 1 , 3 3 Para hallar las coordenadas en nuestro problema, sólo nos queda reemplazar las coordenadas de los 3 vértices; es decir: − 3 + 7 +1 2 + 3 − 3 5 2 G= , = , . 3 3 3 3 Ejemplo 6. Los vértices de un triángulo son A = (–6,–2), B = (6,1), C = (2,4). Se traza la bisectriz del ángulo exterior correspondiente al ángulo interno ACB. La bisectriz corta a la prolongación del lado AB en el punto D. Hállese las coordenadas de D. Lic. José L. Estrada P. UNAJMA Cónicas – La recta 23 Solución: De la figura 24 podemos deducir rápidamente que las pendientes de L1, L2 y L3 son respectivamente: y 4+2 3 = 2+6 4 1+ 2 1 m2 = = 6+6 4 1− 4 3 m3 = =− 6−2 4 L1 m1 = L C=(2 , 4) • D=(18,4) θ θ • • L2 B=(6,1) x • A=(-6,-2) Fig. 24 L3 Sea L la bisectriz exterior del ángulo ACB donde m es su pendiente. Como tan θ = m − m3 m1 − m . Reemplazando = 1 + m 1 m 1 + mm 3 3 3 , m 2 = − se obtiene la ecuación cuya solución es m = 0. Luego la ecuación de L es: y – 4 = m(x – 2) ⇒ y – 4 = 4 4 y−4 = 0 1 0. Por otra parte la ecuación de L2 es: y − 1 = (x − 6 ) ⇒ x − 4 y − 2 = 0 . Resolviendo el sistema se obtiene 4 x − 4 y − 2 = 0 el punto de intersección D = (18, 4). m1 = Lic. José L. Estrada P. UNAJMA Cónicas – La recta 24 EJERCICIOS 1. Las ecuaciones de los lados de un triángulo son 5x – 7y + 27 = 0 , 9x – 2y – 15 = 0, 4x + 5y + 11 = 0. Hallar sus ángulos y comprobar sus resultados. 2. Dado el triángulo de vértices A = (– 2, 1), B = (4,7), C = (6,– 3): (a) Hallar las ecuaciones de los lados. (b) Hallar las ecuaciones de las rectas que pasan por el vértice B y trisecan al lado opuesto AC. (c) Hallar los vértices del triángulo formado por las rectas que pasan por los vértices A, B y C, y son paralelas a los lados opuestos. 3. Hallar las ecuaciones de las medianas y las coordenadas de su punto de intersección, en el ejercicio 2. El punto de intersección se llama baricentro del triángulo. (La mediana de un triángulo es el segmento de recta que une un vértice con el punto medio del lado opuesto). 4. Hallar las ecuaciones de las mediatrices de los lados y las coordenadas de su punto de intersección en el ejercicio 2. El punto de intersección se denomina circuncentro del triángulo. (La mediatriz de un lado de un triángulo es el segmento de recta perpendicular trazada del punto medio de dicho lado). 5. Hallar las ecuaciones de las alturas y su punto de intersección, del ejercicio 2. Este punto de intersección recibe el nombre de ortocentro del triángulo. (La altura del triángulo es el segmento de recta trazada por un vértice y perpendicular al lado opuesto). 6. Hallar las ecuaciones de las bisectrices de los ángulos interiores del triángulo y las coordenadas de su punto de intersección del ejercicio 2. Este punto de intersección se llama incentro del triángulo, y equidista de los 3 lados. (La bisectriz del triángulo es el segmento de recta trazado de un vértice y divide al ángulo en dos partes iguales). Lic. José L. Estrada P. UNAJMA Cónicas – La recta 25 7. Los vértices de un triángulo son (1,1), (4,7), (6,3). Demostrar que el baricentro, el circuncentro y el ortocentro son colineales. (En general este resultado se cumple para cualquier triángulo. La recta que une estos tres puntos se llama La recta de EULER). 8. Demostrar que una condición necesaria y suficiente para que tres puntos diferentes de coordenadas (x1 , y1), (x2 , y2), (x3 , y3) sean colineales es que: x1 y1 1 x 2 y2 1 = 0 x 3 y3 1 9. Desde el punto (6,0) se trazan perpendiculares a los lados 5x–y–4=0, y=1,x–y–4=0 de un triángulo. Verifique que los pies de estas perpendiculares son colineales. 10. (a) Determinar el valor de b para que la distancia del origen a la recta x+by–7 = 0 sea 2. (b) Hallar la ecuación de la recta cuya distancia del origen es 5 y que pasa por el punto (1,7). 11. (a) Hallar la forma normal de la ecuación de la recta que es paralela a la recta x – 5y + 11 = 0 y pasa por el punto A = (–7,2). (b) Hallar la ecuación de la recta que es paralela a la que tiene por ecuación 3x+2y–9=0 y cuya distancia del origen es 8. 12. (a) Los vértices de un triángulo son A = (–4,1), B = (–3,3), C = (3,–3). Hallar la longitud de la altura del vértice A sobre el lado BC y el área del triángulo. (b) Hallar la distancia entre las rectas paralelas x + 2y – 10 = 0 y x + 2y + 6 = 0. Lic. José L. Estrada P. UNAJMA Cónicas – La recta 26 13. (a) Hallar la ecuación del lugar geométrico de un punto que se mueve de tal manera que su distancia de la recta 4x – 3y + 12 = 0 es siempre igual al doble de su distancia del eje x. (b) Hallar la ecuación del lugar geométrico de un punto que se mueve de tal manera que su distancia de la recta 4x – 3y + 12 = 0 es siempre igual a la mitad de su distancia del eje y. 14. Hallar las ecuaciones de las bisectrices de los ángulos formados por las rectas x + y –1 = 0, 2x – y + 1 = 0, y demostrar que son perpendiculares. 15. En el triángulo de vértices (–4,1), (–3,3), (3,–3); hallar las ecuaciones de las bisectrices de los ángulos interiores, y demostrar que concurren en punto. 16. (a) Hallar la ecuación del lugar geométrico de un punto que se mueve de tal manera que su distancia de la recta x – 2 = 0 es siempre 3 unidades mayor que su distancia del punto (–1 ,–3). Trazar el lugar geométrico. (b) Un punto se mueve de tal manera que su distancia de la recta x + y + 1 = 0 es siempre igual a su distancia del punto (–2,–1). Hallar la ecuación de su lugar geométrico. 16. (a) Hallar el área del triángulo cuyos vértices son A = (–1,1), B = (3,4), C = (5,–1). (b) Hallar la ecuación de la recta de Euler para el triángulo de la parte (a). 17. Determinar el valor de la constante b para que las 3 rectas 8x +3y–1= 0, 3x+ by–3 = 0, x – 5y + 16 = 0 sean concurrentes. 18. Se tiene un triángulo con vértices A = (2,–4), B = (9,9), C = (10,2). Halle la ecuación de la recta que pasa por el baricentro del triángulo ABC y es paralela al lado AC. 19. La recta L1 pasa por los puntos A = (10,9), B = (2,3). La recta L2 pasa por los puntos A = (10,9), C = (3,–15). Halle la pendiente de la recta bisectriz del ángulo agudo que forma L1 y L2. Lic. José L. Estrada P. UNAJMA Cónicas – La recta 27 20. Una recta pasa por la intersección de las rectas 2x – 3y = 5, x + 2y = 13 y tiene como intersección con el eje x el punto cuya primera coordenada es dos veces su pendiente. Encontrar la ecuación de dicha recta. 21. Hallar las ecuaciones de las bisectrices de los ángulos formados por las rectas: x + y –1=0 y 2x – y + 1 = 0. Demostrar, además que son perpendiculares entre sí. 22. Determinar la ecuación de una recta que pasa por el punto D = (–2,3) y sea perpendicular a la bisectriz interior del triángulo de vértices A = (0,0), B = (4,8), C = (6,2) relativa al vértice B. 23. Dado los puntos A = (1,1), B = (9,7), se pide determinar las coordenadas de un punto C pertenecientes a la recta L: y = x – 6, tal que el ángulo ACB sea ángulo recto. Lic. José L. Estrada P. UNAJMA UNAJMA