Un poco de historia…
Anuncio

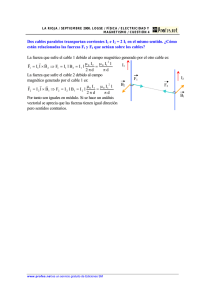
DEPARTAMENTO DE FISICA Magnetismo y Electromagnetismo Ejercitación Un poco de historia… Nikola Tesla (1856 - 1943) Tras su demostración de comunicación inalámbrica por medio de ondas de radio en 1894 y después de su victoria en la “guerra de las corrientes”, fue ampliamente reconocido como uno de los más grandes ingenieros eléctricos de los EE. UU. de América. Gran parte de su trabajo inicial fue pionero en la ingeniería eléctrica moderna y muchos de sus descubrimientos fueron de suma importancia. Durante este periodo en los Estados Unidos la fama de Tesla rivalizaba con la de cualquier inventor o científico en la historia o la cultura popular, pero debido a su personalidad excéntrica y a sus afirmaciones aparentemente increíbles y algunas veces casi inverosímiles, acerca del posible desarrollo de innovaciones científicas y tecnológicas, Tesla fue finalmente relegado al ostracismo y considerado un científico loco. James Clerk Maxwell (1831 - 1849) Físico escocés conocido principalmente por haber desarrollado la teoría electromagnética clásica, sintetizando todas las anteriores observaciones, experimentos y leyes sobre electricidad, magnetismo y aun sobre óptica, en una teoría consistente. Las ecuaciones de Maxwell demostraron que la electricidad, el magnetismo y hasta la luz, son manifestaciones del mismo fenómeno: el campo electromagnético. Michael Faraday (1791 - 1867) En 1831 trazó el campo magnético alrededor de un conductor por el que circula una corriente eléctrica, y ese mismo año descubrió la inducción electromagnética, demostró la inducción de una corriente eléctrica por otra, e introdujo el concepto de líneas de fuerza para representar los campos magnéticos. Durante este mismo periodo, investigó sobre la electrólisis y descubrió las dos leyes fundamentales que llevan su nombre. ORT 2013 1 1) Tres imanes con forma de disco se encuentran uno sobre otro y, como muestra la figura, se mantienen en esa posición debido a una varilla de madera que los atraviesa. La cara superior del imán que está arriba corresponde a un polo Norte. a) ¿Cuáles son los polos de las caras superiores de los otros discos? b) ¿La base es también un imán? 2) En la siguiente figura se muestra la disposición de las limaduras de hierro al ser arrojadas sobre un cartón colocado sobre un imán. Esquematizar el vector campo magnético (B) en cada uno de los puntos indicados. C D E N S A 3) Se colocaron 4 brújulas alrededor de un imán como se muestra en la figura. Indicar la orientación de cada una de ellas. Brújula La figura de abajo representa la brújula. Indicar la orientación de la aguja. N S 4) Se tienen dos barras de hierro exactamente iguales en forma, tamaño, color, peso, etc. Una es un imán y la otra no. Si no se dispone de ningún otro elemento excepto las dos barras, ¿cómo se puede averiguar cuál de las dos es el imán? ORT 2013 2 Campo producido por un cable por donde circula corriente La intensidad del campo magnético generado alrededor de un cable por el cual circula corriente se puede calcular a través de la relación: B 2 I r donde I es la corriente que circula por el cable r es la distancia medida desde el cable al punto en donde se calcula el campo magnético es una constante igual a 1.10-7 Tm/A Y la dirección del campo está dada por la regla de la mano derecha: Ejemplo: Calcular el campo magnético producido por un alambre por el que circula una corriente de 2A en dirección saliente del papel, en los puntos P, Q, R y S. Dato: r1=5cm, r2=8cm El campo magnético de todos los puntos que están sobre cualquier circunferencia concéntrica con el cable, será de la misma intensidad. En la figura se muestran como ejemplo dos circunferencias: la roja de radio r1 y la azul de radio r2. Todos los puntos de la circunferencia roja tendrán la misma intensidad de campo magnético, pero distinta dirección. Así, por ejemplo, el campo magnético en los puntos S y R tiene la dirección indicada por el vector, y se ve que apuntan para distinto lado, pero la intensidad del campo es la misma, y se puede calcular de acuerdo a la ecuación dada anteriormente. B(S) B(R ) 2 * 10 7 Tm / A * 2A 810 6 T 0,05m Corriente saliente del papel R r1 P r2 S Q Calcular el campo magnético en los puntos que faltan (P y Q) ORT 2013 3 ¿Qué pasa cuando hay más de un alambre? En cada punto del espacio se sentirá un campo magnético debido a la presencia de cada “fuente” de campo. El campo magnético total en un punto del espacio será la SUMA VECTORIAL de los campos magnéticos producidos por cada tipo de configuración. 5) En la figura se muestran dos brújulas: una sobre el cable y la otra por debajo. Cuando se cierra la llave, indicar: a) ¿Para qué lado circulará la corriente eléctrica? b) ¿Cómo se orientará cada una de las agujas magnéticas de las brújulas? (La zona sombreada corresponde al polo norte de la aguja). + - 6) Los diagramas corresponden a un conductor rectilíneo por donde circula una corriente eléctrica, visto desde tres posiciones diferentes. Representar en cada caso el vector Campo Magnético en los puntos “A” y “C”. A A Vista Lateral I Vista Frontal I C C A Vista en Perspectiva I C 7) Por el cable de la figura circula una corriente I. Indicar la dirección del campo en cada uno de los puntos indicados, teniendo en cuenta que: a) El punto A está debajo del cable. b) El punto E está arriba del cable. c) Los puntos C y D están al mismo nivel que el cable. C A Vista desde Arriba E ORT 2013 I 4 D 8) Esquematizar el campo magnético generado en la espira cuando lo recorre una corriente como indica la figura: - + + Vista en Perspectiva Vista de Frente 9) Indicar los polos en cada uno de los electroimanes que se muestran a continuación: + 10) Según el esquema, ¿cuáles son los bornes positivo y negativo de la pila? 11) ¿Qué ocurrirá entre el electroimán y el imán cuando circule una corriente como la indicada por la flecha? N ORT 2013 S 5 12) En cada caso, ¿qué ocurrirá con los electroimanes cuando circule corriente? Justificar indicando los polos. Esquematizar el campo magnético generado por cada bobina. . + - + - - Caso A + - + - + Caso B - + - + Caso C + Caso D 13) En la espira de la figura la corriente entra por el extremo izquierdo y sale por el derecho. Esquematizar el campo magnético en los puntos indicados. A C E D 14) Se tienen 2 cables largos y paralelos por donde circula, por cada uno de ellos, una corriente de 10 A. Por uno de ellos la corriente sale y por el otro la corriente entra. a) Calcular y esquematizar el campo magnético total en los puntos A y C. b) Si se coloca una brújula en dichos puntos, ¿cómo se orientará? Esquematizar. Cable por donde circula una corriente entrante de 10 Amp A C 5cm ORT 2013 Cable por donde circula una corriente saliente de 10 Amp 8cm 8cm 6 15) Calcular el campo magnético en los puntos P, Q y S para cada configuración. 5A 5A 1A Q P 1A Q S P S d=8 cm d=15cm d d d d d d d d 0,2 A 0,2 A P d d d d d P Q d Q d d R 0,1 A d=2 cm 0,1 A R S S d=2 cm 16) En la región sombreada existe un campo magnético uniforme de intensidad B0 = 0,5 10-5 T, cuya dirección es hacia dentro de la hoja. Además hay un cable por el que circula una corriente de 0,2A. a) Calcular el campo magnético en un punto que se encuentra a 2 cm del cable sobre el lado izquierdo y a 2 cm del cable sobre el lado derecho. b) ¿En qué puntos el campo magnético será nulo? X X I X X X X B0 X X X X X X 17) Dentro de un imán en herradura se hace pasar un cable por donde circula una corriente saliente de 10 A., como indica la figura. Sabiendo que el campo magnético del imán es de 610-5Tesla se pide: a) Calcular y esquematizar el campo magnético en el punto A y en el punto C. b) Si se coloca una brújula en dichos puntos, ¿para dónde se orientará? Esquematizar. c) Contestar la pregunta anterior para el caso en que no circulara corriente por el cable. N C A 5cm S ORT 2013 Vista superior (desde arriba) 5cm Cable por donde circula una corriente saliente de 10 A. 7 Fuerza provocada al interactuar un campo con una corriente Supongamos que en un lugar determinado existe un campo magnético B (es indistinto para el análisis que sigue si este campo es producto de un imán permanente o de algún otro tipo de fenómeno de los discutidos). Si posteriormente se coloca un conductor por el que circula una corriente, la interacción entre el campo B que existía y la nueva corriente I provocará una fuerza F sobre las cargas (se manifestará en realidad como una fuerza sobre el conductor, a menos que las cargas estén libres viajando en el vacío). Esta fuerza se puede calcular como F lI B El símbolo (que en algunos casos también puede ser escrito como X) indica que la operación matemática a aplicar entre I y B es lo que se conoce como "producto vectorial". El producto vectorial es una operación que depende del ángulo entre los vectores. Si los vectores a los que se aplica el producto vectorial se encuentran a 90º entre sí, el cálculo se convierte en sólo una multiplicación. Cuando el ángulo entre los dos vectores es 0º (esto es, cuando son paralelos) entonces el resultado del producto vectorial es cero. En todos los otros casos el resultado será una parte (menor o a lo sumo igual) que la multiplicación entre los valores de los vectores. El modo preciso de cálculo expresa que F l I B sen( ) donde representa el ángulo entre el vector de la corriente I y del campo B. Así una corriente de 1 A que circula por un cable de 1 metro de longitud en presencia de un campo de 1 Tesla (que es inmenso) provocaría una fuerza de 1 Newton (unos cien gramos fuerza) como máximo, sólo cuando los vectores de I y B se encuentren perpendiculares. Por otra parte la fuerza de interacción sería igual a cero cuando los vectores se encuentren paralelos. En cualquier otra posición se obtendría algún valor entre 0 y 1 Newton. Es importante insistir en la diferencia con el caso analizado antes de un campo B generado por una corriente I, ya que ahora en este nuevo cálculo el campo B preexiste a la corriente I. Ese campo B puede haber sido generado por un imán permanente o por otra corriente que no está teniéndose en cuenta en forma directa. Siempre aparece una situación de confusión cuando uno piensa en este problema ya que suele razonar diciendo algo así: "Hay un campo B1 provocado por causas externas a la corriente I2 que se establece en un conductor, pero una vez establecida la corriente I2 ésta generará un campo B2 que se agregará al que existía antes. El campo total existente ahora será diferente al B1 que había y por lo tanto debería obtener el nuevo campo Btotal antes de calcular la fuerza". Pues bien, este modo de razonar no es el que se busca. La ecuación fue obtenida en base al valor del campo B1 (y no de Btotal). El producto vectorial da por resultado un vector y además define la dirección y sentido de este vector resultante. El sentido de la fuerza F puede obtenerse aplicando una nueva regla de la mano derecha (con ligeras modificaciones sobre la anterior). Recordemos que en el caso anterior el pulgar representaba la corriente y los dedos el campo generado. Si se extienden los dedos para representar el campo externo la palma indicará el sentido de la fuerza. ORT 2013 8 18) En los siguientes casos se muestra un imán y un cable recto por donde circula una corriente eléctrica hacia afuera de la hoja y perpendicular a ella. Esquematizar en cada uno de ellos la fuerza que actúa sobre el cable. a) c) b) N S S d) N N S S N 19) ¿Para qué lado se moverá el péndulo? 20) Sabiendo que la barra del péndulo tiene un largo de 10cm y una resistencia eléctrica de 0,5 y ésta se conecta a una fuente de 12 V como se muestra en la figura. Se pide: a) Calcular la corriente que circula por el circuito. b) Calcular la fuerza sobre la barra, si el campo magnético generado por el imán es de 10-5 T. Dibujarla sobre el dibujo. Esquema del circuito =12V =12V RBARRA= 0,5 21) Indicar la magnitud y la orientación de la fuerza magnética que se ejerce sobre un cable de 10cm de largo sabiendo que el campo magnético que existe entre los polos del imán es de 10-5 T. I=1A N S 22) Indicar la magnitud y la orientación de la fuerza magnética que se ejerce sobre un cable de 1m de largo sabiendo que el campo magnético que existe entre los polos del imán es de 210-5 T. S I=1A N ORT 2013 9 23) Indicar la magnitud y la orientación de la fuerza magnética que se ejerce sobre el cable de 1m de largo sabiendo que el campo magnético es de 210-5 T. En este esquema el dibujo está representado como si se observara desde una cámara ubicada en el norte y apuntando hacia el sur del imán, por lo que el campo magnético será entrante. I=1A B = 210-5 T 24) Se tienen dos cables (cable 1 y cable 2) paralelos de 1m de largo cada uno a una distancia de 40cm. Por el cable 1 circula una corriente entrante de 10A. y por el cable 2 una saliente de 30A. Se pide: a) Calcular y esquematizar el campo en el cable 2 generado 40cm por la corriente I1 (indicarlo con un vector). I1 I2 b) Calcular y esquematizar el campo en el cable 1 generado por la corriente I2 (indicarlo con un vector). c) Si en el cable 1 hay corriente y hay un campo, se puede Corriente entrante Corriente saliente calcular y esquematizar la fuerza aplicada sobre el mismo. Hacerlo. d) Si en el cable 2 hay corriente y hay un campo, se puede calcular y esquematizar la fuerza aplicada sobre el mismo. Hacerlo. e) ¿Los cables se atraerán o se rechazarán? 25) Un conductor MN de masa igual a 0,6 kg. está apoyado sobre dos rieles conductores horizontales, a través de los cuales circula una corriente de 40A mediante un generador conectado a los puntos L y Q. Además, hay un campo magnético uniforme B de 0,26 T en un plano perpendicular a los rieles. La distancia entre los rieles es de 0,5 metros y la fuerza de rozamiento entre el conductor y los rieles es de 4 Newton. Calcular la fuerza total que actúa sobre el conductor y la aceleración que este adquiere. N B Q i L M 26) El dispositivo de la figura es conductor, está ubicado en un plano vertical y sumergido en un campo magnético uniforme cuyas líneas son normales a dicho plano y están dirigidas hacia adentro. Mediante un generador conectado a L y Q se mantiene una corriente de 20A. El trozo MN puede deslizarse con rozamiento despreciable y tiene una longitud de 0,4 metros. a) Esquematizar las fuerzas que actúan sobre el cable. b) Calcular cuánto pesa ese trozo sabiendo que está en reposo y que el valor del campo magnético es de 0,09 Tesla. B M L ORT 2013 i N Q 10 27) ¿Cuál es el valor del campo magnético que se origina en el centro de una espira circular de 55 centímetros de radio por la que circula una corriente de 18A? 28) ¿Cuál es el valor del campo magnético que se origina en el centro de una bobina circular plana de 150 espiras y de 83 centímetros de radio por la que circula una corriente de 15A? 29) ¿Cuál es el radio de una espira circular sabiendo que cuando por ella circula una corriente de 9A, se origina en su centro un campo magnético de 5,2.10-5 Tesla? 30) Una bobina circular, de 15cm de radio, constituida por 30 espiras se coloca en un plano vertical, en el meridiano magnético donde la componente horizontal del campo de la Tierra es de 2,510-5. En el centro de ella se coloca una brújula. a) Calcular el ángulo que se desviará la brújula al circular por la bobina una corriente de 2A. b) Dibujar los vectores a escala (el del campo Terrestre y el del campo producido por la bobina). 31) El escritor colombiano Gabriel García Márquez, recibió el Premio Nobel de Literatura en el año 1982. En su libro Cien años de soledad se narra la historia de una familia y de un pueblo en un imaginario país tropical. El libro fue publicado por primera vez en nuestro país en el año 1967 y marcó un estilo particular en la literatura latinoamericana. De las primeras páginas de esta novela tomamos estos fragmentos: “El mundo era tan reciente que muchas cosas carecían de nombre, y para mencionarlas había que señalarlas con el dedo. Todos los años, por el mes de marzo, una familia de gitanos desarrapados plantaba su carpa cerca de la aldea, y con un gran alboroto de pitos y timbales daban a conocer los nuevos inventos. Primero llevaron el imán. Un gitano corpulento, de barba montaraz y manos de gorrión, que se presentó con el nombre de Melquíades, hizo una truculenta demostración pública de lo que él mismo llamaba la octava maravilla de los sabios alquimistas de Macedonia. Fue de casa en casa arrastrando dos lingotes metálicos, y todo el mundo se espantó al ver que los calderos, las pailas, las tenazas y los anafes se caían de su sitio, y las maderas crujían por la desesperación de los clavos y los tornillos tratando de desenclavarse, y aún los objetos perdidos desde hacía mucho tiempo aparecían por donde más se les había buscado, y se arrastraban en desbandada turbulenta detrás de los fierros mágicos de Melquíades. «Las cosas tienen vida propia —pregonaba el gitano con áspero acento—, todo es cuestión de despertarles el ánima». José Arcadio Buendía, cuya desaforada imaginación iba siempre más lejos que el ingenio de la naturaleza, y aun más allá del milagro y la magia, pensó que era posible servirse de aquella invención inútil para desentrañar el oro de la tierra. Melquíades, que era un hombre honrado, le previno: «Para eso no sirve». Pero José Arcadio Buendía no creía en aquel tiempo en la honradez de los gitanos, así que cambió su mulo y una partida de chivos por los dos lingotes imantados.” “...Durante varios meses se empeñó en demostrar el acierto de sus conjeturas. Exploró palmo a palmo la región, inclusive el fondo del río, arrastrando los dos lingotes de hierro y recitando en voz alta el conjuro de Melquíades.” a) Investiguen el significado de los términos que no conozcan. b) ¿Qué resultado les parece que dio la exploración de José Arcadio Buendía? ¿Por qué? c) Al sumergirlos en el río ¿los lingotes metálicos de Melquíades perderían su efecto? Justifiquen su respuesta. Sugerencia: En algún momento leer el libro. Realmente vale la pena. ORT 2013 11 Respuestas y Ayudas 2) es similar al 3) La dirección de la brújula indica la dirección del campo 4) Si colocás ambas barras formando una “T”, lo resolverás 11) Se repelen. 12) Caso A: Se Rechazan Caso B: Se Atraen Caso C: Se Atraen Caso D: Se Rechazan 14) BA=3,0510-5T hacia arriba BC=510-5T hacia abajo 15) BQ=7,110-6T Saliente ☉ BP=5,3310-6T Entrante BS=3,510-6T Entrante BP=310-6T Saliente ☉ BQ=110-6T Saliente ☉ BR=210-6T Saliente ☉ BS=0 BQ=1,1610-5T Saliente☉ BP=1,510-5T Entrante BS=1,610-6T Entrante BP=310-6T Entrante BQ=110-6T Entrante BR=210-6T Entrante BS=0 16)a) BIZQUIERDA=310-6T Entrante BDERECHA=710-6T Entrante b) 0,8 cm=0,008m 17)a) BA=110-4T hacia abajo BC=7,210-5T 56º b) La dirección del campo será la dirección a la cual se orienten las brújulas. c) El campo producido por el imán va de Norte a Sur, es decir, hacia abajo, y esa será la dirección de las brújulas. 18) 19) 20) 21) 22) 23) 24) a)Hacia arriba b)Hacia abajo c)Hacia la derecha d)Hacia la izquierda Hacia la derecha a)I=24A b) F=2,410-5N F=110-6N Saliente ☉ F=210-5N Entrante FMAGN=4,510-4N FMAGN=4,510-4N F=210-5N Hacia abajo Mirá el esquema con los campos sobre cada cable y las B2=1,510-5N fuerzas. Notá que no es casualidad que las fuerzas sobre cada B1=510-6N cable den igual, esto es una muestra más del principio de acción y reacción. Loa cables se rechazarán ☉ B 25) FTOT=1,2 N hacia la derecha Se moverá con a=2m/s 26) B 2 FMAGN=5,2N FROZ=4N FMAGN=0,72N I P=0,72N 27) B=2,0510-5T 28) B=1,710-3T 29) 10,8cm=0,108m ORT 2013 12 30) Esquema fuera de escala BTierra 5º BTot=2,510-4T BBobina ORT 2013 13