Problema 6.35
Anuncio

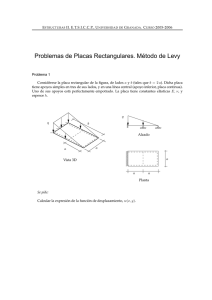
MECÀNICA DE FLUIDS – ENG. AERONÀUTICA Sesions de problemes, curs 2010/2011- quatrimetre 2 Grup: 3.2 Components: Víctor Ferrer-Dalmau Font Jordi García Marçal Fernández PROBLEMA 6.35 En la Figura1 se presenta el esquema que pretende hacer el estudio de las pequeñas “aletas” que a veces se colocan sobre la superficie de un perfil aerodinámico. El modelo propuesto a estudio son dos placas planas delgadas lisas, una en posición horizontal respecto al flujo no perturbado y otra en posición vertical, formando un ángulo de 90º con la placa horizontal, tal como se muestra en la Figura 1. Un flujo de aire de velocidad constante U=40m/s incide sobre la placa horizontal y sus propiedades físicas se pueden considerar constantes (1.2kg/m3 y 1.5·10-5m2/s). Se pide para diseñar y dimensionar la placa plana vertical: a. Calcular la fuerza de arrastre que se produce en la placa plana horizontal debido únicamente a la capa límite laminar. Desde el borde de ataque a Xlam. Tener en cuenta las dos caras de la placa y que el ancho de la placa plana horizontal es de b=220mm. b. Calcular la distancia Xini a la que se debe situar el inicio de la placa plana vertical de forma que esta distancia sea 20 veces la distancia Xlam de la capa límite laminar formada en la placa plana horizontal Xini=20·Xlam. c. Calcular la altura H de la placa plana vertical en el punto Xini que corresponde al espesor de la capa límite turbulenta. d. Supongamos ahora que a partir del punto Xini la capa límite turbulenta sobre la placa plana horizontal no evoluciona más, de forma que su perfil de velocidades cumple un perfil exponencial del tipo donde δ≡H se mantiene constante a partir de Xini. Además, supongamos que la capa límite en toda la placa plana vertical es turbulenta. Entonces, calcular la longitud B de la placa plana vertical para que la fuerza de arrastre producida en ella sea la misma que la obtenida en el apartado a). tener en cuenta las dos caras de la placa. e. Calcula el coeficiente de arrastre de la placa plana vertical. Nota importante: Dibujar el esquema/dibujo correspondiente en cada apartado que represente los cálculos realizados. Hipótesis • • • • • • Fluido newtoniano (aire) Proceso estacionario Flujo incompresible Flujo unidimensional y uniforme Suponemos efectos de capa límite No tenemos en cuenta gradientes de presión Esquema U Resolución a. Para calcular la fuerza que se produce en la placa plana horizontal utilizaremos las ecuaciones de Blasius. El parámetro b es el ancho de la placa: CD = = . √ (1) Al tratarse de una placa plana y capa límite laminar tenemos que imponer que el número de Reynolds sea menor o igual que 10! . De tal manera: Rex = " ≤ 10! (2) Resolviendo la ecuación (2) obtenemos el valor de Xlam ≤ 0.375. Una vez se conoce este valor se substituye en la ecuación (1) y resolvemos para FD. Obtenemos un valor de la fuerza igual a 0.21N (teniendo en cuenta las dos caras de la placa plana horizontal). FD = 2 . √ $ % &'() = 0.21 N b. Hacemos caso del enunciado y multiplicamos Xlam por 20: Xini = 20·Xlam = 7.5m Este resultado parece erróneo, pues es desproporcional a las magnitudes del problema. En realidad este problema estaba pensado para que en vez de aire fuese agua el fluido, por lo que sus constantes eran distintas y esta longitud no salía tan grande. c. Como ahora ya hemos pasado la distancia donde el flujo cambia a turbulento, ya no podemos seguir trabajando con las ecuaciones de Blasius. En su lugar utilizaremos las fórmulas de capa límite turbulenta. Partimos de la ecuación que nos relaciona el espesor de la capa límite con el número de Reynolds: δ= *.! (3) y Rex= " (4) Donde X es la distancia Xini. Operando con la expresión (4) obtenemos Rex1/7=10.96. Introduciendo dicho valor en la expresión (3) nos sale un valor de: δ = 0.104m d. En este apartado seguimos trabajando con capa límite turbulenta, por lo que seguimos sin poder utilizar Blasius. El estudio se basa en la aleta vertical, de tal manera que la velocidad del flujo incidente ya no es la velocidad del flujo exterior, sino que está perturbada por los efectos de la capa límite. Por ello las ecuaciones utilizadas en este apartado se deben tratar de modo diferencial. Flujo incidente V(y) y x dy H B Esta es la placa plana vertical vista de cara. Como el flujo incidente solo depende de y deberemos integrar la expresión de la fuerza respecto de dicha variable. Utilizando la misma formulación que en el apartado anterior escribimos FD en función del CD. +, 2+, 1 $ - . /, 01 2 $ . /, 01 21 En este caso CD también es función de ‘y’: /, (5) *.* (6) 345 6 Introducimos (6) en (5) y simplificamos las constantes. +, 9 $ 0.031 √8 . ; < :* 0 1 21 (7) Substituyendo en (7) el perfil de velocidades dado: +, 9 ; 9 ; $ 0.031 √8 . < ; :* => 21 (8) Recordar: δ≡H. Integrando la ecuación (8): +, ?@ $ 0.031 √8 . AB CD ! < * Como el efecto de la capa límite se experimenta por igual en los dos lados de la placa vertical debemos tener en cuenta que la fuerza resultante en una cara es la mitad del valor obtenido en el apartado a. De tal manera igualamos el valor de la fuerza a 0.105 N (pues solo nos interesa la fuerza que ejerce una cara para obtener la dimensión de B). Resolviendo para encontrar B sale un resultado de aproximadamente 0.29m e. Llegados a este punto, lo único que debemos hacer para acabar es utilizar la definición de CD. Introduciendo todos los parámetros conocidos llegamos al valor de dicho coeficiente. /, FD= 0.105 N (una sola cara) CD=0.16 +, 1 2$.-