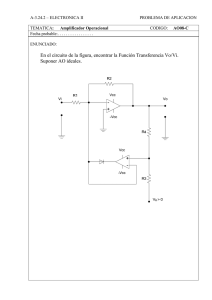
i v R =

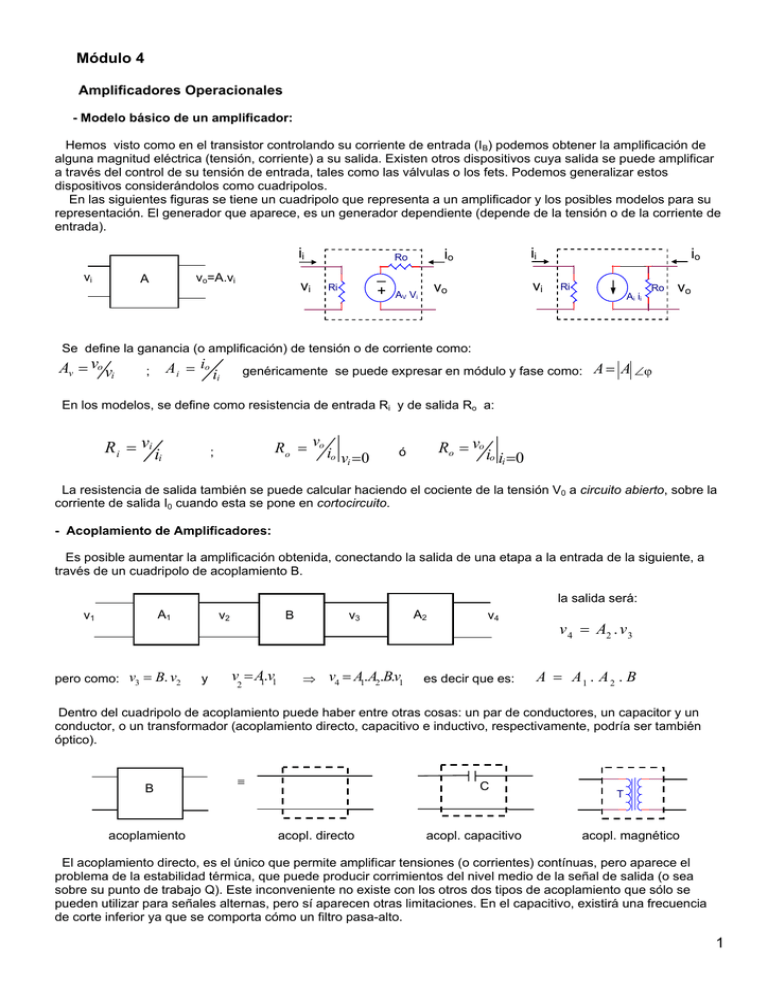
Módulo 4
Amplificadores Operacionales
- Modelo básico de un amplificador:
Hemos visto como en el transistor controlando su corriente de entrada (IB) podemos obtener la amplificación de
alguna magnitud eléctrica (tensión, corriente) a su salida. Existen otros dispositivos cuya salida se puede amplificar
a través del control de su tensión de entrada, tales como las válvulas o los fets. Podemos generalizar estos
dispositivos considerándolos como cuadripolos.
En las siguientes figuras se tiene un cuadripolo que representa a un amplificador y los posibles modelos para su
representación. El generador que aparece, es un generador dependiente (depende de la tensión o de la corriente de
entrada).
ii
vi
vo=A.vi
A
vi
_
+
Ri
ii
io
Ro
vi
vo
AV Vi
io
Ri
Ai i i
Ro
vo
Se define la ganancia (o amplificación) de tensión o de corriente como:
Av = vo vi
A i = io i
i
;
genéricamente se puede expresar en módulo y fase como:
A = A ∠ϕ
En los modelos, se define como resistencia de entrada Ri y de salida Ro a:
R i = vi i
Ro = vo io
vi =0
;
i
Ro = vo i
ó
i =0
o i
La resistencia de salida también se puede calcular haciendo el cociente de la tensión V0 a circuito abierto, sobre la
corriente de salida I0 cuando esta se pone en cortocircuito.
- Acoplamiento de Amplificadores:
Es posible aumentar la amplificación obtenida, conectando la salida de una etapa a la entrada de la siguiente, a
través de un cuadripolo de acoplamiento B.
la salida será:
A1
v1
pero como: v3 = B. v2
v2
y
B
v = A1.v1
2
v3
⇒
v4 = A1.A2.B.v1
A2
v4
es decir que es:
v 4 = A2 . v 3
A = A1 . A 2 . B
Dentro del cuadripolo de acoplamiento puede haber entre otras cosas: un par de conductores, un capacitor y un
conductor, o un transformador (acoplamiento directo, capacitivo e inductivo, respectivamente, podría ser también
óptico).
B
acoplamiento
≡
C
acopl. directo
acopl. capacitivo
T
acopl. magnético
El acoplamiento directo, es el único que permite amplificar tensiones (o corrientes) contínuas, pero aparece el
problema de la estabilidad térmica, que puede producir corrimientos del nivel medio de la señal de salida (o sea
sobre su punto de trabajo Q). Este inconveniente no existe con los otros dos tipos de acoplamiento que sólo se
pueden utilizar para señales alternas, pero sí aparecen otras limitaciones. En el capacitivo, existirá una frecuencia
de corte inferior ya que se comporta cómo un filtro pasa-alto.
1
En el caso del inductivo, se tienen dos frecuencias de corte, debidas al comportamiento como pasa-banda del
transformador que no responde a frecuencias muy bajas y muy altas.
Una de las ventajas de los amplificadores de acoplamiento directo, es que no introducen una frecuencia de corte
inferior. En la práctica tienen una frecuencia de corte superior, debida a la resistencia de salida y las capacidades
parásitas inevitables, que existen en cualquier dispositivo o circuito.
- Amplificadores operacionales:
Para reducir los problemas indicados, se han desarrollado los amplificadores operacionales. Su símbolo y su
ecuación de salida son:
Vcc+
v1
vi
v2
-A
O
vO = AO vi = AO (v2 - v1)
+
Vcc
(*)
-
v1 y v2 son las entradas que necesariamente tienen que estar referidas a la masa común de Vcc+ y Vcc
-
que son las alimentaciones de tensión que necesita el operacional para que trabajen adecuadamente sus circuitos
internos, formados por transistores, diodos, resistencias, etc...
nota:
La ecuación de la salida (*) no tiene en cuenta el echo de que v0 nunca puede tomar un valor mayor al de las
alimentaciones Vcc+ y Vcc .
-
Amplificador operacional ideal:
Veamos ahora cuales son las características principales de un amplificador operacional ideal:
1234-
Amplifica la diferencia de las tensiones de sus dos entradas (v2 - v1) con ganancia infinita, AO =∞.
Cuando vi = v2 - v1 = 0, la tensión de salida es cero. (offset nulo).
La nulidad del offset es independiente de la temperatura (drift nulo).
No amplifica la tensión de modo común de sus dos entradas (v2 + v1)/2
(CMRR=∞: Relación de Rechazo de Modo Común ).
5- No toma corriente por sus entradas.
6- La resistencia de entrada Ri es infinita.
7- La resistencia de salida Ro es cero.
8- El ancho de banda es infinito , fT=∞.
-
Funcionamiento: Normalmente se alimentan con 2 fuentes (Vcc+ y Vcc ), para que la tensión de salida pueda llegar a
ser cero. En su diseño se ha cuidado también de que la temperatura tenga un efecto mínimo sobre la salida.
Tienen dos entradas, identificadas con los signos “+” y” –“, que se denominan respectivamente "no-inversora" e
"inversora" y una sola salida. El nombre de las entradas viene de que si se entra con una señal por el terminal "+",
a la salida se obtiene una señal sin inversión de fase. Si se ingresa por el terminal "-" a la salida se tiene una señal
con una inversión de fase de 180º (siempre con referencia a la masa o común de la señal).
En la gran mayoría de las aplicaciones no se utilizan los amplificadores operacionales (Op-Amp) con toda la
ganancia que pueden suministrar. Se acostumbra tomar una parte de la señal de salida, para oponerla a la de
entrada (realimentación negativa). Veamos como ejemplo el amplificador no-inversor.
- Amplificador no-inversor:
El siguiente es el esquema de un amplificador que utiliza un Amplif. Operac. Por simplicidad del dibujo se han
omitido las alimentaciones Vcc+ y Vcc . Calculemos la ganancia de tensión AV .
R2
I1
-
+
Vs
-
R1
+
Vi
ii
+
I2
Av = vo vs
-
y como: I1= I2 ;
A0
+
fig.1
donde :
v s = ( v i + v R1 )
v R 1 = vo R1 ( R + R )
1
2
Vo
2
vo = vi A0
Av =
⇒
1
Si se cumple que:
R1
A 0 ⟨⟨
v i A0
[ v i + v i A0 R 1 ]
( R1 + R 2 )
( R1 + R 2 )
(*)
Av =
1
1
[ A + ( R R+1R ) ]
0
1
2
A v ≅ [1 + ( R 2 R ) ]
1
⇒
Se observa que la amplificación prácticamente queda definida por una relación resistiva y que no intervienen
otros parámetros del amplificador.
Se hubiese llegado al mismo resultado, despreciando a v i frente a vR1 [ se ve en (*)], quedaría
Podemos afirmar que el resultado anterior es consecuencia de los siguientes puntos:
v s ≅ v R1 .
1- La gran ganancia Ao del amplificador operacional
2- La gran impedancia de entrada del mismo que hace que su corriente de entrada ii ≈ 0
3- La realimentación negativa (⇒ de la salida al terminal inversor)
Estos factores me permiten suponer, en todos los casos que se use un amplificador operacional
“con realimentación negativa” se cumplirá que Vi=0 ( V+ = V ).
-
Realimentación positiva y negativa:
-
El análisis anterior se podría haber hecho intercambiando las entradas V+ = V . En este caso la única diferencia
R
sería que en la ecuación de la ganancia de tensión habría un cambio de signo: A v ≅ − [1 + ( 2 R ) ]
1
Sin embargo el cambio es mucho mas importante porque la realimentación pasaría ser de negativa a positiva.
Veamos prácticamente cuál sería la diferencia entre ambos casos.
- Realimentación negativa:
Supongamos que en el circuito anterior por algún motivo (por ej. un cambio de temperatura ambiente) aumenta
levemente el valor de la salida Vo. Esto implicaría un aumento de la tensión en la entrada inversora ( V ) con lo que
+
disminuiría la diferencia (V - V = vi ) y por lo tanto Vo = vi .Ao. O sea que se vería corregido el aumento de la salida.
- Realimentación positiva:
Ahora vayamos al caso donde en el circuito anterior se intercambian V+ y V . Ante similar aumento de la salida
se producirá ahora un aumento (V+ - V ) con lo que se acentuará el aumento de la salida y se repetirá el efecto sobre
la entrada y así sucesivamente con lo que la salida rápidamente irá a su máximo valor posible que es Vcc+ . O sea
que con realimentación positiva se logra potenciar aun mas la variación de la salida ⇒ en lugar de corregir, acentúa.
Análisis simplificado de un circuito con amplificador operacional y realimentación negativa:
Teniendo en cuenta lo dicho podemos hacer el análisis del circuito anterior de la siguiente forma:
si Vi=0 ⇒ V+ = V = Vs ∴ la tensión sobre R1 es: VR1=Vs ⇒ I1=Vs / R1
Cómo el operacional no toma corriente tendremos : I1 = I2 ⇒ VR2 = I1 .R2
por otro lado tenemos que la salida V0 = VR2 + VR1
∴ V0 = I1 R2 + I1 R1 = I1 (R1 + R2 )
V0 = Vs (R1 + R2 ) / R1
⇒
pero como I1 = Vs / R1 tendremos que:
AV =V0 / VS = (1 + R2/R1 )
coincidente con el resultado anterior.
- Resistencia de entrada Ri del no-inversor:
ii
vs
Ro
Ri
_
+
Av Vs
io
vo
Si suponemos el circuito no-inversor como un cuadripolo
tendremos que su resistencia de entrada Ri vale
Ri = vs / ii y como para esta configuración ii=0 tendremos:
Ri = ∞
3
-Seguidor (ó buffer):
Si en el circuito del no-inversor se hace: R1=∞ ó R2=0 , o se cumplen ambas simultáneamente, la amplificación
resulta seriía Av =1, es decir que la señal de salida es igual a la de entrada. A éste circuito se lo denomina seguidor
+
Vo=Vs
Vs
Tiene la ventaja de una muy alta resistencia de entrada y una baja
resistencia de salida. Se utiliza para adaptar impedancias por ej.
entre dos filtros o para no “cargar” una fuente.
El operacional real:
Veamos las características de dos amplificadores operacionales reales como ser el CA3140 y el OP07 cuyas
especificaciones típicas @ Vcc+=+15V ; Vcc- =-15V y Tamb = 25 oC son:
CA3140
OP07
1- Ganancia a lazo abierto finita AO
100.000
500.000
2- tensión de offset
5mV
30µV
3- drift
8µV/°C
0.3µV/°C
4- CMRR
90dB
126dB
5- Corriente de entrada
10pA
1nA
6- Ri
1.5 TΩ (1.5x1012Ω)
200GΩ
60Ω
60Ω
7- Ro
8- Ancho de banda fT
4,5Mhz
0,6Mhz
nota:
Un punto muy importante a tener en cuenta cuando se usan los datos de los manuales, son las tensiones de
alimentación (Vcc+ ; Vcc-) y la temperatura ambiente (Tamb) para los que estos se especifican. Además no hay que
olvidar los Maximum Ratings que nunca deben ser sobrepasados para no destruir el dispositivo.
- Tensión de off-set vOff :
vOff es una tensión, de polaridad no definida, que aparece en los bornes de entrada del operacional debido a
defectos en la construcción del mismo. Se puede simular con el siguiente modelo:
Vcc+
voff
v1
Vemos que esta tensión voff se suma a (v2 – v1) y es amplificada:
-
vO =Ao vi = Ao (voff + v2 - v1)
vi Ao
+
v2
vO
Vcc−
si : v2 - v1 = 0 ⇒ vO = Ao .voff
Sí en el circuito no-inversor consideramos la vOff y aplicamos superposición (cortocircuitando Vs) tendremos:
como V+ = V = 0V ⇒ vOff queda aplicado sobre R1 haciendo circular una corriente IOff=VOff/R1 la que también
R2
circulará por R2, produciendo a la salida:
Ioff
voff
Vo’ = voff (1+ R2/R1)
R1
2
Esta Vo’ se sumará a la tensión Vo” producida por Vs:
+
Vo” = VS (1+ R2/R1)
∴
Vs
3
+
6
Vo=(Vs+voff) (1+ R2 /R1 )
-
V0 = Vo’ + Vo” = ( Vs+voff) (1+ R2 /R1 )
Vemos que si la señal a amplificar es muy pequeña, por ej. la de una termocupla (40µV/°C) entonces el off-set
( 5mV para el CA3140) tapará a la señal útil.
Luego cuando voff es comparable a la tensión de la señal a amplificar, debe ser corregido ó seleccionar un
Op Amp. que tenga baja voff , por ejemplo el OP07 ú OP77 (voff=25µV).
Vcc+
Para esto el Op-Amp cuenta con dos terminales (1 y 5 en el CA3140) a los que se les
conecta un potenciómetro cuyo punto medio está a la alimentación negativa del operacional
Vcc- . De esta manera se crea una tensión opuesta a la de off-set anulando su influencia.
+
5
1
Vcc-
4
- Drift:
Cuando nos referimos al drift (corrimiento) estamos hablando del térmico. Generalmente de la variación del off-set
con la temperatura ( 8µV/ºC p/ el CA3140). Es un dato importante ya que podemos corregir el off-set pero esto será
insuficiente si después cambia la temperatura del operacional ya sea porque varió la Tamb o porque varía el
calentamiento propio al variar la corriente de salida.
- Rechazo de Modo Común CMRR:
Internamente el Op. Amp. es un amplificador diferencial, quiere decir que amplifica solamente la diferencia de
tensiones entre sus terminales de entrada v1 y v2 referidas a masa. La señal de salida de un amplificador diferencial
ideal es: vo = Ad (v2 - v1) = Ad.vd, siendo Ad su ganancia, que coincide con la Ao vista, del Amplif. Operacional ideal.
Si v1 y v2 fueran tales que existiera un valor medio común vc =(v1+v2)/2 , el diferencial ideal no amplificaría dicha vc;
cosa que si ocurre en el diferencial real. El modelo para este caso sería el siguiente:
v1
vd/2
vd = v2 – v1
vd/2
Ad ; Ac
vc = (v2 + v1) / 2
vd/2
+
vo= Ad vd + Ac vc
v1 vc v2
vc
v2
Luego, un Amplificador Operacional real no puede representarse por la ecuación vo = Ao (v2 - v1), ya que la
salida depende no sólo de la señal diferencia: vd =v2 - v1 sino también de su nivel medio, llamada señal de
modo común: vc=(v2 + v1) / 2 la cual es amplificada con una ganancia de modo común Ac, que suele ser
mucho menor a Ad. De esta manera tenemos que la salida real responde a la ecuación:
vo = Ad vd + Ac vc
O sea que no es lo mismo amplificar señales dónde v2 =+ 50µV y v1 = - 50µV (vd=100µV; vc =0V), que otras dónde
v2 =+ 1050µV y v1 =+ 950µV ; tendremos la misma vd=100µV pero vc= (1050+950)µV/2 = 1000µV.
A la relación entre las dos ganancias: Ad/Ac se la denomina Rechazo de Modo Común (CMRR) y es un dato de los
Amplificadores Operacionales, que suele venir expresado en decibeles dB:
CMRR [dB] = 20 log Ad / Ac
Generalmente es una relación alta, p/ el CA3140 es de 90 dB . O sea que la ganancia diferencial Ad es apróxim.
32.000 veces superior a la ganancia de modo común Ac. Para el OP0/ es de 126dB, o sea Ad / Ac=1.995.262
Al final del módulo 4 hay un apéndice donde se ve la influencia de la señal de modo común en un amplificador
inversor y no-inversor.
Los Max. Ratings dan valores límites de vd y vc. P/el CA3140 son: vdmáx=+/- 8V ; vcmáx=Vcc+ + 8V y Vcc- - 0,5V
- Ancho de Banda fT :
El Op-Amp tiene una frecuencia superior de corte (pasa-bajo) dada por sus capacidades parásitas internas.
El parámetro que la especifica es fT denominado “Producto Ganancia-Ancho de Banda”. O sea que sería el ancho
de banda para una ganancia de 1. Su valor va desde 0,5Mhz a 300Mhz dependiendo del tipo de operacional.
fT es una constante, implica que si aumentamos la ganancia, el ancho de banda disminuirá.
Para el CA3140: fT=4,7Mhz o sea que si lo trabajara sin realimentación, donde su ganancia es de 100.000 su
ancho de banda se reduciría a 47hz.
Si lo uso en una configuración no-inversora como la vista, con una ganancia : Av = (1+R2/R1) =10 entonces el
ancho de banda se reducirá a 470Khz. Ejemplo: supongamos que necesitamos amplificar por 100 una determinada
señal de 100 Khz con un Op-Amp de fT = 5Mhz.
El ancho de banda se reducirá a fT/100=50Khz con lo que la señal de entrada no será amplificada por 100. Se
podría pensar en usar dos amplificadores uno detrás del otro -c/u de ganancia 10- con lo que la ganancia final
seguiría siendo de 100. ¿Qué sucede con el ancho de banda total?
vi
A1=10
fc1=500khz
A2=10
fc2=500khz
vo=vi.A1.A2 =100vi
Ahora el ancho de banda de cada amplificador por separado será: fT = 500Khz sin embargo el ancho de banda total
no es de 500Khz!!
5
Debemos pensar a cada amplificador como si fuera un filtro pasa-bajos. Recordemos que si usábamos dos pasabajos en cascada, con la misma frecuencia de corte (separados por un buffer) y hacíamos el Bode resultante,
encontrábamos que la frecuencia de corte resultante no era la que tenía cada uno de los filtros por separado sino
que esta disminuía. Lo mismo sucede con los amplificadores.
Se pude demostrar que cuando las frecuencias de corte son iguales y de valor fC el ancho de banda
f R = fC
resultante fR será:
n
2 −1
con “n” igual a la cantidad de amplificadores en cascada
∴ para dos etapas tendremos fR = 0,643 fC. Para el ejemplo dado es: fR=0,643 . 500Khz = 321Khz
∴ podemos amplificar nuestra señal mejor que antes [lo ideal sería que la frecuencia de corte fR, esté al menos una
década por arriba (fR=1Mhz) de la frec. de nuestra señal (100Khz)].
- Corriente de salida iO :
Otra de las limitaciones de los amplificadores operacionales es la capacidad de entregar corriente ( iOM+ = Isource) y
de tomar corriente ( iOM- = Isink) en su salida (terminal 6).
En un CA3140 cuando está alimentado con Vcc+ = 5V y Vcc- =0V se tiene : Isource=10mA e Isink=1mA
En el circuito vemos que:
iO = I2 + IL
I2≡I1
R2
O sea que el operacional tiene que poder suministrar tanto la
corriente de la realimentación (I2) cómo la de la carga (IL).
Si se le pide más de lo que puede entregar se corre el riesgo
de dañarlo, de todas formas dejará de trabajar correctamente.
I1
R1
+
Vs
-
2
-
3
+
io
IL
+
6
ii
VO≡VL RL
Tenemos entonces dos limitaciones importantes en su salida:
-
- Máxima tensión de salida Vcc- < vo < Vcc+
- Maxima corriente que puede suministrar (source) y tomar (sink).
-
Amplificador Inversor:
Si en el esquema del no-inversor, se conecta la entrada no-inversora a masa y se entra con la señal por R1 , se
obtiene un amplificador inversor.
I2
R2
ii ≡ I1
+
Vs
-
+
+ R1 Vi=0
2
3
+
6
-
Vo = Vs ( - R2 / R1)
Nuevamente debido a las características del Op-Amp y a la realimentación negativa se cumple v i ≡0 con lo que en
este caso la entrada inversora del operacional tiene la tensión de masa, se dice que es una "masa o cero virtual".
Como se supone que no entra corriente al mismo la corriente I1 que circula por R1, debe ser la misma que por R2.
Ya que la entrada inversora es un cero virtual tendremos que:
Vo = -I2 R2
∴
Av ≅ − R2 R
1
además:
I2=I1 =Vs/R1
⇒
Vo = -Vs .R2 / R1
⇒ la amplificación queda definida por una relación resistiva.
Si : R2 = R1 ⇒ Av ≅ − 1 , es decir que sólo se obtiene una inversión de la señal de entrada sin afectar su amplitud.
En el inversor también se da que la tensión de off-set VOff , se amplifica por la ganancia 1+ R2/R1.
nota:
En esta configuración las entradas v+ y v- están a masa, con lo que su tensión a modo común vc es cero.
Cosa que no sucede en la configuración no-inversora donde ambos terminales están a vs que pasa a ser también vc.
Por lo tanto cundo se use la no-inversora, en mediciones de precisión, hay que tener en cuenta el CMRR para no
introducir errores a la salida, debidos a la tensión de modo común (vc).
6
- Resistencia de entrada del inversor:
Como en todo cuadripolo la resistencia de entrada es:
Ri = vi / ii
en este caso vi≡Vs y ii=I1 ; además I1=Vs / R1 con lo cual tendremos que:
R i = R1
nota: Ri ya no es infinita como en el no-inversor. Es importante tener en cuenta esto ya que la ganancia Av = - R2/R1
la puedo lograr con distintos pares de resistencias, siempre que mantengan la relación entre ellas. Se debe elegir
entonces una R1 tal que no me cargue al generador de entrada Vs. O sea que R1 sea mucho mayor que Rs
(resistencia interna del generador). También hay que tener en cuenta que I1 me la debe suministrar el operacional
(iO=I1+IL) e I1=Vs/R1 este es otro motivo por el que hay que prestar atención a la elección de R1.
- Conversor corriente-tensión:
Si en la configuración inversora se hace R1=0 se tiene la posibilidad de transformar la corriente “i” que entra al
"cero virtual" en una tensión, a la salida del operacional.
+
R
Como amperímetro es ideal ya que la resistencia equivalente de
entrada es:
i
-
i
Ri= Vi / ii
-
Vi=0
+
y como
V i≈ 0
⇒
Ri ≈ 0
Vo = - i.R
Esta configuración se usa por ejemplo, para medir la corriente inversa que genera un fotodiodo al ser iluminado:
R
notar que la tensión en bornes del fotodiodo es cero, o sea que
estamos en el eje de las ordenadas de su curva v-i.
iR
Vi=0
+
Vo=iR R
En esta aplicación debemos tener en cuenta que los Op-Amp no son ideales y que en realidad toman corriente
por sus terminales de entrada (para el caso del CA3140 es aproximadamente de 10pA).
Por lo tanto cuando se desea medir corrientes muy bajas, hay que tener en cuenta este dato y elegir para tal
aplicación un operacional cuya corriente de entrada sea mucho menor que la corriente a medir . Existen
operacionales denominados electrométricos con corrientes de entrada mínimas, tales como el ICH8500A de Intersil
con una Ii ≈10fA
Si tenemos en cuenta el offset de tensión veremos que este pasa a la salida directamente sin amplificar.
- Amplificador Sumador:
Veamos como al disponer esta configuración de un "cero virtual", es posible sumar las corrientes debidas a dos o
más señales distintas. En el siguiente circuito v1 y v2 crean las corrientes i1=v1/R1 y i2=v2/R2 respectivamente. Luego
la corriente que circula por el resistor R3 es el resultado de la suma de todas las corrientes i 3= i1+ i2 , ya que al
operacional no entra corriente por su terminal inversor (2)
La señal de salida será:
→ i3 R3
vO = -i3 R3 = -(i1 + i2)R3 = -(v1/R1 + v2/R2)R3
V2
vO = - (R3/R1 v1 + R3/R2 v2)
4
R2
2
3
6
Vo
Cada una de las tensiones de entrada se amplificará
por su relación de resistencias R3/Ri.
Para el caso en que R1=R2=R tendremos:
7
→i2
VCC-
+
V1
R1
-
→ i1
VCC+
vO= - (v1+v2).R3 / R
7
Ejemplo de aplicación: Medición de temperatura
Se usa el integrado AD590 que es un sensor de temperatura (-55ºC a 150ºC) que entrega una corriente IX =1µA/°K
Esta IX es aplicada a un conversor tensión-corriente, logrando de esta manera en su salida una tensión proporcional
a la misma y por lo tanto a la temperatura.
El inconveniente de este integrado es que si
Ajuste
queremos
medir en grados centígrados ya que
R
2
de Cero
VR
R3
I
el mismo nos dará una corriente de 273µA a 0°C !!.
Luego para que mida correctamente hay que
100K
res
tarle este valor.
IR=VR / R2
-12V
Esto se logra con VR y el potenciómetro R2 de tal
manera que creen una IR= VR / R2 =273µA. La
masa
I = IX - IR
corriente resultante por R3 es I = IX - IR teniendo a
virtual
4
la salida:
2 6
IX
Vout = I.R3 ( I=0 p/ 0ºC)
3
I X=1µA/ 0K
+
0
Vout =100 mV / C
7
AD 590
+12V
-12V
- Amplificador Diferencial:
Existen casos en que la señal a amplificar no es una única Vs referida a masa (single-ended), sino que hay que
amplificar la diferencia entre dos señales (v2-v1), ambas también referidas a masa. Por ej. la provenientes de
transductores en los que hay un gran nivel de contínua, como ser la salida de un puente de Wheatstone (fig.1)
Hay otros casos, en los que el nivel de ruido existente es comparable al nivel de la señal útil. En ambos casos se
debe usar un amplificador diferencial. El esquema del mismo implementado con un Op. Amp. es el siguiente:
i2
R2
Puente de
Rx
R
i1
Wheatstone :
V1
V2
Vcc
RX :variable
R
R1
V1
R
R3
V2
v-
v+
+
Vo
R4
fig.1
Calculemos la ecuación de la salida aplicando superposición :
• Considero v1 y hago v2 =0 ⇒ me queda un amplificador inversor de ganancia: - R2 / R1 ; obtengo vo´ :
R2
R1
-
v1
+
R3
•
vo´ = - v1 R2 / R1
R4
Considero v2 y hago v1 =0 ⇒ me queda un amplificador no-inversor de ganancia: 1+ R2 / R1 ; obtengo vo”:
R2
R1
+
v2
∴
vo´´ = v+ (1+ R2 / R1)
donde:
v+ = v2 R4 /(R3 + R4)
⇒
R3
vo = vo´ + vo”
R4
⇒
⇒
vo´´= v2. [R4 / (R3 + R4)] (1+ R2 / R1 )
vo = v2. [R4 / (R3 + R4)] .(1+ R2 / R1 ) - v1 R2 / R1
8
Para el caso particular en que : R1 / R2 = R3 / R4 (*) la expresión de la ganancia será:
v O ≅ ( R2 )[v 2 − v1 ]
R1
(**)
∴ La señal de salida es directamente proporcional a la diferencia entre las dos señales de entrada.
nota: Hay que ser muy cuidadoso en la selección de las resistencias para que se cumpla (*) y con ello (**).
Otro punto a tener en cuenta es que las resistencias de salida de los generadores v1 y v2 deben ser iguales ya que
estas se suman a R1 y R3 respectivamente y si no lo son ya no vale la ecuación (**) .Si esto no se cumple se puede
implementar la siguiente configuración que hace uso de dos seguidores o buffers, para adaptar impedancias.
R2
+
V1
+
R1
-
Vo=R2 / R1 (v2 -v1)
+
R1
+
R2
+
V2
Notar que si en el ejemplo del puente de Wheatstone hubiese querido medir (v2 –v1) con un amplificador inversor o
no-inversor, una de las resistencias inferiores del puente quedaría cortocircuitada.
- Amplificador Integrador:
Veamos la ecuación de la salida del siguiente circuito con realimentación negativa :
i
C
vi = iR
i
+
R
Vi
2
-
3
+
6
v o = − 1 ∫ i.dt = − 1 ∫ v dt
C
RC i
1 v .dt = K . v .dt
v = − RC
∫ i
I ∫ i
o
Vo
-
y
con
KI = − 1
RC
La salida es proporcional a la integral de la entrada, es decir que éste es un amplificador integrador. Además se
invierte la señal de entrada. Notar que si la señal de entrada tuviera un mínimo valor de contínua en poco
tiempo el operacional saturaría.
La respuesta o transferencia T, en función de la frecuencia, resulta ser:
v
T = ov
i
con
v i = iR
vo = − i jωC
y
⇒
T =−
1
1
= j
ωRC
jω RC
(*)
A diferencia de un pasa-bajos RC este integra para toda frecuencia ya que la salida estará desfasada + 90º con
respecto a la entrada. Además vemos que ITI puede ser mayor que 1.
si hacemos :
ω 1 = 1 RC
⇒
T = j.( f1 f )
⇒
T = ( f1 f )
La fig.1 muestra su comportamiento en función del tiempo y la fig.2 su respuesta en frecuencia a través del Bode.
vi
ITI [dB]
t2
t4
-20dB/década
saturación
t
log f1
vo
log f
t
fig.1
fig.2
9
Notar cómo cuando v1 vuelve a cero en t2 y en t4 la salida se mantiene en su valor negativo. Esto sucede porque el
capacitor no tiene por dónde descargarse ya que por R no circula corriente por ser cero la tensión en sus bornes y,
por el operacional tampoco ya que (idealmente) no toma corriente por sus entradas.
nota:
Es muy importante en el integrador, seleccionar un operacional de muy bajo Voff-set (así y todo muchas veces
es necesario corregirlo) ya que aunque no exista señal de entrada la tensión de off-set hará circular una corriente
constante por el capacitor de valor: VOff /R , la cual lo irá cargando lentamente, pudiendo la salida llegar a saturar.
- Comparadores:
. Comparador simple:
Debido a la muy elevada amplificación AO de los operacionales (fig.2), se los utiliza como comparadores de tensión,
(referidas a masa). Ejemplo: si A0 = 10 5 , basta (v2 – v1) = vi =100 µ V para tener a la salida una señal de 10V.
vsat+
vo [V]
Vcc+
+
v2
AO
vi
vO = AO vi = AO (v2 – v1)
-
v1
Vcc
vi [µV]
-
vsatfig.2
La señal de salida de un operacional, nunca podrá superar los valores de sus tensiones de alimentación Vcc+
y Vcc . Por ese motivo, al utilizarlo como comparador, resulta que su salida estará en el valor correspondiente a su
saturación positiva vsat+ o negativa vsat- , siempre se encontrará en alguno de esos dos estados.
VO
VO
vsat
+
Vcc
VS
vsat+
+
VS
+
Vs
Vo
-
vsat
Vcc
t
-
Vsat
-
En el esquema de la figura anterior se ha realizado una comparación con cero, pero también es posible comparar
con una tensión VR ≠ 0 .Dependiendo de que VR sea positiva ó negativa es que el diagrama anterior se corra a la
derecha ó a la izquierda del eje y respectivamente.
Si hubiésemos entrado con la señal por el terminal no-inversor los diagramas con VR=0 y VR >0 serían:
vO
Vcc+
2
VR
3
Vs
-
vO
vsat+
vsat+
6
Vo
+
Vcc-
vsat
vR
-
VR=0
vs
vR
vsat-
vs
VR>0
El inconveniente de estos comparadores es que si la señal de entrada viene acompañada de pequeñas oscilaciones
(ruido) alrededor del valor de comparación, entonces la salida cambiará continuamente de un valor de saturación al
otro. Podemos ver esto ampliado alrededor del punto de
comparación VR=0 en las figuras de la derecha:
10
. Comparador con Histéresis (Schmitt-trigger ):
Para evitar este último problema se implementa un comparador con histéresis. Este circuito hace que la tensión de
cambio para pasar de saturación positiva a negativa y viceversa no sea la misma. En todos los comparadores de
este tipo, la salida va (a través de una resistencia) a la entrada no-inversora. O sea que estamos con
realimentación “positiva” con lo cual no se cumple mas la premisa de que v+ =v .
Uno de los circuitos posibles es el siguiente:
VS
+
Ahora la salida cambiará cuando Vs sea mayor (o menor) a la
tensión en el terminal no-inversor v+.
VO
Si consideramos que el operacional no toma corriente tendremos:
R2
R1
IR2=IR1=i
VR
i
⇒
si reemplazamos (2) en (1) nos queda :
v+ = iR1 + VR
(1)
donde :
v+ = ( vO - VR)R1 / (R1+R2) + VR
⇒
i = (vO -VR) / (R1+R2)
(2)
trabajando queda:
v+ = vo R1/(R1+R2) + VR R2/(R1+R2)
Esto nos da dos valores de v+ correspondientes a los dos posibles
valores de la salida vO : Vsat+ y VsatEstos dos valores serán las tensiones de transición y valen:
vO
. v+’ = Vsat+ R1/(R1+R2) + VR R2/(R1+R2)
vsat+
v+”
. v+” = Vsat R1/(R1+R2) + VR R2/(R1+R2)
vsat-
el diagrama correspondiente es el de la derecha:
donde
v+’
vS
vR’
∆H
-
∆H
VR’=VRR2/(R1+R2)
Se define el ancho de histéresis como: ∆H = I v+’ – v+” I
En este caso será: ∆H =(Vsat+ - Vsat -) R1/(R1+R2) vemos que depende del valor de las tensiones de saturación y de
R1 y R2 elegidos.
Para el caso en que VR=0 o VR<0 los diagramas serán respectivamente:
vO
vO
vsat
vsat+
+
vR’
vS
vsat
v+’
v+”
v+’
v+”
vS
vsat
-
-
Si ahora hacemos vS senoidal y p/ VR=0 tendremos el siguiente diagrama donde se ve claramente que los valores
de cambio difieren, con lo que si existiera ruido alrededor de dichos valores no afectaría a la salida. A no ser que la
perturbación fuera muy grande, en ese caso deberíamos ampliar el ancho de histéresis ∆H.
vO
vsat+
vS
v+’
v+”
t
vsat11
Si la señal hubiera entrado por el terminal no-inversor el diagrama de histéresis para VR >0 sería:
vO
VR
+
vsat+
Vo
v+”
v+’
vR’
Vs
R1
vsat
R2
vS
-
∆H
notas:
• El comportamiento de los comparadores con histéresis tiene su explicación en que en estos circuitos la
realimentación es positiva, o sea que parte de la salida vuelve al terminal no-inversor contrariamente a lo que
vimos en los circuitos anteriores. Siempre que haya realimentación positiva la salida valdrá Vsat+ ó Vsat- .
•
En principio debido a la gran ganancia que poseen los operacionales, cualquiera podría trabajar como
comparador sin embargo existen operacionales especiales para esta función que tienen mayor ganancia y son
más veloces. Además de soportan mayores tensiones a su entrada como por ejemplo el LM311.
- Conversor Tensión - Corriente:
El siguiente es un caso particular de los conversores tensión-corriente vistos hasta ahora (podemos pensar a los
amplificadores inversor y no-inversores como de este tipo).
En este caso adaptamos un no-inversor conjuntamente con un transistor para construir una fuente de corriente
donde RL está conectada a masa. [Un no-inversor también es una fuente de corriente con IL = Vs/R1 y donde la carga
es RL≡R2 pero en este caso no está conectada a masa].
La realimentación negativa sigue existiendo ahora a través del transistor. Esta hace que la tensión en los terminales
inversor v- (2) y no-inversor v+ (3) sean prácticamente iguales.
Luego tendremos que :
v+ = v - = vi
12V
Además : v -≡ ve
Con lo que podemos calcular la corriente i a través
de R :
RL
vi
i = (VCC - ve) / R = (VCC – vi) / R
3
+
Ic ≡ i
6
2
2A257
Con lo cual para una dada tensión de entrada vi y, para
una dada Vcc podemos fijar el valor de i variando R.
Ya que la corriente de emisor Ie ≡ i es prácticamente igual
a la corriente de colector Ic , será esta la que circule por la
carga RL independientemente de su valor, dentro de ciertos límites (*)
O sea que el circuito se comporta como una fuente de corriente i.
-12V
ve
R
i
VCC
(*) nota:
Como en todas las fuentes de corriente existe un valor máximo de tensión VLmáx a su salida, en este caso no podrá
superar a ≈ ve . Este valor máximo a su vez me fija un máximo valor de carga RL tal que RLmáx = VLmáx / i
12
Apéndice - CMRR
Tensiones a modo común en las configuraciones no-inversora e inversora:
Habíamos visto que en un Amplificador operacional real, la salida respondía tanto al valor de tensión
diferencial de las entradas: vd = v2 –v1, como al valor de tensión en modo común vc= (v2 +v1)/2 . La ecuación
que refleja esto es la siguiente:
vo = Ad vd + Ac vc
(1)
Donde Ad es la ganancia en modo diferencial y Ac es la ganancia en modo común. Siendo la relación entre
ellas: CMRR = Ad / Ac el cual es un dato provistp por el fabricante.
Si en (1) reemplazamos Ac por Ad /CMRR, la ecuación anterior la podemos escribir de la siguiente forma:
vo = Ad.vd + Ad.vc /CMRR (2)
v1
con lo cual podemos tener el siguiente modelo circuital
ya que: vd = v2 – v1
vc/CMRR
+
+
v2
Ad
vo
CMRR en el Amplificador no-inversor:
Hasta acá vimos cual es la influencia de la tensión a modo común en un Amplificador Operacional trabajando
sin ningún tipo de realimentación. Veamos ahora el caso de su influencia en un amplificador no-inversor.
El circuito teniendo en cuenta vc será:
En este caso se cumple que la tensión a modo común es: vc= vs
R2
-
R1
+
La ganancia de tensión es Av= vo/vs (*)
vC/CMR
+
vS+
-
vs= vi - vc/CMRR + vR1
- +vi + Ad
Vo
vR1 = vo R1/ (R2 +R1)
dónde:
∴
con
vo = vi ..Ad
vi Ad
A =
v
[ v i − CMRRc + v i A d R 1 ]
v
( R1 + R 2 )
si pasamos vi . Ad al denominador y reemplazamos vc por vs nos queda:
A =
v
[ 1
A
d
1
−
+
vs
v i ⋅ A d ⋅CMRR
R1
]
( R1 + R 2 )
A =
;
[ 1
A
d
v
1
−
vs
v o ⋅CMRR
+
R1
]
( R1 + R 2 )
como : Av= vo/vs la ecuación anterior será :
A =
v
A
v
=
[ 1
Ad
−
1
1
A v ⋅CMRR
+
R1
]
( R1 + R 2 )
si despejamos Av tendremos que :
1+
[
1
CMRR
R1
1 +
]
Ad
( R1 + R 2 )
cómo Ad >>1
⇒
A = (1 +
v
1
CMRR
).( 1 +
R
R
2 )
1
Resultado al que podemos llegar si consideramos vi=0 y aplicamos superposición.
CMRR en el Amplificador inversor:
- En la configuración “inversora” el generador de tensión a modo común (vc /CMRR) no afecta, ya que
vc=0.
13
Ejemplo de aplicación: Punta Fría
Veamos cómo podemos compensar electrónicamente una termocupla. Supongamos que tenemos que medir
temperaturas Tc alrededor de los 300 °C con una termocupla tipo T (40 µV/°C) y que deseamos una salida de
10 mV/°C. Podríamos implementar un amplificador no-inversor de ganancia:
AV = (1+ R4/ R1) = 10mV /40µV = 250
Supongamos que elegimos entonces:
El circuito sería el siguiente:
R4
;
El problema de este circuito es que la salida
vo será cero cuando Tc sea igual a Tamb ya
que Vtc=0V .
Tendríamos una curva como la (a):
+Vcc
7
2
1k
-
6
OP07
3
+
VO [mV]
(b)
VO = Vtc (1+R4/R1)
4
(a)
K
+
-Vcc
Vtc
TC
VO= Tc .10mV/°C
R4 ≈ 250k y R1=1k
250k
R1
tal que :
0
-
Tamb
Tamb
T [°C]
De la gráfica vemos que para pasar de la curva (a) a la (b) tenemos que sumar un valor constante
K =Tamb x40µV/ºC. Para conseguir esto podemos hacer lo siguiente:
donde Vamb producirá una salida:
R4
250k
R2
Vamb
VO’ = -Vamb R4 / R2 = K
+Vcc
55k
R1
que se sumará a la salida provocada por la
termocupla .
7
2
1k
3
OP07
+
6
VO = Vtc (1+R4/R1) - Vamb R4/R2
4
VO = Vtc (1+R4/R1) - Vamb R4/R2
Vamb debe ser negativa para que
efectivamente halla una suma
+
Vtc
TC
-Vcc
-
Tamb
De esta manera pasaríamos a la curva (b) referída a 0 °C. Esta solución es precaria porque sirve
como compensación para una única temperatura ambiente . Vemos que si por ej. aumenta la
temperatura ambiente la curva (a) se correrá a la derecha con lo cual cambiará el valor de K a sumar.
La solución es que la tensión Vamb sea proporcional a la temperatura ambiente, esto se puede
implementar con la propiedad de los diodos cuya tensión directa varía apróximadamente: -2,2mV/°C.
Por ser más lineal, se usa un transistor como diodo (cortocircuitando la juntura colector –base).
Existen transistores especiales como los npn MTS102 /103/105 de Motorola .
Los -2,2mV/°C del transistor deben ser amplificados tal que:
-2,2mV /°C (- R4 / R2) =10mV/°C
⇒ R2 =(2,2mV/°C / 10mV/°C).R4
14
cómo R4 ya está fijada por la ganancia que le dimos a la termocupla, obtenemos R2.
si
R4 ≈ 250k
⇒
R2 ≈ 55k
Vcc+
R6
R4
250k
R2
Vamb
+Vcc
55k
R1
7
2
1k
3
OP07
+
4
6
VO = Vtc (1+R4/R1) - Vamb R4/R2
+
-Vcc
Vtc
TC
-
Tamb
El problema estaría solucionado sino fuera porque el transistor me da una tensión Vγ de apróx. 0.6V @ 0 °C.
∴ La tensión que me da el mismo será:
Vamb = Vγ -2,2mV/°C .Tamb
O sea que debemos restar Vγ. Para eso agregamos otra rama al sumador alimentada por VR tal que:
VR
Vcc+
VR . R4 / R3 ≈ - Vγ . R4 / R2
R3
VR ≈ - Vγ . R3 / R2
R4
R6
(negativa)
250k
R2
Vamb
+Vcc
55k
R1
7
2
1k
3
OP07
+
4
6
VO = Vtc (1+R4/R1) - Vamb R4/R2 - VR R4/R3
+
Vtc
TC
-Vcc
-
Tamb
Los pasos a seguir para calibrar este circuito son:
1) Fijar la ganancia de la termocupla para lograr la salida deseada (10mV/°C). Para eso se puede aplicar una
pequeña tensión conocida en lugar de la termocupla (poniendo Vamb y VR a cero) y ajustar R4 para lograr la
ganancia AV tc = 1+ R4/R1 =10mV/40µV . Hecho esto R4 queda fijada y no se vuelve a ajustar!!.
2) Fijar la ganancia de Vamb (poniendo Vtc y VR a cero) tal que AV Vamb=1+ R4/R2 =10mV / 2,2mV
Cada transistor tiene su propio coeficiente de variación con la temperatura ese es valor que hay que colocar en
lugar de 2,2mV para setear la ganancia AV Vamb . Igual que en el paso 1) coloco una tensión conocida en lugar
de Vamb y variando R2 busco que la salida cumpla con el valor que le corresponde a AV Vamb.
3) Por último debo hacer el ajuste de cero, que anula la tensión que da el transistor a 0 °C. Lo hacemos variando
R3 de tal manera que la salida cumpla con el valor que le corresponda para una determinada temperatura de
medición Tc ; si Tc=0 °C ⇒ VO= 0V
15
Nota: Para este circuito usamos un operacional de bajo off-set de tensión como ser el OP07 (≈30µV).
16