Cuestiones
Anuncio
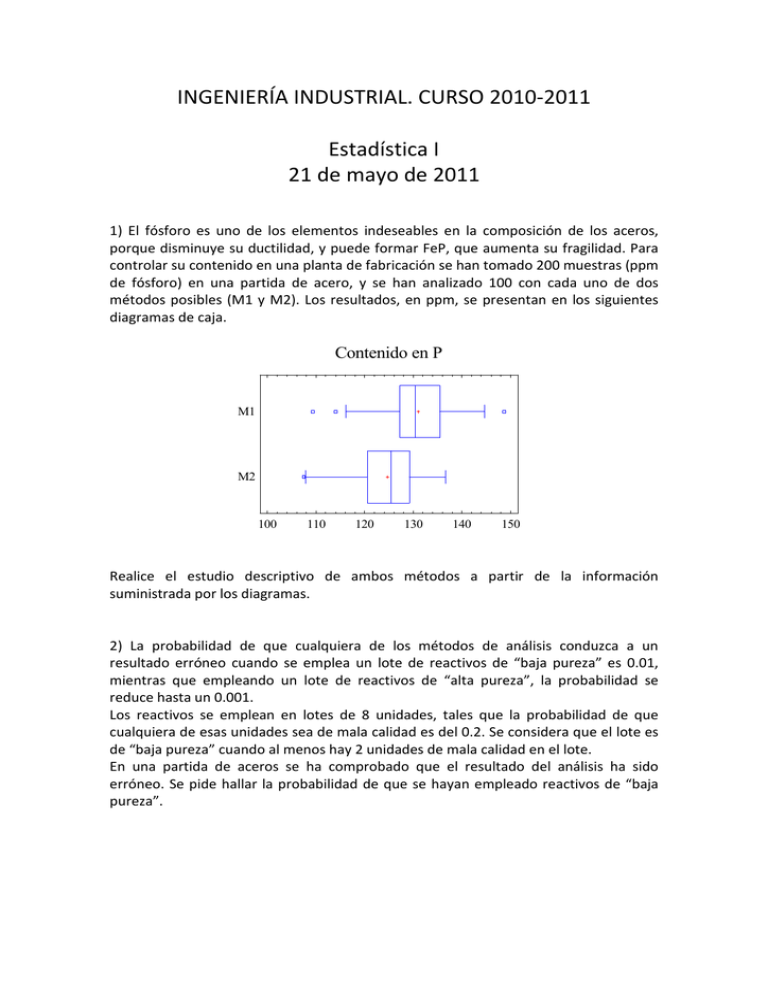
INGENIERÍA INDUSTRIAL. CURSO 2010-2011 Estadística I 21 de mayo de 2011 1) El fósforo es uno de los elementos indeseables en la composición de los aceros, porque disminuye su ductilidad, y puede formar FeP, que aumenta su fragilidad. Para controlar su contenido en una planta de fabricación se han tomado 200 muestras (ppm de fósforo) en una partida de acero, y se han analizado 100 con cada uno de dos métodos posibles (M1 y M2). Los resultados, en ppm, se presentan en los siguientes diagramas de caja. Contenido en P M1 M2 100 110 120 130 140 150 Realice el estudio descriptivo de ambos métodos a partir de la información suministrada por los diagramas. 2) La probabilidad de que cualquiera de los métodos de análisis conduzca a un resultado erróneo cuando se emplea un lote de reactivos de “baja pureza” es 0.01, mientras que empleando un lote de reactivos de “alta pureza”, la probabilidad se reduce hasta un 0.001. Los reactivos se emplean en lotes de 8 unidades, tales que la probabilidad de que cualquiera de esas unidades sea de mala calidad es del 0.2. Se considera que el lote es de “baja pureza” cuando al menos hay 2 unidades de mala calidad en el lote. En una partida de aceros se ha comprobado que el resultado del análisis ha sido erróneo. Se pide hallar la probabilidad de que se hayan empleado reactivos de “baja pureza”. 3) Tras varios ensayos, el ingeniero de calidad de la planta anterior decide emplear M1 para el control de la cantidad de de fósforo. Para ello, se toman 14 medidas al día y se calcula su media. Se sabe que, para el sistema de producción empleado, la variable aleatoria X: “contenido de fósforo del material (ppm)” sigue una distribución: N(131, 13.0962). a) Calcule la probabilidad de que la cantidad media de impurezas determinada en 2 días distintos difiera entre sí más de 2.5 ppm. b) ¿Cuántas medidas habría que tomar para que con probabilidad mayor de 0.99, la cantidad media de impurezas difiera de 131.5 ppm en menos de 0.5 ppm? 4) Aunque el ingeniero de calidad había decidido usar M1, la verdad es que M2 resultaba mucho más cómodo de realizar en el laboratorio. Sería interesante comprobar si las menores cantidades de impurezas detectadas por M2 son reales o fruto del azar, para lo cual se plantea un contraste de hipótesis. Determinar si efectivamente la cantidad media de fósforo detectada con M1 es mayor que con M2, utilizando los datos muestrales (en ppm) de la tabla adjunta, al nivel de significación del 0.01, y considerando normalidad y varianzas poblacionales iguales. Media M1 M2 131 125 Cuasidesviación n tipica 6 20 7 25 5) Finalmente se decide controlar la calidad mediante gráficos de medias y rangos para la variable resiliencia (cantidad de energía que un material puede absorber al romperse por efecto de un impacto, por unidad de superficie de rotura). Con el proceso en estado de control, 50 / . Si la capacidad estimada del proceso es 18 y el tamaño de cada muestra es 5, se pide: a) Calcule los límites de control para el gráfico de medias. b) Por causas desconocidas, la media del proceso desciende hasta un valor de 47.5 ¿Cuál es la probabilidad de detectar este desajuste? c) Calcule la probabilidad de que las tres muestras siguientes al desajuste del apartado b) estén dentro de los límites de control. d) Calcule la probabilidad de que, de las tres muestras siguientes al desajuste del apartado b, una o más se salga fuera de los límites de control. Algunas probabilidades , 3.01327 0.995 2.41625 0.99 2.41414 0.99 2.69511 0.995








