AHP Datei - Campus Virtual

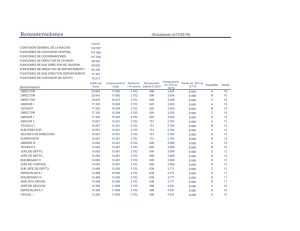
FACULTAD DE INGENIERÍA
ESCUELA DE INGENIERÍA INDUSTRIAL
AHP - Analytic Hierarchy Process
Análisis Multicriterio en la Toma de
Decisiones
Usando la PL se ha abordado el soporte cuantitativo a decisiones que
representan un único objetivo: maximizar ganancias, minimizar costos,
minimizar desperdicios, etc.
Muchas situaciones del mundo real necesitan que el decisor considere
múltiples objetivos relacionados con una única situación.
Considérese el proceso de decisión al respecto de la mejor
localización de una nueva sucursal de una empresa. Dado que el costo
del terreno y la construcción de la nueva instalación puede variar de un
sitio a otro, ese objetivo puede convertirse en un criterio de decisión
al respecto de la mejor localización, esto es, costo más bajo. Sin
embargo, otros aspectos como: disponibilidad de infraestructura para
transporte y servicios básicos, facilidad para contratación de
personal, tasas impositivas, entre otros, podrían quedarse por fuera
de un modelo cuyo objetivo es únicamente la reducción de costos.
Análisis Multicriterio en la Toma de
Decisiones
Modelo de Decisión Simple con Atributos Múltiples /
Scoring
Pretende la clasificación de las alternativas indicando la preferencia
general asociada a cada una de ellas, de modo que pueda identificarse
“la mejor”.
El decisor debe establecer la importancia relativa de cada uno de los
objetivos (ponderaciones) para luego proceder a la definición de una
estructura de preferencias entre las alternativas identificadas.
Usando una escala de medición común, como 1 – 10 (1, lo peor, 10, lo
mejor), se establece un orden jerárquico entre las alternativas, al
respecto de cada objetivo que se desee evaluar.
La importancia relativa de cada objetivo en conjunto con la posición
de cada alternativa según la escala común que se usa para ordenarlas,
entrega un índice agregado que permite decidir cual es la mejor de las
alternativas, “promediando” la importancia de todos los objetivos
tenidos en cuenta.
Modelo Simple con Atributos Múltiples /
Scoring
Etapas del Modelo
1.
2.
3.
4.
5.
6.
7.
Identificar la meta general del problema.
Identificar las alternativas.
Listar los criterios a emplear en la toma de la decisión.
Asignar una ponderación para cada criterio de decisión.
Establecer en cuanto satisface cada alternativa el nivel de cada
uno de los criterios.
Calcular el puntaje total de cada alternativa.
Ordenar las alternativas en consideración de acuerdo al puntaje
obtenido en el paso anterior. La alternativa con el puntaje más
alto representará la mejor del conjunto inicial de alternativas.
Esquema del Modelo
S j   wi rij
i
• Sj, es el puntaje total de cada alternativa.
• wi, es la ponderación de cada criterio.
• r ij, Valoración de la alternativa j al respecto del
criterio i.
Modelo Simple con Atributos Múltiples /
Scoring
Ejemplo
Un recién graduado de la Escuela de Negocios, con especialización en
finanzas y contabilidad, ha recibido las siguientes ofertas de empleo:
a) Analista financiero para un estudio de mercado en Medellín
b) Contador para una empresa industrial en Bucaramanga
c) Auditor de una firma de consultores en Bogotá.
El recién graduado maneja múltiples criterios para tomar su decisión,
y así, por ejemplo, cree que el puesto de analista financiero es la
mejor oportunidad para mejorar su posición a largo plazo, prefiere, sin
embargo, vivir en Bucaramanga,
y considera que la firma de
consultores bogotanos tiene la mejor filosofía laboral, y por tanto el
mejor ambiente de trabajo.
Modelo Simple con Atributos Múltiples /
Scoring
… Ejemplo
Objetivo: Seleccionar la mejor oferta de empleo.
Alternativas:
1 =Analista Financiero en Medellín
2 = Contador en Bucaramanga
3 = Auditor en Bogotá.
Criterios:
1 = Avance de la carrera
2 = Localización
3 = Estilo administrativo
4 = Remuneración
5 = Prestigio
6 = Seguridad en el empleo
7 = Calidad en el trabajo
Criterios
1
2
3
4
5
6
7
Asignación de ponderaciones a cada criterio
1 = Muy poco importante
2 = Poco importante
3 = Importancia media
4 = Algo importante
5 = Muy importante
Avance de la carrera
Localización
Estilo administrativo
Remuneración
Prestigio
Seguridad en el empleo
Calidad en el trabajo
Ponderación
5
3
4
3
2
4
5
Modelo Simple con Atributos Múltiples / Scoring
… Ejemplo (Pasos)
Asignación de ponderaciones a cada alternativa en cada criterio
1 = extra bajo
Medellín
Bucaramanga
2 = muy bajo
Criterios
Analista Fin.
Contador
3 = bajo
1 Avance de la carrera
8
6
4 = poco bajo
2
Localización
3
8
5 = medio
3 Estilo administrativo
5
6
6 = poco alto
4 Remuneración
6
7
7 = alto
5 Prestigio
7
5
8 = muy alto
6 Seguridad en el empleo
4
7
9 = extra alto
7 Calidad en el trabajo
8
6
Criterios
1
2
3
4
5
6
7
Ponderación
Avance de la carrera
Localización
Estilo administrativo
Remuneración
Prestigio
Seguridad en el empleo
Calidad en el trabajo
PUNTAJE TOTAL
5
3
4
3
2
4
5
Medellín
Bucaramanga
Analista Fin.
Contador
8
3
5
6
7
4
8
157
6
8
6
7
5
7
6
167
Bogotá
Auditor
4
7
9
5
4
6
5
Bogotá
Auditor
4
7
9
5
4
6
5
149
Modelo Simple con Atributos Múltiples /
Scoring
Ejemplo II
Usted debe decidir al respecto del proceso de compra de un nuevo
computador para su oficina. Debe elegir entre tres posibles
computadoras, que ya han sido referidas por sus proveedores: (1) el
modelo A que funciona a base de un procesador XEON a 1.6 GHz, (2)
el modelo B que funciona con un procesador Pentium IV a 1.33 GHz y
(3) el modelo C cuyo procesador es un PowerPC a 2.0 GHz.
Los criterios relevantes para el caso son: el precio, la velocidad del
reloj del procesador, la capacidad del disco duro y la garantía o
soporte técnico ofrecido por el proveedor de la máquina. Después de
una reunión con la gerencia se ha decidido que el precio tendrá el 50%
de la ponderación total al tomar la decisión, la velocidad tendrá una
importancia relativa del 15%, la capacidad del disco duro 20% y el
restante 15% se asignará a la garantía y soporte técnico ofrecido.
Modelo Simple con Atributos Múltiples /
Scoring
… Ejemplo II
Usando una escala 1-10 para valorar las diferentes alternativas, se ha
llegado a la siguiente tabla de ponderaciones:
1
2
3
4
Criterios
Ponderación
Modelo A
Modelo B
Modelo C
Precio
Velocidad procesador
Capacidad Disco duro
Garantía
50%
15%
20%
15%
5
7
9
7
8
5
4
10
3
9
10
7
Total
100%
6,4
7,1
5,9
Puede observarse que el modelo B ofrece el mayor puntaje total, y por
tanto, será el equipo elegido usando esta metodología.
Análisis Multicriterio / AHP (Analytic
Hierarchy Process)
¿Qué es AHP
Analítica)?
(PJA
–
Proceso
de
Jerarquía
Es un método cuantitativo desarrollado por Thomas L. Saaty en 1970
que busca ordenar alternativas en un proceso de decisión, de modo que
se pueda seleccionar una en particular bajo un panorama de múltiples
criterios. AHP es un proceso que obtiene un índice numérico que
permite ordenar las alternativas de acuerdo al nivel de satisfacción
que cada una de ellas muestra al respecto de los criterios exigidos por
el decisor.
El índice final que se obtiene para cada alternativa es similar al
obtenido con la técnica Scoring, pero las ponderaciones de criterios y
las calificaciones de las alternativas se obtienen por comparaciones
sucesivas.
Proceso de Jerarquía Analítica (AHP)
¿Jerarquía Analítica…. ?
Las decisiones que consideran múltiples criterios admiten una
representación jerárquica, similar en principio a un organigrama, que
denota la manera en que se estructura el proceso de decisión.
Proceso de Jerarquía Analítica (AHP)
¿Tabla estandarizada de preferencias?
Juicio verbal de preferencia
Preferencia
Preferencia
Preferencia
Preferencia
Preferencia
Preferencia
Preferencia
Preferencia
Preferencia
igual
igual a moderada
moderada
moderada a fuerte
fuerte
fuerte a muy fuerte
muy fuerte
muy fuerte a extrema
extrema
Valor numérico
1
2
3
4
5
6
7
8
9
Se recomienda trabajar siempre con esta tabla, que ha sido probada
muchas veces por personas expertas en el uso de la herramienta,
quienes han podido constatar que se adecua muy bien a los propósitos
de clasificación del nivel de preferencia.
Proceso de Jerarquía Analítica (AHP)
Etapas del Modelo AHP
1.
Descomponer el problema de decisión en una jerarquía de
elementos relacionados, identificando:
a) La meta general
b) los criterios (i =1, 2, .., m) y
c) Las alternativas posibles (j = 1, 2, .., n)
Para cada uno de los m criterios repetir las etapas 2 a 5:
2.
3.
4.
Desarrollar la Matriz de Comparación por Pares de Alternativas
(MCP) para cada criterio en consideración, usando para ello la
escala de valoración estándar.
Desarrollar la Matriz Normalizada (MCN), dividiendo cada
elemento de una columna entre la suma de todos los elementos en
ella.
Desarrollar el Vector de Prioridad para el criterio calculando el
promedio de cada fila de la matriz normalizada. Dicho vector
califica cada alternativa al respecto del criterio con que se esté
trabajando.
Proceso de Jerarquía Analítica (AHP)
… Etapas del Modelo AHP
5.
La consistencia de las opiniones utilizadas en la matriz de
comparación por pares puede ser determinada a través del
indicador Cociente de Consistencia (CR). Un CR inferior a 0.10 es
considerado aceptable, o lo que es lo mismo, indica consistencia en
la calificación por pares de alternativas al respecto del criterio.
Si el CR resulta ser mayor que 0.10, entonces han de revisarse las
opiniones y/o juicios que han sido usados para completar la matriz.
6.
Después de culminar la secuencia 2 - 3 - 4 – 5 para todos los
criterios usados, los resultados se resumen en la llamada Matriz
de Prioridades (MP), listando las alternativas por cada fila, y los
criterios por columna.
7.
Desarrollar la Matriz de Comparación de Criterios, por parejas de
ellos, usando la misma metodología que se siguió para la
construcción de la Matriz de Prioridades.
Proceso de Jerarquía Analítica (AHP)
… Etapas del Modelo AHP
8.
Desarrollar el Vector de Prioridad Global multiplicando el vector
de prioridad de los criterios (Paso 7) por la Matriz de Prioridad
de las Alternativas (Paso 6).
Cálculo del Coeficiente de Consistencia (CR)
1.
2.
3.
4.
Para cada línea de la Matriz de Comparación por Pares,
determinar la suma ponderada, en base a la suma de los productos
del valor de cada celda por la respectiva prioridad de cada
alternativa.
Para cada línea del vector resultante, dividir el valor ponderado
que representa entre la prioridad de su alternativa
correspondiente.
Determinar la media del resultado del paso anterior ( máx)
Calcular el Índice de Consistencia para cada criterio/alternativa
como:
máx

n
CI 
n 1
Proceso de Jerarquía Analítica (AHP)
… Cálculo del Coeficiente de Consistencia (CR)
5.
Determinar el índice RI (Random Index) según la tabla siguiente:
Total de
Índice
Alternativas
Aleatorio (RI)
3
4
5
6
7
8
9
10
6.
Calcular CR como:
0,58
0,90
1,12
1,24
1,32
1,41
1,45
1,49
Los valores de RI se han
obtenido
a
partir
de
simulación, calculando el valor
CI para muchas matrices de
cada tamaño n, con valores
aleatorios.
CI
CR 
RI
Proceso de Jerarquía Analítica (AHP)
Ejemplo
Chucho está buscando un nuevo servidor para su naciente empresa de
alojamiento de páginas Web. Él ha determinado que, en general, son
tres los factores preponderantes en su decisión al respecto del nuevo
servidor: características de los elementos hardware, software de
soporte a las tareas administrativas propias del servidor y el soporte
técnico del vendedor de la máquina.
Chucho sabe que el esquema de su modelo de decisión puede ser visto
como una jerarquía, representada por el siguiente diagrama:
S e le c c io n a r e l m e jo r se r v id o r
H ardw are
S ist. A
S ist. B
S oftw are
S ist. C
S ist. A
S ist. B
Vendedor
S ist. C
S ist. A
S ist. B
S ist. C
Proceso de Jerarquía Analítica (AHP)
… Ejemplo
Chucho ha decidido usar la técnica AHP para orientar su decisión
respecto a la compra del nuevo servidor. Iniciando con el factor
“hardware” y usando la escala estandar de preferencia, ha
determinado que el hardware del Sistema A es moderadamente
preferido al del Sistema B, en tanto el nivel de preferencia respecto
al hardware del Sistema A sobre el Sistema C es de preferencia
extrema. La preferencia según el hardware entre los sistemas B y C,
en ese orden, es entre fuerte y muy fuerte.
Según lo anterior, la Matriz de Comparación por Pares (MCP) para el
criterio Hardware sería:
HARDWARE
SIST. A
SIST. B
SIST. C
SIST. A
1
3
9
SIST. B
1/3
1
6
SIST. C
1/9
1/6
1
Proceso de Jerarquía Analítica (AHP)
… Ejemplo
Ahora han de realizarse los cálculos para hallar la Matriz Normalizada
(MCN):
Totales por columna.
HARDWARE
SIST. A
SIST. B
SIST. C
SIST. A
1
3
9
SIST. B
1/3
1
6
SIST. C
1/9
1/6
1
1.444
4.1667
16
TOTALES
Matriz Normalizada
HARDWARE
SIST. A
SIST. B
SIST. C
SIST. A
0.6923
0.72
0.5625
SIST. B
0.2308
0.24
0.375
SIST. C
0.0769
0.04
0.0625
Proceso de Jerarquía Analítica (AHP)
… Ejemplo:
Hardware:
Luego se calcula el Vector de Prioridades para el criterio
HARDWARE
Vector de Prioridades - Hardware
SIST. A
SIST. B
SIST. C
SIST. A
0.6923
0.72
0.5625
0.6583
SIST. B
0.2309
0.24
0.375
0.2819
SIST. C
0.0769
0.04
0.0625
0.0598
1.0
1.0
1.0
1.0
TOTALES
Se chequea la coherencia en el uso de la
escala al construir la Matriz de
Comparaciones, calculando el CR:
Suma
Ponderada
2.0423
0.8602
0.1799
Vector
Ponderado
Proceso de Jerarquía Analítica (AHP)
… Ejemplo
Se calcula el Vector de Consistencia, lambda, el Índice de Consistencia
(CI) y el Coeficiente de Consistencia (CR):
Suma Ponderada/ Vector prioridad|
Vector de
Consistencia
2.0423/0.685
3.1025
0.8602/0.2819
3.0512
0.1799/0.0598
3.0086

CI
3.1025  3.0512  3.0086
 3.0541
3
máx  n
n 1

3.0541  3
 0.0270
31
CI 0.0270
CR 

 0.0466
RI
.58
Al ser menor
que 0.1 avala
los cálculos!
Proceso de Jerarquía Analítica (AHP)
… Ejemplo
Las Matrices de Comparación por Pares para Software y Vendedor
son, respectivamente:
SOFTWARE
Sist. A
Sist. B
Sist. C
Sist. A
1
2
8
Sist. B
VENDEDOR
Sist. A
Sist. B
Sist. C
Sist. A
1
Sist. B
1
1
1
5
Sist. C
1
Sist. C
6
3
1
Proceso de Jerarquía Analítica (AHP)
… Ejemplo
Ahora hay que determinar el peso que tendrá cada factor en la
decisión final, es decir, la ponderación de cada factor.
Se ha determinado que el software es el factor más importante. La
preferencia del factor software sobre hardware oscila entre muy
fuerte a extremadamente fuerte (8); el software se prefiere
moderadamente en comparación al soporte del vendedor (3) y, por
último, se prefiere moderadamente el soporte del vendedor en
comparación al hardware (3). La MCP sería entonces:
C RITERIO
Software
Hardware
Vendedor
Software
1
1/8
1/3
Hardware
8
1
3
Vendedor
3
1/3
1
Proceso de Jerarquía Analítica (AHP)
La matriz Normalizada el anáalisis de consistencia
son como siguen
Matriz de Normalizada para el criterio valor
SOFTWARE HARDWARE VENDEDOR
SOFTWARE
24/35
2/3
9/13
HARDWARE
3/35
1/12
1/13
VENDEDOR
8/35
1/4
3/13
Vector Prioridad
Análisis de sensibilidad
Luego la decisión debería ser adquirir el Sistema C.
Suma
Sum. Pond.
Índice de
Índice
 máxima
Ponderada Vect. Prior.
Consistenci Aleatorio
2.0571
3.0183
3.0198 0.00988188
0.58
0.2476
3.0201
0.7143
3.0209
0.68
0.08
0.24
Razon de
Consistencia
0.017
Proceso de Jerarquía Analítica (AHP)
… Ejemplo
La tabla final es:
FAC TOR
Software
Hardware
Vendedor
P untaje Total
Evaluación del Factor
Sist. A
Sist. B
Sist. C
0 ,0 874
0 ,16 22
0 ,750 4
0 ,6 853
0 ,2819
0 ,0 59 8
0 ,49 6 7
0 ,39 6 7
0 ,10 6 6
0 ,2332
0 ,2275
0 ,5416
Luego la decisión debería ser adquirir el Sistema C.
P onderación
0 ,6 816
0 ,0 820
0 ,236 4
Proceso de Jerarquía Analítica (AHP)
Matrices de comparación por pares por criterios
Matrices
Matriz de
deComparación
comparaciónpor
porPares
paresde
porsubcriterios
criterios y subcriterios para todas las alternativas
Precio
Contr. 1
Fallas
Precio
Contr. 1
Fallas
Precio
11
Contr. 2
SobreCos
Cap.Finan
21/2
Contr.
3
Demoras
Desem. Pas
1/3
1/2
Calidad
Experiencia
1/5
1/5
Matriz
normalizada
Recursos
1/6
Contr. 2
Contr. 3 PasCalidad
SobreCos
Cap.Finan
Demoras
Desem.
Experiencia Recursos
Juicio verbal de preferencia
Valor numérico
1
1/2
2 1/7
32 1/5
55
6
1
7
1
3
11
53
35
7Preferencia igual
Preferencia
igual
a
moderada
2
5
1/3
1
1/5
1/3
11
12
6
Lam bda
4,13
3
Lam bda
5,18
1/3
1/5
11/2
11
2Preferencia moderada
CI
0,04
Preferencia
moderada
a
fuerte
4
CI
0,05
1/7
1/6
1/2
1
¿Qué sucede cuando no se llega
Contr. 1
Contr. 2
Contr. 3
Prioridad
Matriz
normalizada
a
un
Contr.
1 consenso?
0,08
0,10
0,05
0,07
Matriz normalizada
Preferencia
Preferencia
Desempeño
pasado
Contr. 2
0,54 Fallas 0,68 SobreCos
0,71 Demoras 0,64Calidad Preferencia
Criterios
Precio
Cap.Finan
Desem.
Pas
Experiencia
Recursos
Fallas
0,280,23
0,250,24
0,30
0,50 Preferencia
Contr. 3
0,38
0,23
Precio
0,42
0,54
0,30
0,37
0,27
SobreCos
0,57
0,49
0,50
0,30
Preferencia
Precio
Cap.Finan
Dem
oras
Lam bda
Desem. Pas
Calidad
CI
Experiencia
CR
Recursos
0,21
3,07
0,21
0,03
0,08
0,06
0,07
0,27
0,09
0,09
0,06
0,45
0,10
0,15
0,16
0,37
0,10
0,15
0,10
0,32
0,10
0,27
0,10
0,05
0,08
0,07
0,09
0,04
0,03
0,04
0,05
CR
0,05
fuerte
CR
0,04
fuerte a muy fuerte
muy
fuerte
Prioridad
Prioridad
muy0,33
fuerte a extrema
0,38
extrema
4.24
0,46
0,10
0,11
0,32
0,17
0,08
0,04
5
6
7
8
9
Proceso de Jerarquía Analítica (AHP)
Ponderaciones
Ponderaciones
parciales
Precio
38%
Capacidad Financiera
32%
Estados Financieros
Referencias Financieras
Criterios y Subcriterios
Desempeño Pasado
Contratista
Contratista
Contratista
totales
Uno
Dos
Tres
38%
7%
64%
28%
86%
28%
77%
11%
12%
14%
5%
79%
13%
8%
17%
Fallas en culminación
33%
6%
76%
7%
17%
Sobrecostos
46%
8%
40%
20%
40%
Demoras
10%
2%
72%
17%
11%
Nivel de calidad actual
11%
2%
71%
20%
9%
Experiencia
8%
Magnitud de proyectos
64%
5%
77%
16%
7%
Tipo de proyectos
9%
1%
65%
25%
10%
Experiencia Local
27%
2%
15%
67%
18%
Recursos
4%
Recursos físicos
83%
4%
14%
33%
52%
Recursos humanos
17%
1%
67%
23%
10%
43,65%
34,55%
21,80%
Calificación Total