modelo didáctico para el análisis experimental de las propiedades
Anuncio

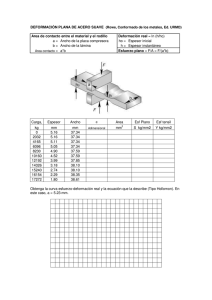
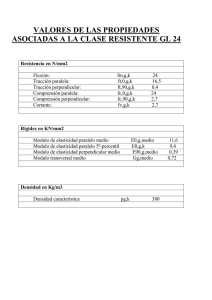
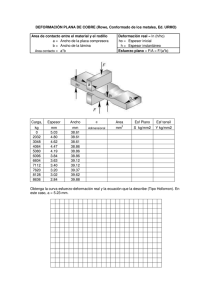
REVISTA COLOMBIANA DE FISICA, VOL. 33, No. 2. 2001 MODELO DIDÁCTICO PARA EL ANÁLISIS EXPERIMENTAL DE LAS PROPIEDADES ELÁSTICAS DE LOS MATERIALES Francisco Ernesto Cortés Sánchez Fundación Interamericana Técnica F.I.T. Santafé de Bogotá, Colombia RESUMEN Una opción para optimizar el proceso de aprendizaje de la física, es la experimentación con equipos diseñados y fabricados por el mismo estudiante. Y aunque su eficiencia no sea la de un equipo de alta tecnología, ni esto se pueda llevar a cabo en cada práctica, la construcción del equipo de laboratorio permite, además de la experimentación, el estudio del funcionamiento y de la interconexión de sus componentes. Por otro lado, esto representaría una ventaja para las instituciones, principalmente las de recursos limitados, ya que sus laboratorios adquieren equipos a muy bajo costo, con implementos "sencillos", y con tecnología propia. Teniendo en cuenta estos aspectos, la F.I.T. ha dotado sus laboratorios con equipos de vacío, trasferencia de calor, fluidos y electromagnetismo entre otros, diseñando en cada caso experimentos tanto cualitativos como cuantitativos. En este caso, se diseñaron y construyeron dos máquinas mecánicas para el estudio de la elasticidad. Una de tracción y la otra de corte, con las que se determinaron los módulos de Young y de corte respectivamente para diversos materiales. Con la primera se tensionaron de forma gradual, alambres de diferente diámetro y se midió en cada caso la deformación correspondiente. Con la segunda se deflectaron varillas mediante fuerzas tangenciales ABSTRACT We design and constructed a laboratory equipment of elasticity, with its respective guide for the correspondent elasticity practices in the level basic universitary physics. We developed an experimental analysis about the factors from which the elasticity materials depend. INTRODUCCION El estado que adopta la materia depende fundamentalmente de las fuerzas intermoleculares, que a la vez son función de su separación r. Para separaciones r0 ≈ 10 −10 m se tiene un sólido, debido a que a estas distancias los átomos o las moléculas se atraen con una fuerza recuperadora que como se observa en la figura 1 adquiere la forma F = − K (r − r ), semejante a la fuerza elástica ejercida por un resorte. 0 En r = r0 el átomo se halla en su posición de equilibrio. Para r< r0 la fuerza es repulsiva y aumenta rápidamente mostrando la imposibilidad del traslapamiento de las nubes electrónicas de los átomos. Para r > r0 la fuerza es de atracción. Las fuerzas restauradoras que mantienen a los átomos en los sólidos les dan poca libertad de movimiento generando una estructura tridimensional de equilibrio estable conocida como red cristalina, que depende de las fuerzas entre los átomos o moléculas, al igual que de su forma y orientación. Las constantes efectivas de los "Resortes" son 460 REVISTA COLOMBIANA DE FISICA, VOL. 33, No. 2, 2001 altas, por lo que se requiere de una gran fuerza para variar la distancia interatómica. Esto explica la rigidez de los materiales. Figura No.1 Variación de las fuerzas intermoleculares F con su separación r Las propiedades elásticas de los sólidos también se pueden explicar en función de los parámetros que se observan a una escala macroscópica. Dependiendo de la forma como se aplique una fuerza a un cuerpo, este experimentará una pequeña deformación aparentemente imperceptible. Los sólidos se resisten a estas deformaciones ejerciendo fuerzas de oposición proporcionales a las mismas. Una fuerza actuando perpendicularmente a una superficie de área A de un cuerpo producirá en él una compresión figura 2(a) o un estiramiento figura 2(b). En ambos casos el esfuerzo σ = F A es proporcional a la deformación ∈= ∆L L , siendo Y la constante de proporcionalidad conocida como el modulo de Young que caracteriza a cada uno de los materiales. Figura No.2 Representación microscópica de los átomos de un sólido sometido a una fuerza horizontal (a) de compresión (b) de tracción y (c) de corte. Cuando la fuerza es paralela a la superficie, las capas atómicas se desplazan como en la figura 2(c), siendo ∆L el desplazamiento de la última capa con respecto a su posición de equilibrio. Aquí σ = G ∈ donde G es él modulo de elasticidad a cortante. Para todo sólido, a partir de un determinado esfuerzo se deja de cumplir la proporcionalidad directa entre esfuerzo y deformación; se ha alcanzado el límite elástico del material. Una vez suspendido el esfuerzo, el cuerpo quedará deformado, no recuperará sus dimensiones originales. Al continuar el incremento del esfuerzo, se llegará finalmente al punto de ruptura del material. 461 REVISTA COLOMBIANA DE FISICA, VOL. 33, No. 2. 2001 PROCEDIMIENTO Y ANALISIS Se diseñaron y construyeron dos máquinas mecánicas para el estudio experimental de las propiedades elásticas de los materiales, una de tensión y la otra de corte. La primera consta de una estructura de hierro (figura 3), en donde en un extremo se fija la muestra a tensionar, mientras que en el otro va el soporte de una rueda y un trinquete, el cual va unido por medio de un tornillo de paso 0,8mm. a la base de un dinamómetro que registra fuerzas entre 0 y 50 kg-f donde se fija el otro extremo de la muestra. Su base se desplaza, sobre un riel, lo que se deforme el alambre de muestra, que es lo que rueda y trinquete desplazan al tornillo. La longitud del alambre se puede variar entre 20 y 50 cm cambiando de posición la base de la rueda y el trinquete. El extremo de una varilla fija a la base del dinamómetro presiona el vástago de un comparador de carátula, con el que se mide la variación de la longitud del alambre. Figura No.3 Máquina para el análisis experimental de los materiales sometidos a esfuerzos de tensión. Como experimento, se sometieron alambres de diferente material, longitud y sección transversal a incrementos graduales de tensión, midiendo en cada caso el correspondiente alargamiento. Algunos de los datos obtenidos mediante este método se muestran en la figura 4. ALAMBRES BAJO TENSION 450 400 Esfuerzo (MPa) 350 300 250 Hierro 200 Aluminio 150 Cobre 100 50 0 0 2 4 6 8 10 Deformación (x10-3 ) 12 14 16 Figura No.4 Curvas de esfuerzo σ contra deformación ε para un alambre de hierro, uno de cobre y uno de aluminio 462 REVISTA COLOMBIANA DE FISICA, VOL. 33, No. 2, 2001 En la figura 4 se observa que el comportamiento de las muestras sometidas a tensión es similar: un intervalo donde la curva esfuerzo-deformación es lineal, cumpliéndose la ley de Hooke, seguido de otro, en el que la pendiente experimenta una notable disminución, donde para pequeñas variaciones de esfuerzo se observa un gran incremento en la deformación, el "esfuerzo de fluencia", a partir del cual el material no recupera su longitud original, entra a la zona de plasticidad y continúa expandiéndose hasta su fractura para el esfuerzo último. La tabla 1 muestra los valores experimentales y los teóricos de estos esfuerzos (en Mpa) para cada una de las muestras. Los valores teóricos se encuentran dentro de un intervalo, ya que estos dependen de factores como la pureza del material, del tipo de aleación, etc. Tabla No.1 valores experimentales y teoricos del esfuerzo de Fluencia MATERIAL Aluminio Cobre Hierro Esf. De fluen. (Exp) 122 75 147 Esf. de fluen. (Teo) 35-500 55-330 120-290 Esf. Ultimo (Exp.) 220 300 400 Esf. Ultimo (teo.) 100-550 230-380 69-480 Para hallar él modulo de Young E de algunos materiales, se graficaron los intervalos donde la curva esfuerzo-deformación es lineal, y su pendiente, la razón entre el esfuerzo y la deformación, indica el modulo de Young del material. La figura 5 muestra los resultados obtenidos con alambres de hierro, cobre y aluminio. MODULODE ELASTICIDAD(E) Esfuerzo (MPa) 800 600 400 200 0 -200 -400 -600 Aluminio(y=72,98x) Cobre(y=121,55x) Hierro(y=92,31x) 0 5 10 15 20 25 Deformación (x10-3) 30 Figura No.5 Intervalos donde existe proporción directa entre material sometidas a tensión. 35 40 σ y ∈ para muestras de alambre de diferente Los valores experimentales y los "intervalos" de los teóricos del modulo de Young (en Gpa), de los materiales mostrados en la figura 5, se dan en la tabla 2. Tabla No.2 MATERIAL Aluminio Cobre Hierro Mod. De Young (Exp.) 73 122 92 Mod. De Young (Teo.) 70-79 110-120 83-170 La máquina de corte, mostrada en la figura 6, consta de una estructura de hierro en forma de L, en donde en un riel horizontal de 20 Cm de longitud, se desplaza una base 463 REVISTA COLOMBIANA DE FISICA, VOL. 33, No. 2. 2001 unida al extremo de una mordaza ubicada en posición vertical, con el fin de permitir la variación de la longitud de la varilla a deflectar. Un dinamómetro que registra fuerzas entre 0 y 12 Kg-f, va unido en su parte inferior al otro extremo de la mordaza y en su parte superior, al extremo de la varilla de muestra ubicada en posición horizontal y fija a la vertical de la estructura en L. Al girar la mordaza, su longitud se reduce ocasionando la acción de una fuerza sobre la varilla de muestra, y su correspondiente deflexión, medida con un comparador de carátula. Figura No.6 Máquina para el análisis experimental de los materiales sometidos a esfuerzos cortantes. Como experimento se deflectaron varillas de diferente material, longitud y sección transversal, midiendo la deformación correspondiente a cada esfuerzo aplicado. Los datos obtenidos mediante este método se muestran en la figura 7. En todas las gráficas se observa una proporcionalidad directa entre el esfuerzo y la deformación, donde la relación entre estas dos es él modulo de elasticidad a cortante de cada material. La tabla 3 muestra los valores experimentales y los "intervalos" teóricos para dicho modulo (en Gpa), de los materiales utilizados en el experimento. Como se puede observar, los valores obtenidos experimentalmente se encuentran dentro del intervalo del módulo de elasticidad a cortante que figura para las diferentes aleaciones de estos elementos. 464 REVISTA COLOMBIANA DE FISICA, VOL. 33, No. 2, 2001 VARILLAS BAJO ESFUERZO CORTANTE 5 y = 76,815x 4,5 4 y = 47,889x Esfuerzo (MPa) 3,5 3 y = 34,17x y = 28,757x 2,5 2 Cobre Aluminio Hierro Acero 1,5 1 0,5 0 0 0,01 0,02 Figura No.7 Gráficas de Tabla No.3 MATERIAL Aluminio Cobre Hierro Acero 0,03 σ 0,04 0,05 Deformación (x10-3 ) contra 0,06 0,07 0,08 0,09 ∈ para varillas sometidas a esfuerzos cortantes Mod. De Elast. A Cortante (Exp.) 29 34 48 77 Mod. De Elast. A Cortante (Teó.) 26-30 40-47 32-69 75-80 CONCLUSIONES Los resultados obtenidos con las "rudimentarias" máquinas de elasticidad construidas, son bastante aceptables ya que permitieron la observación del comportamiento de los materiales sometidos a fuerzas axiales y tangenciales, y la determinación de los módulos de elasticidad de Young y de Corte de diversos materiales. Además de los posibles errores en las medidas, debido a que los elementos de medición no son los más recomendables, existen otros factores como la utilización de materiales usados comúnmente en la industria, caracterizados por la falta de pureza, y en los que se desconoce su porcentaje en la aleación. AGRADECIMIENTOS A los doctores Henry Mateus y Jaime Londoño, directivos de la universidad F.I.T. , por su valoración y apoyo a la investigación. A los estudiantes Elizahín Galeano, Diana Pinzón, Alfredo Hernandez, Javier Díaz y Henry Barrera, por su colaboración en la construcción de las máquinas y en las mediciones. REFERENCIAS 1. S. P. Timoshenko y J. N. Goodier. Theory fo Elasticity. Third Edition. 1970. McGraw-Hill. J. M. Gere y S. P. Timoshenko. Mecánica de Materiales. Segunda Edición. 1996. Grupo 465