aqui. - Cenidet
Anuncio

CENTRO NACIONAL DE INVESTIGACIÓN
Y DESARROLLO TECNOLÓGICO
cenidet
CONTROL NEURODIFUSO MULTIVARIABLE APLICADO
AL CONTROL DE VELOCIDAD, POTENCIA Y TEMPERATURA
DE GASES DE ESCAPE DE UNA UNIDAD TURBOGAS
T
E
S
I
S
PARA OBTENER EL GRADO DE:
MAESTRO EN CIENCIAS EN
INGENIERIA
ELECTRÓNICA
P R E S E N T A:
ING. VICTOR OCTAVIO SEGURA OZUNA
DIRECTOR DE TESIS:
DR. CARLOS SALVADOR DE LARA JAYME
CO-DIRECTOR DE TESIS:
DR. VICTOR MANUEL ALVARADO MARTINEZ
CUERNAVACA, MORELOS, MÉXICO.
NOVIEMBRE 2004
RESUMEN
La demanda de energía eléctrica en México ha obligado al sector eléctrico a estar en
una búsqueda constante de métodos y sistemas que, entre otros objetivos, mejoren
continuamente la operación de las centrales generadoras de energía eléctrica. Como parte
de su misión, el Instituto de Investigaciones Eléctricas (IIE) ha promovido y apoyado la
investigación aplicada y el desarrollo tecnológico para mejorar los índices de seguridad,
disponibilidad, confiabilidad, eficiencia y durabilidad de centrales generadoras mediante el
desarrollo y la implantación de grandes sistemas digitales de información y control.
En la actualidad, dentro del esquema de generación de energía eléctrica, las
unidades turbogas (UTG) representan 7% de la generación del sector eléctrico nacional [1].
Estas unidades se han convertido en el modo dominante de la nueva generación eléctrica
en los EE.UU, ya sea en ciclo simple o combinado. Lo anterior, es atribuible al menor costo
de instalación por kilowatt generado, a los programas de construcción más cortos, a bajos
niveles de emisión de contaminantes y costos de operación competitivos.
El sistema de control de las unidades turbogas está basado en algoritmos de control
convencionales del tipo PI [2]. Este esquema de control es destinado para tareas de
regulación y rechazo a perturbaciones, y no para seguimiento de puntos de referencia. Los
controladores actúan todos sobre una sóla válvula de control, lo cual representa una fuerte
interacción entre los mismos, por ejemplo un ajuste en los parámetros del algoritmo del PI
digital de temperatura, puede mejorar su desempeño pero también puede afectar el
desempeño del control de velocidad o el de potencia.
La turbina de gas presenta un comportamiento no lineal y variante en el tiempo,
principalmente en la etapa de arranque donde se presentan varios disturbios importantes.
Actualmente, los controladores utilizados en los esquemas de control de las turbinas son
lineales, los cuales son sintonizados para un punto de operación específico y son
conservados así por tiempo indefinido.
En esta tesis se presenta la formulación de un controlador prealimentado
multivariable, diseñado con la combinación de las tecnologías de lógica difusa y redes
neuronales con el propósito de mejorar el control de velocidad, potencia y temperatura de la
UTG. Este control propuesto es usado en conjunción con el esquema de control
convencional de la UTG existente, para integrar una estrategia de control híbrida
prealimentada. El control prealimentado está compuesto por un sistema de inferencia difuso
de múltiples entradas y una sóla salida diseñado con datos de entrada y salida de la planta.
El controlador retroalimentado está compuesto por controladores tipo PI convencionales en
este tipo de unidades.
Con esta estrategia, el controlador prealimentado provee una mayor contribución en
la señal de control disminuyendo el esfuerzo de control de los controladores PI
convencionales y la fuerte interacción que existe entre ellos. Los controladores PI
retroalimentados aportan una menor señal de control utilizada para ajustes finos en la señal
de control.
SUMMARY
The electric power demand in Mexico has forced to the electric sector to be in a
constant search of methods and systems that, among other objectives, improve the
operation of the generating power stations of electric power continually. As part of their
mission, the Electrical Research Institute (IIE) it has promoted and leaning the applied
research and the technological development to improve the indexes of security, readiness,
dependability, efficiency and durability of central generating by means of the development
and the installation of big digital systems of information and control.
At the present time, inside the scheme of electric power generation, the gas turbine
(UTG) represent 7% of the generation of the national electric sector [1]. These units have
become the dominant way of the new electric generation in the U.S, either in simple cycle
or combined. The above-mentioned, is attributable at less installation cost for generated
kilowatt, to the shortest construction programs, at first floor levels of emission of pollutants
and competitive operation costs.
The control system of the gas turbine is based on conventional control algorithms of
the type PI [2]. This control scheme is dedicated for regulation tasks and rejection to
interferences, and it doesn't stop pursuit of reference points. The controllers act all on a
control valve, that which represents a strong interaction among the same ones, for example
an adjustment in the parameters of the algorithm of the digital PI of temperature, it can
improve their acting but it can also affect the acting of the speed control or that of power.
The gas turbine presents a non lineal behavior and variant in the time, mainly in the
starting stage where several important disturbances are presented. At the moment, the
controllers used in the scheme of control of the turbines are lineal, which are syntonized for
a specific operation point and they are conserved this way by indefinite time.
In this thesis the formulation of a controller feedback multivariable is presented,
designed with the combination of the technologies of fuzzy logic and neural networks with
the purpose of improving the control of speed, power and temperature of the UTG. This
proposed control is used in conjunction with the scheme of conventional control of the
existent UTG, to integrate a strategy of control hybrid feedback. The control feedback is
compound for a fuzzy inference system of multiple entrances and a left exit designed with
entrance data and exit of the plant. The controller feedforward is compound for
conventional controllers type PI in this type of units.
With this strategy, the controller feedback provides a bigger contribution in the
control sign the effort of the conventional controllers' PI control and the strong interaction
that it exists among them diminishing. The controllers PI feedforward contribute a smaller
control sign used for fine adjustments in the control sign.
INDICE
LISTA DE TABLAS ------------------------------------------------------------------------- iii
LISTA DE FIGURAS ------------------------------------------------------------------------- iii
LISTA DE ABREVIATURAS --------------------------------------------------------------- vi
INTRODUCCIÓN
Antecedentes ------------------------------------------------------------------------------------- 1
Estado del arte ----------------------------------------------------------------------------------- 3
Justificación ------------------------------------------------------------------------------------ 4
Planteamiento del problema a solucionar --------------------------------------------------- 5
Objetivo
----------------------------------------------------------------------------------- 5
Alcance
----------------------------------------------------------------------------------- 6
Aportaciones-------------------------------------------------------------------------------------- 6
Organización ------------------------------------------------------------------------------------ 6
CAPITULO 1
UNIDAD TURBOGAS
1.1
1.2
1.3
1.4
1.5
Introducción ----------------------------------------------------------------------------- 8
Ciclo de trabajo de una turbina de gas ----------------------------------------------- 9
Transformaciones de energía en una central turbogas ----------------------------- 10
Operación típica de una unidad turbogas -------------------------------------------- 11
Componentes principales de una unidad turbogas -------------------------------- 12
1.5.1
Compresor ------------------------------------------------------------------- 12
1.5.2
Cámara de combustión ------------------------------------------------------ 14
1.5.3
Turbina ------------------------------------------------------------------------ 15
1.5.4
Generador eléctrico --------------------------------------------------------- 15
1.5.5
Equipo auxiliar motor de arranque --------------------------------------- 16
1.5.6
Equipo del sistema de combustible --------------------------------------- 16
1.6 Ecuaciones principales que rigen el comportamiento de la UTG modelo
GE-5001 ---------------------------------------------------------------------------------- 17
1.6.1
Datos de operación de la TG-5001 ------------------------------------------ 22
1.7 Conclusiones -----------------------------------------------------------------------------23
CAPITULO 2
CONTROL CONVENCIONAL DE LA UNIDAD TURBOGAS
2.1 Introducción ---------------------------------------------------------------------------- 24
2.2 Evolución de los sistemas de control para unidades turbogas --------------------- 25
2.3 Requerimientos de control de una unidad turbogas -------------------------------- 25
2.3.1 Secuencia
----------------------------------------------------------- 26
2.3.2 Control de velocidad ------------------------------------------------------- 29
2.3.3 Control de potencia --------------------------------------------------------- 30
2.3.4 Control de temperatura ---------------------------------------------------- 31
2.4 Esquema actual de control (típico) -------------------------------------------------- 31
2.5 Comportamiento de control actual ------------------------------------------------- 33
2.6 Problemática del control actual ------------------------------------------------------ 35
i
2.7
Conclusiones -------------------------------------------------------------------------- 38
CAPITULO 3 CONTROL PREALIMENTADO NEURODIFUSO
MULTIVARIABLE
3.1. Introducción ------------------------------------------------------------------------- 40
3.2. Control prealimentado ------------------------------------------------------------- 41
3.3. Sistemas neurodifusos -------------------------------------------------------------- 44
3.3.1. Anfis ------------------------------------------------------------------------ 44
3.3.1.1.Arquitectura anfis ------------------------------------------------------ 44
3.4. Diseño del controlador neurodifuso multivariable ----------------------------- 47
3.5. Pruebas de CNMP con ajuste de los controladores ----------------------------- 55
3.6. Conclusiones ------------------------------------------------------------------------- 55
CAPITULO 4 EVALUACION Y ANALISIS DE RESULTADOS
4.1 Introducción----------------------------------------------------------------------------- 56
4.2 Ambiente de pruebas-------------------------------------------------------------------- 57
4.3 Pruebas del esquema propuesto vs esquema de control convencional --------- 57
4.3.1 Interacción entre los controladores --------------------------------------- 58
4.3.2 Evaluación del sistema de control mediante índices de
Comportamiento ------------------------------------------------------------ 67
4.3.3 Rechazo a disturbios ------------------------------------------------------- 71
4.4 Conclusiones ------------------------------------------------------------------------------ 74
CAPITULO 5 CONCLUSIONES
5.1
5.2
5.3
5.4
5.5
Introducción ------------------------------------------------------------------------Problemática -----------------------------------------------------------------------Conclusiones -----------------------------------------------------------------------Aportaciones -----------------------------------------------------------------------Trabajos futuros --------------------------------------------------------------------
75
76
76
76
77
APENDICE A AMBIENTE DE PRUEBA
A.1 Introducción ------------------------------------------------------------------------ 78
A.2 Sistema de prueba ----------------------------------------------------------------- 79
A.3 Modelo del sistema UTG ---------------------------------------------------------- 79
A.3.1 Bloque de control -------------------------------------------------------------- 80
A.3.2
Bloque del secuenciador ------------------------------------------------------ 81
A.3.3
Bloque de la UTG --------------------------------------------------------------82
A.4 Pruebas de simulación de la UTG ------------------------------------------------ 83
APENDICE B ANFISEDIT
B.1
B.2
Introducción ------------------------------------------------------------------------ 85
Procedimiento de diseño ---------------------------------------------------------- 86
ii
APENDICE C FUNDAMENTOS DE LÓGICA DIFUSA, REDES NEURONALES,
SISTEMAS NEURODIFUSOS Y ANFIS.
C.1
C.2
C.3
C.3.1
Lógica Difusa ------------------------------------------------------------------------- 90
Redes Neuronales
----------------------------------------------------------- 98
Sistemas Neurodifusos -------------------------------------------------------------105
ANFIS ...-------------------------------------------------------------------------------107
APENDICE D PUBLICACIÓN RVP-AI/2000
REFERENCIAS
---------------------- --------------113
--------------------------------------------------------------------------120
LISTA DE TABLAS
Tabla 1.1 Variables principales de la TG --------------------------------------------------17
Tabla 1.2 Nomenclatura -----------------------------------------------------------------------19
Tabla 3.1 Rangos reales de la variables vs rangos normalizados --------------------- 50
Tabla 3.2 Base de reglas del sistema neurodifuso -------------------------------------- 53
Tabla 4.1 Puntos de interacción entre los controladores -------------------------------- 60
Tabla 4.2 índices de error de la velocidad angular de la TG --------------------------- 68
Tabla 4.3 índices de error de la temperatura de gases de escape de la TG ----------- 69
Tabla 4.4 índices de error de la potencia generada por la TG ------------------------- 69
Tabla C.1 Funciones de pertenencia --------------------------------------------------------- 94
Tabla C.2 Comparativa entre las técnicas de RNA y lógica difusa ---------------------105
LISTA DE FIGURAS
Figura 0.1. Mapa de generación de energía eléctrica ------------------------------------ 2
Figura. 1.1 El ciclo Brayton (4 fases de operación) -------------------------------------- 9
Figura 1.2 Transformaciones de energía --------------------------------------------------- 11
Figura 1.3 Diagrama esquemático de una turbina de gas -------------------------------- 12
Figura 1.4. Diagrama presión-velocidad-temperatura del aire en el compresor ------- 13
Figura 1.5. Trayectoria del aire en una turbina de gas típica ------------------------------ 14
Figura 1.6 Sistema compresor-cámara de combustión-turbina de gas y sus variables- 17
Figura 2.1 Secuencia de arranque ----------------------------------------------------------- 26
Figura 2.2 Esquema actual de control de velocidad, potencia y temperatura------------ 32
Figura. 2.3 Diagrama a Bloques del Lazo de Control de Velocidad ------------------- 32
Figura 2.4 Gráfica de las respuestas de la turbina ---------------------------------------- 34
Figura 2.5 Gráfica de la velocidad de la turbina ante ajuste de los parámetros en el
PI de temperatura ---------------------------------------------------------------- 35
Figura 2.6 Gráfica del comportamiento de la temperatura de la turbina ante ajuste de los
parámetros en el PI de temperatura -------------------------------------------- 36
Figura 2.7 Gráfica de la potencia de la turbina ante ajuste de los parámetros en el PI
de temperatura -------------------------------------------------------------------- 36
Figura 2.8 Gráfica del error de la velocidad de la TG ----------------------------------- 37
Figura 2.9 Gráfica del error de la potencia de la turbina -------------------------------- 38
iii
Figura 3.1 Configuración del control de dos grados de libertad ------------------------ 41
Figura 3.2 Esquema de Control Propuesto aplicado al control de velocidad potencia
y temperatura de unidades turbogas ------------------------------------------ 43
Figura 3.3 Mecanismo de razonamiento para un sistema TSK --------------------------45
Figura 3.4 Diagrama del algoritmo ANFIS ------------------------------------------------ 45
Figura. 3.5 Obtención de los datos de entrenamiento ------------------------------------ 48
Figura 3.6 Mapeo lineal entre el dominio X de la variable física x y el universo de
discurso normalizado Y de la variable difusa y ------------------------------ 49
Figura. 3.7 Estructura del sistema neurodifuso -------------------------------------------- 51
Figura 3.8. Funciones de membresía tipo trapezoidal para cada entrada. a) de
velocidad, b) de potencia, c) de temperatura ---------------------------------- 52
Figura 3.9 Función de pertenencia trapezoidal ------------------------------------------ - 52
Figura 3.10 Implementación del sistema neurodifuso al esquema de control --------- 54
Figura 4.1 Gráfica de la velocidad angular de la TG.-------------------------------------- 58
Figura 4.2 Gráfica de la temperatura de los gases de escape de la TG. ---------------- 59
Figura 4.3 Gráfica de la potencia generada de la TG ------------------------------------- 59
Figura 4.4 Gráfica de la velocidad angular de la TG en el primer periodo de
control del PI de velocidad ------------------------------------------------------- 61
Figura 4.5 Gráfica de la velocidad angular de la TG en el segundo periodo de
control del PI de velocidad ----------------------------------------------------- 62
Figura 4.6 Gráfica de la TGE de la TG durante la etapa de arranque ------------------ 63
Figura 4.7 Gráfica de la TGE de la TG durante la etapa de generación --------------- 63
Figura 4.8 Gráfica del seguimiento de la referencia de potencia ----------------------- 64
Figura 4.9 Gráfica de la potencia máxima generada ------------------------------------- 65
Figura 4.10 Señales de control generadas por el esquema de control propuesto ----- 66
Figura 4.11 Señales de control de los esquemas de control ---------------------------- 66
Figura 4.12 índices de error IAE e ITAE de las respuestas de velocidad ------------- 68
Figura 4.13 índices de error IAE e ITAE de las respuestas de la TGE ----------------- 69
Figura 4.14 índices de error IAE e ITAE de las respuestas de la potencia generada - 69
Figura 4.15 Gráfica del error de seguimiento de la velocidad -------------------------- 70
Figura 4.16 Gráfica del error de seguimiento de la potencia --------------------------- 71
Figura 4.17 Respuestas de la potencia generada ante el disturbio --------------------- 72
Figura 4.18 Respuestas de la velocidad ante el disturbio ------------------------------- 73
Figura 4.19 Salida de los controladores ante rechazo a disturbio --------------------- 73
Figura A.1 Diagrama a bloques de la operación de la UTG --------------------------- 79
Figura A.2 Diagrama a Bloques del Sistema UTG -------------------------------------- 80
Figura A.3. Etapa de control de la UTG ---------------------------------------------------- 80
Figura A.4. Diagrama que muestra la parte del secuenciador lógica de la UTG ---- 81
Figura A.5 Diagrama interno de la UTG, válvulas de combustible, sangrado y
álabes guía, Compresor, Cámara de Combustión y Turbina. ------------- 82
Figura A.6 Graficas de las respuestas en la UTG ----------------------------------------- 84
Figura B.1 Datos de entrenamiento --------------------------------------------------------- 86
Figura B.2 selección de numero y tipo de funciones de membresía ------------------ 87
Figura B.3 Comportamiento del error durante el entrenamiento ---------------------- 88
Figura B.4 Verificación del entrenamiento del sistema neurodifuso ----------------- 89
Figura C.1 Funciones de pertenencia de tres conjuntos difusos para la velocidad de un
automóvil ---------------------------------------------------------------------------91
iv
Figura.C.2 Bloques funcionales del sistema difuso ----------------------------------------94
Figura C.3 Tipos de razonamiento difuso -------------------------------------------------- 98
Figura C.4 Diagrama de la Red Neuronal Artificial. --------------------------------------101
Figura C.5 arquitectura de una red de 2 entradas, y 1 salida (propagación)------------107
Figura C.6 arquitectura de una red de 2 entradas, y 1 salida (retro.propagación) -----109
Figura C.7 Función de membresía tipo triangular. ----------------------------------------111
v
Lista de Abreviaciones
ANFIS
Adaptive Network based Fuzzy Inference System
ARIC
Aproximate Reasoning based Intelligent Control
c.a
Corriente alterna.
CD
Conjunto Difuso
CFE
Comisión Federal de Electricidad.
CGCC
Centrales de Generación de Ciclo Combinado ()
CNM
Controlador Neurodifuzo Multivariable
CNMP
Controlador Neurodifuzo Multivariable Prealimentado
CSV
Controlador Supervisor de Velocidad
CTG
Centrales Turbogas
DELTAet
Angulo de desfasamiento de campos magnéticos del generador.
Ecomp
Energía del compresor.
EE.UU
Estados Unidos de America
FALCON
Fuzzy Adaptive Learning Control Network
FP
Función de Pertenencia
FuNe
Fuzzy Network
Gaic
Flujo de aire que entra al compresor.
GARIC
Generalized Aproximate Reasoning based Intelligent Control
Gasang
Flujo que sale de las válvulas de sangrado.
Gasc
Flujo de aire que sale del compresor.
Gcgt
Flujo de combustible gas a la cámara de combustión.
Gct
Flujo total de combustible a la cámara de combustión.
GE
General Electric
Ggicct
Flujo de gases que entran a la cámara de combustión.
Ggit
Flujo de gases que salen de la cámara de combustión.
Gqclt
Flujo de combustible diesel a la cámara de combustión.
Hcct
Energía en la cámara de combustión.
Hgst
Energía a la salida de la turbina de gas.
IAE
Integral Absoluta del Erro
vi
Lista de Abreviaciones
IEEE
Instituto de Ingenieros Eléctricos y Electrónicos
IHM
Interfaz Hombre Maquina
IIE
Instituto de Investigaciones Eléctricas
IPG
Interruptor Principal del Generador
ITAE
Integral del Tiempo por el valor Absoluto del Error
LD
Lógica Difusa
MISO
Multiples entradas- simple salida
MW
Megawatts
NEFCON
Neuro Fuzzy Control
NNDFR
Neural Network Driven Fuzzy Reasoning
OMEGAt
Velocidad angular de la turbina.
OMEGAtr
Velocidad angular del generador.
PC
Computadora Personal
Pcct
Presión en la cámara de combustión.
PI
Proporcional Integral
PID
Proporcional Integral Derivativo
Piqg
Presión del combustible gas.
Piql
Presión del combustible diesel.
Pj
Presión atmosférica.
RN
Redes Neuronales
RNA
Redes Neuronales Artificiales
RPM
Revoluciones por minuto
RVP-AI
Reunión de Verano de Potencia, Aplicaciones Industriales
Tacct
Temperatura de entrada a la cámara de compresión.
TG
Turbinas de Gas
Tgcct
Temperatura en la cámara de combustión.
Tgst
Temperatura de gases que salen de la turbina.
Tsang
Temperatura del flujo de aire de sangrado.
TSK
Takagi Sugeno Kan
vii
Lista de Abreviaciones
UTG
Unidad Turbogas
VL
Variable Lingüística
Vol
Voltaje en terminales.
Wet
Energía eléctrica producida por el generador.
Wft
Fricción en la turbina de gas.
Xcgt
Apertura de la válvula de control de combustible gas.
Xqclt
Apertura de la válvula de control de combustible diesel.
viii
Introducción
Antecedentes.
La mayoría de las Centrales Generadoras de Energía Eléctrica que se encuentran
actualmente en servicio fueron instaladas en las décadas de los 60’s y 70’s. La década de
los 80’s se caracterizó principalmente por una baja actividad en la instalación de nuevas
centrales, en los 90’s se observó un notable incremento en la demanda, bajo un clima de
fuerte incertidumbre económica y con un bajo crecimiento en la capacidad instalada.
En la actualidad, la Comisión Federal de Electricidad (CFE) está preparada para la
reestructuración de acuerdo al Programa de desarrollo y reestructuración del sector de la
energía [3], en el cual se alienta la participación privada en la generación eléctrica y se
orienta a la inversión pública a mejorar y fortalecer la transmisión y distribución de
electricidad. De esta forma, la CFE avanza en la transición de un monopolio a un mercado
abierto donde haya competencia entre un mayor número de participantes.
La CFE también fortalece y amplía su infraestructura con la adopción de nuevas
tecnologías y el impulso a la investigación y desarrollo tecnológico del sector, incorpora
más calidad en sus procesos de producción disminuyendo también la afectación del medio
ambiente.
1
Introducción
El gas es actualmente la fuente que requiere de menor inversión de capital y la más
limpia para la obtención del fluido energético. La evolución mundial de los sistemas
eléctricos que utilizan gas es inevitable, pues se sabe que el costo de capital por MW
invertido en una planta de gas equivale a cerca de la mitad del costo de capital en una
planta convencional (por ejemplo una planta hidroeléctrica o una carboeléctrica)[3]. Debido
a esto la CFE se prepara para incrementar la utilización de gas en la generación de
electricidad, previendo que en pocos años se pasará de un 16 % a un 60 % en su consumo.
Otra de las estrategias adoptadas por la CFE para satisfacer la demanda de energía
eléctrica presenta un enfoque hacia la producción, a menor costo, de más energía eléctrica
con la capacidad instalada existente. Con respecto a esto, desde una perspectiva técnica, son
de vital importancia los problemas de extensión de la vida útil (duración del equipo) y el
mejoramiento del régimen térmico de las centrales (eficiencia de los procesos de
transformación de energía).
Como resultado del ambicioso programa de construcción de plantas generadoras de
energía eléctrica que el gobierno mexicano inició en 1998, para el año 2001 la CFE alcanzó
una capacidad instalada de generación cercana a 36 mil MW. La meta principal de la
empresa eléctrica nacional consiste en satisfacer la gran demanda de energía eléctrica que
requiere el crecimiento industrial del país, principalmente mediante centrales de generación
más flexibles, eficientes y rentables basadas en el uso del gas [4] .
En la actualidad, dentro del esquema de generación de energía eléctrica, las
unidades turbogas representan 7% de la generación del sector eléctrico nacional como lo
muestra la figura 0.1. Cada unidad cuenta con una capacidad nominal de generación de
hasta 24 MW. Sin embargo, la característica de rápida entrada en generación ha hecho de
éstas un equipo particularmente adecuado para satisfacer cargas pico o como fuentes de
energía de respaldo.
Turbogas 7%
Combustión
interna
0.4%
Ciclo combinado
17.8%
Hidroeléctrica 23.3%
Dual 6.1%
Carboeléctrica
6.3%
Nucleoélectrica 3.3%
Geotérmica y
eoélectrica 2.1%
Térmica
convencional
34.7%
Figura 0.1 Mapa de generación de energía eléctrica
2
Introducción
Este tipo de unidad se ha instalado en grandes centrales térmicas, nucleares o en
refinerías como fuentes primarias de energía. Las aplicaciones más exitosas de las unidades
turbogas se dan en las centrales generadoras del tipo ciclo combinado, en donde constituyen
el factor predominante para lograr los porcentajes más elevados de eficiencia entre todos
los tipos de centrales generadoras. Adicionalmente y debido a las ventajas que presentan en
cuanto a transportabilidad, tamaño, peso, adaptabilidad a una gran variedad de
combustibles (desde gas natural hasta petróleo crudo o residual), y gran facilidad para
responder a cargas pico, las unidades turbogas, operadas en ciclo abierto, son
universalmente utilizadas en las instalaciones del sector petrolero y en poblados de difícil
acceso con poca demanda y escasez de agua.
La demanda de energía eléctrica en México ha obligado al sector eléctrico a estar en
una búsqueda constante de métodos y sistemas que, entre otros objetivos, mejoren
continuamente la operación de las centrales generadoras de energía eléctrica. Como parte
de su misión, el Instituto de Investigaciones Eléctricas (IIE) ha promovido y apoyado la
investigación aplicada y el desarrollo tecnológico para mejorar los índices de seguridad,
disponibilidad, confiabilidad, eficiencia y durabilidad de centrales generadoras mediante el
desarrollo y la implantación de grandes sistemas digitales de información y control.
Estado del arte
La demanda de energía eléctrica ha obligado al sector eléctrico a estar en una
búsqueda constante de métodos y sistemas que, entre otros objetivos, mejoren
continuamente la operación de las centrales generadoras de energía eléctrica.
Influenciados por las experiencias logradas en proyectos de contrato para CFE, el
Instituto de Investigaciones Electricas ha desarrollado diversos proyectos de investigación
dirigidos a mejorar la operación de las centrales generadoras. Una de las líneas de
investigación desarrolladas para lograr este objetivo, es el diseño de sistemas de control
basados en técnicas de control inteligente. A continuación se mencionan algunos de los
proyectos desarrollados:
En1995 se realizó una aplicación de redes neuronales artificiales al control
supervisor de turbinas de gas [5]. En.1997 se desarrolló un controlador difuso de velocidad
en tiempo real para el arranque de la turbina de gas [6]. Posteriormente, este trabajo fue
extendido para abarcar el control de potencia generada [2]. En ambos casos los resultados
obtenidos fueron exitosos y constituyen una base sólida para la aplicación de controladores
difusos a una unidad turbogas real. Así mismo, se trató el problema de sintonización
mediante redes neuronales de los controladores convencionales y difusos [7]. Con el objeto
de consolidar la línea de desarrollo tecnológico de sistemas de control inteligente de
unidades generadoras tipo turbogas, se desarrolló un controlador híbrido neurodifuso retroprealimentado aplicado al control de velocidad y potencia para dicho tipo de unidad. Los
resultados logrados fueron a nivel simulación en PC y en plataforma industrial de
laboratorio [8]. Estos fueron alentadores, de manera tal que es importante continuar con
esta misma línea de investigación.
3
Introducción
Algunos estudios realizados por otras instituciones han explorado el esquema retroprealimentado basados en simulaciones, como un controlador prealimentado difuso
multivariable para una unidad termoeléctrica [9]. Así como también, han realizado el
desarrollo de controladores neurodifusos aplicados al control de turbinas de gas, estos
controladores fueron diseñados apoyándose con el uso de la herramienta de simulación
comercial Matlab [10].
Justificación
La importancia de trabajar con Turbinas de Gas (TG) radica en que se han
convertido en el modo dominante de la nueva generación eléctrica en los EE.UU, ya sea en
ciclo simple o combinado. Lo anterior, es atribuible al menor costo de instalación por
kilowatt generado, a los programas de construcción más cortos, a bajos niveles de emisión
de contaminantes y costos de operación competitivos. Avances recientes en las tecnologías
de TG y compresores han logrado que la eficiencia térmica se aproxime al 60% para las
Centrales de Generación de Ciclo Combinado (CGCC) basadas en gas [4].
Además, a diferencia de otros impulsores primarios, las turbinas de gas se
caracterizan principalmente por ocupar poco espacio en su instalación y gran simplicidad
de maniobra.
Las unidades turbogas operadas en ciclo abierto (centrales turbogas CTG),
conectadas a redes pequeñas o utilizadas en operación aislada, son muy susceptibles de
volverse inestables ante una perturbación severa, como las producidas por el arranque y
salida de grandes motores de inducción (de hasta 10 MW) típicos en los complejos
industriales; así como por cambios súbitos de carga de hasta 2 MW, lo que puede provocar
la salida de operación de la unidad y derivarse en pérdidas de producción y daños a terceros
equipos[11].
La aplicación de un controlador neurodifuso multivariable se justifica ya que el uso
de controladores independientes (control/supervisor) que operan sólo al actuar sobre una
válvula de control implica una interacción importante entre los controladores (de velocidad,
potencia y temperatura de gases de escape). Esta interacción puede considerarse en un solo
controlador multivariable de tipo MISO. Además, una alternativa para tratar esta
interacción y mejorar el desempeño de la unidad turbogas es el empleo de técnicas de
control inteligente.
El uso de controladores neurodifusos los cuales son no lineales han demostrado ser
una opción viable para controlar procesos que presentan un comportamiento no lineal y
variante en el tiempo como el de arranque de una turbina de gas, así como el desempeño de
dichos procesos.
De acuerdo a lo anterior, se deriva la importancia de realizar mejoras en cuanto a la
disponibilidad, efectividad y confiabilidad de este tipo de unidad de generación.
4
Introducción
Planteamiento del problema a solucionar
Las generadoras turbogas o turbogeneradores a gas (TG) son sistemas de alto riesgo
que operan a altas velocidades, temperaturas y presiones. Estas condiciones establecen
requerimientos muy estrictos para el sistema de control.
Típicamente la estrategia general de control utilizada para la operación de la UTG
consiste en la regulación de flujo de combustible. El núcleo del esquema de control está
formado básicamente por un circuito dual de control de velocidad y carga para la
regulación de flujo de combustible a través de una válvula de control, el cual es
supervisado por un control de temperatura.
El sistema de control de las unidades turbogas está basado en algoritmos de control
convencionales del tipo PI [2]. Este esquema de control es destinado para tareas de
regulación y rechazo a perturbaciones, y no para seguimiento de puntos de referencia. Los
controladores actúan todos sobre una sóla válvula de control, lo cual representa una fuerte
interacción entre los mismos, por ejemplo un ajuste en los parámetros del algoritmo del PI
digital de temperatura, puede mejorar su desempeño pero también puede afectar el
desempeño del control de velocidad o el de potencia.
La turbina de gas presenta un comportamiento no lineal y variante en el tiempo,
principalmente en la etapa de arranque donde se presentan varios disturbios importantes.
Actualmente, los controladores utilizados en los esquemas de control de las turbinas son
lineales, los cuales son sintonizados para un punto de operación específico y son
conservados así por tiempo indefinido.
Una alternativa para tratar esta interacción y mejorar el desempeño de la unidad
turbogas es el empleo de técnicas de control inteligente, adoptando un esquema
prealimentado tal como se menciona en el objetivo de esta propuesta.
Objetivo
Esta tesis tiene como objetivos:
•
Diseñar y desarrollar un sistema de control prealimentado neurodifuso multivariable
basado en técnicas de control inteligente, para su incorporación al sistema de control de
velocidad, potencia y temperatura de los gases de escape de una unidad turbogas.
•
Disminuir la afectación negativa sobre la señal de control, provocada por la
interacción de los controladores.
•
Mejorar el seguimiento de las trayectorias de referencia de la velocidad y la
potencia.
•
Obtener una mejor regulación de la temperatura.
5
Introducción
Alcance
El trabajo de tesis plantea el siguiente alcance:
•
El desarrollo y la integración del sistema neurodifuso multivariable se realizará
bajo el ambiente de programación Matlab/Simulink.
•
Revisar el modelo de la unidad turbogas y de su sistema de control en el ambiente
Simulink.
•
Validación por comparación del control prealimentado neurodifuso multivariable
contra el desempeño del sistema de control convencional basado en controladores tipo
PID.
Aportaciones.
El trabajo de tesis aporto el diseño y desarrollo de un esquema de control
prealimentado multivariable, basado en técnicas de control inteligente, el cual será aplicado
a procesos de generación.
El control neurodifuso multivariable supera algunas de las desventajas del control
convencional y satisface los requerimientos de operación.
El desarrollo de esta tesis ayudará a fortalecer la línea de investigación del grupo de
control de la Gerencia de Control e Instrumentación del IIE, sobre el diseño de
controladores para mejorar el desempeño de centrales generadoras de energía .
Se publicó el articulo “Control Neurodifuso Aplicado al Control de Velocidad,
Potencia y Temperatura de Unidades Turbogas” en la 17ª reunión de verano de potencia,
aplicaciones industriales y exposición industrial. (RVP-AI/2004), IEEE, Acapulco.
Guerrero (anexo D).
Organización.
El contenido de este trabajo de tesis esta conformado por 5 capitulos y 3 anexos,
mismos que se describen a continuación.
En el capítulo 1 se presenta el funcionamiento y descripción de las unidades
turbogas, las ecuaciones principales del modelo matemático que rigen su comportamiento,
así como la implementación del modelo en el ambiente gráfico Simulink .
En el capítulo 2 se exponen los requerimientos de control, la secuencia de operación
de la unidad turbogas, el esquema actual de control (comportamiento, ventajas y
desventajas) que opera en la unidad turbogas.
6
Introducción
En el capítulo 3, se describe el desarrollo de un controlador prealimentado
multivariable, se presenta el esquema de control propuesto, se describe la arquitectura
básica de las redes neuronales y del control difuso. Así como la combinación de ambas
técnicas de control para la formulación del control híbrido-neurodifuso.
En el capítulo 4 se muestra el desarrollo de diferentes controladores neurodifusos,
así como los resultados obtenidos con estos, de igual manera se compara el comportamiento
del esquema de control híbrido neurodifuso contra el esquema de control convencional,
aplicando criterios de error y rechazo a disturbios.
En el capítulo 5 se establecen las conclusiones y los logros obtenidos en el presente
trabajo de tesis. También se proporcionan algunas sugerencias de posibles trabajos a futuro
relacionados con la presente investigación.
En el apéndice A se describe el sistema para desarrollo y validación de algoritmos
de control para turbinas de gas.
El apéndice B muestra el procedimiento para el diseño de sistemas neurodifusos
utilizando la herramienta Anfisedit de Matlab.
El apéndice C presenta los conceptos fundamentos sobre lógica difusa, control
difuso, redes neuronales, sistemas neurodifusos y algoritmos de aprendizaje de ANFIS.
tesis.
El apéndice D finalmente presenta el articulo publicado, producto de este trabajo de
7
CAPITULO 1
Unidad Turbogas
Unidad Turbogas
1.1
Introducción.
Este capítulo explica el funcionamiento de una turbina de gas típica, se detalla el
principio de operación el cual esta basado en el ciclo Brayton, además presenta la
descripción de los componentes principales que la integran y la operación de cada uno de
ellos. también se presentan las transformaciones de energía que tienen lugar en una central
turbogas, por ultimo se presentan las variables y ecuaciones principales del modelo
matemático que rigen el comportamiento de la turbina de gas.
8
CAPITULO 1
1.2
Unidad Turbogas
Ciclo de trabajo de la turbina de gas
La turbina de gas es una máquina de combustión interna que transforma la energía
química de una fuente combustible en potencia mecánica útil, es decir, en energía mecánica
rotatoria.
En general, las turbinas de gas se basan en cuatro fases de operación (ciclo Brayton)
y cuatro componentes principales (figura 1.1), que funcionan simultáneamente y
continuamente, para producir potencia mecánica los cuales se describen mas adelante.
La operación de una turbina de gas de ciclo simple puede explicarse mediante el
ciclo Brayton, el cual consiste de cuatro fases: compresión, adición de calor, expansión y
expulsión del calor. La cantidad de trabajo que se produce durante el ciclo, está relacionada
con la cantidad de calor que produce el combustible y que señala la cantidad de trabajo que
producirá la turbina de gas. Debido a que la cantidad de calor se indica por la temperatura y
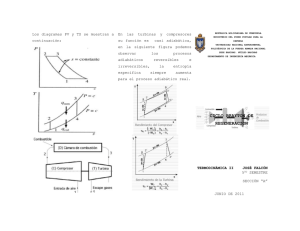
la entropía; el ciclo Brayton se aprecia en la figura. 1.1 b).
Combustible
Camara
comb.
2
Compresor
1
3
Turbina
Generador
4
Gases
calientes
Aire
a)
b)
Figura. 1.1 a) Componentes principales. b) El ciclo Brayton (4 fases de operación)
Examinando el ciclo Brayton [12], se observa que el punto 1 describe la temperatura
y presión del aire ambiente. Estas condiciones ambientales tienen un efecto significante en
el trabajo de salida y en la eficiencia de ciclo de la turbina. La turbina de gas obtiene aire a
estas condiciones y lo comprime hasta cierta presión; este aumento de la presión del aire
ocasiona un incremento en su temperatura. En la figura 1.1 b) se aprecia el cambio del
punto 1 al punto 2. Nótese que la trayectoria es en forma vertical, la razón es que el proceso
de compresión ideal es isoentrópico (no hay variación en el grado de orden o desorden
molecular del gas), esto significa que no existe transferencia de calor con el aire. Por lo
9
CAPITULO 1
Unidad Turbogas
tanto, aun cuando la temperatura del gas puede cambiar en el proceso, su entropía no lo
hará.
Después de la compresión el aire pasa al sistema de combustión donde se añade
calor. El aire se mezcla con el combustible y la mezcla se enciende causando un incremento
muy grande en la temperatura. Esto se realiza a presión constante, así que el proceso se
ilustra en la figura como un cambio del punto 2 al 3.
Cuando entra la mezcla a la sección de la turbina, su presión incide (otra vez
isoentrópicamente, es decir sin variación) contra los alabes de la turbina, ocasionando que
su eje gire y el gas continúa expandiéndose hasta que regresa a la presión ambiente. Este
proceso es mostrado en la figura en el cambio del punto 3 al punto 4.
Debido a las curvaturas de las líneas de presión constante, la temperatura de la
mezcla todavía es alta comparada con la temperatura ambiente, lo que indica que todavía
existe una cantidad significante de calor. Este calor es rechazado cuando la mezcla se enfría
a la temperatura ambiente; trayectoria del punto 4 al punto 1.
Examinando el ciclo gráficamente, la ignición y el calor añadido por el combustible
se representan por el área bajo la curva, entre los puntos 2 y 3. El calor rechazado a la
atmósfera se representa por el área bajo la curva entre los puntos 1 y 4. El área contenida
por la superficie sombreada es la potencia de salida y la proporción de ésta al área total bajo
los puntos 2 y 3 es la eficiencia térmica.
El ciclo real de la turbina de gas difiere poco del caso ideal; la diferencia principal
entre el ciclo Brayton ideal y el ciclo real es que tanto los procesos de compresión como el
de expansión no son isoentrópicos, además de que existen diversas clases de perdidas
mecánicas.
1.3
Transformaciones de energía en una central turbogas.
En una central generadora, la energía eléctrica se produce como resultado de una
serie de transformaciones que se inician a partir de alguna fuente de energía disponible.
Para el caso particular de una Central Turbogas, las transformaciones de energía que
ocurren en este tipo de central se muestran en la figura 1.2. La fuente de energía primaria
es un combustible, generalmente gas natural o diesel. La energía se encuentra almacenada
en el combustible de acuerdo a su composición química y se libera haciendo que se
produzca una reacción química por medio del proceso de combustión.
Al producirse la combustión, se tiene la primera transformación de energía, ya que
la energía química del combustible se transforma en energía calorífica en la flama y en los
gases calientes producto de la combustión. Este proceso se realiza en la cámara de
combustión de la turbina de gas.
Los gases calientes producto de la combustión se envían a una turbina, en donde se
expanden y desarrollan trabajo mecánico. De esta manera, la energía calorífica producida
por la combustión, es transformada en energía mecánica rotatoria por la turbina, la cual gira
debido a la energía cinética de los gases en expansión.
10
CAPITULO 1
Unidad Turbogas
Combustibles
Energia quimica
Combustión
Energia calorifica
Flujo de gases
Energia cinetica
movimineto de la turbina
Energia mecánica
Movimiento del generador
Energia eléctrica
Figura 1.2 Transformaciones de energía.
La turbina de gas se encuentra acoplada mecánicamente a un generador eléctrico y,
mediante éste, la energía mecánica producida puede ser transformada finalmente en energía
eléctrica.
1.4
Operación típica de una unidad turbogas
Los componentes principales de una unidad turbogas (UTG) son:
a) La turbina de gas, compuesta por el compresor, la cámara de combustión y la turbina
propiamente dicha.
b) El generador eléctrico.
La representación esquemática de una UTG se puede observar en la figura 1.3, en la
cual se muestra una turbina de gas de un solo eje y de ciclo abierto, acoplada a un
generador eléctrico. Mediante esta figura, se puede conocer la operación básica de una
UTG. Un compresor gira e introduce aire del medio ambiente que posteriormente se
comprime hasta un valor aproximado de 10 Atmósferas y se envía a la cámara de
combustión. De esta manera se proporciona el suministro de oxígeno necesario para poder
quemar el combustible. Aunque en esta etapa aún no se ha agregado calor, la temperatura
del aire se incrementa debido a la compresión. En la cámara de combustión, el aire
comprimido se combina con el combustible alimentado y, con la ayuda de una bujía de
11
CAPITULO 1
Unidad Turbogas
ignición, se produce la combustión, que provoca un incremento substancial de la
temperatura. Los gases producto de la combustión son enviados a la turbina de gas, en
donde se expanden y desarrollan trabajo mecánico que se aprovecha para impulsar un
generador eléctrico y producir energía eléctrica. [13]
Combustible
Gas ó Diesel
Aire
comprimido
CÁMARA DE
COMBUSTIÓN
Gases
calientes
COMPRESOR
TURBINA
Gases de
escape
GENERADOR
Aire
atmosférico
Figura 1.3 Diagrama esquemático de una turbina de gas
Durante la expansión de los gases, su temperatura y presión se reducen
continuamente mientras realizan trabajo en los álabes de la turbina. Después de realizar
trabajo, los gases de escape, aún calientes, son enviados a la atmósfera, en donde se enfrían
a temperatura ambiente.
1.5
Componentes principales de una unidad turbogas
1.5.1
Compresor
El primer componente en el ciclo de operación de la turbina de gas es el compresor,
el cual es un elemento mecánico rotatorio que tiene como función comprimir el fluido de
trabajo (aire).
Para que la turbina de gas pueda tener alguna aplicación práctica, se necesita de un
gran volumen de aire a alta presión con el propósito de quemar suficiente combustible en la
cámara de combustión. Esto se obtiene comprimiendo el aire a una presión deseada por
medio de un compresor de flujo axial.
Para obtener la presión requerida, los compresores de flujo axial están constituidos
por varias etapas, en donde, en cada una de ellas, el aire se acelera y se comprime. Cada
etapa del compresor axial consiste en una serie de álabes móviles (giratorios) seguidos por
12
CAPITULO 1
Unidad Turbogas
un conjunto de álabes fijos. En cada etapa, los álabes móviles aceleran el aire y los álabes
estacionarios convierten la energía cinética del aire en un incremento de presión. Por lo
tanto, incrementando la velocidad del aire por cada serie de álabes móviles y convirtiendo
esta velocidad en aumentos de presión por medio de los álabes fijos, se obtiene la fuente de
aire a alta presión necesitado para la combustión. Los compresores axiales utilizados en
UTG's normalmente tienen de 15 a 20 etapas. La figura 1.4 muestra el diagrama de presión,
velocidad y temperatura del aire a lo largo de un compresor axial. Como puede verse, la
presión y la temperatura aumentan, mientras que la velocidad apenas varía.
Cada etapa del compresor tiene ciertas características de flujo de aire que son
diferentes a las demás etapas. Los parámetros que determinan estas características son el
flujo másico, la razón de presión y la velocidad rotacional. Las etapas del compresor están
diseñadas para producir un flujo de aire dado relacionado con un cierto incremento de
presión. Si algún suceso altera la relación entre razón de presión, velocidad rotacional y
flujo másico, el aire no fluirá suavemente por los álabes estacionarios, y en cambio, creará
turbulencias. Esto ocasionará un "atascamiento" en los álabes fijos que impedirá que el aire
fluya hacia la siguiente etapa. Como resultado, el aire también se "estanca" en las etapas
precedentes. Si este proceso continua hasta que todas las etapas están "atascadas", el flujo
de aire podría invertirse y moverse violentamente causando un ruido estrepitoso y,
seguramente, un daño considerable a los álabes del compresor. Este fenómeno de
inestabilidad es conocido como "surge" del compresor y debe prevenirse para evitar
condiciones anormales de operación.
Álabes
móvile
Álabes
fijos
Álabes Álabes
móvile fijos
Álabes Álabes
movile fijos
Velocidad
Presión
Temperatura
del
Compresor
Figura 1.4. Diagrama presión-velocidad-temperatura del aire en el compresor.
13
CAPITULO 1
1.5.2
Unidad Turbogas
Cámara de combustión
Es un elemento que consiste de compartimientos (canastas) en los cuales se quema
combustible y se añade energía térmica al fluido de trabajo. El propósito de la cámara de
combustión es, por lo tanto, agregar calor al aire comprimido.
La cantidad de trabajo que puede ser realizado por una turbina de gas ideal, es decir,
sin calor agregado y sin pérdidas de energía, es exactamente igual a la cantidad de trabajo
hecho por el compresor para comprimir el aire. En otras palabras, la máquina podría girar
por sí misma. Las turbinas de gas, sin embargo, tienen pérdidas de potencia considerables
en el compresor y en la turbina misma. En consecuencia, es necesario agregar energía al
fluido de trabajo para obtener una turbina de gas útil y práctica. El calentamiento del aire
incrementa la presión, el aire se expande y esta energía mueve la combinación turbinacompresor, así como también proporciona potencia para el generador eléctrico.
El aire a alta presión proveniente del compresor entra a los combustores, localizados
generalmente en una sección entre el compresor y la turbina (figura 1.5). El combustible se
alimenta por medio de toberas y se mezcla con el aire comprimido, necesario para producir
la combustión. El aire entra a la zona de combustión a través de perforaciones en el
revestimiento protector de los combustores, que protege al metal de la carcaza de la turbina
contra las radiaciones intensivas producidas por la combustión. La combustión comienza
con una mezcla parcial de combustible y aire, y continúa a lo largo del combustor, mientras
se agrega aire adicional para completar la combustión y enfriar los gases. Normalmente,
solamente del 20% al 30% del aire comprimido se utiliza para quemar el combustible,
mientras que el resto fluye entre los combustores y la carcaza de la máquina para propósitos
de enfriamiento. La mayoría de las turbinas de gas tienen una serie de combustores
instalados alrededor del eje; de esta manera, las temperaturas y los esfuerzos en los álabes
de la turbina se distribuyen uniformemente.
Figura 1.5. Trayectoria del aire en una turbina de gas típica.
14
CAPITULO 1
1.5.3
Unidad Turbogas
Turbina
La turbina es un componente mecánico rotatorio que produce energía mecánica por
la acción de un fluido de trabajo. La turbina convierte la energía del flujo de los gases
calientes en energía mecánica rotacional por medio del proceso de expansión de los gases.
Normalmente está constituida de 3 a 5 etapas (para el caso de unidades de eje
simple). Cada etapa consiste de un conjunto de toberas fijas seguido por una serie de
paletas o alabes móviles. Los gases se expanden en las toberas fijas y se obtiene una
corriente de gases a alta velocidad; estos gases actúan contra el conjunto de paletas móviles
y proporcionan un par al rotor de la turbina. Aproximadamente, dos terceras partes de la
potencia de la turbina se utiliza para mover el compresor axial, mientras que el resto se
emplea en la generación de potencia eléctrica.
Debido a las elevadas temperaturas de gas en la entrada de la turbina, las primeras
etapas deben ser enfriadas para obtener un período de vida útil económicamente justificable
del empaletado. El enfriamiento se proporciona normalmente por medio de una parte del
aire suministrado por el compresor. El rotor mismo y el estator también deben ser
protegidos contra las altas temperaturas. Algunas turbinas también emplean enfriamiento en
algunas etapas (Turbinas de Gas con Regeneración e intercambiador de calor), pero
generalmente las turbinas no necesitan enfriarse debido a que la temperatura de los gases se
reduce mientras éstos se expanden a través de la turbina.
1.5.4
Generador eléctrico
El generador eléctrico es una máquina síncrona que convierte la energía mecánica
de la turbina en energía eléctrica de c.a. de voltaje y frecuencia específicos.
En general, el principio de operación de las máquinas eléctricas está basado en el
fenómeno de inducción electromagnética y, en particular, para el caso del generador
síncrono consiste en la generación de una fuerza electromotriz en un sistema de
conductores estacionarios que son cortados por las líneas de flujo de un campo magnético
giratorio. Para tal fin, el generador tiene un sistema inductor, destinado a crear el campo
magnético, y un sistema de inducido, en el cual se induce la fuerza electromotriz debido al
movimiento relativo de un sistema con respecto al otro.
El generador eléctrico es una máquina que siempre esta girando al mismo tiempo
que el sistema turbina-compresor, puesto que el generador eléctrico está acoplado al mismo
eje de la UTG. El generador eléctrico empieza a otorgar energía, cuando el interruptor
principal se cierra (el generador se energiza), y esto sucede cuando la velocidad del sistema
compresor-turbina tiene la velocidad de sincronismo y el sistema está listo para realizar el
empalme de energías, es decir, se tiene la misma frecuencia en el sistema que en el Sistema
Nacional1 (como un ejemplo), y la velocidad adecuada.
1
La frecuencia del Sistema Nacional es de 60 Hz.
15
CAPITULO 1
1.5.5
Unidad Turbogas
Equipo Auxiliar “Motor de Arranque”.
El equipo auxiliar de arranque puede consistir de una máquina diesel o un motor
eléctrico. Bajo operación normal, la potencia del motor de arranque de diesel o motor
eléctrico auxiliar, se transmite a través del torque del convertidor, el embrague de arranque
y los accesorios de transmisión, a la flecha de la turbina.
El equipo auxiliar de arranque tiene por función, hacer girar la flecha de la turbina
de gas desde el estado de reposo hasta la velocidad mínima de la turbina. Adicionalmente la
unidad cuenta con un dispositivo llamado virador hidráulico, el cual hace girar
periódicamente el rotor de la unidad ciertos grados durante el período de enfriamiento que
sigue a un paro, para evitar distorsiones en la flecha.
Una vez iniciado el arranque de la turbina y el encendido del combustible en la
cámara de combustión, se esperará hasta que la turbina acelere sobre la velocidad de
empuje del motor auxiliar de arranque; en ese instante el embrague de arranque se sobregira
y se pone fuera de servicio (desembraga).
1.5.6
Equipo del Sistema de Combustible.
Un sistema dual consiste de dos sistemas de combustible independientes, gas o
diesel. Este sistema está diseñado de modo que se pueda hacer automáticamente una
transferencia de un sistema a otro. La solicitud de transferencia de combustible la efectúa
el operador desde la estación de operación.
Los principales componentes del sistema de combustible diesel son: válvula de corte
de combustible, bomba de combustible y válvula de bypass.
Válvula de corte de combustible (combustible diesel. Esta válvula tiene asignada la
labor de detener el suministro de combustible, es decir, está totalmente abierta o totalmente
cerrada. Se opera por el circuito de disparo.
Bomba de combustible (combustible diesel). La bomba de combustible es
accionada por un engrane accesorio, de tipo de desplazamiento positivo de engranes. Una
válvula de alivio protege a la bomba de combustible de una sobrepresión.
Válvula reguladora o bypass (combustible diesel). Se encarga de regular la
cantidad de combustible que es retornada al sistema de combustible, controlando así el flujo
neto de combustible que va a la cámara de combustión.
En el caso del combustible gas, se cuenta con una válvula de corte, una válvula
reguladora de la presión de suministro de gas, y una válvula reguladora de combustible gas
a la cámara de combustión.
16
CAPITULO 1
1.6
Unidad Turbogas
Ecuaciones principales que rigen el comportamiento de la UTG modelo GE –
5001.
Dentro de las ecuaciones que dan el comportamiento a la UTG, se tienen diversas
variables y condiciones iniciales para cada bloque que conforma el diagrama esquemático
de la TG, tal como se muestra en la figura 1.6.
Válvula de
combustible gas
Xcgt, Piqg
Combustible: Gct
Gas: Gcgt
Aire
Comprimido
Gasc, Tacct
Válvula de
combustible diesel
Diesel: Gqclt
Cámara de
Combustión
Ggicct, Pcct, Tgcct,
Gases
Calientes
Ggit
Xqclt, Piql,
Gases de escape
Tgst
Turbina
ωt, Wft
Compresor
Wcomp
Generador
ωtr, WMW
Aire de sangrado
Aire atmosférico
Gasang, Tsang
Gaic, Patm
Figura 1.6 Sistema compresor-cámara de combustión-turbina de gas y sus variables.
A continuación en la tabla 1.1 se enlistan las variables principales de la TG:
Variable
ωt
Tabla 1.1 Variables Principales de la TG
Descripción
Velocidad angular de la turbina.
ωtr
Velocidad angular del generador.
Gaic
Flujo de aire que entra al compresor.
Gasang
Flujo que sale de las válvulas de sangrado.
Gasc
Flujo de aire que sale del compresor.
Gcgt
Flujo de combustible gas a la cámara de combustión.
Gct
Flujo total de combustible a la cámara de combustión.
Ggicct
Flujo de gases que entran a la cámara de combustión.
Ggit
Flujo de gases que salen de la cámara de combustión.
17
CAPITULO 1
Unidad Turbogas
Gqclt
Flujo de combustible diesel a la cámara de combustión.
Patm
Presión atmosférica.
Pcct
Presión en la cámara de combustión.
Piqg
Presión del combustible gas.
Piql
Presión del combustible diesel.
Tacct
Temperatura de entrada a la cámara de combustión.
Tgcct
Temperatura en la cámara de combustión.
Tgst
Temperatura de gases que salen de la turbina.
Tsang
Temperatura del flujo de aire de sangrado.
Wcomp
Energía del compresor.
WMW
Energía eléctrica producida por el generador.
Wft
Fricción en la turbina de gas.
Xcgt
Apertura de la válvula de control de combustible gas.
Xqclt
Apertura de la válvula de control de combustible diesel.
Sección del Compresor. La operación de esta unidad depende de la presión de la
cámara de combustión (considerando gas ideal), de la velocidad con que gira el sistema
compresor-turbina, de la temperatura en la cámara de combustión, además de la apertura de
las válvulas de corte de combustible (gas), válvula de sangrado y apertura de los álabes
guía, dando como variables de salida la energía que transfiere el compresor al fluido y el
flujo de aire de salida del mismo [14].
Para el caso de la Cámara de Combustión, sus variables de entrada son la presión de
entrada del combustible (gas), la energía que transfiere la compresión del fluido, la
velocidad angular del sistema compresor-turbina y la apertura de la válvula de control de
combustible (gas), por otro lado, las variables calculadas en la cámara de combustión son:
la temperatura en la cámara de combustión, la energía en la cámara de combustión, la
presión y densidad de los gases, además del flujo de los gases que salen de la cámara de
combustión.
En la Turbina se tienen como variables de entrada todas las variables de salida de la
cámara de combustión antes mencionadas, dando como variables de salida la temperatura
de gases de escape de la turbina, la energía de salida de la turbina y la velocidad angular del
sistema compresor-turbina. La tabla 1.2 muestra la nomenclatura empleada en las
ecuaciones.
18
CAPITULO 1
Unidad Turbogas
Tabla 1.2 Nomenclatura
Constantes
Simbolo
Cp
Cf
Cv
J
K
r
R
V
γ
Sub indices
Descripción
Simbolo
Calor especifico a presión constante, kJ/(kg
°K)
Coeficiente de flujo, para gases kg/(s °K1/2) y
para líquidos kg/(s kPa1/2)
Calor especifico a volumen constante, kJ/(kg
°K)
Calor de combustión, kJ/kg
Constante
Relación de velocidad generador-turbina
Constante de gas ideal (kJ/Kg-mol °K)
Volumen, m3
Relación de calor especifico (Cp/Cv)
Variables
Simbolo
A
G
H
I
P
T
Vol
W
X
ρ
ω
Descripción
acct
aic
air
asang
asc
atm
cct
cgt
cgt
comb
comp
ct
ft
g
gas
gen
gicct
Apertura de alabes guía
Flujo masico, kg/s
git
gst
Entalpia, kJ/kg
Momento de inercia, kg-m2
Presion, kPa
Temperatura absoluta, °K
Generator terminal voltage, volts
Potencia kWatts
Final control element opening
Dencidad, kg/m3
Velocidad angular, Hz
igv
iqg
iql
liq
mt
MW
qclt
sang
t
0
1,2,3,4,5
Descripción
Temperatura de entrada a la
cámara de combustion
Aire que entra al compresor
Aire
Sangrado total
Aire que sale compresor
Atmosférica
Cámara de combustión
Combustible gas
Combustible gas total
Combustible
Compresor
Combustible total
Fricción
Gases de combustión
Gas combustible
Generador
Gases que entran a la
cámara de combustión
Gases que entran a la turbina
Gases de escape de la
turbina
Entrada alabes guía
Entrada combustible gas
Entrada combustible diesel
Combustible diesel
Motor de arranque
Potencia eléctrica
Combustible diesel total
Sangrado
Turbina
0 (cero) °K,
Numero de constante
Presión en la cámara de combustión:
Teniendo la consideración de un comportamiento de gas ideal en la cámara de
combustión y de acuerdo a la ley de los gases ideales se tiene lo siguiente:
19
CAPITULO 1
Unidad Turbogas
Pcct = R g ∗ Tgcct ∗ ρ gcct
(1.1)
Flujo de aire que entra al compresor:
Ajustando el comportamiento gráfico del flujo a una ecuación de una parábola y
afectándole por la apertura de los alabes guía y la velocidad angular del eje de rotor, se
tiene la siguiente expresión:
(1.2)
Gaic = At ∗ ω t K1 ∗ − K 2 (Pcct − Patm ) − K 3
[
]
Flujo de combustible a la turbina de gas:
Se tienen dos formas de suministro del combustible: combustible líquido y
combustible gas. En el caso del combustible gas, el flujo de gas en el proceso de generación
que pasa a través de una válvula con características lineales, se comporta según la siguiente
relación:
2
(1.3)
Piqg
− Pcct2
Gcgt = X cgt ∗ Cf cgt
Tcomb
El flujo de gas proviene de la línea de PEMEX y mantiene una presión constante, no
así, para el combustible líquido, donde se tiene un depósito del cual una bomba suministra
el combustible hacia los combustores. El flujo de combustible líquido que pasa a través de
los quemadores, se comporta de acuerdo a la siguiente relación, deducida mediante el
balance de materia y energía, según lo establece la ecuación de Bernoulli.
(1.4)
Gqclt = Cf qclt Piql − Pcct
Finalmente, el flujo total de combustible a la cámara de combustión está
representado por la siguiente expresión:
(1.5)
Gct = Gcgt + Gqclt
Flujo que sale de las válvulas de sangrado:
Existe un flujo de sangrado de aire en la 4ª y la 10ª etapa del compresor, donde
juntas descargan el flujo de aire a la atmósfera durante, el arranque, lo cual evita
inestabilidad de flujo en el proceso de arranque del sistema compresor – turbina. Tomando
“Tsang” como la temperatura promedio entre la temperatura de entrada y salida del
compresor, se tiene lo siguiente:
(1.6)
T + Tacct
Tsang = atm
2
El flujo de sangrado total (4ª y 10ª etapas) se puede aplicar la expresión de flujo de
gases a través de una restricción, y considerando a la válvula con característica de flujo
lineal, tenemos lo siguiente:
2
2
(1.7)
Pcct − Patm
G asang = X sang * Cf sang
T sang
20
CAPITULO 1
Unidad Turbogas
Flujo de aire que sale del compresor:
El flujo de aire que sale del compresor y que entra a la cámara de combustión, se
determina por la resta entre el flujo de aire que entra al compresor menos el flujo que sale
por el sangrado:
(1.8)
Gasc = Gaic − Gasang
Flujo de gases que entran a la cámara de combustión:
El flujo de gases de combustión es la suma del flujo de aire que sale del compresor
más el flujo de combustible que entra:
(1.9)
G gicct = Gasc + Gct
Temperatura de entrada en la cámara de combustión:
Considerando una compresión isentrópica del aire en el compresor, la temperatura
del aire comprimido se obtiene mediante la siguiente relación:
Yair
(1.10)
Pcct
Cp air
Tacct =
∗ Tatm
donde Yair =
Patm
Cv air
Temperatura de gases de escape que salen de la turbina:
Para los gases de escape se considera que presentan un comportamiento de gas
ideal, por lo que un proceso de expansión isentrópica a través de la turbina de gas se
obtiene bajo la siguiente relación:
Yg
(1.11)
γ g −1
Patm
Tgst = Tgcct ∗
donde
Yg =
Pcct
γg
Temperatura en la cámara de combustión:
A través de un balance de energía dinámico en la cámara de combustión, se obtiene
la expresión dada por una diferencial de la temperatura dentro de esta cámara respecto al
tiempo; quedando en función de cambios presentados en los flujos de entrada (energía que
entra) y los de salida (energía que sale), la energía generada por la combustión de ambos
combustibles, así como lo que se acumula en los flujos que residen dentro de esa cámara.
dTgcct Gasc * Cpair (Tatm − T0 )
Gcgt * J gas
Gqclt * J liq
=
+
+
dt
Cpg * ρ gcct * Vcct
Cpg * ρ gcct * Vcct Cpg * ρ gcct * Vcct
G (T − T0 ) (Tgcct − T0 )(Ggicct − Ggit )
− git gcct
−
ρ gcct * Vcct
ρ gcct * Vcct
21
(1.12)
CAPITULO 1
Unidad Turbogas
Velocidad de giro del generador:
Debido a que el generador gira a diferente velocidad que la turbina de gas, la
relación entre las velocidades angulares está dada por las dimensiones de los engranes en
contacto en la transmisión que se mantiene constante
(1.13)
ω gen = ω t ∗ r
Fricción en turbina de gas:
El trabajo de fricción entre las diversas partes en movimiento y en las fijas del
sistema compresor – turbina – generador, se propone proporcional [14]a la velocidad de
giro:
(1.14)
W ft = K comb ∗ ω t
Velocidad angular del sistema compresor_turbina:
La rapidez con la que se acumula la energía cinética rotacional en el eje del sistema
compresor – turbina – generador depende del balance de energía [15].
(1.1)
dω t I tg1
=
G git ∗ (H cct − H gst ) + Wmt − WMW − W ft − Wcomp
ωt
dt
[
1.6.1
]
Datos de operación de la TG-5001
El modelo de la turbina de gas en la que nos basamos para realizar este trabajo de
tesis es la TG modelo GE-5001, la cual es una máquina de ciclo simple de un sólo eje,
con las siguientes características [16]:
Datos del Generador Eléctrico
Marca:
Capacidad:
Voltaje:
Factor de potencia:
Velocidad:
Frecuencia:
Núm. fases:
Tipo de aislamiento:
Tipo de excitador:
Voltaje/excitación:
Corriente/excitación:
Hitachi-GE
30,313 KVA
13800 V
0.8
3600 RPM
60 Hz
3 fases
Clase F
Estático
285 V
276 A
Datos de la Turbina
Marca:
Modelo:
Sistema de control:
Altitud:
Etapas de la turbina:
Hitachi-GE
PG5341
Speedtronic MARK-II
20 metros sobre el nivel del mar
2
22
CAPITULO 1
Velocidad:
Capacidad carga pico:
Unidad Turbogas
Temperatura de entrada:
Presión de entrada:
Temperatura de escape:
Presión de escape:
Sistema de combustible:
Sistema de arranque:
Accesorios:
5,100 RPM
25,980 KW (Gas Natural)
25,440 KW (Diesel)
15°C
760 mmHg
486°C
760 mmHg
DUAL (Gas Natural/Diesel)
Máquina Diesel de 500 HP
TYPE-A500
Datos del Compresor
Tipo:
Etapas del compresor:
Flujo Axial
17
1.7
Conclusiones
Las turbinas de gas a diferencia de otros impulsores primarios, se caracterizan por
ocupar poco espacio en su instalación, arranques rápidos, poca asistencia técnica durante su
operación y costos de instalación bajos. Debido a esto, en las ultimas décadas las UTG han
desempeñado un papel importante en la generación de energía eléctrica.
El uso de un modelo matemático es muy importante, ya que nos permite realizar
pruebas y simulaciones a nivel laboratorio, así como adaptar diferentes estrategias de
control para controlar un proceso, y seleccionar la mas adecuada para su posterior
aplicación al proceso real.
23
CAPITULO 2
Control Convencional de la Unidad Turbogas
Control Convencional de la Unidad
Turbogas
2.1
Introducción.
Este capítulo se presenta un panorama general de la evolución de los sistemas de
control empleados para la operación de las TG, así como también se mencionan los
requerimientos fundamentales de control para imponer en la turbina aspectos de máxima
seguridad, disponibilidad y eficiencia. Además, se muestra el esquema de control actual
con el cual se opera la TG, el cual esta compuesto por un circuito dual de control de
velocidad y carga, se describe el tipo y configuración de cada controlador que compone
este esquema y se analiza el comportamiento del mismo, remarcando las principales
desventajas que posee.
24
CAPITULO 2
2.2
Control Convencional de la Unidad Turbogas
Evolución de los sistemas de control para unidades turbogas
La TG fue introducida como fuente de energía primaria a finales de los 40’s. Los
primeros sistemas de control estuvieron basados en sistemas hidro-mecánicos, los cuales
mediante secuencias manuales permitían un control práctico en las turbinas de vapor.
La secuencia automática de arranque fue la base para la introducción del primer
control electrónico de la TG a finales de los 60´s. Los rápidos avances en la tecnología de
sistemas electrónicos propiciaron la modernización de los sistemas de control de las TG´s,
apareciendo el control electrónico a inicios de los 70’s. Para mediados de los 80´s, se
introdujeron técnicas de automatización de TG´s mediante implementación digital y
actualmente se cuenta con sistemas de control digital, los cuales integran funciones de
control de arranque, velocidad, generación y temperatura que cumplen con los
requerimientos de alta exactitud, confiabilidad, flexibilidad y respuesta rápida
indispensables ya que las TG´s operan a altas temperaturas y velocidades [17].
2.3
Requerimientos de control de una unidad turbogas
Con el fin de obtener seguridad, disponibilidad y eficiencia en la turbina de gas, se
requiere de un sistema de control efectivo para que realizar las siguientes acciones [18]:
1)
mantener la estabilidad de la unidad después de una perturbación y mantener la
precisión de la respuesta en operación normal,
2)
que durante el arranque, obtener la respuesta más precisa en el seguimiento de las
curvas de aceleración, lo cual minimizará el uso de combustible antes de la
sincronización y los períodos de alta vibración,
3)
en generación, mantener a la unidad trabajando a altas temperaturas y presiones
muy cercanas a los límites de disparo por ser el punto de máxima eficiencia de la
unidad, pero sin excederlos para conservar la disponibilidad de la unidad.
4)
con el fin de incrementar la confiabilidad en los arranques, la secuencia de arranque,
incremento de velocidad, sincronización y toma de carga se efectué
automáticamente, ante una orden del operador de la unidad.
De acuerdo a lo anterior, el sistema de control debe llevar a cabo seis funciones
fundamentales:
1)
2)
3)
4)
5)
6)
Secuencia de arranque y paro.
Control de velocidad.
Control de potencia.
Control de temperatura.
Protección del equipo turbogas.
Interacción entre operador-sistema.
25
CAPITULO 2
Control Convencional de la Unidad Turbogas
Cada una de estas funciones tiene requerimientos específicos que deben ser tratados
de manera particular. A continuación mencionaremos algunos de estos aspectos.
2.3.1
Secuencia
Módulo lógico del sistema de control que se encarga de realizar un conjunto de
operaciones en forma ordenada, segura y sucesiva, de tal manera que el arranque y paro de
la turbina de gas se efectúen adecuadamente de acuerdo a una secuencia de eventos preestablecida (figura 2.1).
C A R G A
(MW)
La secuencia proporciona las señales discretas o de “encendido-apagado” a diversos
equipos que intervienen en el conjunto de operaciones secuenciales, tales como
arrancadores de motores, válvulas solenoides, luces indicadoras y relé de ignición. Además
de las señales requeridas para operación normal y segura, el sistema de secuenciamiento
también debe proporcionar aquellas señales necesarias para poner fuera de servicio a la
unidad en caso de condiciones anormales de operación, incluyendo fallas del equipo o del
sistema de control.
CARGA PICO
25
20
CARGA BASE
15
10
5
5100
VELOCIDAD DE SINCRONISMO
4945 - 5100 R. P. M.
4600
CARGA MINIMA
INTERRUPTOR
PRINCIPAL CERRADO
CIERRE DE VALVULAS
DE SANGRADO
APERTURA DE
ALABES GUÍA
V E L O C I D A D
(RPM)
4200
3800
3400
3000
2600
2200
MOTOR DE ARRANQUE FUERA (2140 R. P. M.)
1800
1400
PUNTO DE IGNICION (1020 R. P. M.)
1000
600
200
0
MOTOR DE ARRANQUE ENCENDIDO
VERIFICACIÓN DE PERMISIVOS DE ARRANQUE
SELECCIÓN Y SUMINISTRO DE COMBUSTIBLE
BOMBA DE ACEITE ENCENDIDA
Figura 2.1 Secuencia de arranque
26
T I E M P O
CAPITULO 2
Control Convencional de la Unidad Turbogas
Requerimientos de Arranque
Esta función tiene como objetivo conducir y supervisar al equipo Turbogas durante
el proceso de arranque hasta alcanzar la velocidad de sincronizmo donde la frecuencia y el
voltaje del generador deben igualarse con los del sistema eléctrico interconectado.
Los eventos mínimos que deberán realizarse, para desarrollar correctamente la
secuencia de arranque son:
•
Permisivos de arranque. Los permisivos de arranque corresponden al
restablecimiento de auxiliares (agua de enfriamiento, banco de baterías, sistema
detección de fuego, sistema de alimentación de corriente directa, etc.), de disparos y
a la indicación de los ignitores apagados, necesarios para generar la solicitud de
arranque e inicio de secuencia.
•
Listo para arrancar. Con base en la solicitud de arranque, se abren las válvulas de
sangrado en el compresor y se cierran los álabes guía (esto para aportar mayor
fuerza sobre los álabes).
•
Arrancar. Al activar el estado operativo de arranque de la turbina a través de la
estación de operación IHM (Interfaz Hombre Maquina), se indica que el arranque es
normal y exitoso.
•
Secuencia en progreso. Cuando la secuencia está en progreso, se activa la bomba de
suministro de combustible; al mismo tiempo se selecciona cual de los combustibles
(gas o diesel) será utilizado durante el arranque.
•
Comienza el dispositivo auxiliar de arranque. Automáticamente se activa el
dispositivo mecánico auxiliar, el cual puede ser un motor eléctrico o una máquina
diesel, que es utilizado como impulsor inicial de la velocidad de la turbina (para el
caso aquí expuesto se trata de un motor).
•
Velocidad mínima en la turbina. Al 20 % de la velocidad de la turbina (1020 r.p.m.),
se activa el estado operativo que indica la velocidad mínima de operación de la
turbina.
•
Detección de flama. A la velocidad mínima se encienden los ignitores para iniciar
el proceso de ignición en la cámara de combustión. Al detectar flama, la la válvula
de combustible se mantiene en una apertura mínima (0.2%) para un período de
calentamiento de 60 seg.
•
Rampa de aceleración. Al término del periodo de calentamiento se incrementa el
flujo de combustible siguiendo la trayectoria de la rampa establecida por el operador
de la turbina.
27
CAPITULO 2
Control Convencional de la Unidad Turbogas
•
Velocidad de aceleración. Cuando la velocidad de la turbina llega al 40% (2040
r.p.m.), se denota como régimen de aceleración. A esta velocidad se desembraga el
dispositivo de arranque auxiliar.
•
Secuencia completa. Cuando la velocidad de la turbina alcanza el 95% (4845 r.p.m.)
se indica que está en velocidad de sincronismo, entonces se abren los álabes guía de
entrada de aire al compresor y se cierran las válvulas de sangrado en el mismo. El
rango de velocidad de 4845 r.pm. y 5100 r.p.m. se denomina “velocidad de
sincronismo”.
Sincronización.
•
Cierre del interruptor de campo del generador. A la velocidad de sincronismo (95%)
se cierra el interruptor de campo del generador con la finalidad de energizar al
generador.
•
Cierre del interruptor principal del generador (conecta al generador con el sistema
eléctrico nacional). el cierre del interruptor principal puede ser en forma manual o
automática, este último a través del sincronizador. Si la sincronización es realizada
automáticamente, el equipo de sincronización genera los comandos de incrementar
o disminuir la velocidad en la turbina hasta igualar la frecuencia del generador con
los del sistema eléctrico en línea, en tanto, el voltaje en terminales requerido para la
sincronización es controlado por el regulador automático de voltaje. Cuando la
frecuencia y el voltaje del generador están en fase con los del sistema eléctrico en
línea, se cierra el interruptor principal del generador.
•
Toma de carga. Al cerrarse el interruptor principal del generador, finaliza la
secuencia de arranque.
Paro.
En general, el paro de la turbina de gas puede ser normal o de emergencia:
1.
Paro normal. Consiste en un procedimiento paso a paso, ordenado y seguro, para
poner fuera de servicio a la unidad. Puede ser realizado en forma manual o
automática. Con el paro normal, la unidad queda habilitada para que se pueda
efectuar un nuevo arranque (arranque en caliente).
2.
Paro de emergencia. Puede ser activado manualmente, pero también debe ocurrir
como resultado de la operación automática de los dispositivos de protección
correspondientes. En este caso, el sistema debe generar las señales requeridas
para cerrar la válvula de alimentación de combustible y cortar el suministro del
mismo a la turbina.
28
CAPITULO 2
Control Convencional de la Unidad Turbogas
Los sistemas de control de la turbina y del generador eléctrico deben mantener una
relación conveniente. En caso de paro de la turbina, se debe contar con medios automáticos
para aislar al generador del sistema eléctrico de potencia al que se encuentra conectado, con
el fin de prevenir el flujo inverso de potencia (motorización del generador).
Protección
El sistema de control debe incorporar las verificaciones de seguridad necesarias y
suficientes a fin de garantizar la integridad del equipo y del personal que labora en el área
empleando equipos redundantes para reducir al mínimo la posibilidad de accidentes.
La protección comprende las funciones que previenen la operación anormal del
equipo. Su objetivo principal es prevenir daños al personal. Los requerimientos secundarios
se refieren a la prevención de daños a los equipos principales y auxiliares, aumentando al
máximo el nivel de disponibilidad de la unidad y reduciendo considerablemente los costos
de mantenimiento.
El sistema de protección es un respaldo independiente para el sistema de control que
garantiza la operación segura de la turbina. Las funciones de protección más comunes son:
sobre-velocidad, sobre temperatura, pérdida de flama, alta vibración, baja presión del aceite
lubricante, alta temperatura del aceite lubricante, fuego y falla del equipo de control.
2.3.2
Control de Velocidad
El control de velocidad se realiza mediante la regulación del flujo de combustible
alimentado a la cámara de combustión de la turbina, lo cual proporciona las siguientes
funciones básicas:
•
Control de ignición y aceleración: El control de combustible establece el flujo de
combustible para la ignición. Después de verificar que se ha establecido la flama, el
control incrementa el flujo de combustible que a su vez acelera la turbina hasta un
valor predeterminado, punto donde el control de velocidad entra en operación.
Durante este periodo de aceleración, el control de combustible debe prevenir el flujo
excesivo del mismo para evitar daños a la turbina.
•
Control de Velocidad en estado estable: Una vez que la turbina alcanza su
velocidad nominal de operación, el control de combustible debe regular este valor
de estado estable ya que, para el caso de una unidad generadora de energía eléctrica,
es la velocidad quien determina la frecuencia nominal del voltaje de c.a.
•
Control durante condiciones transitorias: Las turbinas experimentan transitorios
(rechazo de carga, salida de operación de grandes motores, cambios en la
frecuencia, etc.). El controlador de velocidad debe incrementar o disminuir
rápidamente el flujo de combustible de acuerdo a una cierta razón de cambio,
después de cualquier movimiento de carga que se presente.
29
CAPITULO 2
Control Convencional de la Unidad Turbogas
Una turbina de gas consiste de un sistema que desarrolla un par (compresor, cámara
de combustión y turbina), y de una carga impulsada, con un par que se opone al par
desarrollado. La cantidad de par desarrollado depende directamente del flujo de
combustible suministrado a la turbina. Durante condiciones de estado estable, el par de la
carga es constante y el par desarrollado debe ser suficiente para mover el compresor, vencer
la fricción interna y desarrollar un par igual al de la carga impulsada. Durante condiciones
transitorias, cuando el par de carga cambia, se produce un desbalance entre éste y el par
desarrollado lo cual ocasiona un cambio en la velocidad. Por lo tanto, la tarea del
controlador de velocidad es muy importante, debe mantener condiciones estables de
operación y, después de un cambio de carga debe regresar la velocidad al valor de estado
estable con un mínimo de oscilaciones (sobre impulsos) y en el menor tiempo posible.
El controlador de velocidad compara el valor de referencia (punto de ajuste) con el
valor de velocidad medido y actúa sobre el sistema de combustible. Para el caso de turbinas
del tipo de un sólo eje, el compresor, la turbina y la carga están montados en una flecha
común. Por lo tanto, únicamente está involucrado un parámetro de velocidad.
El combustible alimentado a la turbina debe ser controlado durante todo el régimen
de operación, desde la ignición inicial hasta su condición máxima de operación, así como
también durante las condiciones de aceleración y desaceleración.
2.3.3
Control de Potencia
El control de potencia comienza una vez que el interruptor del generador fue
cerrado y comienza la generación de una potencia mínima (aproximadamente para ésta
turbina Modelo GE-5001 es de 2 MW). Esto se hace para que la energía generada comience
con una rampa ascendente, de lo contrario la generación puede cambiar con un pico grande
o cambio brusco en el inicio de la potencia, lo que puede provocar problemas en la línea de
generación.
Cualquier incremento de carga requiere de un incremento en el flujo de
combustible. Sin embargo, la correspondencia entre estos eventos no puede continuar más
allá de los límites de diseño de la turbina, es decir, de la potencia y temperatura máximas de
operación en las que influyen fundamentalmente las condiciones del medio ambiente.
Cuando la demanda de potencia aumenta, el controlador de velocidad incrementa el
flujo de combustible. A un cierto nivel de combustible, la turbina alcanza su potencia de
diseño máxima. Para una turbina de eje simple, este nivel puede estar determinado por el
valor máximo del punto de ajuste, por la cantidad máxima de combustible permitido o por
el límite de temperatura de operación. En estas situaciones, la turbina debe comenzar a
operar a un nivel de potencia fijo. Cualquier incremento en la demanda de potencia más allá
de este valor máximo producirá una disminución en la velocidad o la activación de alguna
protección que pueda poner fuera de operación a la unidad.
Una turbina acoplada a un generador eléctrico que opera aisladamente debe
mantener una frecuencia constante. Por lo tanto, la turbina debe tener una capacidad
suficiente para proveer toda la potencia requerida sin rebasar los límites de operación
30
CAPITULO 2
Control Convencional de la Unidad Turbogas
permitidos (por ejemplo limite de temperatura de gases de escape impuesto por el
fabricante). Cuando por el contrario, el generador eléctrico se encuentra conectado a un
gran sistema eléctrico de potencia, frecuentemente suministra potencia base y, por lo tanto,
opera a su nivel máximo de potencia. En estas condiciones, el nivel de precisión y exactitud
del controlador de velocidad y del controlador de temperatura juegan un papel
trascendental.
La potencia mecánica de salida de una turbina de gas que opera a velocidad o
temperatura constante varía en función de la temperatura ambiente. En este caso, cuando la
temperatura ambiente baja, la masa de aire por pie cúbico se incrementa y, por lo tanto, existe
también un incremento en el flujo de aire a través del compresor. Debido a que la potencia de
la turbina es proporcional al flujo másico de los gases, entonces un cambio en la temperatura
ambiente provoca un cambio correspondiente en la potencia de salida de la turbina y, por lo
tanto, en la potencia eléctrica de un generador que opera en paralelo con un sistema eléctrico
de potencia
2.3.4
Control de Temperatura
El control de temperatura es sumamente importante para la vida útil de la UTG,
debido a que las altas temperaturas indeseadas provocan daños irreparables en los
componentes y elementos que constituyen a la UTG. La medición de la temperatura de la
Turbogas se realiza por medio de un grupo de termopares situados estratégicamente en la
UTG, estos termopares generan señales en milivolts que son enviadas al sistema de control,
para su comparación e interpretación del ajuste sobre la válvula de combustible, si así fuese
requerido.
Si la temperatura límite de la turbina de gas es excedida, sus partes se desgastan más
rápido y pueden llegar a deteriorarse completamente, causando daños severos a la misma e
inclusive al equipo y personal cercanos a ella.
Un incremento en la demanda de potencia requiere un flujo de combustible mayor,
lo cual produce un incremento en la temperatura de operación de la turbina. Esta
temperatura debe ser limitada al valor máximo permitido impuesto por el fabricante.
2.4
Esquema actual de control (Típico)
El control automático de la UTG abarca todos los requerimientos de la operación,
desde el arranque inicial hasta el paro final.
Típicamente la estrategia general de control utilizada para la operación de la UTG
consiste en la regulación de flujo de combustible. El núcleo del esquema de control está
formado básicamente por un circuito dual de control de velocidad y carga para la
regulación de flujo de combustible.
El control de velocidad, potencia y temperatura se lleva a cabo mediante el circuito
de control que muestra la figura 2.2. Este esquema de control principalmente está
compuesto por un control de velocidad, implementado con un algoritmo PI digital, el cual
31
CAPITULO 2
Control Convencional de la Unidad Turbogas
se encuentra en una configuración retroalimentada como lo muestra la figura 2.3, así como
un control de potencia basado también en un algoritmo PI digital en un esquema
retroalimentado. Además de estos 2 controladores principales también existe un control
supervisor de temperatura, conformado por un PI digital retroalimentado.
+
Ref.
Vel.
PI Vel.
-
+
+
+
Ref.
MW
PI MW
-
<
Vel.
UTG
MW
TGE
+
Ref.
TGE
sc
-
PI TGE
Figura 2.2 Esquema Actual de Control de velocidad, potencia y temperatura.
Donde:
Ref. Vel.
+
-
Ref. Vel.
Vel.
Ref. MW
MW
Ref. TGE
TGE
sc
<
error
Curva de referencia de la velocidad.
Velocidad medida de la turbina de gas
Curva de referencia de la potencia.
Potencia generada por la TG.
Curva de referencia de la temperatura de gases de escape
Temperatura de gases de escape de la TG.
Señal de control
Selector de menor señal
PI
Velocida
d
sc
Velocidad
UTG
Medición
Figura. 2.3 Diagrama a Bloques del Lazo de Control de Velocidad
Básicamente la operación del esquema de control presentado en la figura 2.2 se
puede describir en dos etapas principales: etapa de arranque y etapa de generación, en cada
una de las cuales se presentan diferentes pertubarciones y eventos.
Durante la etapa de arranque, el esquema de control que se encuentra en operación
es el control de velocidad, quien regula el flujo de combustible hacia a la cámara de
32
CAPITULO 2
Control Convencional de la Unidad Turbogas
combustión a través de la válvula de combustible, de tal manera que se pueda lograr el
mejor seguimiento de la curva de referencia de velocidad.
La señal de control es calculada por un algoritmo PI convencional, a partir del error
de seguimiento de velocidad, el cual es la diferencia entre la curva de referencia y la
velocidad angular de la UTG.
Durante la etapa de arranque el control de velocidad debe contrarrestar
perturbaciones del proceso que son significativas, por ejemplo el sobre flujo de aire en la
cámara de combustión provocado por el cierre de las válvulas de sangrado del compresor.
Cuando se lograr alcanzar la velocidad de sincronismo, el interruptor principal del
generador es cerrado para enlazar la unidad turbogas a la red eléctrica, comenzando así la
etapa de generación. En este instante, el control de potencia es habilitado para llevar a la
unidad turbogas a generar la potencia mínima con la finalidad de evitar una motorización
del generador, al mismo tiempo el control de velocidad es colocado en un estado latente
manteniendo el último valor antes de la sincronización como una contribución a la señal de
control. Después de esto, el control PI de potencia se encarga de generar la señal de control
necesaria para suministrar la potencia solicitada por el operador. La señal de control a la
válvula de combustible es calculada por un algoritmo de control PI a partir del error de
potencia generada.
Durante las dos etapas descritas anteriormente, también se encuentra actuando un
controlador de temperatura como lo muestra la figura 2.2. Este se encarga de proteger a la
UTG cuando la demanda de combustible solicitada por el control de velocidad y/o de
potencia se incrementa provocando que se incremente la temperatura de los gases de
escape por arriba de los límites establecidos por el fabricante. Como consecuencia el PI de
temperatura toma el control de la UTG hasta regular la temperatura, después devuelve el
control al PI que se encontraba en operación de acuerdo a la etapa de operación vigente.
El control de temperatura es crítico para la eficiencia, vida útil y potencia generada.
Mientras la turbina se opere lo más cercano posible a su temperatura límite, más alta será su
eficiencia y su potencia de salida. Por otra parte, si la temperatura límite de la turbina de
gas es excedida, sus partes se desgastan más rápido y pueden llegar a deteriorarse
completamente, causando daños severos a la turbina e inclusive al equipo y personal
cercanos a la misma.
2.5
Comportamiento del control actual
En esta sección se realiza un análisis del desempeño del esquema de control actual
basándose en las respuestas de la velocidad de la turbina de gas, de la temperatura de los
gases de escape, y de la potencia generada por la turbina de gas, estas respuestas se
muestran el la figura 2.4, con la finalidad de analizar su comportamiento. Estas respuestas
fueron obtenidas con el sistema para desarrollo y validación de algoritmos de control para
turbinas de gas, desarrollado en ambiente Simulink [19] (ver anexo A). Posteriormente
en el capítulo 5 se analizará mejor el desempeño del esquema actual de control, por medio
de índices de error y pruebas de rechazo a disturbio.
33
CAPITULO 2
Control Convencional de la Unidad Turbogas
Figura 2.4 Gráfica de las respuestas de la turbina
Como se observa en la figura 2.4, de acuerdo a la secuencia de arranque el primer
componente en entrar en operación es el motor de arranque, después que finaliza el periodo
de calentamiento (aprox. a los 120 seg) se activa la rampa de aceleración, el primer control
en entrar en acción es el control de velocidad, el cual comienza a regular la velocidad de
acuerdo a la curva de referencia, debido a que la velocidad se va incrementado
gradualmente, el controlador también incrementa la demanda de combustible para lograr el
mejor seguimiento de la curva de referencia, pero este incremento de la demanda de
combustible provoca que se eleve la temperatura por encima de la referencia (véase la
figura 2.4), provocando que el PI supervisor de temperatura tome el control
(aproximadamente a los 150 seg.) hasta regular la misma, después el control de velocidad
retoma el mando (aproximadamente a los 280 seg.) hasta llevar a la TG a la velocidad de
sincronismo para ceder después el control al PI de potencia (aproximadamente a los 400
seg.) .
En la figura 2.4 se observa como el PI de potencia se encarga de llevar a la TG a
carga mínima (2 MW) y después a la demanda solicitada por el operador (20 MW). Sin
embargo, como se observa en la figura la potencia máxima generada por la TG es aprox.
10.7 MW, debido a que la temperatura de los gases de escape de la TG se incrementa,
aproximándose al límite máximo de diseño (aproximadamente a los 475 seg.), ocasionando
que el PI supervisor de temperatura tome nuevamente el control para regular la temperatura
de acuerdo a la referencia de como se observa en la figura 2.4. cuando la demanda de carga
34
CAPITULO 2
Control Convencional de la Unidad Turbogas
disminuye, provocando que también disminuya la temperatura, por lo que el PI de potencia
vuelve a retomar el control (aproximadamente a los 820 seg.) .
2.6
Problemática del control actual
Como se puede observar en las gráficas anteriores, una de las mayores desventajas
que presenta el control actual es la fuerte interacción que existe entre los controladores, ya
que estos son controladores independientes que operan sobre un mismo elemento final de
control (válvula de flujo de gas combustible). Por ejemplo, una variación en los parámetros
del controlador PI de temperatura, no sólo afectará el desempeño del control de
temperatura, sino que también afectará el desempeño del control de velocidad y potencia,
esto se puede observar en las figuras 2.5, 2.6 y 2.7. En estas graficas se muestra las
repuestas normales presentadas en la grafica 2.4 obtenidas del sistema para desarrollo y
validación de algoritmos de control para turbinas y estas se comparan con las respuestas
obtenidas con el mismo sistema al variar un solo parámetro del PI de temperatura.
En la grafica 2.5 se observa como la variación del parámetro del controlador de
temperaturas afecto la respuesta de velocidad, empeorando el seguimiento de la curva de
referencia. En la grafica 2.6 se observa como con la variación de este parámetro se logra
regular mejor la temperatura durante la etapa de arranque, pero esta regulación empeora
durante la etapa de generación, provocando la generación de una menor potencia, tal como
se muestra en la figura 2.7.
Figura 2.5 Gráfica de la velocidad de la turbina ante ajuste de los parámetros en el PI de
temperatura
35
CAPITULO 2
Control Convencional de la Unidad Turbogas
Figura 2.6 Gráfica del comportamiento de la temperatura de la turbina ante ajuste de los
parámetros en el PI de temperatura
Figura 2.7 Gráfica de la potencia de la turbina ante ajuste de los parámetros en el PI de temperatura
36
CAPITULO 2
Control Convencional de la Unidad Turbogas
Otra desventaja como se observa en la figura 2.4 es que cuando el control de
temperatura toma el mando durante la etapa de arranque de la TG, en un principio este no
alcanza a regular bien la temperatura de los gases de escape de la misma sobrepasando
ligeramente el límite establecido (aprox. de 175 a 280 seg), lo que puede provocar que las
partes de la turbina se desgasten más rápido o lleguen a deteriorarse completamente.
Durante esta etapa la regulación de temperatura se puede mejorar ajustando los parámetros
del PI de temperatura, pero esto causará otras alteraciones al sistema de control, por
ejemplo como se muestra en la figura 2.6 la regulación en la temperatura durante la etapa
de arranque mejoró, pero provocó que la regulación en la etapa de generación muestre un
desempeño más pobre como se observa en la figura 2.7, disminuyendo con ello la eficiencia
de la TG.
En cuanto al seguimiento de las curvas de referencia correspondiente a los lapsos en
que cada controlador está operando, se puede decir que es aceptable, pero susceptible de
mejorarse con la aplicación del controlador neurodifuso lo cual se verá en el capítulo 4. En
las figuras 2.8 y 2.9 se muestran los errores de seguimiento durante la etapa de arranque y
de generación.
Error de seguimiento de velocidad
Figura 2.8 Gráfica del error de la velocidad de la TG.
37
CAPITULO 2
Control Convencional de la Unidad Turbogas
Figura 2.9 Gráfica del error de la potencia de la turbina
Otras desventajas generales que presentan los controladores convencionales del tipo
PI es que son diseñados para tareas de regulación y rechazo a perturbaciones y no para
seguimiento de puntos de referencia en forma de rampa. Las UTG’s presentan un
comportamiento no lineal y variante en el tiempo, principalmente en la etapa de arranque
donde se presentan varios disturbios importantes, actualmente los controladores utilizados
en los lazos de control de la UTG son lineales, y son sintonizados para un punto de
operación específico y conservados así por tiempo indefinido, lo que puede desfavorecer su
desempeño en los puntos distantes de operación donde fueron sintonizadas sus ganancias.
2.7
Conclusiones
Actualmente el control de las turbinas de gas esta implementado con algoritmos de
control tipo PI debido a las ventajas que posee como son:
•
•
•
•
Es el algoritmo de control mas comúnmente usado en la industria, debido a
su versatilidad, elevada confiabilidad y fácil operación.
Existen muchos métodos para diseñar el controlador.
Ofrecen una gran variedad de maneras de utilizar la información de los
modelos matemáticos para hacer un buen control.
Tiene un desempeño aceptable.
Sin embargo, este algoritmo de control también posee algunas desventajas como las
detalladas en este capitulo, algunas de las cuales son:
38
CAPITULO 2
•
•
Control Convencional de la Unidad Turbogas
Son diseñados para tareas de regulación y rechazo a perturbaciones y no
para seguimientos de puntos de referencia.
Los controladores PI presentan un comportamiento lineal, mientras la
turbina de gas presenta un comportamiento no lineal e invariante en el
tiempo.
Aunadas a estas desventajas también se presentan las derivadas de la estrategia de
control utilizada para el control de la UTG, las cuales son:
•
•
La fuerte interacción que existe entre los controladores.
La temperatura de los gases de escape no es regulada correctamente, lo cual
implica mayores mantenimientos y la reducción de la vida útil de la UTG.
39
CAPITULO 3
Control Prealimentado Neurodifuso Multivariable
CONTROL PREALIMENTADO
NEURODIFUSO MULTIVARIABLE
3.1
Introducción.
En este capítulo se describe el desarrollo de un controlador prealimentado
multivariable, para actuar en conjunto con el esquema de control retroalimentado existente,
con la finalidad de reducir las desventajas del esquema convencional de control
mencionadas en el capítulo anterior. De tal modo que el controlador prealimentado aporte
la mayor parte de la señal de control y los controladores PI retroalimentados proporcionen
el complemento de la señal de control necesaria para realizar ajustes finos y rechazar
disturbios.
Se propone diseñar el control prealimentado como un sistema neurodifuso, debido a las
ventajas que esta estrategia de control presenta, y las cuales se describen en este capítulo.
40
CAPITULO 3
3.2
Control Prealimentado Neurodifuso Multivariable
Control prealimentado
El combinar el control retroalimentado con el control prealimentado puede mejorar
significativamente el desempeño sobre un control retroalimentado simple, siempre que
haya un disturbio que pueda ser medido antes de que este afecte la salida del proceso. En
una situación ideal el control prealimentado puede eliminar enteramente los efectos del
disturbio medido en la salida del proceso. Incluso cuando hay errores en el modelado, el
control prealimentado frecuentemente reduce los efectos del disturbio medido en la sálida
mejor que lo alcanzado con sólo un controlador retroalimentado.
La estrategia de control prealimentada puede ser clasificada como de múltiples
entradas y una sola salida (MISO) si se requiere más de una medición de proceso, pero
solamente existe un elemento final de control, como ocurre en la turbina de gas, donde nos
interesa controlar la velocidad, potencia y temperatura (entradas) y sólo tenemos un
elemento final de control (válvula de control de combustible) para lograr este objetivo.
Existen varias técnicas o configuraciones para realizar una estrategia de control
prealimentado, la estrategia de control empleada para el desarrollo de este trabajo de tesis
se deriva de la configuración del control lineal de dos grados de libertad mostrado en la
figura 3.1 [9].
Yd(s)
Control
Prealimentado
Gff(s)
U(s)
Uff(s)
+
+
Ufb(s)
UTG
Gp(s)
Y(s)
Control Retroalimentado Gfb(s)
E(s)
-
+
Figura 3.1 Configuración del control de dos grados de libertad.
Donde:
Yd(s)
Y(s)
Uff(s)
Ufb(s)
U(s)
Señal de referencia
Salida de la planta
Señal de control prealimentado
Señal de control retrolaimentado
Señal de control total
Analizando las funciones de transferencia del diagrama de bloques de la figura 3.1
tenemos las siguientes ecuaciones:
Y ( s ) = Gp ( s )U ( s )
U ( s ) = Uff ( s ) + Ufb ( s )
(3.1)
(3.2)
Uff ( s ) = Yd ( s )Gff ( s )
Ufb ( s ) = [Yd ( s ) − Y ( s )]Gfb ( s )
(3.3)
(3.4)
41
CAPITULO 3
Control Prealimentado Neurodifuso Multivariable
Sustituyendo las ecuaciones 3.3 y 3.3 en la ecuación 3.2, tenemos:
U ( s ) = Yd ( s )Gff ( s) + [Yd ( s) − Y ( s )]Gfb( s )
(3.5)
Sustituyendo la ecuación 3.5 en la ecuación 3.1 y reduciendo, tenemos:
Y ( s ) = Gp ( s )[Yd ( s )Gff ( s ) + [Yd ( s ) − Y ( s )]Gfb( s )]
Y ( s ) = Gp ( s )Yd ( s )Gff ( s ) + Gp ( s )[Yd ( s) − Y ( s )]Gfb( s )
Y ( s ) = Yd ( s )Gff ( s )Gp ( s ) + Yd ( s )Gfb( s )Gp ( s ) − Y ( s )Gfb( s )Gp ( s )
Y ( s ) = Yd ( s )[Gff ( s )Gp ( s ) + Gfb( s )Gp ( s )] − Y ( s )Gfb( s )Gp ( s )
Y ( s ) + Y ( s )Gfb( s )Gp ( s ) = Yd ( s )[Gff ( s )Gp ( s ) + Gfb( s )Gp ( s )]
Y ( s ) = Yd ( s )[Gff ( s )Gp ( s ) + Gfb( s )Gp ( s )][1 + Gfb( s )Gp ( s )]
−1
Si hacemos
[
G ff ( s ) = G p ( s)
(3.6)
] y lo sustituimos en la ecuación 3.6 tenemos:
−1
Y ( s ) = Yd ( s )[1 + Gfb( s)Gp( s)][1 + Gfb( s )Gp ( s )]
−1
Y ( s ) = Yd ( s )
(3.7)
Lo cual idealmente significaría tener un seguimiento perfecto de la señal de
referencia.
Esta técnica nos ofrece las siguientes ventajas:
1. Las características de prealimentación y las características de lazo cerrado se ajustan
sin depender una de otras.
2. El desempeño de seguimiento depende de Gff(s) y Gfb(s).
3. El rechazo a perturbaciones, la sensibilidad a los errores en el modelo, el márgen de
estabilidad y la sensibilidad en el ruido sólo dependen de Gfb
4. Gfb determina la característica del lazo de realimentación.
5. Gff afecta la función de transferencia en lazo cerrado entre la entrada de referencia
y la salida del sistema.
Sin embargo, esta técnica también presenta algunas desventajas como son:
1. El control por prealimentación
retroalimentación.
no
puede
reemplazar
al
control
por
2. La efectividad de un sistema prealimentado está limitado por el modelo matemático
que describe el sistema y la exactitud de los componentes involucrados. Las
inexactitudes pueden causar que el sistema prealimentado tenga una desviación en
estado estable.
42
CAPITULO 3
Control Prealimentado Neurodifuso Multivariable
3. La componente de control por prealimentación no puede compensar perturbaciones
inesperadas.
Como se mostró en la ecuación 3.7, se requiere del modelo inverso de la planta para
implementar el control retroalimentado, lo cual puede ser muy difícil de obtener si es que
este en realidad existe.
Actualmente con el avance del conocimiento, los sistemas neurodifusos nos ofrecen
una alternativa para representar una aproximación del modelo inverso de la planta, lo cual
nos permite seguir adelante con este esquema de control. La descripción de los sistemas
neurodifusos se presenta mas adelante en este capítulo.
Basándose en el esquema prealimentado de dos grados de libertad mostrado
anteriormente en la figura 3.1 y aplicándolo al esquema de control actual de la turbina de
gas visto en el capítulo anterior (ver figura 3.2), se forma el esquema propuesto para la
realización de este trabajo de tesis el cual se muestra en la figura 3.2.
Como se muestra en la figura 3.2 los controladores PI convencionales de velocidad,
potencia y temperatura se conservan (con su misma configuración retroalimentada) y se
añade un control prealimentado multivariable neurodifuso, para formar una estrategia de
control híbrida Retro-prealimentada.
El controlador prealimentado será del tipo MISO (multiples entradas y una salida)
donde las entradas al controlador serán las referencias de velocidad, potencia y temperatura
y la salida será la señal de control.
Control
PI
Neurodifuso
SP
PI
Velocidad
<
DEMANDA
PRIMARIA
SP
+
Demanda
Válvula
+
PI
Control
MW
<
Arranque
Ref. temp.
RPM
PI
PDC
Carga
Limitador
x Aceleración
Temp_Gases_Escape
Figura 3.2 Esquema de Control Propuesto aplicado al control de velocidad
potencia y temperatura de unidades turbogas.
Con este esquema de control se espera que la mayor aportación de la señal de
control sea proporcionada por el control prealimentado multivariable neurodifuso,
43
CAPITULO 3
Control Prealimentado Neurodifuso Multivariable
disminuyendo de esta manera la interacción entre los controladores PI´s, aportando estos
una señal complementaria de control utilizada para ajustes finos de control y rechazo de
perturbaciones.
3.3
Sistemas neurodifusos
Como se mencionó anteriormente para implementar el esquema de control
propuesto se necesita el modelo inverso de la planta, también se mencionó de la
complejidad de obtenerlo matemáticamente y de que una alternativa para obtenerlo es a
través de la aplicación de sistemas neurodifusos.
En la actualidad existen varios tipos de sistemas neurodifusos comerciales entre los
que se encuentran FALCON (Fuzzy Adaptive Learning Control Network) [20];
ARIC(Aproximate Reasoning based Intelligent Control)[20]; GARIC(Generalized
Aproximate Reasoning based Intelligent Control)[20]; NEFCON (Neuro Fuzzy Control)
[21]; NNDFR (Neural Network Driven Fuzzy Reasoning) [22]; FuNe (Fuzzy Network)
[23] y ANFIS (Adaptive Network based Fuzzy Inference System) [24].
Para el desarrollo de la tesis se utilizará ANFIS, debido a que es una clase de redes
adaptivas que son funcionalmente equivalentes a sistemas de inferencia difusos con un
método de auto sintonización (Sistemas de inferencia neurodifusos adaptivos). Otras
razones para su uso son la disponibilidad del software, ya que utiliza la misma plataforma
de programación (Matlab) empleada por el modelo de la unidad turbogas y se tiene
conocimiento previo de aplicaciones de ANFIS en otros proyectos realizados en el IIE.
Con el uso de un procedimiento híbrido de aprendizaje, ANFIS (puede construir un
mapeo de entrada – salidas basado en conocimiento humano en forma de reglas difusas si
– entonces (If_Then) y en pares de datos de entrada - salida estipulados. La arquitectura
ANFIS puede ser utilizada para modelar funciones no lineales, identificar componentes no
lineales en sistemas de control, predicción de series caóticas, aplicaciones de control
automático y procesamiento de señales. A continuación se describen los conceptos básicos
de los sistemas de inferencia difusos y de las redes neuronales, debido a que son las dos
técnicas que unen sus características y ventajas para generar los sistemas neurodifusos [24].
3.3.1
ANFIS
Para la realización de esta tesis se propone el uso de una clase de red adaptiva la cual es
funcionalmente equivalente a un sistema de inferencia difuso. La arquitectura propuesta es
llamada ANFIS (Sistema de Inferencia Difuso basado en Redes Adaptivas).
La arquitectura y reglas de aprendizaje de esta red adaptiva se describen en el anexo D.
3.3.1.1 Arquitectura ANFIS.
Por simplicidad asumiremos que el sistema de inferencia difuso bajo consideración
tiene 2 entradas x y y, una salida z. La base de reglas contiene 2 reglas difusas Si - entonces
del tipo Takagi y Sugeno [24].
44
CAPITULO 3
Control Prealimentado Neurodifuso Multivariable
Regla 1:
Si x es A1 & y es B1, entonces f1 = p1x + q1y + r1.
Regla 2:
Si x es A2 & y es B2, entonces f2 = p2x + q2y + r2.
La figura 3.3 ilustra el mecanismo de razonamiento para este modelo (tipo 3, ver anexo
D) y la arquitectura ANFIS equivalente a este razonamiento difuso es mostrado en la figura
3.4. como podemos observar ANFIS está compuesto por cinco capas, los nodos dentro de
una misma capa tienen funciones similares.
A3
A1
f1 = p1 x + q1 y + r1
w1
a1 b1
c1
a3 b3
X
c3
Y
f =
w1 f1 + w2 f 2
w1 + w2
= w1 f1 + w2 f 2
A2
A4
w2
a2 b2
c2
a4 b4
X
c4
y
x
f 2 = p 2 x + q 2 y + r2
Y
Figura 3.3 Mecanismo de razonamiento para un sistema TSK
capa 1
capa 2
capa 3
capa 4
A1
a1, b1, c1
x
x
A2
a2, b2, c2
A3
a3, b3, c3
Π
w1
N
w1
capa 5
y
p 1 , q 1, r 1
w1 f1
f
Π
w2
N
w2
p 2 , q 2, r 2
y
A4
a4, b4, c4
x
y
Figura 3.4 Diagrama del algoritmo ANFIS.
45
w2f2
CAPITULO 3
Control Prealimentado Neurodifuso Multivariable
Las funciones de cada nodo en la misma capa son descritos a continuación:
Capa 1: Cada nodo i en esta capa, es un nodo adaptivo con una función nodal. Para este
ejemplo esta capa tiene 4 nodos adaptivos (A1, A2, A3 Y A4).
O1,i = µ Ai (x )
para
i = 1,2,3 y 4
(3.8)
Donde x ó y es la entrada al nodo i, y Ai es la etiqueta lingüística (pequeño, mediano,
grande) asociada a este nodo, O1i es el grado de membresía. De Ai.
La función de membresía puede ser cualquier función parametrizada por ejemplo
trapezoidal, triangular, campana de gauss, etc, la siguiente función es la empleada en el
ejemplo (ver anexo D):
µ Ai ( x ) = max 0, min
x − ai ci − x
,
bi − a i c i − bi
(3.9)
Donde {ai, bi, ci} es el conjunto de parámetros, estos se conocen como parámetros
premisas o antecedentes.
Capa 2: Cada nodo en esta capa es un nodo fijo representado mediante un círculo,
etiquetado por una π, en el cual se realiza el producto de las señales de entrada.
O 2 ,i = ω i = µ A(1, 3 ) (x ) × µ A( 2 , 4 ) ( y ),
T).
i = 1, 2.
(3.10)
Cada salida del nodo representa la fuerza de disparo (activación) de la regla (Norma -
Capa 3: Cada nodo en esta capa es un nodo fijo representado mediante un círculo,
etiquetado por una N, en estos nodos se calcula la relación de la fuerza de disparo de la iésima regla respecto del total de fuerzas de disparo de las reglas.
ωi
O 3,i = ϖ i =
,
i =1 .
(3.11)
ω1 + ω 2
Las salidas de esta capa son llamadas fuerzas de activación o disparo normalizadas.
Capa 4: Cada nodo i en esta capa es un nodo adaptivo con una función nodal:
O 4 ,i = ϖ i f i = ϖ i ( p i x + q i y + ri )
(3.12)
Donde {pi, qi, ri} es el conjunto de parámetros, llamados parámetros consecuentes y
ϖ i es una fuerza normalizada proveniente de la capa 3.
46
CAPITULO 3
Control Prealimentado Neurodifuso Multivariable
Capa 5: Compuesto por un solo nodo, etiquetado con la letra Σ (sigma), el cual calcula
la salida total como la suma de todas las señales de entrada.
ϖ i fi =
O5 ,i =
i
i
ϖ i fi
ϖi
i
(3.13)
A través de estas 5 capas se construye una red adaptiva la cual es funcionalmente
equivalente a un sistema de inferencia difuso. Esta arquitectura ANFIS entonces puede
actualizar sus parámetros de acuerdo al procedimiento de actualización del gradiente
descendente (ver anexo D).
En resumen el procedimiento básico para construir un sistema neurodifuso, mediante la
combinación de sistemas neurodifusos (partiendo de los valores numéricos de las entradas,
la fusificacion, el sistema de inferencia difuso, la defusificacion) y redes neuronales
(aplicando los métodos de aprendizaje de gradiente descendente y mínimos cuadrados para
encontrar los mejores parámetros del sistema neurodifuso) se describe a continuación.
1. Definir el dominio de las variables de entrada para las funciones de membresía, de
acuerdo a los datos de entrenamiento
2. Definir el tipo y número de funciones de membresía para cada entrada (anexo C).
3. Inicializar los parámetros de las funciones de membresía.
4. Propagar todos los datos de entrenamiento por la red.
5. Aplicar el método de mínimos cuadrados, con la finalidad de encontrar los
parámetros de los consecuentes (anexo C).
6. Propagar nuevamente los patrones de entrenamiento para determinar el error.
7. Aplicar el método de aprendizaje de gradiente descendente para actualizar los
parámetros de las funciones de membresía (antecedentes) para cada patrón de
entrada (anexo C).
8. Una vez terminado el entrenamiento, verificar el comportamiento del sistema
neurodifuso (anexo C).
3.4
Diseño del Controlador Neurodifuso Multivariable
Como se mencionó anteriormente para poder implementar la estrategia de control
híbrida retro-prealimentada, necesitamos del modelo inverso de la planta, el cual será
representado por un sistema neurodifuso diseñado con ANFIS.
47
CAPITULO 3
Control Prealimentado Neurodifuso Multivariable
La metodología de diseño para implementar el control prealimentado será la siguiente:
Obtener los datos de entrenamiento.
Para obtener estos datos se utiliza el “Sistema para Desarrollo y Validación de
Algoritmos de Control para Turbinas de Gas, desarrollado en ambiente Simulink [19]
(ver anexo A). El cual básicamente realiza las funciones de simular la dinámica de la UTG,
el control lógico secuencial y el control regulatorio de acuerdo a como se describió en
capitulo anterior, implementando el esquema de control convencional que se mostró en la
figura 3.2. Los tres controles están basados en el control clásico Proporcional-Integrativo,
en donde las constantes de cada uno de los controles fueron encontradas aplicando el
método de Zeigler – Nichols, primero obteniendo una aproximación cercana a la deseada y
después ajustando las pequeñas variantes de cada control.
El entrenamiento del controlador ANFIS, requiere de un mapeo estático de las
variables del sistema UTG, por lo tanto es necesario realizar una simulación del sistema
UTG bajo las condiciones más optimas que el control convencional ofrece.
Ref.
Vel.
+
PI Vel.
-
+
+
Ref.
MW
Ref.
TGE
+
PI MW
-
<
SC
Vel.
UTG
MW
TGE
+
-
PI TGE
Datos de
entrenamiento
Entrada
Salida
Figura. 3.5 Obtención de los datos de entrenamiento
Las variables que se seleccionaron para generar los datos de entrenamiento son la
velocidad angular de la turbina de gas, la potencia (MW) generados por la turbinas de gas,
la temperatura de los gases de escape y la señal de control a la válvula de combustible.
Estos datos son almacenados en forma matricial para su posterior utilización. La forma en
que son almacenados estos datos se muestra en la figura 3.5, lo que interesa es obtener el
modelo inverso de la planta, por lo tanto las salidas de la planta (velocidad, MW, TGE) se
48
CAPITULO 3
Control Prealimentado Neurodifuso Multivariable
tomarán como las entradas para el sistema neurodifuso y la señal de entrada a la UTG
(señal de control) será la salida del sistema neurodifuso.
Estos datos de entrenamiento seleccionados se guardan en un archivo con formato
(.mat) para su posterior utilización en el editor grafico ANFIS de Matlab.
Normalización de los datos.
El entrenamiento de la red puede ser más eficiente si se emplean algunos pasos de
preprocesamiento de los datos, como puede ser el escalamiento o normalización de los
datos de las entradas y los de la salida, con mayor razón si estos presentan magnitudes muy
variados como es el caso de los datos de entrenamiento colectados anteriormente.
Para uniformizar estas magnitudes se empleó una transformación lineal T1, Esta
transformación lineal puede ser vista como un escalamiento y un desplazamiento de
coordenadas (figura 3.6).
Ymax
T1
y
T1-1
Ymin
Xmin
x
Xmax
Figura. 3.6 Mapeo lineal entre el dominio X de la variable física x y el universo de discurso normalizado
Y de la variable difusa y.
El mapeo desde el dominio de operación de las variables físicas hacia el rango de
operación normalizado se realiza a través de la transformación lineal T1, que se describe a
continuación.
T1: [Xmin, Xmax] → [Ymin, Ymax]
(x)
T1(x)= y = Y min +
Y max − Y min
(x − X min )
X max − X min
(3.14)
El mapeo desde el dominio de operación normalizado hacia el rango de operación de las
variables físicas se realiza a través de la transformación lineal inversa T1–1,que se describe
a continuación.
T1–1: [Ymin, Ymax] → [Xmin, Xmax]
49
CAPITULO 3
Control Prealimentado Neurodifuso Multivariable
(y)
T1–1(y)= x = X min +
X max − X min
( y − Y min )
Y max − Y min
(3.15)
donde:
x y y representan las variables físicas y normalizadas respectivamente.
X= [Xmin, Xmax] es el dominio de la variable física.
Y= [Ymin, Ymax] es el universo de discurso normalizado de la variable difusa.
Los rangos reales de las variables (velocidad, potencia, temperatura y señal de control)
y los rangos normalizados se resumen en la tabla 3.1.
Tabla 3.1. Rangos reales de la variables vs rangos normalizados
Variable
Rango real
Rango Normalizado
Velocidad
0-85 rps
0-1
Potencia
0-24000 kw
0-1
Temperatura
130-1000 °F
0-1
Señal de control
0-0.5
0-1
Los rangos reales de las variables (velocidad, potencia, temperatura y señal de control)
y los rangos normalizados se resumen en la tabla 3.1.
Diseño del sistema neurodifuso.
Para facilitar la programación del sistema neurodifuso, se utiliza el editor gráfico
ANFIS (anfisedit) de matlab [26], siguiendo el procedimiento mencionado en el anexo
B.
Después de haber realizado varios diseños de sistemas neurodifusos, con diferentes
combinaciones de características como: número y tipo de funciones de membresía de
entrada, tipo de salida, número de épocas de entrenamiento, método de inicialización y
generación del sistema de inferencia difuso, método de optimización para el entrenamiento,
etc. En base al error de entrenamiento se definió el sistema neurodifuso que representará el
control neurodifuso. Este índice de error depende de las características mencionadas
anteriormente y representa la diferencia entre los valores de salida de los datos de
entrenamiento y las salidas del sistema de inferencia difuso correspondiente a los mismos
datos de entrenamiento de entrada.
El sistema neurodifuso que representa al Control Neurodifuso Multivariable (CNM),
esta representado por un sistema difuso del tipo TSK (Takagi Sugeno Kan) de 3 entradas, 1
salida y 27 reglas generadas por las diferentes combinaciones de los antecedentes como lo
muestra la tabla 3.2. la estructura de este sistema neurodifuso se muestra en la figura 3.7.
Este sistema utiliza las siguientes definiciones:
50
CAPITULO 3
Entradas
Control Prealimentado Neurodifuso Multivariable
funciones
de membresia
trapezoidales
Reglas
w27
Salida
w 27
Velocidad
wi zi
Potencia
Temperatura
sc =
w1
w1
wi
Figura. 3.7 Estructura del sistema neurodifuso
•
Funciones de membresía de entrada:
a)
51
wi z
wi
CAPITULO 3
Control Prealimentado Neurodifuso Multivariable
b)
c)
Figura. 3.8. Funciones de membresía tipo trapezoidal para cada entrada. a) de velocidad, b) de
potencia, c) de temperatura
La utilización de funciones de pertenencia trapezoidal se debió a que el error de
entrenamiento generado con estas funciones fue menor, lo cual nos representa una mayor
aproximación al modelo inverso de la planta, además este tipo de función de membresía
reduce el tiempo computacional de entrenamiento. La función trapezoidal esta dada por:
x−a d −x
,1,
,0
trapezoide( x; a, b, c, d ) = max min
donde a < b < c < d (3.16)
b−a d −c
D).
siendo a, b, c, d los vértices del trapecio tal como lo muestra la figura 3.9 (véase anexo
1
a
b
c
d
x
Figura. 3.9 Función de pertenencia trapezoidal
52
CAPITULO 3
•
Control Prealimentado Neurodifuso Multivariable
Inferencia basada en reglas individuales, la tabla 3.2 muestra la base de reglas, estas reglas
son generadas por la combinación de las entradas, como tenemos 3 entradas (velocidad,
potencia y temperatura) y cada una esta compuesta por tres conjuntos difusos (baja, media y
alta) esto nos da una combinación de 27 reglas.
Tabla 3.2. Base de reglas del sistema neurodifuso
Re
gla
1
Condi
cional
Si
Antecedente1
Antecedente2
Antecedente3
Condici Consecuente
onal
Entonces z = p x + q
Velocidad baja y
Potencia baja y
Temp. baja
2
Si
Velocidad baja y
Potencia baja y
Temp. media
Entonces
3
Si
Velocidad baja y
Potencia baja y
Temp. alta
Entonces
4
Si
Velocidad baja y
Potencia media y
Temp. baja
Entonces
5
Si
Velocidad baja y
Potencia media y
Temp. media
Entonces
6
Si
Velocidad baja y
Potencia media y
Temp. alta
Entonces
z 6 = p 6 x + q 6 y + r6
7
Si
Velocidad baja y
Potencia alta y
Temp. baja
Entonces
z 7 = p 7 x + q 7 y + r7
8
Si
Velocidad baja y
Potencia alta y
Temp. media
Entonces
z 8 = p8 x + q8 y + r8
9
Si
Velocidad baja y
Potencia alta y
Temp. alta
Entonces
z 9 = p 9 x + q 9 y + r9
10
Si
Velocidad media y Potencia baja y
Temp. baja
Entonces
z10 = p10 x + q10 y + r10
11
Si
Velocidad media y Potencia baja y
Temp. media
Entonces
12
Si
Velocidad media y Potencia baja y
Temp. alta
Entonces
13
Si
Velocidad media y Potencia media y
Temp. baja
Entonces
z11 = p11 x + q11 y + r11
z12 = p12 x + q12 y + r12
z13 = p13 x + q13 y + r13
14
Si
Velocidad media y Potencia media y
Temp. media
Entonces
15
Si
Velocidad media y Potencia media y
Temp. alta
Entonces
16
Si
Velocidad media y Potencia alta y
Temp. baja
Entonces
z16 = p16 x + q16 y + r16
17
Si
Velocidad media y Potencia alta y
Temp. media
Entonces
z17 = p17 x + q17 y + r17
18
Si
Velocidad media y Potencia alta y
Temp. alta
Entonces
z18 = p18 x + q18 y + r18
19
Si
Velocidad alta y
Potencia baja y
Temp. baja
Entonces
z19 = p19 x + q19 y + r19
20
Si
Velocidad alta y
Potencia baja y
Temp. media
Entonces
z 20 = p 20 x + q 20 y + r20
21
Si
Velocidad alta y
Potencia baja y
Temp. alta
Entonces
22
Si
Velocidad alta y
Potencia media y
Temp. baja
Entonces
23
Si
Velocidad alta y
Potencia media y
Temp. media
Entonces
z 21 = p 21 x + q 21 y + r21
z 22 = p 22 x + q 22 y + r22
z 23 = p 23 x + q 23 y + r23
24
Si
Velocidad alta y
Potencia media y
Temp. alta
Entonces
25
Si
Velocidad alta y
Potencia alta y
Temp. baja
Entonces
26
Si
Velocidad alta y
Potencia alta y
Temp. media
Entonces
z 26 = p 26 x + q 26 y + r26
27
Si
Velocidad alta y
Potencia alta y
Temp. alta
Entonces
z r = p 27 x + q 27 y + r27
y + r1
z 2 = p 2 x + q 2 y + r2
z 3 = p3 x + q3 y + r3
1
1
1
z 4 = p 4 x + q 4 y + r4
z 5 = p5 x + q5 y + r5
z14 = p14 x + q14 y + r14
z15 = p15 x + q15 y + r15
z 24 = p 24 x + q 24 y + r24
z 25 = p 25 x + q 25 y + r25
En el sistema neurodifuso ANFIS, por su estructura en forma de red neuronal aplica
un método de aprendizaje híbrido, es decir por medio del método de gradiente descendente
53
CAPITULO 3
Control Prealimentado Neurodifuso Multivariable
calcula los parámetros de los antecedentes y aplicando el método de mínimos cuadrados
determina los parámetros de los consecuentes.
•
Implicación mínimo de mandani, Norma-T producto algebraico y norma-S máximo.
•
Defusificación por promedio ponderado, Es decir la salida del sistema difuso TSK
está dada por:
r
O5 , r =
ϖ r zr
r =1
r
(3.17)
ϖr
r =1
Donde:
(3.18)
z r = p r x + q r y + rr
Implementar el CNM al sistema de control.
Una vez construido el sistema neurodifuso que representa el modelo inverso de la
planta, procedemos a incorporarlo al sistema para desarrollo y validación de los algoritmos
de control para turbinas de gas, desarrollado en ambiente simulink (figura 3.10).
Control
neurodifuso
+
Ref.
Vel.
PI Vel.
-
+
+
+
Ref.
MW
PI MW
-
Ref.
TGE
<
+
-
+
+
Vel.
sc
UTG
MW
TGE
PI TGE
Figura. 3.10 Implementación del sistema neurodifuso al esquema de control
Las entradas al controlador neurodifuso son las referencias de velocidad, potencia y
temperatura, y su salida será la señal de control de la cual se espera que aporte la mayor
parte de la señal de control total.
54
CAPITULO 3
Control Prealimentado Neurodifuso Multivariable
Probar y ajustar los controladores
Él ultimo paso del diseño es probar el CNM en conjunto con los controladores PI
existentes, estos controladores PI fueron ajustados para trabajar como controladores
independientes y aportar gran parte de la señal de control, con el esquema propuesto estos
controladores aportan una señal de control menor (complementaria) dedicada para rechazar
disturbios y realizar ajustes finos en la señal de control, por lo tanto es necesario reajustar
los parámetros de estos controladores para obtener el mejor desempeño de ellos.
3.5
Pruebas del CNM con ajuste de los controladores PI
Después de haber diseñado el sistema neurodifuso y de haber implementado el esquema
de control propuesto en el sistema para desarrollo y validación de algoritmos de control
para turbinas de gas, se procede a evaluar los resultados, comparando el desempeño del
esquema propuesto implementado con el controlador prealimentado neurodifuso
multivariable contra el esquema de control actual implementado con algoritmos de control
convencionales PI.
El desempeño de los esquemas de control se evalúan realizando las siguientes pruebas:
a) Interacción entre controladores,
b) Pruebas de seguimiento y,
c) Rechazo a disturbios.
El análisis de esta pruebas se presentan en el siguiente capítulo.
3.6
Conclusiones
Como se observo en el capitulo anterior, el esquema de control convencional
utilizado en las UTG, tiene un comportamiento aceptable, sin embargo también presenta
algunas desventajas. Lo cual da la posibilidad de partir del esquema de control
convencional para aprovechar sus beneficios y mediante la combinación de otra técnica de
control, como es el control prealimentado lograr mejores resultados y disminuir las
desventajas presentadas anteriormente.
La principal limitante para implementar la estrategia con el control prealimentado,
es que se requiere del modelo inverso de la planta, en este caso el de la turbina de gas, el
cual es muy grande y complejo, por lo tanto este modelo inverso es muy difícil o imposible
de obtener.
Actualmente con el avance del conocimiento, los sistemas neurodifusos ofrecen una
alternativa para representar una aproximación del modelo inverso de la planta. Para lograr
esto se utilizara ANFIS, debido a que es una clase de red adaptiva funcionalmente
equivalente a un sistema de inferencia difuso con un método de auto sintonización.
55
CAPITULO 4
Evaluación y Análisis de Resultados
EVALUACIÓN Y ANÁLISIS DE
RESULTADOS
4.1
Introducción.
En este capítulo se presentan las simulaciones y pruebas realizadas a los esquemas
de control vistos en el capítulo 2 (esquema típico de control basado en PI´s convencionales)
y en el capítulo 3 (esquema propuesto basado en un controlador prealimentado
neurodifuso).
Las pruebas fueron realizadas en el sistema para desarrollo y validación de
algoritmos de control para turbinas de gas [19], desarrollado en la Gerencia de Control e
Instrumentación del IIE. Las pruebas que se realizaron son: la afectación a la señal de
control provocada por la interacción de los controladores, evaluación del comportamiento
de los esquemas de control a través de índices de error, pruebas de seguimiento y pruebas
de rechazo a disturbios.
56
CAPITULO 4
4.2
Evaluación y Análisis de Resultados
Ambiente de Pruebas
La realización de pruebas se llevó a cabo mediante el uso del “Sistema para Desarrollo y
Validación de Algoritmos de Control para Turbinas de Gas”, desarrollado en ambiente
Simulink . Este ambiente de prueba fue desarrollado en MATLAB versión 6.0, utilizando
un lenguaje modular ofrecido por la herramienta de Matlab llamada Simulink para
facilitar el entendimiento y modificación del Sistema para Desarrollo y Validación de
Algoritmos de Control para Turbinas de Gas.
Las funciones que realiza este sistema son las siguientes.
1) Simular la dinámica de la turbina de gas, a partir del modelo matemático de la misma,
se generan las variables principales necesarias para el sistema de control, como son: la
velocidad angular del rotor, la potencia generada, la temperatura de los gases de escape
y la presión de descarga del compresor.
2) Control Lógico Secuencial. Cuenta con un sistema de secuenciamiento de arranque, que
permite efectuar las etapas y permisivos mínimos necesarios para llevar a cabo el
arranque de la unidad turbogas.
3) Control Regulatorio. Tiene un sistema de control simplificado que permite regular la
velocidad, potencia generada y temperatura de los gases de escape durante las
diferentes etapas de operación de la unidad turbogas. Además, éste modelo permite
sustituir el controlador seleccionado basado en un control clásico, por algún otro; como
es el caso de los controladores basados en lógica difusa, redes neuronales, neurodifusos,
algoritmos genéticos o evolutivos.
Para realizar las pruebas del Sistema Turbogas, fue necesaria la implementación de la
sección secuencial lógica, así como de la sección del control, donde se involucraron los tres
controles, el de Potencial, Velocidad y Temperatura. Los tres controles se basaron en el
control clásico Proporcional -Integrativo – Derivativo, en donde las constantes de cada uno
de los controles fueron encontradas aplicando el método de Zeigler – Nichols, teniendo una
aproximación cercana a la deseada y solamente ajustando las pequeñas variantes de cada
control, la implementación fue hecha mediante el control Proporcional - Integrativo para
los tres casos. Una descripción más detallada de este sistema se presenta en el anexo A.
4.3
Pruebas del esquema propuesto vs esquema de control convencional.
Una vez diseñado el Controlador Neurodifuzo Multivariable e implementado en el
sistema para desarrollo y evaluación de algoritmos de control, se procede a realizar las
siguientes pruebas.
a)
Interacción entre los controladores.
b)
Pruebas de seguimiento.
57
CAPITULO 4
Evaluación y Análisis de Resultados
c)
Rechazo a disturbios
4.3.1
Interacción entre los controladores
Como se mencionó en el capítulo 3, una de las desventajas más relevantes que se
generan con el esquema actual de control, es el uso de controladores independientes
(control/supervisor) los cuales actúan solo sobre una válvula de control, implicando una
fuerte interacción entre los mismos. De modo que no permite realizar ajustes finos en un
controlador sin que estos ajustes afecten el desempeño de los demás controladores. Esta
limitante tiene inferencia directa sobre el seguimiento de las curvas de referencia.
A continuación se presentan las tres gráficas mostradas en el capítulo 3: Respuestas de
velocidad (figura 4.1), de potencia (figura 4.2), y de temperatura de gases de escape (figura
4.3), con la finalidad de recordar la interacción entre los controladores, estas gráficas
presentan la variante de que también se ha introducido la respuesta obtenida con el esquema
de control propuesto, con el objetivo de poder realizar una análisis comparativo entre los
dos esquemas de control.
4
5
6
7
3
2
1
Figura 4.1 Gráfica de la velocidad angular de la TG.
58
8
CAPITULO 4
Evaluación y Análisis de Resultados
4
5
6
7
8
3
2
1
Figura 4.2 Gráfica de la temperatura de los gases de escape de la TG.
6
7
8
4
1
2
5
3
Figura 4.3 Gráfica de la potencia generada de la TG.
59
CAPITULO 4
Evaluación y Análisis de Resultados
En el capítulo 3 se explicó detalladamente la interacción entre los controladores. En este
capítulo se muestra la tabla 4.1 la cual resume los eventos enumerados en las gráficas,
estos nos sirven de guía para describir la interacción que existe entre los controladores.
Evento
1-2
2-3
3-4
4-5
5-6
6-7
7-8
Tabla 4.1 Puntos de interacción entre los controladores
Descripción
Etapa de arranque, el PI de velocidad se encuentra operando. Este empieza a
operar después de la velocidad de ignición.
Etapa de arranque, el PI de temperatura toma el control hasta regular la
temperatura. Durante este período se pierde el seguimiento de la curva de
referencia de velocidad.
Etapa de arranque, el PI de velocidad retoma el control y el seguimiento de la
curva de referencia de velocidad hasta alcanzar la velocidad de sincronismo,
donde cede el control al PI de potencia.
Etapa de generación, el PI de potencia es activado, en este periodo se encarga de
llevar a demanda mínima a la UTG.
Etapa de generación, el PI de potencia en este período se encarga de llevar a
demanda máxima a la UTG.
Etapa de generación, el PI de temperatura toma el control hasta regular la
temperatura. La potencia es limitada por esta sobre- temperatura.
Etapa de generación, el PI de potencia en este período se encarga de llevar a
demanda mínima a la UTG.
Como se observa en las figuras anteriores, las respuestas obtenidas con los dos esquemas
de control son similares, sin embargo, haciendo acercamientos en los diferentes puntos
mencionados en la tabla 4.1 se puede observar como las respuestas obtenidas con el
esquema de control propuesto mejoran el comportamiento del esquema de control
convencional. Estas gráficas que muestran los acercamientos se presentan a continuación.
Las primeras dos gráficas muestran el comportamiento de la velocidad angular de la turbina
de gas mientras se encuentra operando el controlador de velocidad. Después se muestran el
comportamiento de la temperatura de gases de escape cuando esta sobrepasa o se acerca al
límite de temperatura impuesto por el fabricante, y finalmente se muestran las gráficas del
comportamiento de la potencia cuando opera el control de potencia.
Como se observa en la figura 4.4 el control de velocidad se activa una vez que se ha
alcanzado las 1700 rpm, presentándose inmediatamente la ignición que inicia la combustión
y abre la válvula de combustible. Como se observa los dos controladores tienen un buen
seguimiento inicial, el cual se va perdiendo conforme se va incrementando la demanda de
combustible hasta que la temperatura de gases de escape sobrepasa el límite impuesto por el
fabricante.
60
CAPITULO 4
Evaluación y Análisis de Resultados
2
1
Figura 4.4 Gráfica de la velocidad angular de la TG en el primer período de control del PI de velocidad
Continuando con el control de velocidad, durante la etapa de arranque en la figura
4.5 se observa como el regulador de velocidad retoma el control después de que la
temperatura de los gases de escape ha sido regulada, y este lleva a la UTG hasta la
velocidad de sincronismo. En términos generales se observa que el seguimiento
proporcionado por el esquema de control propuesto es mejor que el generado por el
esquema de control actual. En este lapso de tiempo ocurre un evento importante el cual es
necesario analizar, como se puede observar a la velocidad de 4845 rpm aproximadamente,
se presentan oscilaciones en la respuesta de velocidad de los dos esquemas de control, esto
es debido a que a esta velocidad se cierran las válvulas de sangrado del compresor,
provocando una sobre velocidad, derivada del incremento de flujo de aire, ambos esquemas
de control tratan de corregir este disturbio natural, pero enseguida se presenta la apertura de
los álabes guía, provocando nuevamente un incremento de la velocidad. Como se observa
en las gráfica el esquema de control propuesto, regula mejor y más rápido estos dos
disturbios presentados durante la etapa de arranque.
61
CAPITULO 4
Evaluación y Análisis de Resultados
4
3
Figura 4.5 Gráfica de la velocidad angular de la TG en el segundo periodo de control del PI de vel.
Las figuras 4.6 y 4.7 nos muestra las etapas en las cuales el control supervisor de
temperatura de gases de escape toma el control para regular la temperatura y evitar que
esta sobrepase el límite impuesto por el fabricante.
Particularmente la figura 4.6 muestra la regulación de temperatura durante la etapa de
arranque (puntos 2-3), como se aprecia en la parte inferior izquierda, en un principio,
tanto la respuesta del control convencional como la del propuesto sobrepasan este límite,
debido a que en este momento el control de velocidad incrementa la demanda de
combustible, provocando que aumente la temperatura. Sin embargo después de este
transitorio se puede observar como la respuesta del esquema de control propuesto regula
la temperatura ajustándose a la curva de referencia, mientras el esquema de control
convencional no alcanza a tener una buena regulación, como ya se mencionó esto puede
provocar daños a la UTG.
La figura 4.7 muestra la regulación de temperatura durante la etapa de generación, como
se puede apreciar en términos generales con el esquema de control propuesto se
alcanza a operar más cerca de la temperatura límite impuesta por el fabricante, lo cual
permitirá incrementar la potencia generada por la UTG.
62
CAPITULO 4
Evaluación y Análisis de Resultados
3
2
Figura 4.6 Gráfica de la TGE de la TG durante la etapa de arranque.
6
7
Figura 4.7 Gráfica de la TGE de la TG durante la etapa de generación.
63
CAPITULO 4
Evaluación y Análisis de Resultados
Por último analizamos la etapa de generación, como ya lo mencionamos después de
que el control de velocidad lleva a la UTG a la velocidad de sincronismo, este cede el
control al regulador de potencia, el cual se encarga de generar la potencia demandada por el
operador. Primero llevándolo a carga mínima, donde no se presenta ningún problema para
cualquiera de los dos controladores, y después a carga máxima, las siguientes figuras
muestran el comportamiento durante esta etapa.
Como se observa en la figura 4.8, el esquema de control propuesto proporciona
claramente un mejor seguimiento de la curva de referencia, desde carga mínima hasta el
máximo de potencia producido por la UTG, en comparación con el seguimiento producido
por el esquema actual de control.
En la figura 4.9 se observa la potencia máxima generada por la UTG, cabe recordar
que la generación de potencia está limitada por la habilidad del sistema de control para
regular la temperatura lo más cerca posible del límite de temperatura impuesta por el
fabricante. Como se vio anteriormente el esquema de control propuesto mostró ser más
eficaz en este punto, por lo tanto permite una generación adicional de aproximadamente
100 Kw. Esto representa una clara ventaja sobre el esquema de control convencional.
6
5
Figura 4.8 Gráfica del seguimiento de la referencia de potencia.
64
CAPITULO 4
Evaluación y Análisis de Resultados
7
6
Figura 4.9 Gráfica de la potencia máxima generada.
Como se observó cualitativamente en todas las gráficas anteriores el esquema de
control propuesto, genera un mejor comportamiento en cuanto a: regulación de disturbios,
seguimiento de curvas de referencia, mejor regulación de la temperatura de gases de
escape, mayor generación de potencia.
Estas mejoras son consecuencia de que ahora el Control Neurodifuso Multivariable
Prealimentado (CNMP) aporta la mayor contribución a la señal de control, mientras que los
controladores PI’s aportan una señal complementaria, utilizada para realizar ajustes finos a
la señal de control. Al disminuir la contribución de los PI´s a la señal de control,
lógicamente también disminuye la afectación negativa provocada por la interacción entre
estos. Permitiendo de esta manera una mejor regulación y seguimiento de curvas de
referencia.
La figura 4.10 nos muestra las señales de control proporcionadas por el control
neurodifuso prealimentado y por la combinación de los PI´s retroalimentados. Como se
aprecia en la figura la señal de control proporcionada por el CNMP es mayor en todo
instante de tiempo y con cambios más suaves en su magnitud, mientras que la señal
proveniente de los controladores retroalimentados es menor, y esta presenta en algunas
secciones cambios bruscos provocados por la interacción de los controladores.
65
CAPITULO 4
Evaluación y Análisis de Resultados
Figura 4.10 Señales de control generadas por el esquema de control propuesto
La gráfica 4.11 muestra las señales de control del esquema propuesto y del esquema
convencional, como se observa estas son muy similares en cuanto a magnitud y
oscilaciones provocadas por la interacción entre los controladores PI’s retroalimentados.
Figura 4.11 Señales de control de los esquemas de control.
66
CAPITULO 4
4.3.2
Evaluación y Análisis de Resultados
Evaluación del sistema de control mediante índices de comportamiento
Como los sistemas de control son dinámicos, se puede evaluar su comportamiento
en función de términos de respuesta transitoria ante determinadas entradas, tales como
escalón, rampa, etc., o se pueden dar especificaciones en términos de un índice de
comportamiento [26,27]. Un índice de comportamiento es un número que indica el grado
de beneficio del sistema, es decir es una medida cuantitativa del comportamiento, que
indica la desviación respecto al comportamiento ideal. La evaluación de un sistema se
puede considerar aceptable si los valores de los índices de comportamiento son un mínimo
o un máximo.
En la literatura se han propuesto varios índices de comportamiento basados en el
error, que son integrales de alguna función de la salida del sistema en sí, con la entrada
deseada. El objetivo de esta sección es el evaluar el desempeño del control propuesto y el
convencional mediante la aplicación de los siguientes índices de error.
Los índices de error utilizados más comúnmente son la Integral Absoluta del Error
(IAE) y la Integral del Tiempo por el valor Absoluto del Error (ITAE) cuyas formulas son:
IAE =
ITAE
=
t
0
t
0
e dt
(4.1)
t e dt
(4.2)
Un sistema evaluado con el criterio IAE, es un sistema con razonable
amortiguamiento y satisfactoria característica de respuesta transitoria. Para el ITAE, un
error grande en la respuesta transitoria pesa poco y los errores que se presentan más tarde
son penalizados severamente. El esquema de control que presente el valor mínimo al ser
evaluados con el IAE y el ITAE representará el mejor sistema.
Como se vio en la sección anterior el control de las variables (velocidad, potencia y
temperatura) se da por lapsos de tiempo (es decir sólo puede operar un controlador a la vez
y estos se alternan el control de la UTG por instantes de tiempo). Así que los índices de
error se cuantificaron sólo en estos lapsos de tiempo para cada controlador.
La cuantificación de estos índices también nos aporta una medición directa del
seguimiento de las curvas de referencia que generan los esquemas de control analizados.
67
CAPITULO 4
Evaluación y Análisis de Resultados
Tiempo (seg.)
Tiempo (seg.)
Figura. 4.12 Índices de error IAE e ITAE de las respuestas de velocidad
! "
!
!
!
#
$
Tabla 4.2 índices de error de la velocidad angular de la TG
Esquema de Control
PI convencional
Esquema de control propuesto
#
IAE
ITAE
1
0.2160
1
0.2484
%
&
#
'
%
#
(
!
#
'
#
!
)
! "
%
%
!
!
#
68
&
#
CAPITULO 4
Evaluación y Análisis de Resultados
Tiempo (seg.)
Tiempo (seg.)
Figura. 4.13 Índices de error IAE e ITAE de las respuestas de temperatura de gases de escape
Tabla 4.3 Índices de error de la temperatura de gases de escape de la TG
Esquema de Control
PI convencional
Esquema de control propuesto
IAE
1
0.1537
ITAE
1
0.176
*
+, #
#
'
!
!
%
!
-- . /
#
%
!
Tiempo (seg.)
Tiempo (seg.)
Figura. 4.14 Índices de error IAE e ITAE de las respuestas de la potencia generada.
Tabla 4.4 Índices de error de la potencia generada por la TG
Esquema de Control
PI convencional
Esquema de control propuesto
IAE
1
0.03
69
ITAE
1
0.066
CAPITULO 4
Evaluación y Análisis de Resultados
En términos generales se observó cómo para todos los casos analizados, los índices
de error generados por el esquema de control propuesto son menores que los generados por
el esquema control convencional, remarcando los resultados obtenidos en la sección
anterior. Por ultimo en las figura 4.15 y 4.16, se muestran las gráficas del error de
seguimiento de la velocidad y de la potencia, en ambas gráficas se observa claramente
como el error del control propuesto es menor, traduciéndose en un mejor seguimiento de las
curvas de referencia.
Seguimiento de
Velocidad
Figura. 4.15 Gráfica del error de seguimiento de la velocidad.
70
CAPITULO 4
Evaluación y Análisis de Resultados
Figura. 4.16 Gráfica del error de seguimiento de la potencia.
4.3.3
Rechazo a disturbios
Para realizar esta prueba se seleccionó y se implementó en el modelo un disturbio
real que es muy representativo del proceso y ocurre durante la operación de la turbina de
gas, este disturbio es conocido como rechazo de carga. Este se origina cuando súbitamente
se abre el Interruptor principal del Generador (IPG), estando la unidad en modo de
generación de potencia eléctrica.
El IPG puede abrirse súbitamente, por alguna de las siguientes causas:
a) Falla en el BUS de salida,
b) Falla del interruptor del BUS de salida y
c) Apertura accidental del IPG (error de operación)
En cualquier caso, el efecto consiste en un incremento muy rápido de la velocidad
ocasionado por la aceleración excesiva debido al alto valor de demanda a la válvula de
combustible (en el momento de la apertura del IPG), lo que produciría el paro de la unidad
si se alcanza el límite de disparo por sobre-velocidad (5480 rpm) o por baja velocidad. Es
claro pensar que a mayor carga generada es mayor el aceleramiento en la velocidad de la
turbina una vez desacoplada del generador. Esta prueba se realizó con generación máxima
de potencia de la UTG con la finalidad de probar un caso extremo.
71
CAPITULO 4
Evaluación y Análisis de Resultados
Figura. 4.17 Respuestas de la potencia generada ante el disturbio
En la figura 4.17 se observa el efecto sobre la generación de potencia que ocurre
cuando el interruptor de generador es abierto, la potencia cae súbitamente hasta los cero
megawatts, en ambos esquemas de control.
En el esquema de control convencional la estrategia que se toma para regular esta
velocidad y evitar el paro de la unidad es el agregar un controlador supervisor de velocidad
(CSV), basado también en un algoritmo PI convencional. Este CSV lógicamente también
presenta las desventajas de un control convencional, además de que el adicionar otro
controlador independiente aumenta la interacción entre los controladores, por la
manipulación de la válvula de control.
Con el esquema de control propuesto se logró que este disturbio sea controlado, sin
adicionar el control supervisor de velocidad, tal como se observa en la Fig. 4.18, además
este disturbio es rechazado más rápidamente y con oscilaciones de menor magnitud que con
el CSV.
72
CAPITULO 4
Evaluación y Análisis de Resultados
Figura. 4.18 Respuestas de la velocidad ante el disturbio
La figura 4.19 muestra la señal de control generada por estos dos esquemas de
control para rechazar el disturbio.
Figura. 4.19 Salida de los controladores ante rechazo a disturbio
73
CAPITULO 4
Evaluación y Análisis de Resultados
Un evento que se observa en la gráfica 4.19, en ambos controladores, es el de saturación,
este se presenta cuando la señal de salida del controlador es mayor o menor a la posición
máxima o mínima que físicamente puede tomar la válvula. La saturación puede ocasionar
inestabilidad para tiempos de saturación prolongados, pero en este caso el período de
saturación es de poca duración en ambos controladores, y este todavía es menor para la
señal de salida del esquema de control propuesto.
4.4
Conclusiones
•
Con el uso del controlador prealimentado neurodifuso multivarianle se logró
disminuir la influencia de la interacción entre los controladores (controles
convencionales PI’s), ya que ahora estos sólo proporcionan una señal
complementaria utilizada para realizar ajustes finos y rechazar disturbios, mientras
la mayor aportación de la señal de control es suministrada por el controlador
neurodifuso multivariable.
•
Como se observó en los resultados, gracias al esquema de control propuesto el
seguimiento de las curvas de referencia fue mejorado, debido al uso del control
prealimentado neurodifuso multivariable, permitiendo una mejor regulación de la
temperatura en relación con los limites impuestos por el fabricante, de esta manera
aumenta su eficiencia y potencia de salida, y evita el desgaste prematuro de la
unidad por sobre temperaturas.
•
Con el mismo control prealimentado multivariable neurodifuso se logró controlar el
disturbio generado por el rechazo de carga, sin necesidad de utilizar un controlador
adicional.
74
CAPITULO 5
CONCLUSIONES
CONCLUSIONES
5.1
Introducción.
En este trabajo de tesis se presentó el diseño y validación de un sistema de control
prealimentado neurodifuso multivariable basado en técnicas de control inteligente, para su
incorporación al sistema de control de velocidad, potencia y temperatura de gases de escape
de una unidad turbogas.
Se comparó su desempeño con el sistema de control convencional basado en
controladores del tipo PI.
En esta sección se presentan las conclusiones derivadas de estas comparaciones del
esquema de control propuesto y del esquema convencional, y se recuerda la problemática
que motivó a la realización del esquema propuesto de control.
75
CAPITULO 5
5.2
CONCLUSIONES
Problemática
El sistema de control de las unidades turbogas está basado en algoritmos de control
convencionales del tipo PI. Este esquema de control es destinado para tareas de regulación
y rechazo a perturbaciones, y no para seguimiento de puntos de referencia.
Los controladores actúan todos sobre una sola válvula de control, lo cual representa
una fuerte interacción entre los mismos, por ejemplo un ajuste en los parámetros del
algoritmo del PI digital de temperatura, puede mejorar su desempeño pero también puede
afectar el desempeño del control de velocidad o el de potencia.
La turbina de gas presenta un comportamiento no lineal y variante en el tiempo,
principalmente en la etapa de arranque donde se presentan varios disturbios importantes.
Actualmente los controladores utilizados en los lazos de control de las turbinas son lineales
los cuales son sintonizados para un punto de operación especifico y son conservados así por
tiempo indefinido
5.3
Conclusiones
En este trabajo de tesis se diseño y desarrollo un controlador prealimentado
neurodifuso multivariable, basado en técnicas de control inteligente. Este controlador se
incorporo al sistema de control de velocidad, potencia y temperatura de una UTG,
generando un nuevo esquema de control. Con el uso del nuevo esquema de control se
alcanzaron los siguientes beneficios:
•
Se logró disminuir la influencia de la interacción entre los controladores (controles
convencionales PI’s), ya que ahora estos sólo proporcionan una señal
complementaria utilizada para realizar ajustes finos y rechazar disturbios, mientras
la mayor aportación de la señal de control es suministrada por el controlador
neurodifuso multivariable. Este logro implica una mejor regulación en cualquiera de
las variables controladas (velocidad, temperatura, potencia) sin que esta afecte a las
otras variables.
•
Como se observó en los resultados, gracias al esquema de control propuesto el
seguimiento de las curvas de referencia fue mejorado, debido al uso del control
prealimentado neurodifuso multivariable, permitiendo una mejor regulación de la
temperatura en relación con los limites impuestos por el fabricante. Esto se traduce
en beneficios económicos y de seguridad del personal, como pueden ser un aumento
en la potencia de salida de la UTG, reducir los mantenimientos correctivos de la
unidad y evitar el desgaste prematuro de la unidad por sobre temperaturas.
•
Con el mismo control multivariable neurodifuso se logró controlar el disturbio
generado por el rechazo de carga, sin necesidad de utilizar un controlador adicional
como ocurre con el esquema de control convencional, lo cual evita un incremento
de la interacción entre los controladores.
76
CAPITULO 5
5.4
CONCLUSIONES
Aportaciones
También el desarrollo de este trabajo de tesis proporciona las siguientes
aportaciones:
•
Se revisó y complementó (con la integración del controlador multivariable
neurodifuso) el Sistema para Desarrollo y Validación de Algoritmos de Control para
Turbinas de Gas.
•
Este trabajo de tesis aporta el diseño y simulación de técnicas de control inteligente
basado en sistemas neurodifusos multivariables, aplicado a procesos de generación.
•
El desarrollo de esta tesis y los logros alcanzados fortalecen la línea de
investigación del grupo de control de la Gerencia de Control e Instrumentación del
IIE, en cuanto a la aplicación de técnicas inteligentes de control en sistemas de
generación.
•
Se publicó el artículo “Control Neurodifuso Aplicado al Control de Velocidad,
Potencia y Temperatura de Unidades Turbogas” en la 17ª reunión de verano de
potencia, aplicaciones industriales y exposición industrial. (RVP-AI/2004),IEEE,
Acapulco. Guerrero (anexo D).
5.5
Trabajos futuros.
•
Redacción y publicación de un artículo nacional o internacional con los resultados
finales.
•
Validación en laboratorio con controladores industriales, es decir, implementar los
algoritmos del esquema de control actual en un microprocesador industrial para
turbinas de gas y realizar pruebas en tiempo real con el simulador de la turbina de
gas.
77
ANEXO A
AMBIENTE DE PRUEBA
AMBIENTE DE PRUEBA
A.1 Introducción.
En este apéndice se presenta el sistema para desarrollo y validación de algoritmos
de control para turbinas de gas, desarrollado en ambiente Simulink [19]. Se describen los
principales bloques que lo conforman, su programación , su operación y pruebas del
algoritmo de control basado en PI convencional.
78
ANEXO A
AMBIENTE DE PRUEBA
A.2 Sistema de prueba
Las funciones que realiza el sistema son las siguientes (figura A.1).
a) Simula la dinámica de la turbina de gas, A partir del modelo matemático de la misma,
se generan las variables principales necesarias para el sistema de control, como son: la
velocidad angular del rotor, la potencia generada, la temperatura de los gases de escape
y la presión de descarga del compresor,
b) Control Lógico Secuencial. Cuenta con un sistema de secuenciamiento de arranque, que
permita efectuar las etapas y permisivos mínimos necesarios para llevar a cabo el
arranque de la unidad turbogás y,
c) Control Regulatorio. Tiene un sistema de control simplificado que permita regular la
velocidad, potencia generada y temperatura de los gases de escape durante las
diferentes etapas de operación de la unidad turbogás. Además éste modelo permite el
sustituir el controlador seleccionado basado en un control clásico, por algún otro
propuesto por el diseñador.
Secuencia
lógica
Unidad
Turbogás
Control
Regulatorio
Figura A.1 Diagrama a bloques de la operación de la UTG.
Para realizar las pruebas del Sistema Turbogás, fue necesaria la complementación
de la sección secuencial lógico, así como de la sección del control, donde se involucraron
los tres controles, el de Potencial, Velocidad y Temperatura. Los tres controles se basaron
del control clásico Proporcional -Integrativo – Derivativo, en donde las constantes de cada
uno de los controles fueron encontradas aplicando el método de Zeigler – Nichols, teniendo
una aproximación cercana a la deseada y solamente ajustando las pequeñas variantes de
cada control, la implementación fue hecha mediante el control Proporcional - Integrativo
para los tres casos. A continuación se explican los bloques de control y secuencia lógica
que fueron necesarios incorporar al sistema, para verificar el funcionamiento de la UTG.
A.3 Modelo del Sistema UTG
La figura A.2 muestra el sistema completo del la UTG en ambiente simulink. El
sistema completo esta formado por cuatro bloques que forman a todo el sistema Turbogás,
los cuales son; el bloque de control, de secuencia lógica, adquisición de datos (necesario
para interpretar el muestreo de las señales de la UTG) y el bloque de la Unidad Turbogás.
79
ANEXO A
AMBIENTE DE PRUEBA
Figura. A.2 Diagrama a Bloques del Sistema UTG
A.3.1 Bloque de control
En el primer bloque de la figura anterior (fig. A.3), se encuentran los controles que
mantienen a la turbina en condiciones estables, y cercanos a los valores de referencia
previamente establecidos. En la primera posición se encuentra el Control de Potencia que es
aquel que mantiene el valor de potencia generada, teniendo en cuenta que la operación de
éste control comienza una vez que la turbina llegó al valor de velocidad de sincronismo. En
segunda posición se encuentra el control de velocidad, donde su mayor participación la
tiene cuando la UTG está en la condición de arranque, y posteriormente mantendrá al
sistema a la velocidad de sincronismo (constante). Como tercer y último sub-bloque se
encuentra el control de temperatura de los gases de escape de la turbina, que toma un valor
muy importante para asegurar la utilización de la UTG, y de esta forma confiar de un largo
período de vida. Todos ellos son sumamente importantes para el desempeño de la unidad
turbogás (fig. A.3).
Figura. A.3. Etapa de control de la UTG.
80
ANEXO A
AMBIENTE DE PRUEBA
A.3.2 Bloque del secuenciador
En el segundo Bloque del Diagrama principal de la figura A.2 se tiene la secuencia
lógica, este bloque es el encargado de llevar a cabo los pasos necesarios para el arranque de
la turbina. Es aquí donde se establecen las etapas y permisivos para llevar a la unidad desde
la velocidad cero hasta la velocidad de sincronismo (figura. A.4).
La operación del bloque de la fig. A.4 de la secuencia lógica es la siguiente; La
entrada uno corresponde a la velocidad angular de giro del sistema compresor-turbina que
es acelerada por el motor de arranque y es detectada en los cuatro sub-bloques de esta etapa
secuencia lógica, donde en el primer sub-bloque se detectada la velocidad Kmotor_ar, que
indica la velocidad máxima a la cual el motor de arranque debe desacoplarse del sistema,
mandando como señal un “uno lógico” a la variable 4cr que indica un paro en el motor de
arranque. En el segundo sub-bloque las instrucciones son detectar el valor de la constante
Ksang, que indica el valor máximo que debe tomar la velocidad para que las válvulas de
sangrado se cierren y los álabes guía se abran, otorgando las literales SC_AG (señal de
control Alabes guía) en un “cero lógico” y SC_VS (señal de control de válvulas de
sangrado) en un “uno lógico”. En el tercer sub-bloque se realizan las siguientes tareas, las
cuales son; detección de la velocidad Kenc_q, que indica encendido de los combustores
para preparación de la UTG, al tiempo que se detecta la presencia de flama en los
combustores y se inicia el período de precalentamiento por 60 seg., una vez terminado el
período de calentamiento se genera la rampa de referencia para la velocidad de la turbina.
Fig A.4. Diagrama que muestra la parte del secuenciador lógica de la UTG.
81
ANEXO A
AMBIENTE DE PRUEBA
A.3.3 Bloque de la unidad turbogas
A continuación se muestra el tercer bloque de la Unidad Turbogás en Simulink la
imagen (figura. A.5), muestra el interior de la UTG donde se aprecia la interconexión del
Compresor - Cámara de Combustión – Turbina, juntamente con las válvulas de
combustible, de sangrado y la de los alabes guía.
Como anteriormente se explicó su funcionamiento inicia con la introducción de aire
al compresor, en donde éste lo comprime y lo envía a la cámara de combustión y los gases
calientes producto de la combustión pasan a través de la turbina donde se expanden y hacen
girar a la turbina, obteniéndose energía mecánica útil para hacer girar al generador
eléctrico. Ésta es la operación que realiza el modelo, además de contemplar detalladamente
la secuencia de arranque para tener el desarrollo eficiente para reproducir la dinámica de la
Unidad Turbogás.
Figura. A.5 Diagrama interno de la UTG, válvulas de combustible, sangrado y álabes guía, Compresor, Cámara de
Combustión y Turbina.
Como anteriormente se explicó su funcionamiento inicia con la introducción de aire
al compresor, en donde éste lo comprime y lo envía a la cámara de combustión y los gases
calientes producto de la combustión pasan a través de la turbina donde se expanden y hacen
girar a la turbina, obteniéndose energía mecánica útil para hacer girar al generador
eléctrico. Ésta es la operación que realiza el modelo, además de contemplar detalladamente
la secuencia de arranque para tener el desarrollo eficiente para reproducir la dinámica de la
Unidad Turbogás.
82
ANEXO A
AMBIENTE DE PRUEBA
La dinámica de la secuencia de arranque controla las cuatro válvulas mostradas en
la figura anterior, las cuales son las siguientes:
•
•
•
Válvula de Control y Corte de combustible.
Válvula de Sangrado.
Válvula de Álabes Guía.
Válvula de Control y Corte de combustible. Éstas válvulas de control permiten
regular el flujo de combustible a la cámara de combustión. La válvula de corte interrumpe
el flujo de combustible en caso de un paro normal o de emergencia de la unidad.
Válvula de Sangrado. Mediante ésta válvula se tiene una descarga de aire que sale
a la atmósfera en el arranque, esto para evitar inestabilidad en el sistema, y una vez
llegando al 95% de la velocidad nominal (5100 rpm), se cierra ésta válvula para darle
mayor desempeño.
Válvula de Alabes Guía. Mediante esta válvula se tiene control sobre los álabes
guía, en donde al inicio su posición es de aproximadamente el 50%, y cuando la velocidad
llega a un 95%, éstos se abren a un 75% para darle mayor flujo de aire a la Turbina.
A.4 Pruebas de Simulación de la UTG.
Teniendo en cuenta todas las consideraciones que en los apartados anteriores se han
mencionado, se muestra en esta sección la simulación de la UTG. Primero se parte de dar
de alta las condiciones iniciales de todas las variables del proceso que lo requieran. Para la
condición en que la turbina tiene un comienzo de Arranque en Frío, es decir, que la
Turbogás comienza desde velocidad cero, se inicializan las variables del proceso con el
programa denominado “Val_pro1_5.m” donde están todos los parámetros establecidos
bajo esa condición de Simulación.
Retomando nuevamente la figura A.2 se ve en la parte inferior izquierda tres
botones de condiciones; El primero es para dar de alta las condiciones iniciales en las que el
programa iniciará, y lo constituyen tres archivos. El inicial da instrucciones de borra del
espacio de trabajo y de todas las variables que en él existan (dejando limpio de basura),
para dar a inicio una simulación, otro archivo indica la utilización de todas las variables en
la Unidad Turbogás, y el último indica el estado en que operará la turbina, donde las
opciones son; de Arranque en Frío, Carga Base o de Sincronismo. El segundo botón es para
poner en “uno lógico” la variable de inicio del Motor de Arranque y El tercero muestra
ayuda general del comienzo de una nueva simulación.
Al oprimir los dos primeros botones del programa, el sistema de simulación queda
listo para entrar en funcionamiento
Terminado el tiempo de simulación, en el interior de cada bloque existen
osciloscopios que registran el comportamiento de las variables, así como también hay
bloques que almacenan los datos de algunas variables específicas para un posterior análisis
83
ANEXO A
AMBIENTE DE PRUEBA
detallado. En la figura A.6 se observan las variables principales y más importantes de la
unidad turbogás como son la velocidad angular, la potencia generada y la temperatura de
los gases de escape. Obteniéndose de manera visual la dinámica de la turbina de gas (todo a
partir del modelo matemático de la misma).
Figura A.6 Gráfica de las respuestas de la UTG
84
ANEXO B
ANFISEDIT
ANFISEDIT
B.1 Introducción.
Esta herramienta de Matlab aplica técnicas de inferencia difusa para el modelado de
datos, prácticamente cubre la secuencia de pasos del procedimiento básico de diseño visto
anteriormente.
El editor gráfico esta subdividido en 4 submenus principales, mediante los cuales se
realiza el diseño y el entrenamiento del sistema neurodifuso. En este anexo se presentan los
pasos que se llevaron a cabo para generar el sistema neurodifuso que representará el control
neurodifuso multivariable.
85
ANEXO B
ANFISEDIT
B.2 Procedimiento de diseño
Paso 1 Cargar Datos
En esta primera parte se carga la matriz de datos generada anteriormente, la cual
contiene los datos normalizados de entrenamiento obtenidos del modelo de la unidad
turbogas, estos mismos datos serán los que se utilizan para la validación del sistema
neurodifuso, no se emplean otro grupo diferente de datos para validación, ya que se
considera que el primer grupo fue recolectado sin ruido en la medición.
La figura B.1 muestra la ventana gráfica del editor de ANFIS, desplegando la
gráfica de los datos de entrenamiento, los cuales aparecen como un conjunto de círculos. El
eje horizontal es llamado data set index. Este índice indica la fila de la cual los valores de
los datos de entrada fueron obtenidos (cada fila contienen un dato de velocidad, potencia y
temperatura) y el eje vertical los valores de la salida (señal de control) para cada fila.
En la parte superior derecha de la figura B.1 se muestra el número de entradas, el
número de salidas, número de funciones de membresía (aun no se definen) y del número de
patrones de entrenamiento cargados.
Figura. B.1 Datos de entrenamiento
Paso 2 Inicialización y generación del sistema de inferencia difuso.
El sistema de inferencia difuso se puede inicializar de dos formas, estas pueden ser
de acuerdo a la experiencia, conocimiento del proceso y preferencias de cómo se quiere
iniciar los parámetros de las funciones de membresía o dejar que el editor de ANFIS
86
ANEXO B
ANFISEDIT
automáticamente realice estas tareas. Esta segunda opción es una de las grandes ventajas
de utilizar el editor ANFIS ya que se logran los mismos resultados con menor esfuerzo.
Para la realización de este trabajo se eligió la segunda opción, para la inicialización
del sistema difuso usando la inicialización automática de ANFIS se siguen los siguientes
pasos:
1.
Escoger el método de partición del sistema difuso, en este caso se selecciona el
método Grid partition, es el método de particionamiento por default de ANFIS
(segundo submenu de la figura B.4).
2.
Oprimir el botón de Generate FIS (Generar sistema de inferencia difuso) el cual
desplegará el submenú que se muestra en la figura B.2 en el cual se escogen el número
de funciones de membresía, el tipo de funciones de membresía de entrada y salida.
Como ANFIS sólo maneja sistemas de inferencia tipo Sugeno sólo tiene dos tipos de
funciones de membresía de salida: constante y lineal. Para éste caso se definieron 3
funciones de membresía para cada entrada del tipo trapezoidal y la salida como una
combinación lineal.
Figura. B.2 Selección de numero y tipo de funciones de membresía.
El índice de error que genera el entrenamiento del sistema neurodifuso, depende de
la selección del tipo y número de funciones de membresía, para el caso del sistema
neurodifuso que se está entrenando, entre más funciones de membresía sean consideradas,
menor será este índice de error, pero el esfuerzo de entrenamiento es mayor llegando en la
mayoría de las ocasiones a entrenamientos inconclusos debido a limitaciones impuestas por
el hardware ya que el número de parámetros de la red aumenta exponencialmente.
87
ANEXO B
ANFISEDIT
Paso 3 Entrenamiento ANFIS
Hay 2 métodos de optimización disponibles para el entrenamiento del sistema de
inferencia difuso, estos son: el método híbrido (es el método por default, mezcla
backpropagation y mínimos cuadrados) y el método backpropagation. El error de tolerancia
es usado para crear un criterio para detener el entrenamiento, este está relacionado con el
tamaño del error, cuando este alcanza la tolerancia el entrenamiento finaliza. El error es la
diferencia entre los valores de salida de los datos de entrenamiento y las salidas del sistema
de inferencia difuso correspondiente a los mismos datos de entrenamiento de entrada Otro
criterio para detener el entrenamiento es definiendo el numero de épocas para el
entrenamiento.
En este caso se seleccionó el método de aprendizaje híbrido, debido a que es más
rápido por combinar el algoritmo de aprendizaje de gradiente descendente y el de mínimos
cuadrados, el método backpropagation afecta los parámetros asociados con las funciones de
membresía de entrada y el método de mínimos cuadrados afecta los parámetros asociados
con las funciones de membresía de salida, se tomó el valor por default el error que es cero
y se definieron 30 épocas de entrenamiento.
En la figura B.3 se observa el comportamiento del error durante las 30 épocas de
entrenamiento, el error va decrementando paulatinamente hasta alcanzar su valor mínimo.
Figura B.3 Comportamiento del error durante el entrenamiento
PASO 4 Prueba del sistema de inferencia difuso entrenado.
Después de haber terminado el entrenamiento, se procede a verificarlo contra los
mismos datos, si la verificación es satisfactoria, como se observa en la figura B.4 se
88
ANEXO B
ANFISEDIT
procede a guardar el sistema neurodifuso generado en un archivo con formato “.fis” para
después poder incorporarlo como un bloque funcional al modelo del sistema en Simulink.
Figura B.4 Verificación del entrenamiento del sistema neurodifuso
ANFIS es un sistema difuso complejo y sólo soporta sistemas difusos tipo Sugeno y
estos deben cumplir las siguientes propiedades.
•
Ser un sistema difuso de tipo Sugeno.
•
Tener una sóla salida, obtenida usando la defusificacion por promedio de los pesos
de todas las salidas.
•
No hay reglas compartidas, diferentes reglas no pueden compartir la misma función
de membresía de salida, es decir el número de funciones de membresía de salida debe
ser igual al numero de reglas.
•
Tener pesos unitarios para cada regla.
Por lo anterior ANFIS no acepta todas las opciones que los sistemas de inferencia básicos
permiten.
89
ANEXO C
Fundamentos de lógica difusa, redes neuronales, sistemas neurodifusos y ANFIS
Fundamentos de lógica difusa, redes
neuronales, sistemas neurodifusos y
ANFIS
C.1 Lógica difusa
La lógica difusa (LD)ha cobrado una gran fama por la variedad de sus aplicaciones,
las cuales van desde el control de complejos procesos industriales, hasta el diseño de
dispositivos artificiales de deducción automática, pasando por la construcción de artefactos
electrónicos de uso doméstico y de entretenimiento, así como también de sistemas de
diagnóstico. La expedición de patentes industriales de mecanismos basados en la lógica
difusa tiene un crecimiento sumamente rápido en todas las naciones industrializadas del
orbe.
La lógica difusa trata de crear aproximaciones matemáticas en la resolución de
ciertos tipos de problemas. Pretenden producir resultados exactos a partir de datos
imprecisos, por lo cual son particularmente útiles en aplicaciones electrónicas o
computacionales.
El adjetivo ``difuso'' aplicado a esta lógica se debe a que en ella los valores de
verdad no-deterministas utilizados tienen, por lo general, una connotación de
incertidumbre. Un vaso medio lleno, independientemente de que también esté medio vacío,
no está lleno completamente ni está vacío completamente. Qué tan lleno puede estar es un
elemento de incertidumbre, es decir, de difusidad, entendida esta última como una
propiedad de indeterminismo. Ahora bien, los valores de verdad asumidos por enunciados
aunque no son deterministas, no necesariamente son desconocidos. Por otra parte, desde un
punto de vista optimista, lo difuso puede entenderse como la posibilidad de asignar más
90
ANEXO C
Fundamentos de lógica difusa, redes neuronales, sistemas neurodifusos y ANFIS
valores de verdad a los enunciados que los clásicos ``falso'' o ``verdadero''.
Consecuentemente, la lógica difusas es un tipo especial de lógica multivaluada.
Conjuntos difusos
El concepto más fundamental en teoría de lógica difusa es el concepto de conjunto difuso
(CD). Un CD en un universo de discurso U es caracterizado por una función de
pertenencia A(x) que toma valores en el intervalo [0,1]. De esta manera, un CD es una
generalización de un conjunto clásico permitiendo que su función de pertenencia (FP) tome
valores en el intervalo [0,1]. Es decir, una FP de un conjunto clásico puede solamente tomar
dos valores: cero o uno, mientras que una FP de un CD es una función continua con rango
[0,1]. [29].
De esta manera, un CD A en U puede ser representado como un conjunto de pares
ordenados de un elemento genérico x y su valor de pertenencia, esto es:
A = {(x, µA(x)) | x ∈ U}
Donde U es continuo.
El CD A es comúnmente escrito como:
µ A ( x ) / x,
A=
si U es discreto.
U
µ A ( x ) / x,
si U es continuo.
U
Los signos de sumatoria e integración no representan suma aritmética ni integración
sino la colección de todos los puntos x ∈ U asociados con la FP µA(x). Similarmente, “/” es
solamente una marca y no implica división.
La figura A1 muestra las FP’s de tres CD llamados “Lento”, “Moderado” y
“Rápido” para la velocidad de un carro. El universo de discurso es el rango de velocidad
que puede tener un automóvil, esto es, U= [0, Vmax], donde Vmax es la máxima velocidad del
automóvil.
µ A( VMax)
0
Lento
Moderado
Rápido
V Max mph
75
55
Figura C.1 Funciones de pertenencia de tres conjuntos difusos para la velocidad de un automóvil
35
91
ANEXO C
Fundamentos de lógica difusa, redes neuronales, sistemas neurodifusos y ANFIS
Existe una gran variedad de FP’s, y se necesita un planteamiento para su elección.
Conceptualmente hay dos planteamientos para determinar una FP:
1. El primero utiliza el conocimiento de los humanos expertos, es decir, se
apoya en el dominio de los expertos para especificar las FP’s. Las FP’s
representan parte del conocimiento humano, por ello los CD’s son
frecuentemente usados para formular el conocimiento humano.
2. El segundo planteamiento, se utilizan datos reunidos desde varios sensores
para determinar las FP’s. Específicamente, primero se especifican las
estructuras de las funciones de membresía y luego se sintonizan finamente
los parámetros de las funciones de pertenencia basados en los datos.
Operaciones básicas de conjuntos difusos
Sea A y B dos CD’s definidos en el mismo universo de discurso U, con FP’s µA(x) y
µB(x), respectivamente. Las operaciones teóricas de conjuntos de unión, intersección y
complemento para CD’s se definen a continuación.
Unión [Norma-S]
La FP µA∪B de la unión A∪B de los conjuntos A y B se define para toda x ∈ U por:
µA∪B(x)= max{µA(x), µB(x)}.
Intersección [Norma-T]
La FP µA∩B de la unión A∩B de los conjuntos A y B se define para toda x ∈ U por:
µA∩B(x)= min{µA(x), µB(x)}.
Con frecuencia, los operadores de unión y de intersección son denotados por ∨ y ∧,
respectivamente.
Complemento
La FP µ A del complemento de un CD A se define para toda x ∈ U por:
µ A (x)= 1 - µA(x).
Producto Cartesiano
Si A1, A2, ,,,, An son conjuntos difusos en U1,U2, ,,,, Un respectivamente, el
producto cartesiano de A1,A2,..., An es un conjunto difuso en el espacio producto U1 X U2 X
... X Un con la función de pertenencia:
µ A1X A2 X ,,,,X An(u1, u2, ..., un) = min[µ A1(u1), µA2(u2), ..., µAn (un)]
92
ANEXO C
Fundamentos de lógica difusa, redes neuronales, sistemas neurodifusos y ANFIS
o
µ A1X A2 X ,,,, X An(u1, u2, ..., un) = µ A1(u1) ⋅ µA2(u2) ⋅ ... ⋅ µAn (un)
Variables lingüísticas y conjuntos difusos
En nuestra vida diaria, las palabras son a menudo usadas para describir variables.
Por ejemplo, cuando decimos “hoy hace calor”, o equivalentemente, “hoy la temperatura es
alta”, utilizamos la palabra “alta” para describir la variable “hoy la temperatura.” Por
consiguiente, la variable “hoy la temperatura” toma la palabra “alta” como su valor. Es
claro que la variable “hoy la temperatura” también puede tomar números como 25°C, 19°C,
etc., como sus valores. Cuando una variable toma números como sus valores, tenemos bien
establecida una estructura para formular ésta. Pero cuando la variable toma palabras como
sus valores, no tenemos una estructura formal para formular ésta en teoría matemática
clásica. En orden de proporcionar esa estructura formal, el concepto de variable lingüística
(VL) fue introducido. Así, para formular palabras en términos matemáticos se usan CD’s
para caracterizar estas palabras.
Definición de Variable Lingüística
Si una variable puede tomar palabras en un lenguaje natural como sus valores, ésta
es llamada VL, donde las palabras son caracterizadas por CD definidos en el universo de
discurso en el cual la variable es definida.
En la figura C.1 se definieron tres CD llamados “Lento”, “Moderado” y “Rápido” en [0,
Vmax]. Si se mira x como una VL, entonces ésta puede tomar como sus valores “Lento”,
“Moderado” y “Rápido”, así, se puede decir “x es Lento”, “x es Moderado” y “x es
Rápido”. Por supuesto x también puede tomar números en el intervalo [0, Vmax] como sus
valores, por ejemplo, x = 50 mph, 35 mph, etc.
Estas dos definiciones son esencialmente equivalentes y desde las cuales se puede
ver que una VL es una extensión de una variable numérica en el sentido que permiten tomar
CD’s como sus valores.
El concepto de VL es muy importante porque las VL’s son los elementos más
fundamentales en la representación del conocimiento humano. Cuando se utilizan sensores
para medir una variable, estos nos dan números; cuando se le hacen preguntas a los
expertos humanos para evaluar una variable, ellos proporcionan palabras. Al introducir el
concepto de VL, se es capaz de formular descripciones vagas en un lenguaje natural en
términos matemáticos precisos. Este es el primer paso para incorporar el conocimiento
humano dentro de sistemas de ingeniería en una manera sistemática y eficiente.
Razonamiento a Aproximado
En la lógica tradicional existen dos reglas de inferencia, el Modus Ponens y Modus
Tollens:
93
ANEXO C
Fundamentos de lógica difusa, redes neuronales, sistemas neurodifusos y ANFIS
Modus Ponens:
Premisa 1 (antecedente): si x es A entonces y es B
Premisa 2 (antecedente): x es A;
Consecuencia: y es B.
Modus Tollens:
Premisa 1: si x es A entonces y es B
Premisa 2: y es B
Consecuencia: x es A.
Ejemplo de Modus Ponens Generalizado:
Premisa 1: si nivel es bajo entonces abrir válvula,
Premisa 2: nivel es poco bajo,
Consecuencia: abrir poco la válvula.
Funciones de pertenencia
Las opciones mas populares de las figuras en las FP´s son las funciones triangular,
trapezoidal y campana. Estas tres opciones definidas por la facilidad de sus parámetros,
descripción funcional de las FP´s, almacenadas con un mínimo uso de memoria y
manipuladas eficientemente por la máquina de inferencia.
La FP triangular debido a sus parámetros y descripción funcional es la más económica.
Esto explica su predominante uso en este tipo de FP.
Tabla C.1 Funciones de pertenencia
Función
Fórmula Analítica
(x )
Triangul
ar A
Representación Gráfica
µ A (x )
A (x; a , b , c ) = max 0, min
µ A( x)
x−a c−x
,
b−a c−b
Parámetros : a , b, c
(x )
A
0
a
µ B( x)
µ B (x )
x
c
b
B
Trapecio
x−a d −x
B (x; a, b, c, d , ) = max min
,1,
,0
B
b−a d −c
a<b<c<d
Parámetros : a, b, c y d
0
94
a
b
c
d
x
ANEXO C
Fundamentos de lógica difusa, redes neuronales, sistemas neurodifusos y ANFIS
(x )
µ C (x )
C ( x; a , b , c ) =
Campana
C
µC( x)
1
x−c
1+
a
2b
C
,b>0
a
b
Parámetros : a, b y c
0
c
Sistemas de inferencia difusos
Un sistema de inferencia difuso emplea reglas si-entonces las cuales pueden
modelar aspectos cualitativos de procesos, de razonamiento y de conocimiento humano sin
emplear un análisis cuantitativo preciso. Este modelado difuso o identificación difusa fue
explorada sistemáticamente por Takagi y Sugeno [30], encontrando numerosas aplicaciones
prácticas en control [31,32], predicción e inferencia [33,34]. Sin embargo hay 2
restricciones básicas acerca de los sistemas de inferencia difusos los cuales deben ser
comprendidos, estos son:
•
•
No existen métodos estándar para transformar la experiencia o conocimiento
humano en base de datos y base de reglas de un sistema de inferencia difuso.
Hay una necesidad de métodos efectivos que nos permitan sintonizar las funciones
de membresía, así como minimizar el error de salida o maximizar el índice de
desempeño.
ANFIS puede servir como una base para construir un conjunto de reglas de
inferencia difusas si-entonces con funciones de membresía apropiadas para generar los
pares de entrada-salida estipulados.
Reglas difusas si entonces
Las reglas difusas si-entonces o las declaraciones condicionales difusas son
expresiones de la forma:
IF A THEN B
(Si A entonces B)
Donde A y B son valores lingüísticos de conjuntos difusos, caracterizados por
funciones de membresía apropiados [35]. Debido a su forma concisa, las reglas difusas sientonces frecuentemente se emplean para capturar las formas imprecisas de razonamiento
que juegan un papel esencial en la habilidad humana para tomar decisiones en un ambiente
de imprecisión e incertidumbre. Un ejemplo que describe un simple hecho es:
Si la presión es alta, entonces el volumen es pequeño.
Donde presión y volumen son variables lingüísticas [36], alto y pequeño son valores
lingüísticos los cuales son caracterizados por funciones de membresía.
95
x
ANEXO C
Fundamentos de lógica difusa, redes neuronales, sistemas neurodifusos y ANFIS
Otra forma de reglas de inferencia difusas si – entonces, propuestos por Takagi y
Sugeno [37] involucran conjuntos difusos sólo en la parte de los antecedentes, por ejemplo:
Si la velocidad es alta, entonces fuerza = k * (velocidad)²
Donde, nuevamente en la parte del antecedente alta es un valor lingüístico
caracterizado por una función de membresía apropiada, sin embargo, la parte consecuente
es descrita por una ecuación que no es difusa, involucrando a la variable de entrada
(velocidad).
Ambos tipos de reglas difusas han sido usadas ampliamente tanto en control como
modelado, una regla difusa si – entonces fácilmente puede capturar la esencia de una regla
de dedo humana por medio de funciones de membresía y variables lingüísticas. Las reglas
difusas si – entonces forman la parte central del sistema de inferencia difuso.
Sistemas de Inferencia Difusos.
Los sistemas de inferencia difusos también son conocidos como sistemas basados en
reglas difusas, modelos difusos, memorias asociativas difusas o controladores difusos,
cuando son utilizados como controladores. Básicamente un sistema de inferencia difuso
está compuesto por 5 bloques funcionales (fig. 4.3) estos son:
Base de reglas. Contiene un número de reglas de inferencia difusas.
Base de Datos. Define las funciones de membresía de los conjuntos difusos usados
en las reglas difusas.
Máquina de inferencia. Realiza las operaciones de inferencia con las reglas.
Interface de fusificación. Esta es la interface entre la máquina de inferencia y el
proceso. El módulo de fusificación permite calcular un valor que representa el grado de
pertenencia o membresía de una medición de variables de estado del proceso en uno o más
conjuntos difusos especificados en el universo de discurso. En otras palabras es donde el
valor real (numérico) se convierte a un valor difuso (lingüístico).
Interface de defusificación. La salida final de la máquina de inferencia difusa es un
conjunto difuso, pero ya que la mayoría de los sistemas requieren que la salida sea una
variable de valor real, se necesita de una interfase de defusificación para convertir el
conjunto difuso en un valor numérico. En otras palabras, el proceso de defusificación
determina una acción de control actual desde un conjunto difuso producto de acciones de
control inferidas desde las reglas difusas. En la literatura existen varios métodos de
defusificación.
Usualmente las bases de reglas y bases de datos son nombradas conjuntamente
como base de conocimiento (figura C.2.).
96
ANEXO C
Fundamentos de lógica difusa, redes neuronales, sistemas neurodifusos y ANFIS
Base de
Conocimiento
Base
Base
de
de
Datos Reglas
x en U
Fusificación
Conjuntos
difusos en U
Defusificación
Maquina de
Inferencia
y en V
Conjuntos
difusos en V
Figura.C.2 Bloques funcionales del sistema difuso
Los pasos básicos del razonamiento difuso (operaciones de inferencia en reglas de
inferencia Si – Entonces) realizados por sistemas de inferencia difuso son:
1. Comparar las variables de entrada con las funciones de membresía en la parte de los
antecedentes para obtener los valores de membresía (grados de membresía o
medidas de compatibilidad) de cada variable lingüística (este paso frecuentemente
es conocido como fusificación).
2. Combinar (a través de un operador especifico Norma-T, usualmente multiplicación
o mínimo) los valores de membresía de los antecedentes para obtener la fuerza de
disparo (peso) de cada regla.
3. Generar los consecuentes correctos (ya sea difusos o numéricos) de cada regla
dependiendo de la fuerza de disparo.
4. Agregar los consecuentes calculados para producir una salida numérica. (Este paso
es llamado defusificación).
En la literatura dependiendo del tipo de razonamiento difuso y del tipo de reglas si –
entonces empleadas, la mayoría de los sistemas difusos pueden ser clasificados en tres
tipos (figura C.3):
Tipo 1: La salida global es el promedio de la fuerza de disparo de cada regla por las
funciones de membresía de salida.
Tipo 2: La salida global difusa es calculada con la aplicación de la operación “max”de
las salidas difusas competentes (cada una de las cuales es igual al mínimo de la fuerza de
disparo y la función de membresía de salida de cada regla). Varios esquemas han sido
propuestos para proporcionar la salida numérica final basada en todas las salidas difusas;
algunos de ellos son el centro del área, bisector del área, criterio máximo, etc [25,26].
97
ANEXO C
Fundamentos de lógica difusa, redes neuronales, sistemas neurodifusos y ANFIS
Tipo 3: Takagi y Sugeno, usan reglas difusas Si – Entonces, la salida de cada regla
es una combinación lineal de las variables de entrada más un término constante, y la
salida final es el promedio ponderado de la salida de cada regla.
tipo 1
A3
A1
tipo 2
tipo 3
C3
C1
f1 = p1 x + q1 y + r1
w1
a1 b1
c1
X
A2
a3 b3
c3
f1
Y
A4
f
f
C2
f 2 = p2 x + q2 y + r2
C4
w2
a2 b2
x
c2
X
a4 b4
c4
Y
y
a2 b2
c2
f2
f
f
multiplicación
( o min)
f =
w1 f1 + w2 f 2
w1 + w2
centroide del area
f
f =
w1 f1 + w2 f 2
w1 + w2
= w1 f1 + w2 f 2
Figura C.3 Tipos de razonamiento difuso
C.2 Fundamentos de Redes Neuronales
Las Redes Neuronales (RN) aparecen como una poderosa técnica de reconocimiento
de patrones, las cuales surgen en el momento en que las computadoras interactúan con el
mundo real. Las redes neuronales son ampliamente usadas en muchas aplicaciones. La
evaluación de la aplicación de las redes neuronales requieren de un conocimiento previo de
los algoritmos necesarios y técnicas desarrolladas, así como de sus fuerzas y debilidades.
Como otras técnicas de reconocimiento de patrones, las redes neuronales actúan sobre datos
detectando algunos tipos de organización fundamentales. Las RN pueden realizar tareas de
clasificación, predicción y estimación[40].
Las RN aprenden similitudes entre patrones de datos, infieren soluciones desde los
datos sin conocimiento previo de ellos, extrayendo las similitudes empíricamente.
Este es un aspecto distintivo en muchas aplicaciones ya que no trabajan como la
programación convencional. Mientras más se conozca el problema mejor es el diseño. Las
RN son entrenadas y no programadas lo que las diferencia del software.
98
ANEXO C
Fundamentos de lógica difusa, redes neuronales, sistemas neurodifusos y ANFIS
Pueden generalizar, es decir, responder correctamente a patrones que son solo
similares a los patrones de entrenamiento original. La generalización es útil ya que los
datos del mundo real son ruidosos, distorsionados y a menudo incompletos. Las RN son no
lineales, es decir, pueden resolver algunos problemas complejos mejor de lo que lo hacen
las técnicas lineales. El comportamiento no lineal es común pero matemáticamente difícil
de manejar.
Como característica importante, las RN son altamente paralelas. Contienen muchas
operaciones que son idénticas e
independientes que pueden ser ejecutadas
simultáneamente. Esto es útil ya que el hardware paralelo puede correr RN muy rápido,
haciéndolo en ocasiones más rápido que los métodos alternativos. Las RN pueden aprender
algunas cosas diferentes para las cuales fueron entrenadas.
Básicamente la estructura de una red neuronal esta formada por nodos (de entrada,
salida y ocultos), conexiones capas y pesos que son prácticamente universales pero los
arreglos entre ellos varían.
Las RN imitan funciones, y esta es la base para medir su desempeño, a esta
habilidad se le conoce con el nombre de función de estimación, modelado o aproximación,
y se aplican en muchos aspectos como clasificación, predicción, patrones de
reconocimiento y agrupaciones. Los programas de computadoras pueden hacer tareas
similares, sin embargo algunas de estas tareas serán simples para un método, mientras para
el otro apenas serán posible.
Los programas de computadoras son buenos en aplicaciones donde se requieren
gran exactitud en cálculos numéricos y manipulación de símbolos, para una RN esta tarea
probablemente sea muy difícil de aprender. Las RN, muestran un mejor desempeño en
aplicaciones donde existen pocas reglas obvias, se trata con datos imperfectos, y se tienen
que optimizar muchas restricciones simultáneamente. Las redes neuronales raravez son
aplicaciones aisladas, generalmente forman parte de una gran aplicación.
Ventajas de las RN.
•
•
•
•
Se pueden utilizar para estimación de funciones.
Pueden entrenarse con datos imprecisos.
Habilidad para tolerar resultados aproximados o complejos.
Comportamiento no lineal.
Desventajas de la RN.
•
•
•
Pueden fallar en la búsqueda de la solución correcta, quizás a una función
inaprendible o a datos insuficientes.
Los resultados de una RN son difíciles de explicar.
Las RN pueden ser lentas y caras de entrenar.
99
ANEXO C
•
Fundamentos de lógica difusa, redes neuronales, sistemas neurodifusos y ANFIS
El tiempo de ejecución depende del numero de conexiones, las cuales son
típicamente el cuadrado de los nodos, incrementos pequeños en el numero de nodos
causa grandes incrementos en el tiempo de ejecución.
Redes neuronales artificiales.
El concepto de Red Neuronal Artificial (RNA) está inspirado en las Redes
Neuronales Biológicas. Una Red Neuronal Biológica es un dispositivo no lineal altamente
paralelo, caracterizado por su robustez y su tolerancia a fallos.
•
•
•
Sus principales características son las siguientes:
Aprendizaje mediante adaptación de sus pesos sinápticos de acuerdo al entorno que
la rodea.
Manejo de imprecisión, ruido e información probabilística.
Generalización de salidas a partir de ejemplos.
Las Redes Neuronales Artificiales intentan imitar algunas, o todas, de estas
características. Este paradigma de programación difiere de las secuencias de instrucciones
en que la información se encuentra almacenada en las conexiones sinápticas. Cada neurona
es un procesador elemental con operaciones muy primitivas como la suma ponderada de
sus pesos de entrada y la amplificación o umbralización de esta misma suma.
La Red Neuronal se caracterizada por su topología, por la intensidad de la conexión
entre sus pares de neuronas (pesos), por las propiedades de todos los nodos y por las reglas
de actualización de pesos. Las reglas de actualización, también llamadas de aprendizaje,
controlan los pesos y/o estados de los elementos del proceso (neuronas).
Los principales aspectos de este modelo de computación distribuida son los
siguientes:
•
•
•
•
•
Un conjunto de unidades de procesamiento.
Un estado de activación y k para cada unidad, que es equivalente a la salida de la
unidad.
w jk
Conexiones entre unidades, generalmente definidas por un peso
,que
determinan el efecto de la unidad j sobre la unidad k.
Una regla de propagación que determina la entrada de la unidad sk a partir de sus
entradas externas.
Una función de activación Fk que determina el estado de activación en función de
la entrada de la unidad (en algunos casos la función de activación tiene en cuenta la
activación actual de la unidad).
•
Una entrada externa (u offset) θ k para cada unidad.
•
Un método para modificar los valores de los pesos (regla de aprendizaje).
100
ANEXO C
•
Fundamentos de lógica difusa, redes neuronales, sistemas neurodifusos y ANFIS
Un entorno de trabajo en el que sistema opere, compuesto por señales de entrada y,
si es necesario, señales de error.
Modelo de la neurona
A los elementos individuales de cálculo que forman los modelos de sistemas
neuronales artificiales reciben el nombre de Elementos de Procesamiento o Neuronas
Artificiales (nodo). Cada unidad realiza un trabajo muy simple: recibe impulsos de otras
unidades o de estímulos externos y calcula una señal de salida que propaga a otras unidades
y, además, realiza un ajuste de sus pesos. Este tipo de modelos es inherentemente paralelo
en el sentido de que varias unidades pueden realizar sus cálculos al mismo tiempo. El
elemento de procesamiento más simple suele tener el siguiente esquema, (figura C.4).
Neurona
x1
Entradas
x2
..
..
..
..
xn
w1
w2
wn
Fk
sk
yk
Salida
Pesos
θk Umbra
l
Figura C.4 Diagrama de la Red Neuronal
Artificial.
Este esquema de elemento de procesamiento tiene las siguientes características:
•
•
•
•
•
•
Cada elemento de proceso puede tener varias entradas asociadas a propiedades
diferentes.
La entrada de tendencia es opcional (valor constante).
Las entradas pueden ser: Excitadoras, inhibidoras, de ganancia, de disparo fortuito o
de amortiguamiento.
Las entradas están ponderadas por un factor multiplicativo de peso o intensidad de
conexión que resaltan de forma diferente la importancia de cada entrada..
Cada elemento de procesado tiene un valor de activación calculado en función del
valor de entrada neto (calculado a partir de las entradas y los pesos asociados a
ellas). En algunos casos, el valor de activación, depende además de la entrada neta
del valor anterior de activación.
Una vez calculado el valor de activación, se determina un valor de salida aplicando
una función de salida sobre la activación del elemento de procesamiento.
101
ANEXO C
Fundamentos de lógica difusa, redes neuronales, sistemas neurodifusos y ANFIS
Conexión entre neuronas.
En la mayor parte de los casos se asume que cada neurona recibe contribuciones
aditivas de las neuronas que están conectadas a ellas (enlaces). La entrada total de la unidad
k es la suma ponderada de las entradas que recibe, más el término de offset
sk =
j
w jk y j + θ k
Cuando el peso de la contribución es positivo se considera que la entrada es
“excitatoria” y cuando el peso es negativo que es “inhibidora”.
Funciones de activación y salida.
Además de la regla de propagación es necesario poseer expresiones para las
funciones de activación (son quienes calculan la activación, en función de la entrada total)
y funciones de salida (las que calculan la salida en función de la activación).
La función de activación calcula la activación de la neurona en función de la entrada
total y la activación previa, aunque en la mayor parte de los casos es simplemente una
función no decreciente de la entrada total. Los tipos de función más empleados son:
funciones con umbral lineal y la función sigmoide.
La función de salida empleada usualmente es la función identidad y así la salida del
proceso es idéntica a su nivel de activación.
Topología.
La topología es el número de elementos de proceso que forman la red y las
interconexiones existentes entre ellos. Los elementos de procesado de una red neuronal se
distribuyen por capas (conjunto de elementos de procesado que se encuentran en el mismo
nivel en la estructura).
Existen tres tipos de capas:
•
•
•
Capa de entrada: Dependen del problema a abordar.
Capa de salida: Salidas que proporciona la estructura.
Capas ocultas: conjunto de elementos de procesamiento asociados en capas que se
encuentran entre la capa de entrada y la capa de salida.
El número de elementos del proceso puede variar en unas capas respecto a las otras.
Las funciones (tanto de activación como de salida) de los elementos de procesamiento
pueden ser diferentes. No existe limitación en el número de capas ocultas. En general,
cuanto mayor sea la diferencia entre los elementos de entrada y los de salida, será necesario
dotar a la estructura de más capas ocultas. Estas capas ocultas crean una representación
interna de los patrones de entrada. La habilidad de la red para procesar información crece
en proporción directa al número de capas ocultas.
102
ANEXO C
Fundamentos de lógica difusa, redes neuronales, sistemas neurodifusos y ANFIS
Creación de un conjunto de datos.
Esta es la etapa mas larga y critica, en esta etapa se incluye la recopilación de datos,
su análisis, la selección de variables y el preprocesamiento de los datos (patrones de
entrada) con los cuales la red puede aprender eficientemente.
Las RN pueden reconocer nuevos ejemplos de patrones utilizados para entrenarlas,
pero solo si estos se asemejan al patrón original. El objetivo mayor es construir un índice
de series de patrones de entrada, cada uno de los cuales es un conjunto de los valores
medidos. Estas redes que aprenden de resultados conocidos también requieren de resultados
correctos para cada patrón de entrada. Los patrones de entrada son usualmente vistos como
un vector y los valores individuales como un vector de componentes.
En la practica la suficiencia de datos depende de varios factores: tamaño de la red,
pruebas necesarias y distribución de las entradas. El tamaño de la red toma mucha
importancia. Una red grande generalmente requiere de mas entrenamiento que una red
pequeña, por eso se debe tener cuidado en la selección de las variables de entrada y salida
para conservar pequeña la red, únicamente con los datos necesarios para entrenarla.
Configuración
El diseño de una red neuronal puede ser tan simple como seleccionar una red
comercial disponible, implementar el hardware o el sofware o la combinación de ambos y
configurarla de acuerdo con los datos. La selección del diseño de la red incluye definir el
comportamiento de los nodos, el procedimiento de entrenamiento, la topología de la red y
los valores de los parámetros de entrenamiento.
Después de seleccionar una red el siguiente paso es configurarla, ajustando el
numero de nodos de entrada y salida de acuerdo con el numero de datos de entradas y
salidas, algunas redes requieren valores adicionales los cuales deben ser asignados. Otras
redes permiten configurar otros aspectos como por ejemplo: cambiar el numero de capas
ocultas, la frecuencia de actualización de los pesos el tipo de función de transferencia y
otros factores.
Entrenamiento y pruebas.
Por ultimo la parte final del desarrollo es entrenar y probar la red, durante el
entrenamiento se hacen ciclos repetidamente a través de los datos cambiando los valores de
sus pesos para mejorar su desempeño. Cada paso a través del entrenamiento de datos es
conocido como una etapa, y la red aprende a través de la acumulación de los cambios
hechos a los pesos durante todas las etapas hasta que los pesos proporciona los resultados
mas adecuados.
Una red es usada solo si esta regresa resultados apropiados con datos que no han
sido usados para su entrenamiento, para la validación de esta habilidad llamada
generalización se requiere probar la red con un conjunto independiente de datos, durante
103
ANEXO C
Fundamentos de lógica difusa, redes neuronales, sistemas neurodifusos y ANFIS
estas pruebas la red calcula un índice de desempeño como puede ser el error cuadrático
promedio. Las pruebas durante el entrenamiento deben mostrar cuando termina este, para
evitar un sobreentrenamiento, también muestran cual configuración es mejor.
Apoyándonse en un índice de desempeño como puede ser el error cuadrático
promedio podemos evitar el sobreentrenamiento, parando el entrenamiento cuando el error
cuadrático promedio alcance su valor mas bajo.
El error cuadrático promedio de los conjuntos de pruebas y de entrenamientos en un
principio su valor va decayendo, y cuando el error cuadrático promedio del conjunto de
pruebas comienza a incrementarse, significa que la red a dejado de aprender y el
entrenamiento debe pararse.
Red backpropagation
El funcionamiento de la red backpropagartion (BP) consiste en el aprendizaje de un
conjunto predefinido de pares de entradas-salidas dados, como ejemplo: primero se aplica
un patrón de entrada como estímulo para la primera capa de las neuronas de la red, se va
propagando a través de todas las capas superiores hasta generar una salida, se compara el
resultado en las neuronas de salida con la salida que se desea obtener y se calcula un valor
de error para cada neurona de salida. A continuación, éstos errores se transmiten hacia
atrás, partiendo de la capa de salida hacia todas las neuronas de la capa intermedia que
contribuyan directamente a la salida, recibiendo de error aproximado a la neurona
intermedia a la salida original. Este proceso se repite, capa por capa, hasta que todas las
neuronas de la red hayan recibido un error que describa su aportación relativa al error total.
Basándose en el valor del error recibido, se reajustan los pesos de conexión de cada
neurona, de manera que en la siguiente vez que se presente el mismo patrón, la salida estará
más cercana a la deseada.
La importancia de la red backpropagation consiste en su capacidad de autoadaptar
los pesos de las neuronas de las capas intermedias para aprender la relación que existe entre
un conjunto de patrones de entrada y sus salidas correspondientes. Es importante la
capacidad de generalización, (facilidad de dar salidas satisfactorias a entradas que el
sistema no ha visto nunca en su fase de entrenamiento). La red debe encontrar una
representación interna que le permita generar las salidas deseadas cuando se le dan entradas
de entrenamiento, y que pueda aplicar, además, a entradas no presentadas durante la etapa
de aprendizaje para clasificarlas.
La clave del algoritmo de aprendizaje backpropagation consiste en su habilidad para
cambiar el valor de los pesos en función de los errores. Esto lo hace mediante un proceso
llamado gradiente descendente en el cual la red neuronal cambia los pesos de una forma
descenderte hasta el punto en el que se produzca el mínimo error ( promedio de la suma de
los errores cuadráticos).
104
ANEXO C
Fundamentos de lógica difusa, redes neuronales, sistemas neurodifusos y ANFIS
C.3 Sistemas Neurodifusos
El avance de los sistemas de Inteligencia Computacional y la búsqueda de
soluciones cada vez mas completas para los problemas, han llevado a la unión de técnicas
de programación, haciendo que las debilidades de unos sistemas se compensen con las
bondades de otros. De esta manera surge la unión de las técnicas de Redes Neuronales
Artificiales (RNA) y Lógica Difusa (LD). En la tabla C.2 se pueden observar las
similitudes y diferencias entre estas dos técnicas. Re-definiendo las motivaciones para crear
los sistemas híbridos neurodifusos, podemos mencionar las siguientes:
•
Los problemas a resolver con estas técnicas inteligentes tienen generalmente una
componente de datos empíricos y otra de conocimiento previo, que con los sistemas
neurodifusos pueden ser explotados a cabalidad mezclando los métodos
cuantitativos y cualitativos de las RNA y la LD respectivamente.
•
La expresión de conocimiento como una base de reglas lingüísticas, enriquecida o
surgida con o a través de datos cuantitativos, es una forma adecuada para hacer
realimentación al usuario de la forma como el sistema realiza las tareas.
•
Habiendo encontrado que la representación del conocimiento como un Sistema
Difuso se acerca a la forma de razonamiento humano, es natural intentar adicionar a
estos sistemas capacidades de aprendizaje, de forma que se emule mejor tal
comportamiento o que se mejoren los resultados obtenidos con el sólo sistema
difuso.
Tabla C.2 Comparativa entre las técnicas de RNA y Lógica Difusa.
CARACTERISTICAS
RNA
Lógica Difusa
Paralelismo
Bueno
Bueno
Dominio
Continuo
Continuo
Linealidad
No lineal
No lineal
Base de Conocimiento
Distribuída en pesos
Distribuída en Base
Reglas
de
Método de Solución
Matemática
mediante
propagación
de
la
información de entrada
Razonamiento
Base de Reglas
la
Numérica
Linguística
Datos empíricos
Conocimiento
Representación
conocimiento
del
Conocimiento explotado
105
sobre
humano
ANEXO C
Fundamentos de lógica difusa, redes neuronales, sistemas neurodifusos y ANFIS
previo
Capacidad
aprendizaje
de
Alta
No tiene - Es una forma
lógica
de
tratamiento
matemático.
Ventajas de los sistemas neurodifusos
La estructura neurodifusa permite el uso de métodos cualitativos y cuantitativos en
la construcción de modelos, en la etapa de aprendizaje, en la de funcionamiento y en la
realimentación de conocimiento al usuario, permitiendo así, todo el conocimiento
disponible. Los métodos cuantitativos que se observan en el aprendizaje que los sistemas
neurodifusos pueden realizar a partir de datos del ambiente y en su forma matemática de
funcionamiento, mientras los métodos cualitativos se reflejan en el sentido lingüístico que
tiene la base de conocimiento de los sistemas difusos y que genera una interacción bilateral
sistema-hombre, permitiendo la introducción de conocimiento previo al sistema y la
realimentación del estado final del modelo en forma de reglas expresadas lingüísticamente
desde el sistema al hombre. Las otras ventajas, son las conocidas ya ampliamente y que
vienen heredadas de los sistemas difusos y de las RNA, tales como interpretación
lingüística, introducción de conocimiento previo, autoaprendizaje, generalización,
interpolación, etc.
Limitaciones de los sistemas neurodifusos
•
Curso de la dimensionalidad: Los sistemas difusos presentan el problema del
crecimiento exponencial del tamaño del modelo respecto al número de variables que
poseen, haciendo impractico su uso para sistemas de más de cuatro dimensiones
•
Calidad de los datos: Existen problemas asociados con la cantidad, distribución y
ruido en los datos. Si los datos están mal distribuidos, el aprendizaje puede no ser
muy bueno, presentando especialmente problemas de generalización de
interpolación si faltan muchos datos en cierta región. Este inconveniente es herencia
de los sistemas neuronales y puede ser superado interpolando los datos, haciendo un
tratamiento previo o buscando una representación adecuada de los mismos.
•
Conocimiento previo: En los sistemas neurodifusos es deseable tener el
conocimiento previo y confiable de un experto en el sistema, pues de otro modo, se
debe realizar un modelado por "Fuerza Bruta" exclusivamente a través de los datos
numéricos empíricos y existirán problemas al no haber descripción cualitativa del
sistema.
106
ANEXO C
Fundamentos de lógica difusa, redes neuronales, sistemas neurodifusos y ANFIS
C.3.1 ANFIS
Es una clase de red adaptiva que es funcionalmente equivalente a un sistema de
inferencia difuso TSK. Este tipo de red usa un procedimiento de aprendizaje híbrido, es
decir utiliza el algoritmo de aprendizaje de gradiente descendente para determinar los
antecedentes del sistema difuso y utiliza mínimos cuadrados para determinar los parámetros
de salida.. Para explicar estos algoritmos se propone el diseño de una red de 2 entradas
(x,y) y una salida (z), cada entrada estara representada por 2 conjuntos difusos, para este
ejemplo se proponen funciones triangulares, se asume que el sistema difuso representado
por esta red tiene 4 reglas, este diseño de red se muestra en la figura C.5 [24].
capa 1
capa 2
capa 3
capa 4
x
A1
a 1, b 1, c 1
Π
A2
a 2, b 2, c 2
Π
x
A3
a 3, b 3, c 3
N
w2
N
w3
Π
y
A4
a 4, b 4, c 4
w1
N
w4
Π
N
w1
w2
w3
w4
capa 5
y
p1, q1, r1
p2, q2, r2
z
p3, q3, r3
p4, q4, r4
x
y
Fig. C.5 arquitectura de una red de 2 entradas, y 1 salida (propagación)
El procedimiento para entrenar la red es el siguiente:
1. Se proponen los parámetros de las funciones triangulares (ai, bi, ci).
2. Propagar los patrones de entrada (x,y) y por medio del método de mínimos
cuadrados, se encuentran los parámetros de los consecuentes pi, qi y ci. Este método
se explica a continuación.
La salida de la red de acuerdo a la relación de las entradas con las reglas TSK es:
z=
4
r =1
w r ( p r x + q r y + rr )
Como son cuatro reglas:
107
(C.1)
ANEXO C
Fundamentos de lógica difusa, redes neuronales, sistemas neurodifusos y ANFIS
z1 = w1 ( p1 x + q1 y + r1 )
z 2 = w 2 ( p 2 x + q 2 y + r2 )
z 3 = w 3 ( p3 x + q3 y + r3 )
z 4 = w 4 ( p 4 x + q 4 y + r4 )
Ordenando de forma matricial se tiene:
p1
q1
r1
p2
z1
z2
z3
=
z4
w1 x w1 y w1
w 2 x w 2 y w2
w3 x w3 y w3 w4 x w 4 y w4
q2
w1 x w1 y w1
w2 x w2 y w 2
w3 x w3 y w3 w4 x w4 y w 4
r2
w1 x w1 y w1
w2 x w2 y w 2
w3 x w3 y w3 w4 x w4 y w 4
p3
w1 x w1 x w1
w 2 x w 2 y w2
w3 x w3 y w3 w4 x w 4 y w4
q3
r3
p4
q4
r4
O bien generalizando:
Z = XC
Donde:
|
Z= Salida Deseada.
X= Patrones de entrenamiento afectado por los antecedentes.
C= Consecuentes.
Lo que interesa es la obtención de los parámetros de los consecuentes, así que aplicando
la definición de mínimos cuadrados [42] se tiene:
[
C = XTX
]
−1
XTZ
3. Inicializar los consecuentes con los valores que se obtienen con mínimos cuadrados.
4. Propagar de nuevo todos los patrones de entrenamiento.
5. Realizar la retropropagacion para encontrar los valores de los antecedentes
(parámetros ai, bi, ci).
Al hablar de redes de retropropagación o redes de propagación hacia atrás hacemos
referencia a un algoritmo de aprendizaje mas que a una arquitectura determinada. La
retropropagación consiste en propagar el error hacia atrás, es decir de la capa de salida
hacia la capa de entrada, pasando por las capas ocultas intermedias y ajustando los
108
ANEXO C
Fundamentos de lógica difusa, redes neuronales, sistemas neurodifusos y ANFIS
pesos de las conexiones con el fin de reducir dicho error. Hay distintas versiones o
reglas del algoritmo de retropropagación y distintas arquitecturas a las que pueden ser
aplicados.
El algoritmo básico de aprendizaje (gradiente descendente) de la red se basa en la
habilidad para cambiar los valores de sus pesos en respuesta al error generado. Durante
el entrenamiento de una red, se pasa cada patrón de entrada a través de las capas de la
red para generar un resultado en cada nodo de salida. Para encontrar el error se resta el
resultado generado por la red al resultado deseado. Después la red propaga hacia atrás, a
las capas ocultas la derivada del error de la salida.
Cada nodo oculto calcula la suma de los errores retropropagados para encontrar la
contribución indirecta al error conocido de la salida. Después de que los errores de la
salida y de cada nodo han sido determinados los nodos ajustan sus pesos para reducir
este error. La ecuación que cambia sus pesos esta diseñada para minimizar las suma de
los errores cuadrados de la red [24]. El gradiente descendente trata de encontrar los
pesos que mejor se ajustan a los patrones y es la base del algoritmo de
retropropagacion, se trata de una regla de aprendizaje supervisado, ya que es preciso
presentar a la red todos los casos de pares entradas-salida que se desea que la red
aprenda. Este método también es conocido como Regla Delta generalizada, por que en
esencia el procedimiento consiste en modificar los pesos de las conexiones (por lo
tanto, favorecer el aprendizaje de la red) a partir del calculo o la diferencia (o delta)
entre las salidas efectivas de la red y las salidas deseadas.
La figura C.6 representa la retropropagacion en la red de dos entradas y una salida
descrita anteriormente, mediante la cual se mostrará el desarrollo matemático del
algoritmo de aprendizaje de la red.
capa 1
capa 2
capa 3
capa 4
x
A1
a 1, b 1, c 1
Π
x
A2
a 2, b 2, c 2
A3
a 3, b 3, c 3
N
w2
Π
N
w3
Π
y
A4
a 4, b 4, c 4
w1
N
w4
Π
N
w1
w2
w3
w4
capa 5
y
p1, q1, r1
∆u1
p2, q2, r2
p3, q3, r3
∆u 2
∆u3
∆u 4
p4, q4, r4
x
y
Fig. C.6 arquitectura de una red de 2 entradas, y 1 salida (retro.propagación)
109
∂E
∂∆u
∆u
ANEXO C
Fundamentos de lógica difusa, redes neuronales, sistemas neurodifusos y ANFIS
De la definición de la regla delta [42]:
∆α = − n∀α E (α )
Corrección
de pesos
=
Factor de
Gradiente
aprendisaje local
(C.3)
(Error )
∂E
∂α i
Suponiendo que α sea cualquiera de los parámetros (ai, bi, ci) de cualquier función de
membresía µ y que E sea la medida del error dada por:
∆α i = − n
(
)
2
1
∆u * − ∆u
2
1
2
Error = (salida deseada − salida real )
2
E=
(C.4)
De acuerdo a la regla, para cualquier parámetro del nodo i en la capa 1 de forma
genérica la razón de cambio para un parámetro después de un patrón de datos
propagado es:
(C.5)
∂E
∆α = − n
∂α
De acuerdo a la regla de la cadena la cual nos permite derivar composiciones de
funciones [referencia] el gradiente se puede expresar como:
(C.6)
∂E ∂E ∂∆u ∂ wi ∂wi ∂µ i
=
∂α ∂∆u ∂ wi ∂wi ∂µ i ∂α
De acuerdo a la estructura de la red de la figura. (C:6) se definen las siguientes
relaciones:
E=
2
1
∂E
∆u * − ∆u
→
= ∆u * − ∆u (− 1)
2
∂∆u
(
∆u =
wi =
)
(
wi ∆u r
→
wi
∂w
→ i =
wi
∂wi
(
)
∂∆ u
= ∆u r
∂ wi
wi − wi
wi )
2
=
wi
(1 − wi )
wi
(C.7)
(C.8)
(C.9)
Según el producto de los antecedentes se tiene:
(C.10)
∂wi
= µi
∂µ i
Sustituyendo las ecuaciones (C.7), (C.8), (C.9), (C.10) en la ecuación (C.6) y
reduciendo se tiene:
wi = µ i µ j
para i ≠ j
→
110
ANEXO C
Fundamentos de lógica difusa, redes neuronales, sistemas neurodifusos y ANFIS
∂E 1
∂µ
=
∆u − ∆u * ∆u r w1 (1 − w1 ) i
∂α µ i
∂α
(
(C.11)
)
Para encontrar el nuevo parámetro a, b ó c de las funciones de membresía de acuerdo a
la ecuación (C.5) se tiene:
∆α = −n
∂E
donde ∆α = ( peso nuevo − peso anterior )
∂α
α A − α P = −n
∂E
∂α
∂E
∂α
De modo que sustituyendo la ecuación (C.11) en la (C.12) tenemos:
∂µ
1
α (k + 1) = α (k ) − n
∆u − ∆u * ∆u r w1 (1 − w1 ) i
µi
∂α
∂µ i
Las derivadas parciales de ∂α se encuentran de acuerdo a la
membresía utilizada. Para este caso definimos funciones de membresía
(figura C.7).
α (k + 1) = α (k ) − n
(
(x )
Triangular
A
µ A (x )
)
µ A( x)
(C.12)
(C.13)
función de
triangulares
A
si x ≤ a
0
x−a
µ = b−a
c−x
c−b
0
si a < x ≤ b
si b < x ≤ c
0
a
si x < c
ó
µ ( x; a , b , c ) = max 0, min
x−a c−x
,
b−a c−b
Parámetros : a , b , c
Figura C.7 Función de membresía tipo triangular.
Finalmente las derivadas son:
111
b
c
x
ANEXO C
∂µ i
=0
∂a
∂µ i
x−b
=
∂a (b − a )2
∂µ i
=0
∂a
∂µ i
=0
∂a
∂µ i
=0
∂b
∂µ i
a−x
=
∂b (b − a )2
∂µ i
c−x
=
∂b (c − b )2
∂µ i
∂b
∂µ i
∂b
∂µ i
∂b
∂µ i
∂b
Fundamentos de lógica difusa, redes neuronales, sistemas neurodifusos y ANFIS
si x ≤ a
si a < x ≤ b
si b < x ≤ c
si x < c
si x ≤ a
si a < x ≤ b
si b < x ≤ c
=0
si x < c
=0
si x ≤ a
=0
si a < x ≤ b
=
x−b
(c − b )2
∂µ i
=0
∂b
si b < x ≤ c
si x < c
112
ANEXO D
Publicación RVP-AI/2004
Publicación RVP-AI/2004
En este anexo se presenta el articulo publicado en la decimoséptima reunión de verano de
potencia, aplicaciones industriales y exposición industrial, celebrada en julio del 2004 en
Acapulco, Guerrero, Este articulo describe los resultados preliminares de este tema de tesis.
113
ANEXO D
Publicación RVP-AI/2004
114
ANEXO D
Publicación RVP-AI/2004
115
ANEXO D
Publicación RVP-AI/2004
116
ANEXO D
Publicación RVP-AI/2004
117
ANEXO D
Publicación RVP-AI/2004
118
ANEXO D
Publicación RVP-AI/2004
119
ANEXO D
Publicación RVP-AI/2004
Referencias
[1] Comisión Federal de Electricidad. Programas de inversiones del sector eléctrico 2003 –
2012. Gerencia de Programación de Sistemas Eléctricos. (noviembre 2003).
http://www.cfe.gob.mx/recursos/publicacion_id47/POISE_PORTAL_CFE_2003.pdf
[2] M. Sanchez, S. DeLara, L.Bahamaca. A fuzzy-logic rule-based speed and load
controller for combustion turbines in power generation. Proceedings of the American
Control Conference. pp. 2659-2664. Anchorage, USA. May 8-10, 2002.
[3] L. Téllez. Prospectiva del sector eléctrico 2000-2009. Informe Secretaria de Energía.
edición de la Subsecretaría de Política y Desarrollo de Energéticos y de la Unidad de
Comunicación Social. (2003)
[4] M. Sánchez, R. Garduño, R. Chávez. Tendencias tecnológicas para el mejoramiento del
desempeño de centrales de ciclo combinado. Boletín IIE, Noviembre – Diciembre del 2001.
[5]M. Sánchez. Aplicación de redes neuronales artificiales al control supervisorio de
turbinas de gas. Proyecto interno, Unidad de Control e Instrumentación, Instituto de
Investigaciones Eléctricas, 1995.
[6] C. Garcia. Gas turbine fuzzy speed control. International Conference on Neural
Networks and Neurocontrol, proceedings 2nd Joint México-USA (1997)
[7] S. DeLara, M. Carretero, R. Garduño, L. Castelo, M. Sánchez. Feedforward and
Neurofuzzy speed control for a turbogas unit. ISA, Chicago, Octuber 2002.
[8] R. Garduño,Y. Villagran, S. DeLara, L. Castelo, M. Sánchez. A neurofuzzy update of PI
controllers for speed control of a turbogas unit.. ISA Powid Conference, San Diego, July
2001.
[9] R. Garduño, K. Lee. Wide range operation of a power unit via feedforward fuzzy
control. Departament of Electrical Engineering, The Pennsylvania State University, IEEE
Transactions on Energy Conversion, Vol. 15, No. 4, December 2000.
[10] F. Jurado, M. Blas, M. Castro, J. Carpio. Neural networks and fuzzy logic in electrical
engineering. Department of Electrical Engineering, University of Jaen. IEEE Porto Power
Tech Conference. Porto, Portugal, September 2001.
[11] M. Mihuc. Gas turbine control system modernization: planning, design and
implementation. Paper ISA, 92-0627, 1992.
[12] Westinghouse Electric Corporation Gas Turbines Systems Division. Gas Turbine
Systems Primer, An Introduction to Gas Turbines, Combined Cycles and Gasification
Processes, Lester Pennsylvania. October 1975.
120
ANEXO D
Publicación RVP-AI/2004
[13] M. Ramírez. Modernización del control de velocidad, potencia y temperatura de una
unidad turbogas. Trabajo de tesis, Instituto Politécnico Nacional. México D.F. 1996.
[14] M. Delgadillo, M. Hernández. Modelling and Dynamic Simulation of a gas turbine.
Paper ISA Powid Conference 2002.
[15] M. Hernández, M. Delgadillo. Adecuación del modelo prototipo de turbina de gas al
modelo Hitachi (Ge-5001). Proyecto 11184 “Programación del Controlador Apacs de
Moore”. Unidad de Control e Instrumentación. División Sistemas de Control. Docto IIE11184-DOC-04-2.00Enero 1999.
[16] R. Garduño, M. Sánchez, S.DeLara, M. Carretero; “Control neurodifuso retroprealimentado para la operación en rango amplio de unidades turbogas. Proyecto de
infraestructura No. 11983, Gerencia de Control e Instrumentación, División de Sistemas
de Control 2002.
[17] Y.Tani, T. Iwamiya, S. Takahashi. Advanced control system for gas turbine and
combined cycle power plants. Hitachi Review, Vol. 38, No. 3, 1989.
[18] M. Arreola, S. DeLara, Z. Flores. Especificación Funcional del Prototipo Turbogas-II
(W-191G). Reporte interno, Unidad de Control e Instrumentación. División Sistemas de
Control, IIE,1996.
[19] M. Carretero, S. DeLara, R. Garduño, D. Libreros. Sistema para desarrollo y
validación de algoritmos de control para turbinas de gas. RVP-AI/2002. IEEE, Acapulco
Guerrero.
[20] D. Naucke, F. Klawon. Fundations of Neurofuzzy Systems. John Wiley & Sonn Inc,
Paris Francia, 1997
[21] M Sugeno. An introduction survey of fuzzy control. Inform. Sci. Vol. 36, No. 1 págs.
59-83, (1985).
[22] H. Takagi., Hayashi. NN-driven fuzzy reasoning. Int. Appoximate Reasoning. I. Vol.
5, N0. 3, págs. 191-212, (1991).
[23] Halgamuge, M. Glesner M. The fuzzy neural controller FuNe II with a new adaptive
defuzzification strategy based on CBAD distribution. In European Congress on Fuzzy and
Intelligent Technologies’93. Aachen Alemania. Vol. 2, págs. 665-685.
[24] J-S R. Jang. ANFIS: Adaptive-Network-Based-Fuzzy-Inference. IEEE Trans. On
Systems, Man, and Cybernetics, may 1993.
[25] Dan Hammerstron, Adaptive Solution Inc. Working with Neural Network. IEEE
Spectrum, July 1993.
121
ANEXO D
Publicación RVP-AI/2004
[26] J.S.R. Jang, N. Gulley, Natick. Fuzzy Logic Toolbox. MS, Mathworks, 2000.
[27] K. Ogata. Ingeniería de Control Moderna. segunda edición, Prentice Hall
Hispanoamérica, 1993.
[28] B. C. Kuo. Sistemas de Control Automatico .septima edición, Prentice Hall
Hispanoamérica, 1996.
[29] L-X. Wang. A course in fuzzy systems and control. Prentice Hall, Upper Saddle River,
NJ,1997.
[30] T. Takagi and M. Sugeno. Fuzzy identification of systems and its applications to
modeling and control. IEEE Trans. On Systems, Man, and Cybernetics, 15:116-132, 1985.
[31] M.Sugeno, editor. Industrial applications of fuzzy control. Elservier Science Pub. Co.,
1985.
[32] W. Pedrycz. Fuzzy control and fuzzy systems. Wiley, New York, 1989
[33] A. Kandel. Fuzzy expert systems. Addison-Wesley, 1988.
[34] A. Kandel, editor. Fuzzy expert systems. CRC Press, Boca Raton, FL, 1992.
[35] L.A. Zadeh. Fuzzy sets. Information and Control, 8:338-353, 1965.
[36] L.A. Zadeh. Outline of a new appoach to the analisis of complex systems and decision
processes. IEEE Trans. On Systems, Man, and Cybernetics, 3(1):28-44, January 1973.
[37] T. Takagi and M. Sugeno. Derivation of fuzzy control rules from human operator´s
control actions. Proc. of the IFAC Symp. on Fuzzy Information, Knowledge Representation
and Decision Analysis, pages 55-60, July 1983.
[38] C.-C. Lee. Fuzzy logic in control systems: fuzzy logic controler-part 1. . IEEE Trans.
On Systems, Man, and Cybernetics, 20(2):404-418,1990.
[39] C.-C. Lee. Fuzzy logic in control systems: fuzzy logic controler-part 2. . IEEE Trans.
On Systems, Man, and Cybernetics, 20(2):419-435,1990.
[40] P. K. Simpson. Artificial Neural Systems. Pergamon Press,1990.
[41] J-S. Roger Jang, C.-T. Sun, E. Mizutani. Neuro-Fuzzy and Soft Computing. Prentice
Hall, Upper Saddle River, NJ,1997.
[42] S. Haykin. Neural Networks A Comprehensive Foundation. Prentice Hall, Upper
Saddle River, NJ,1999.
122