2 - RUA
Anuncio

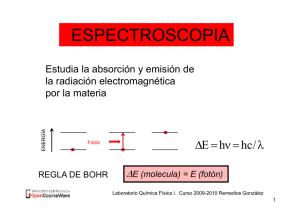
Química Física Avanzada II Tema 3. Interacción materia-radiación 3.1. Concepto de Espectroscopía Línea de absorción Ej E j En h E= h En E j En hc Absorción E j En Frecuencia hc 3.1. Concepto de Espectroscopía Separación de energías en una molécula E E r E v Ee E AJ B vC n Rotación E = 0.04 kJ/mol = Vibración E = 20 kJ/mol = 1750 cm-1 Electrónica E = 840 kJ/mol = 70000 cm-1 3,5 cm-1 3.1. Concepto de Espectroscopía Regiones del espectro electromagnético Zona Radiofrecuencias 10 cm 1000 cm 0,1 cm-1 0,001 cm-1 Microondas 0,1 cm 10 cm 10 cm-1 0,1 cm-1 Infrarrojo 0,8 1000 12500 cm-1 10 cm-1 Visible 4000 Å 8000 Å 25000 cm-1 12500 cm-1 Ultravioleta 100 Å 4000 Å 106 cm-1 25000 cm-1 Rayos 1Å 100 Å 108 cm-1 106 cm-1 Rayos 0,01 Å 1Å 1010 cm-1 108 cm-1 3.1. Concepto de Espectroscopía Experimento de absorción RENDIJA FUENTE CÉLULA RENDIJA DISPERSOR DETECTOR REGISTRO 3.1. Concepto de Espectroscopía Características instrumentales Poder de resolución Poder de resolución = Sensibilidad Cantidad de muestra Acumulación de espectros 3.1. Concepto de Espectroscopía Intensidad de la línea espectral Magnitud de la interacción materia-radiación Probabilidad de la transición Población de los estados energéticos ni N Ley de distribución de Boltzmann J 0 1 0 0 v 0 0 1 0 n 0 0 0 1 Energía 0,00 0,04 20,00 840,00 gi e Ei KT Ei KT g e i i ni g i E i 0 e n0 g0 Población 1 2,9 2,3 10-4 2 10-146 KT 3.2. Interacción radiación electromagnética-sistema molecular Radiación planopolarizada x x E 0 x 2 r 0 r r z E i E x i E x cos 2 t - 2 8 E z B y r 0 r r z B j B y j B y cos 2 t - 2 3.2. Interacción radiación electromagnética-sistema molecular Sistema molecular r qi ri r Interacción r r V E Hˆ E x x E y y E z z z 0 ˆ H E x cos 2 t - 2 x Hˆ x E x0 cos t 2 3.2. Interacción radiación electromagnética-sistema molecular Transición espectroscópica 0j an n0 a j 0j Hˆ x E x0 cos t n0 i 0 ˆ 0 H j n d h dt da j i 0 iE j t / h 0 0 iEn t / h cos e E t dx j x x ne h dt da j i inj t 0 e E x cos t j0 xn0 dx dt h da j x nj dx 0 j 0 x n j a aj nj E j E 0 x h2 En h 2 2 x nj 2 2t nj 3.2. Interacción radiación electromagnética-sistema molecular Probabilidad de transición j a aj E 0 x h x 2 2 x nj 2 t 2 Para radiación isotrópica 2 2 a a j 2 nj t 3h j 2 Bnj 2 nj 3h 2 a a j Bnj t j E x0 8 2 2 x 2 a a j 2 nj t x h j x y z 1 3 2 nj x nj 2 y nj 2 z nj Coeficiente de Einstein para la absorción inducida de radiación 2 2 Pnj 2 nj Bnj 3h 2 3.3. Probabilidades de transición de Einstein Coeficientes de probabilidad Para absorción inducida Pnj Bnj Para emisión inducida Pjn B jn A jn Para emisión espontánea Significado físico de Ajn dN j dt 8 h 3jn c 3 Ajn N j B jn 3 3c h N j N j0e 1 A jn Vida media del estado j 32 3 3jn jn A jn t 2 3.4. Reglas de selección Integral del momento de transición Si nj j0 ˆ n0 d 0 Pnj 0 Condiciones para que la transición n j sea permitida Si nj j0 ˆ n0 d j0n0 d 0 cte Traslación constante No hay espectro Rotación debe variar en dirección Vibración debe variar en módulo Reglas de selección Restricciones que hay que imponer a los valores de los números cuánticos n y j para que la integral del momento de transición n j sea distinta de cero 3.4. Reglas de selección Ejemplo: Partícula en una caja monodimensional 1 2 2 n x n sin a a sin sin qx q n x n x 2 x sin sin a dx a0 a a x nn 1 cos cos 2 a n n x q x nn x cos a 0 a n n x cos dx a u cos u du cos u u sin u x nn q a cos n n 1 cos n n 1 2 2 2 n n n n n 2 m 1 m 0 , 1, 2, ... 3.5. Forma y anchura de las líneas Anchura natural E t h I 0 2 a ( n1 j 1 )2 16 2 I 0 Para n= y como a 0 2 2 j-1=Ajn: 1 n1 j 1 2 Ajn 2 2 3.5. Forma y anchura de las líneas Efecto Doppler 1 v c 1 v c Efecto de la concentración I Lorentz(x) Gauss(x) 0 Efecto de saturación a 0 2 I a e 2 2 0 2 2 2 3.6. Comparación con datos experimentales Ley de Lambert-Beer d 0 dI I c d l I T I l dI c d l I I0 0 I ln c l I0 I0 A ln T ln I I0 A c l 3.6. Comparación con datos experimentales Resultados teóricos Intensidad de la radiación Flujo de energía que atraviesa una superficie de 1 cm2 en un segundo I = v 1 cm dI Pnj h n dl Pnj 2 dI 2 nj 3h d NA nc 1000 2 2 2 nj 2 3h I h n d l v 2 h N 2 A I c dl dI 2 nj v 1000 3h 2 h N 2 A 2 nj v 1000 3h