Clase 1 - Facultad de Ciencias Exactas
Anuncio

TEORÍA DE LA INFORMACIÓN
Repaso de Probabilidades y Estadística
Muestreo computacional
continuación
INGENIERÍA DE SISTEMAS
Cursada 2016
VARIABLE ALEATORIA o ESTOCÁSTICA
Es una función F definida sobre un espacio de probabilidad, que asigna un
valor (generalmente numérico) al resultado de un experimento aleatorio
F se define por el conjunto de posibles valores que puede tomar (discretos
o continuos) y una distribución de probabilidad sobre ese conjunto
se tiran 2 dados
E= {11, 12, 13, 14, 15, 16, 21, 22, 23, 24, 25, 26,
31, 32, 33, 34, 35, 36, 41, 42, 43, 44, 45, 46,
51, 52, 53, 54, 55, 56, 61, 62, 63, 64, 65, 66}
A partir de las salidas experimentales se define la variable aleatoria (v.a.):
S = suma de los valores de los 2 dados S = { 2, 3, 4, 5, … , 12}
Función distribución de probabilidad
P(S=s) Cuál es la probabilidad de que la v. a. S tome un valor s?
P(S) = { 1/36, 2/36, 3/36, 4/36, …., 1/12 }
Teoría de la Información 2016 - Facultad de Ciencias Exactas- UNCPBA
1
VARIABLE ALEATORIA o ESTOCÁSTICA
S = suma de los dados
S=
2
3
4
5
6
7
8
9
10
11
12
P(S)=
1/36
2/36
3/36
4/36
5/36
6/36
5/36
4/36
3/36
2/36
1/36
12
1
p(S ) 36 (1 2 3 4 5 6 5 4 3 2 1) 1
Función acumulada de probabilidades F(x)
es continua y creciente con máximo 1
x 2
Distribución de probabilidad (discreto) donde
x2
F ( x2 ) F ( x1 ) p( x)
p( x) 1
x
Función de densidad de probabilidad (continuo)
donde
f ( x)dx 1
F ( x2 ) F ( x1 )
(discreto)
x x1
x2
f ( x)dx
(continuo)
x x1
x
Teoría de la Información 2016 - Facultad de Ciencias Exactas- UNCPBA
VARIABLE ALEATORIA o ESTOCÁSTICA
E= {11, 12, 13, 14, 15, 16, 21, 22, 23, 24, 25, 26,
31, 32, 33, 34, 35, 36, 41, 42, 43, 44, 45, 46,
51, 52, 53, 54, 55, 56, 61, 62, 63, 64, 65, 66}
Se definen 2 v.a.:
S = suma de los dados
D = 0 si son iguales, 1 si son distintos
P(S/D)= P(S,D)/P(D)
P(S,D)
S \ D
0
1
P(S)
2
1/36
0
1/36
3
0
2/36
4
1/36
5
6
7
8
9
10
11
12
P(D)
P(D/S)= P(S,D)/P(S)
0
1
0
1
2
1/6
0
2
1
0
2/36
3
0
2/30
3
0
1
2/36
3/36
4
1/6
2/30
4
1/3
2/3
0
4/36
4/36
5
0
4/30
5
0
1
1/36
4/36
5/36
6
1/6
4/30
6
1/5
4/5
0
6/36
6/36
7
0
6/30
7
0
1
1/36
4/36
5/36
8
1/6
4/30
8
1/5
4/5
0
4/36
4/36
9
0
4/30
9
0
1
1/36
2/36
3/36
10
1/6
2/30
10
1/3
2/3
0
2/36
2/36
11
0
2/30
11
0
1
1/36
0
1/36
12
1/6
0
12
1
0
1/6
S
D
S
D
5/6
Teoría de la Información 2016 - Facultad de Ciencias Exactas- UNCPBA
2
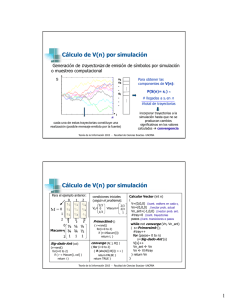
MUESTREO COMPUTACIONAL
para encontrar una distribución de probabilidad
float CalcularProbDS()
{
int tiradas=0;
int exitos [2][12] inicializada en 0
float probDS_ant [2][12] inicializada en -1
float probDS_act [2][12] inicializada en 0
while not converge (probDS_ant, probDS_act)
{ x=Arrojardado(); y=Arrojardado();
D= (x!=y);
S= x+y;
exitos [D,S]++;
tiradas++;
for (i=0 to 1)
for(j=2 to 12)
{ probDS_ant [i,j]= probDS_act [i,j];
probDS_act [i,j]= exitos [i,j] / tiradas;
}
}
return probDS_act;
}
int Arrojardado ()
{
probacum={1/6,2/6,3/6,4/6,5/6,1}
p=rand () ;
for (i=1 to 6)
if (p <probacum[ i ])
return i;
}
BOOL converge(Pant, Pact)
{
for (i=0 to 1)
for (j=2 to 12)
if (|Pant [i,j] – Pact[i,j]| )> )
return false;
return true;
}
cte. pequeña
Teoría de la Información 2016 - Facultad de Ciencias Exactas- UNCPBA
GENERACIÓN DE VARIABLE ALEATORIA
Generar valores de una variable aleatoria X con determinada distribución de
probabilidad generar función de probabilidad acumulada
F(x) 1
Se obtiene una muestra de
valores independientes de X
con la distribución buscada
rand() p
0
x
x=F-1(p)
Ejemplo v.a. discreta
int Arrojardado ()
{ probacum={1/6,2/6,3/6,4/6,5/6,1}
p=rand () ;
for (i=1 to 6)
if (p<probacum[i])
return i;
}
F(X)
1
p
0
X
1 2 3 4 5 6
Teoría de la Información 2016 - Facultad de Ciencias Exactas- UNCPBA
3
GENERACIÓN DE VARIABLE ALEATORIA
f(x)
Ejemplo v.a continua
f(x)=2x
int generarX ()
{
U= rand ()
x= sqrt (U) //función en el ejemplo
return x
}
0
1
F (1) F (0)
x 1
x 0
x
F ( x) F (0) 2 x dx x
1
2 x dx x 2 1
0
F(x) 1
2
0
U
U x2 x U
0
x U
1
Teoría de la Información 2016 - Facultad de Ciencias Exactas- UNCPBA
INDICADORES
Promedio o media
Caso discreto:
X x p ( x)
Caso continuo:
x
X x f ( x)dx
x
Se arrojan 3 monedas
y se cuenta el número de caras
X= {0,1,2,3} ; p(x)={1/8,3/8,3/8,1/8}
1
X= [0..1] ; f(x)=2x
f(x)
f(x)=2x
p(x)
0
0
1
2
3
x
<X>=0*1/8+1*3/8+2*3/8+3*1/8=12/8= 1.5
1 x
0
X
x 1
x 0
1
2
x 2 x dx x 3 2 / 3
3 0
Teoría de la Información 2016 - Facultad de Ciencias Exactas- UNCPBA
4
INDICADORES
Desvío estándar
Varianza
( x X ) p ( x )
2
x
2
x x2
x
( x 2 2 x X X 2 ) p ( x)
x
x 2 p ( x) 2 X x p ( x) X 2 p ( x)
x
x
x 2 X X
2
2
x 3 / 4 0.86 caras
x
2
dispersión de los datos alrededor de la media
x2 x 2 X 2
X= {0,1,2,3} ; p(x)={1/8,3/8,3/8,1/8}
x2 ( x X ) 2 p ( x)
x
(0 1.5) 2 *
1
1
... (3 1.5) 2 *
8
8
3
caras 2
4
Teoría de la Información 2016 - Facultad de Ciencias Exactas- UNCPBA
Media por muestreo
computacional
X
INDICADORES
x
i
i
N
float CalcularMedia ()
{
suma=0;
tiradas=0;
media_ant=-1;
media_act= 0;
; N es el número de muestras
2,5
2
1,5
1
0,5
0
while not converge (media_ant,media_act)
{
x=generarX ();
suma=suma+x;
tiradas++;
media_ant=media_act;
media_act=suma/ tiradas
}
return media_act
}
0
500
1000
1500
2000
2,5
2
1,5
1
0,5
0
1
10
100
1000
Teoría de la Información 2016 - Facultad de Ciencias Exactas- UNCPBA
5
INDICADORES - Resumen
Cálculo Analítico
Muestreo computacional
x p( x)
X x
x f ( x)dx
x
Media
X
Varianza
2
x
( x X ) 2 p ( x )
x
i
i
N
xi
2
xi
2
(x N )
i
x
x2
x 2 X 2
2
x
Desvío estándar
x x2 x 2 X 2
i
i
N
(x N )
i
x
i
i
N
N es el número de muestras
Teoría de la Información 2016 - Facultad de Ciencias Exactas- UNCPBA
RELACIÓN ENTRE 2 V. A.
• Dadas dos variables aleatorias A y B (discretas o continuas) es posible analizar
si existe relación entre ellas
• Una forma de estudiar la relación entre dos variables es observar la tabla de
distribución conjunta P(A,B) puede ser dificultoso
• Si a partir de la distribución conjunta p(AB), en el plano se establece un punto
por cada par (A,B) con p(AB) > 0
puede generarse una nube de puntos diagrama de dispersión
relación lineal, exponencial, logarítmica … o sin relación
Diagrama de dispersión:
Teoría de la Información 2016 - Facultad de Ciencias Exactas- UNCPBA
6
RELACIÓN ENTRE 2 V. A.
Covarianza y Correlación
La covarianza y la correlación permiten cuantificar la relación (lineal) que
hay entre las variables analizadas
Covarianza
CovAB ( A A )( B B ) p ( AB)
A
B
A B p ( AB) B A p ( AB) A B p ( AB) A B p ( AB)
A
B
A
B
B
A
A
B
AB B A A B A B AB A B
Correlación AB
A B p( AB)
A
B
• La Cov(A,B) se utiliza para cuantificar la relación entre las variables A y B Compara
con los valores medios de cada variable.
• Desventaja: El valor obtenido es una cantidad no acotada y depende de las unidades de
las variables (se dificulta la relación entre las variables es alta o no)
Teoría de la Información 2016 - Facultad de Ciencias Exactas- UNCPBA
RELACIÓN ENTRE 2 V. A.
Covarianza y Correlación
Por muestreo computacional
Covarianza
Cov AB
Correlación
AB A B
i
i
N
i
i
i
N
i
*
i
AB
N
AB
i
i
i
N
AI es el valor de A obtenido en la i-ésima tirada
BI es el valor de B obtenido en la i-ésima tirada
N es el número de experimentos
Teoría de la Información 2016 - Facultad de Ciencias Exactas- UNCPBA
7
RELACIÓN ENTRE 2 V. A.
Coeficiente de correlación lineal
rAB
Cov AB
A B
AB A B
A A 2 * B 2 B 2
2
•
Indica el grado de acople entre las v.a. A y B (grado de información que A aporta sobre B)
•
Ventaja: rAB tiene el mismo signo (positivo o negativo) que la CovAB , pero es adimensional
rAB=1
-1 ≤ rAB ≤ 1
A y B totalmente correlacionadas en forma positiva
existe dependencia funcional lineal directa entre A y B
(línea recta creciente en el diagrama de dispersión)
rAB=-1 Totalmente correlacionados en forma negativa
existe dependencia funcional inversa entre A y B
(línea recta decreciente el diagrama de dispersión)
rAB 0 Las variables tienen poca o nula relación lineal
Conocer una variable aporta poca (o nada de) información sobre la otra
Nota:
•
•
Si A y B son independientes, entonces CovAB = 0 (y rAB = 0)
Si CovAB = 0 entonces no tienen relación lineal (pero podrían tener otro tipo de relación y no ser indep.
usar otro tipo de métrica más apropiada)
Teoría de la Información 2016 - Facultad de Ciencias Exactas- UNCPBA
RELACIÓN ENTRE 2 V. A.
Se tienen 2 v.a. A y B (distancias en mm) con distribución:
P(A,B)
B
B\ A
0
1
2
3
P(B)
0
1/8
0
0
0
1/8
1
0
3/8
0
0
3/8
2
2
3/16
0
3/16
0
3/8
1
1/8
0
3
0
3/32
0
1/32
P(A)
5/16
15/32
3/16
1/32
A
A2 A
2
0.788mm
<B>=1.5 mm
B
B B
2
0.866mm
AB 1.68mm
nube de puntos
ascendente
0
<A>= 0.93 mm
2
3
1
2
3
A
2
Cov AB AB A B 0.28mm 2
rAB Cov AB / A B 0.41
la tendencia es lineal ascendente (si A crece, B crece)
moderadamente correlacionados en forma positiva
Interpretación: Conocer el resultado de una v.a. aporta
41% de información sobre la otra
Teoría de la Información 2016 - Facultad de Ciencias Exactas- UNCPBA
8
RELACIÓN ENTRE 2 V. A.
Regresión lineal
Cuando una distribución (A, B) sigue una tendencia lineal ascendente o descendente
se puede definir la recta que mejor se ajusta a la nube de puntos
a partir de la ecuación de la recta dado un valor de X se puede estimar el valor de
la variable Y, como si se tratara de una función
B
B= c1 A+ c2
A
Teoría de la Información 2016 - Facultad de Ciencias Exactas- UNCPBA
RELACIÓN ENTRE 2 V. A.
Regresión lineal
Medida del error (por aproximar):
E ( B´ B ) 2 p ( AB ) donde B´= c1*A+c2 es el valor estimado de B
A
B
A
B
E (c1 * A c2 B ) 2 p ( AB ) E (c1 , c2 )
Se busca c1 y c2 que minimicen la función de error E:
E / c1 0 ; E / c2 0
Obteniéndose:
c1
AB A B Cov AB
( A 2 A 2 )
A2
c2 B c1 A
B= 0.45 A+ 1.08
B
3
2
c1 0.28 / 0.7882 0.45
1
c2 1.5 0.45 * 0.93 1.08
0
0
1
2
3
A
Teoría de la Información 2016 - Facultad de Ciencias Exactas- UNCPBA
9
RELACIÓN ENTRE 2 V. A.
Estimación probabilística
Se trata de estimar el valor de una v.a. en función de otra, buscando el menor error promedio
estimar el valor de B a través de una función g(A) y calcular el error:
E ( B g ( A)) 2 p ( A, B )
A
B
A
B
( B g ( A)) 2 p ( A) p ( B / A)
p ( A)
A
( B g ( A))
2
p ( B / A)
B
(B-g(A)) ≥ 0; p(A) ≥ 0; p(B/A) ≥ 0 buscar el mínimo de cada sumando (porque todos son positivos)
si llamamos : B ´= g(A) y Π (B)= p(B/A)
g ( B) ( B B´)2 ( B)
minimizar la función
B
g ( B) / B (2 B´2 B) ( B) 2 B´ 2 B ( B) 0
B
B
B´ B ( B) B´ g ( A) B p ( B / A)
B
Es la mejor estimación de B en
función de A (minimiza el error)
B
Teoría de la Información 2016 - Facultad de Ciencias Exactas- UNCPBA
RELACIÓN ENTRE 2 V. A.
Estimación probabilística
P(A,B)
B
A
P(B/A) = P(A,B)/P(A)
0
1
2
3
0
1
2
3
0
1/8
0
0
0
0
2/5
0
0
0
1
0
3/8
0
0
1
0
4/5
0
0
2
3/16
0
3/16
0
2
3/5
0
1
0
3
0
3/32
0
1/32
3
0
1/5
0
1
P(A)
5/16
15/32
3/16
1/32
Estimar B’ a partir de A: B' g ( A)
B
A
B p( B / A)
Estimación B/A
B
A
B´
0
2/5*0+3/5*2= 6/5 = 1,2
1
4/5*1+1/5*3 = 7/5 =1,4
2
1*2 = 2
1
3
1*3 = 3
0
3
2
Regresión lineal
0
1
2
3
A
Teoría de la Información 2016 - Facultad de Ciencias Exactas- UNCPBA
10
RELACIÓN ENTRE 2 V. A.
Estimación probabilística
Estimación B´ dado A
B
Estimar B’ a partir de A
3
B' g ( A) B p( B / A)
2
1
B
0
0
1
Estimar A’ a partir de B
2
3
A
Estimación A´ dado B
A' g ( B) A p( A / B)
B
A
3
2
1
0
0
1
2
3
A
Teoría de la Información 2016 - Facultad de Ciencias Exactas- UNCPBA
RELACIÓN ENTRE 2 V. A. - Resumen
Cálculo Analítico
Covarianza
Estimación
CovAB AB A B
B' g ( A) B p( B / A)
B
A' g ( B) A p( A / B)
A
Muestreo computacional
ai bi ai b j
CovAB
i
j
B' g ( A)
A' g ( B)
i
j
N
b
i
i
NA
ai
i
NB
Regresión Lineal
B c1 A c2 ; c1
Cov( A, B)
A c1 B c2 ; c1
Cov( A, B)
A2
B2
; c2 B c1 A
; c2 A c1 B
Obtener constantes c1 y c2
por muestreo comp.
de la Covarianza y Varianza
N es el número de muestras
NA = número de ocurrencias de A
NB = número de ocurrencias de B
Teoría de la Información 2016 - Facultad de Ciencias Exactas- UNCPBA
11
BIBLIOGRAFÍA
Cover T., Thomas J., Elements of Information Theory, 2nd ed.,
John Wiley & Sons, 2006
Papoulis A., Probability Random Variables and Stochastic Processes,
McGraw-Hill, 1991
12