Document
Anuncio

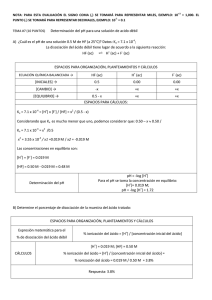
Ácidos y Bases Tema 5 ! ! " # $ # % & # '" ( ) ! % " % % + , % ./ 1 * # ( # " ' ) * 0.% # 0 Definición de ácido Ácido de Arrhenius es una sustancia que produce H+ (H3O+) en agua Ácido de Brønsted es un donador de protones (H+) Ácido de Lewis es una sustancia que acepta un par de electrones Base de Lewis es una sustancia que dona un par de electrones •• + •• OH•• ácido base H+ •• H O H •• H ácido N H •• H+ + H base H H + N H H 15.12 Ácidos y Bases de Lewis H + F B N H •• F F H ácido base F F B F H N H H ¡No se donan o aceptan protones! 15.12 pH – Una medida de la acidez pH = -log [H+] A 250C Disolución neutra [H+] = [OH-] [H+] = 1 x 10-7 pH = 7 ácida [H+] > [OH-] [H+] > 1 x 10-7 pH < 7 básica [H+] < [OH-] [H+] < 1 x 10-7 pH > 7 pH [H+] 15.3 pOH = -log [OH-] [H+][OH−] = Kw = 1.0 x 10-14 −log [H+] – log [OH−] = 14.00 pH + pOH = 14.00 15.3 El pH de la lluvia recogida en una región industrializada un día particular fue 4.82. ¿Cuál es la concentración de ion H+ en el agua de lluvia? pH = -log [H+] [H+] = 10-pH = 10-4.82 = 1.5 x 10-5 M La concentración de ion OH− en una muestra de sangre es 2.5 x 10-7 M. ¿Cuál es el pH de la sangre? pH + pOH = 14.00 pOH = -log [OH-] = -log (2.5 x 10-7) = 6.60 pH = 14.00 – pOH = 14.00 – 6.60 = 7.40 15.3 Ácido fuerte Ácido débil 15.4 15.4 ¿Cuál es el pH de una disolución de HNO3 2 x 10-3 M? HNO3 es un ácido fuerte – se disocia al 100%. HNO3 (ac) + H2O (l) Inicio 0.002 M Final 0.0 M H3O+ (ac) + NO3- (ac) 0.0 M 0.0 M 0.002 M 0.002 M pH = -log [H+] = -log [H3O+] = -log(0.002) = 2.7 ¿Cuál es el pH de una disolución de Ba(OH)2 1.8 x 10-2 M? Ba(OH)2 es una base fuerte – se disocia al 100% Ba(OH)2 (s) Ba2+ (ac) + 2OH- (ac) Inicio 0.018 M Final 0.0 M 0.0 M 0.018 M 0.0 M 0.036 M pH = 14.00 – pOH = 14.00 + log(0.036) = 12.56 15.4 Ácido débil (HA) y su constante de acidez HA (ac) + H2O (l) H3O+ (ac) + A- (ac) H+ (ac) + A- (ac) HA (ac) Ka = [H+][A-] [HA] Ka es la constante de acidez Ka Fuerza del ácido débil 15.5 15.5 ¿Cuál es el pH de una disolución de HF 0.50 M (a 250C)? +][F-] [H = 7.1 x 10-4 Ka = HF (ac) H+ (ac) + F- (ac) [HF] HF (ac) H+ (ac) + F- (ac) Inicial (M) 0.50 0.00 0.00 Cambio (M) −x +x +x x x Equilibrio (M) Ka = Ka ≈ 0.50 − x x2 = 7.1 x 10-4 0.50 - x x2 0.50 = 7.1 x 10-4 [H+] = [F-] = 0.019 M [HF] = 0.50 – x = 0.48 M Ka << 1 0.50 – x ≈ 0.50 x2 = 3.55 x 10-4 x = 0.019 M pH = -log [H+] = 1.72 15.5 ¿Cuándo puedo usar la aproximación? Ka << 1 0.50 – x ≈ 0.50 Cuando x es menor que el 5% del valor del que es substraido. x = 0.019 0.019 M x 100% = 3.8% 0.50 M Menos del 5% Aproximación ok! ¿Cuál es el pH de una disolución de HF 0.05 M HF (at 250C)? x2 = 7.1 x 10-4 x = 0.006 M Ka ≈ 0.05 0.006 M x 100% = 12% 0.05 M Más del 5% Aproximación mala. Debemos encontrar x resolviendo la ecuación cuadrática o el método de las aproximaciones sucesivas. 15.5 Resolución de problemas con ácidos débiles: 1 Identificar las especies que pueden afectar al pH. En la mayoría de los casos se puede ignorar la autoionización del agua. Ignorar [OH−] porque se determinan a partir de [H+]. 2 Usar ICE para expresar las contraciones en términos de sólamente una x desconocida. 3 Escribir Ka en función de las concentraciones en el equilibrio. Despejar x usando el método aproximado. Si la aproximación no es válida, resolver la ecuación exactamente. 4 Calcular las concentraciones de todas las especies y/o pH de la disolución. 15.5 ¿Cuál es el pH de una disolución 0.122 M de un ácido cuya Ka is 5.7 x 10-4? HA (ac) H+ (ac) + A- (ac) Inicial (M) 0.122 0.00 0.00 Cambio (M) -x +x +x 0.122 - x x x Equilibrio (M) x2 = 5.7 x 10-4 Ka = 0.122 - x Ka ≈ x2 = 5.7 x 10-4 0.122 0.0083 M x 100% = 6.8% 0.122 M Ka << 1 0.122 – x ≈ 0.122 x2 = 6.95 x 10-5 x = 0.0083 M Más del 5% Approximación mala. 15.5 x2 = 5.7 x 10-4 Ka = 0.122 - x ax2 + bx + c =0 x = 0.0081 HA (ac) x2 + 0.00057x – 6.95 x 10-5 = 0 -b ± √b2 – 4ac x= 2a x = - 0.0081 H+ (ac) + A- (ac) Inicial (M) 0.122 0.00 0.00 Cambio (M) -x +x +x 0.122 - x x x Equilibrio (M) [H+] = x = 0.0081 M pH = -log[H+] = 2.09 15.5 Grado de ionización = Concentración de ácido ionizado en el eq. Concentración inicial del ácido x 100% Para un ácido monoprótico HA Grado de ionización= HA (ac) , 2 ,% −x 2*4 - 2*2α α5 4 2 [H+] x 100% [HA]0 = concentración inicial [HA]0 H+ (ac) + A- (ac) 3 3 +x +x 4 4 2α 2α 2α 2α 2α7 5 6 5 8*α 2*2α 15.5 Bases débiles y constante de basicidad NH3 (ac) + H2O (l) NH4+ (ac) + OH- (ac) [NH4+][OH-] Kb = [NH3] Kb es la constante de basicidad Kb fuerza de la base débil Resuelve los problemas con bases débiles como los de ácidos débiles, excepto que buscas [OH−] en lugar de [H+]. 15.6 15.6 Constantes de ionización de pares conjugados Ácido-Base HA (ac) A- (ac) + H2O (l) H2O (l) H+ (ac) + A- (ac) OH- (ac) + HA (ac) H+ (ac) + OH- (ac) Ka Kb Kw KaKb = Kw Ácido débil y su base conjugada Kw Ka = Kb Kw Kb = Ka 15.7 15.8 Propiedades ácido-base de las sales Disoluciones neutras: Sales que contienen un metal alcalino o alcalinotérreo (excepto Be2+) y la base conjugada de un ácido fuerte (e.g. Cl-, Br-, y NO3-). NaCl (s) H2O Na+ (ac) + Cl- (ac) Disoluciones básicas: Sales derivadas de una base fuerte y un ácido débil. NaCH3COOH (s) CH3COO- (ac) + H2O (l) H2O Na+ (ac) + CH3COO- (ac) CH3COOH (ac) + OH- (ac) 15.10 Propiedades ácido-base de sales Disoluciones ácidas: Sales derivadas de un ácido fuerte y una base débil. NH4Cl (s) NH4+ (ac) H2O NH4+ (ac) + Cl- (ac) NH3 (ac) + H+ (ac) 15.10 Hidrólisis con Al3+ 15.10 Propiedades ácido-base de sales Disoluciones de sales en las que tanto el anión como el catión hidrolizan. Kb para el anión > Ka para el catión, disolución básica Kb para el anión < Ka para el catión, disolución ácida Kb para el anión ≈ Ka para el catión, disolución neutra 15.10 El efecto del ion común es el desplazamiento causado en el equilibrio mediante la adición de un compuesto que tiene un ion común con la sustancia disuelta. La presencia de un ion común suprime la ionización de un ácido o base débil. Considera la mezcla de CH3COONa (electrolito fuerte) y CH3COOH (ácido débil). CH3COONa (s) Na+ (ac) + CH3COO- (ac) CH3COOH (ac) H+ (ac) + CH3COO- (ac) Ion común 16.2 Considera la mezcla de la sal NaA y el ácido débil HA. NaA (s) Na+ (ac) + A- (ac) HA (ac) H+ [H+] -log [H+] (ac) + A- (ac) Ka = Ka [HA] = [A-] = -log Ka - log -log [H+] = -log Ka + log [H+][A-] [HA] Ecuación [HA] [A-] [A-] [HA] [A-] pH = pKa + log [HA] Henderson-Hasselbalch pH = pKa + log [base conjugada] [ácido] pKa = -log Ka 16.2 ¿Cuál es el pH de una disolución que contiene HCOOH 0.30 M y HCOOK 0.52 M? Mezcla de ácido débil y base cojugada! H+ (ac) + HCOO- (ac) HCOOH (ac) Inicial (M) 0.30 0.00 0.52 Cambio (M) -x +x +x x 0.52 + x Equilibrio (M) Efecto ion común 0.30 – x ≈ 0.30 0.52 + x ≈ 0.52 0.30 - x pH = pKa + log [HCOO-] [HCOOH] [0.52] = 4.01 pH = 3.77 + log [0.30] HCOOH pKa = 3.77 16.2 Una disolución reguladora es una disolución de: 1. Un ácido o báse débil y 2. La sal del ácido o base débil 3. Ambos deben estar presentes! Una disolución reguladora es capaz de impedir cambios de pH cuando se añaden pequeñas cantidades de tanto ácido como base. Considera una mezcla equimolar de CH3COOH y CH3COONa Añadimos ácido fuerte: H+ (ac) + CH3COO- (ac) Añadimos base fuerte: OH- (ac) + CH3COOH (ac) CH3COOH (ac) CH3COO- (ac) + H2O (l) 16.3 ¿Cuál de los siguientes es un sistema regulador? (a) KF/HF, (b) KBr/HBr, (c) Na2CO3/NaHCO3 (a) KF es un ácido débil y F- es su base conjugada Disolución reguladora (b) HBr es un ácido fuerte No es disolución reguladora (c) CO32- es una base débil y HCO3- es su ácido conjugado Disolución reguladora 16.3 Calcula el pH del sistema regulador 0.30 M NH3/0.36 M NH4Cl. ¿Cuál es el después de la adición de 20.0 mL de NaOH 0.050 M a 80.0 mL de la disolución reguladora? NH4+ (ac) pH = pKa + log Inicio (moles) final (moles) [NH3] [NH4+] H+ (ac) + NH3 (ac) pKa = 9.25 pH = 9.25 + log [0.30] = 9.17 [0.36] 0.024 0.029 0.001 NH4+ (ac) + OH- (ac) 0.028 0.0 H2O (l) + NH3 (ac) 0.025 volumen final = 80.0 mL + 20.0 mL = 100 mL [NH4 +] 0.028 = [NH3] = 0.10 0.025 0.10 pH = 9.25 + log [0.25] = 9.20 [0.28] 16.3 Manteniendo el pH de la sangre 16.3 Valoraciones En una valoración una disolución de concentración se añade gradualmente a otra disolución de concentración desconocida hasta que la reacción química entre ellas es completa. Punto de equivalencia – el punto en el cual la reacción es completa. Indicador – sustancia que cambia de color en (o cerca) el punto de equivalencia Añadimos base a un ácido desconocido HASTA QUE El indicador Cambia de color (rosa) 4.7 Valoración ácido fuerte-base fuerte NaOH (ac) + HCl (ac) OH- (ac) + H+ (ac) H2O (l) + NaCl (ac) H2O (l) 0.10 M NaOH añadidos a 25 mL de 0.10 M HCl 16.4 Valoración ácido débil-base fuerte CH3COOH (ac) + NaOH (ac) CH3COOH (ac) + OH- (ac) CH3COONa (ac) + H2O (l) CH3COO- (ac) + H2O (l) En el punto de equivalencia (pH > 7): CH3COO- (ac) + H2O (l) OH- (ac) + CH3COOH (ac) 16.4 Valoración ácido fuerte-base débil HCl (ac) + NH3 (ac) NH4Cl (ac) H+ (ac) + NH3 (ac) NH4Cl (ac) En el punto de equivalencia (pH < 7): NH4+ (ac) + H2O (l) NH3 (ac) + H+ (ac) 16.4 Se valoran exactamente 100 mL de HNO2 0.10 M con disolución de NaOH 0.10 M. ¿Cuál es el pH en el punto de equivalencia? inicio (moles) 0.01 0.01 HNO2 (ac) + OH- (ac) 0.0 0.0 NO2- (ac) + H2O (l) final (moles) 0.01 0.01 volumen final = 200 mL = 0.05 M [NO2-] = 0.200 NO2- (ac) + H2O (l) OH- (ac) + HNO2 (ac) Inicial (M) 0.05 0.00 0.00 Cambio (M) -x +x +x x x Equilibrio (M) 0.05 - x [OH-][HNO2] x2 -11 = 2.2 x 10 Kb = = [NO2-] 0.05-x 0.05 – x ≈ 0.05 x ≈ 1.05 x 10-6 = [OH-] pOH = 5.98 pH = 14 – pOH = 8.02 Indicadores Ácido-Base HIn (ac) H+ (ac) + In- (ac) [HIn] ≥ 10 [In ] Color del ácido (HIn) predomina [HIn] ≤ 10 [In ] Color de la base conjugada (In-) predomina 16.5 Curva de valoración de un ácido fuerte con una base fuerte 16.5 ¿Qué indicador(es) usarías en una valoración de HNO2 con KOH ? Ácido débil valorado con base fuerte. En el punto de equivalencia tendremos base conjugada de ácido débil. Punto de equivalencia a pH > 7 Usamos cresol red o phenolphthalein 16.5 pH y Solubilidad • • • La presencia de un ion común disminuye la solubilidad. Bases insolubles se disuelven en disoluciones ácidas. Ácidos insolubles se disuelven en disoluciones básicas. Mg(OH)2 (s) Kps = [Mg2+][OH-]2 = 1.2 x 10-11 Kps = (s)(2s)2 = 4s3 4s3 = 1.2 x 10-11 s = 1.4 x 10-4 M [OH-] = 2s = 2.8 x 10-4 M pOH = 3.55 pH = 10.45 16.9 Mg2+ (ac) + 2OH- (ac) añadimos quitamos A pH menor que 10.45 menor [OH-] OH- (ac) + H+ (ac) H2O (l) Aumenta solubilidad de Mg(OH)2 A pH mayor que 10.45 mayor [OH-] Disminuye solubilidad of Mg(OH)2