Ejercicio 6.2 X1 + X2 + X3 ≥ 4 Producción mínima X1 + 4X2 + 2X3
Anuncio
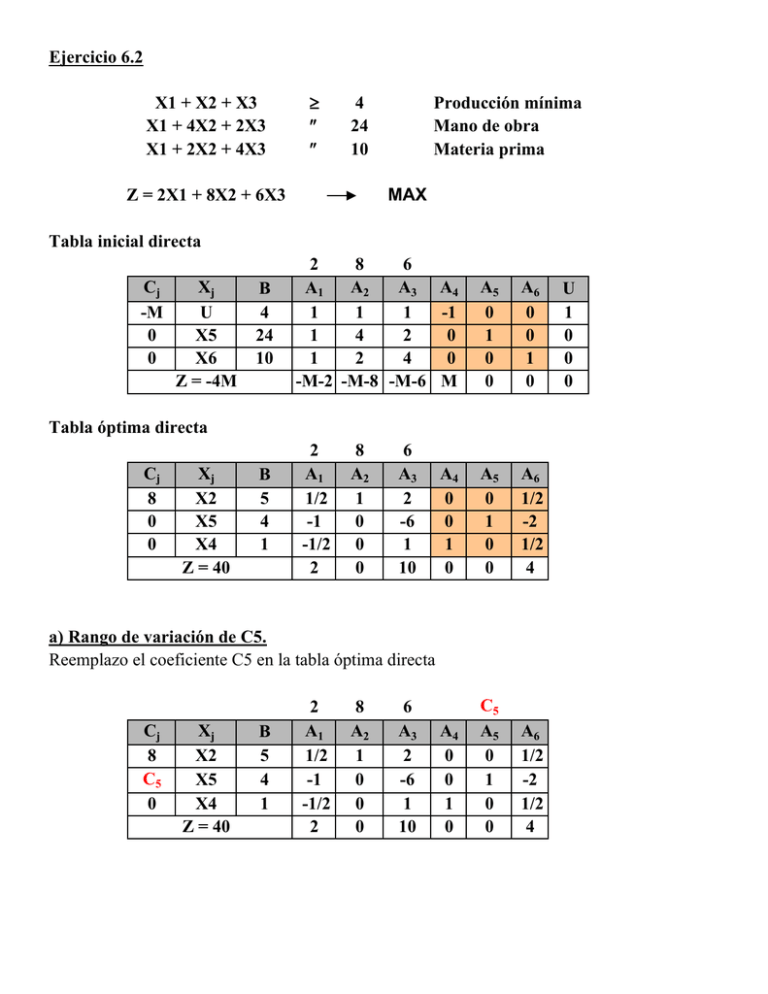
Ejercicio 6.2 X1 + X2 + X3 X1 + 4X2 + 2X3 X1 + 2X2 + 4X3 ≥ ≤ ≤ 4 24 10 Producción mínima Mano de obra Materia prima MAX Z = 2X1 + 8X2 + 6X3 Tabla inicial directa Cj -M 0 0 Xj U X5 X6 Z = -4M B 4 24 10 2 8 6 A2 A3 A4 A1 1 1 1 -1 1 4 2 0 1 2 4 0 -M-2 -M-8 -M-6 M A5 0 1 0 0 A6 0 0 1 0 A4 0 0 1 0 A5 0 1 0 0 A6 1/2 -2 1/2 4 A4 0 0 1 0 C5 A5 0 1 0 0 A6 1/2 -2 1/2 4 Tabla óptima directa Cj 8 0 0 Xj X2 X5 X4 Z = 40 B 5 4 1 2 A1 1/2 -1 -1/2 2 8 A2 1 0 0 0 6 A3 2 -6 1 10 a) Rango de variación de C5. Reemplazo el coeficiente C5 en la tabla óptima directa Cj 8 C5 0 Xj X2 X5 X4 Z = 40 B 5 4 1 2 A1 1/2 -1 -1/2 2 8 A2 1 0 0 0 6 A3 2 -6 1 10 U 1 0 0 0 ≥ ≥ ≥ A1: 8 x 1/2 - C5 - 2 A3: 8 x 2 - 6 C5 - 6 A6: 8 x 1/2 - 2 C5 0 0 0 ⇒ ⇒ ⇒ C5 C5 C5 ≤ ≤ ≤ C5 ≤ 5/3 2 5/3 2 b) Utilidad unitaria mínima de P7. Dado que se trata de un nuevo producto, el análisis se realiza sobre la tabla directa [A-1]= 0 0 -1 Cj 8 0 0 0 1 0 Xj X2 X5 X4 Z = 40 1/2 -2 1/2 B 5 4 1 x 0 4 3 = 2 A1 0,5 -1 -0,5 2 8 A2 1 0 0 0 6 A3 2 -6 1 10 3/2 -2 3/2 A4 0 0 1 0 A5 0 1 0 0 C7 A6 A7 0,5 1,5 -2 -2 0,5 1,5 4 ≤0 Para que sea conveniente producirlo, el Zj - Cj del P7 debe ser negativo y así ingresar en la base. 8 x 3/2 + 0x(-2) + 0 x 3/2 - C7 ≤0 ⇒ C7 ≥ 12 c) Gráficos: X2, Y2, Z en función de b3 Analizo cuál es el rango de validez de la Tabla Optima Dual Cj b3 0 0 Yj Y3 Y4 Y6 Z = 40 B 4 2 10 -4 A1 -1/2 1/2 -1 -1 24 A2 2 1 6 -4 b3 A3 1 0 0 0 A4 A5 A6 0 -1/2 0 1 -1/2 0 0 -2 1 0 -5 0 A1: (-1/2) b3 +4 A2: 2 b3 - 24 A6: (-1/2) b3 ≤ ≤ ≤ 0 0 0 ⇒ ⇒ ⇒ b3 b3 b3 ≥ ≤ ≥ 8 12 0 8 ≤ b3 ≤ 12 (-1/2) b3 = - X2 ⇒ Z = 4 b3 Y2 = 0 ; X2 = 1/2 b3 Tomo b3=8 Cj 8 0 0 Cj b3 -4 0 A2: 3b3 -8 -24 A4: b3 - 8 A5: - b3 + 4 B 4 2 10 -4 A1 -1/2 1/2 -1 0* 24 A2 2 1 6 -8 8 A3 1 0 0 0 A4 A5 A6 0 -1/2 0 1 -1/2 0 0 -2 1 0 -4 0 Yj Y3 Y1 Y6 Z = 32 B 6 4 14 -4 A1 0 1 0 0 24 A2 3 2 8 -8 b3 A3 1 0 0 0 A4 1 2 2 0* ≤ ≤ ≤ 0 0 0 ⇒ ⇒ ⇒ b3 b3 b3 ≤ ≤ ≥ 32/3 8 4 4 ≤ b3 ≤ 8 Yj Y3 Y4 Y6 Z = 32 Z = 6 b3 - 16 A5 -1 -1 -3 -4 A6 0 0 1 0 θ 4 - Y2 = 0 ; - b3 + 4 = - X2 ⇒ X2 = b3 - 4 Tomo b3= 12 B 4 2 10 -4 A1 -1/2 1/2 -1 -2 24 A2 2 1 6 0* 12 A3 1 0 0 0 A4 A5 A6 0 -1/2 0 1 -1/2 0 0 -2 1 0 -6 0 Yj Y3 Y4 Y2 Z = 48 B 2/3 1/3 5/3 -4 A1 -1/6 2/3 -1/6 -2 24 A2 0 0 1 0 b3 A3 1 0 0 0 A4 A5 A6 0 1/6 -1/3 1 -1/6 -1/6 0 -1/3 1/6 0 -6 0* ≤ ≤ ≤ 0 0 0 ⇒ ⇒ ⇒ b3 b3 b3 ≥ ≤ ≥ 0 48 12 12 ≤ b3 ≤ 48 Yj Y3 Y4 Y6 Z = 48 Cj 12 0 0 Cj b3 0 24 A1: (-1/6) b3 -4+4 A5: 1/6 b3 - 8 A6: 4 - 1/3 b3 θ 2 2 5/3 Z = 40 + 2/3 b3 Y2 = 5/3 ; - 8 + 1/6b3 = - X2 ⇒ X2 = - 1/6b3+ 8 X2 = f (b3) 10 9 8 7 4 0 6 2 8 4 9 4,5 10 12 18 24 48 5 6 5 4 0 X2 6 5 4 3 2 1 0 0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40 42 44 46 48 50 b3 4 8 12 12 20 48 10 0 0 0 1,6667Y2 = f (b3) 1,6667 1,6667 9 8 7 Y2 6 5 4 3 2 1 0 0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40 42 44 46 48 b3 4 8 Z 6 8 10 12 30 48 80 76 72 68 64 60 56 52 48 44 40 36 32 28 24 20 16 12 8 4 0 0 2 4 6 8 20 32 40 48 60 72 Z = f (b3) 10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40 42 44 46 48 b3 d) Incorporación de un nuevo proceso. -1 Se analiza sobre las tablas duales. Multiplico la matriz [A ] por el vector con los nuevos coeficientes Tabla inicial dual Cj -M -M -M Yj U1 U2 U3 Z= -16M B 2 8 6 -4 A1 -1 -1 -1 24 A2 1 4 2 10 A3 1 2 4 3M-4 -6M-24 -7M-10 A4 -1 0 0 M A5 0 -1 0 M A6 0 0 -1 M Tabla óptima dual [A-1]= Cj 10 0 0 Yj Y3 Y4 Y6 Z = 40 B 4 2 10 0 -1 0 1/2 1/2 2 0 0 -1 A1 -1/2 1/2 -1 -1 A2 2 1 6 -4 x 4 2 3 A3 1 0 0 0 = A4 A5 A6 0 -1/2 0 1 -1/2 0 0 -2 1 0 -5 0 1 -3 1 Zj-Cj = 10 x 1 - 0 x (-3) + 1 x 0 - 11 = -1 Zj-Cj ≤ 0 ⇒ no altera la tabla óptima M U1 1 0 0 0 M U2 0 1 0 0 M U3 0 0 1 0 e) Valor del recurso MP (4 kg por semana) 4 5 6 7 8 8 10 11 12 8 7 y3 ($/kg) 6 5 4 3 6 6 6 6 6 4 4 4 4 12 0,67 y3 20 = f(b 0,673) 48 0,67 2 1 0 0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40 42 44 46 48 50 b3 (kg) f) Curva de oferta del producto B para C2 entre 0 y 100 Analizo el rango de validez de la tabla óptima directa según C2 Cj C2 0 0 A1: 1/2 x C2 - 2 A3: 2 C2 - 6 A6: 1/2 x C2 Xj X2 X5 X4 Z = 40 B 5 4 1 2 A1 1/2 -1 -1/2 2 ≥ ≥ ≥ 0 0 0 ⇒ ⇒ ⇒ C2 A2 1 0 0 0 6 A3 2 -6 1 10 A4 0 0 1 0 C2 C2 ≥ ≥ ≥ 4 3 0 C2 A5 0 1 0 0 A6 1/2 -2 1/2 4 C2 ≥ 4 Ingreso C2 = 4 Xj X2 X5 X4 Z = 20 Cj 4 0 0 2 A1 1/2 -1 -1/2 0* B 5 4 1 4 A2 1 0 0 0 6 A3 2 -6 1 2 A4 0 0 1 0 A5 0 1 0 0 A6 θ 1/2 10 -2 1/2 2 Al entrar X1 y salir X2, sabemos que X2 valdrá cero para todo valor de C2 entre 0 y 4 0 x2 (u) 2 0 x2 0= f(c2) 4 0 6 4 5 5 20 5 4 100 5 3 2 1 0 0 5 10 15 20 25 30 35 40 45 50 55 c2 ($/u) 60 65 70 75 80 85 90 95 100 105




