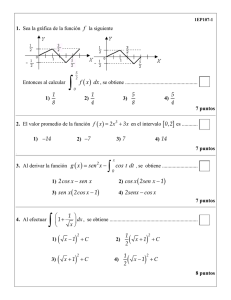
CÀLCUL
Anuncio

CÀLCUL
Grau en Enginyeria de la Construcció, Curs 2010-2011
TG3: Extremos de varias variables
Problema 1. Hallar y clasificar los puntos críticos de la función f (x, y) = sen(x) cosh(y)
Solución: Como la función es diferenciable por ser producto de un seno y un coseno hiperbólico podemos aplicar las condiciones necesarias y suficientes de extremo libre. Tendremos
en cuenta que cosh(y) 6= 0, que senh(y) = 0 sii y = 0 y que cos(x) y sen(y) no se anulan
simultáneamente.
Condición necesaria:
∂f
= cos(x) cosh(y) = 0
∂x
∂f
= sen(x)senh(y) = 0
∂y
π
para todo k ∈ Z.
2
De la segunda ecuación tenemos entonces que necesariamente senh(y) = 0; es decir, y = 0.
Por tanto los puntos estacionarios son los de la forma
De la primera ecuación tenemos que cos(x) = 0, es decir, x = (2k + 1)
π (2k + 1) , 0 para todo k ∈ Z.
2
Por otro lado,
Hf (x, y) =
−sen(x) cosh(y) cos(x)senh(y)
cos(x)senh(y) sen(x) cosh(y)
Por lo que,
π (−1)k+1
0
Hf (2k + 1) , 0 =
0
(−1)k
2
−→ ∆1 = (−1)k+1 , ∆2 = (−1)k+1 (−1)k = (−1)2k+1 = −1 < 0.
En definitiva,
1
2
π Todos los puntos de la forma (2k + 1) , 0 son puntos de silla o inflexión.
2
Problema 2. Hallar los valores máximo y mínimo de la funión f (x, y) = x2 + 14 y 2 − xy en
2
el conjunto Q = {(x, y) : x ≤ 0, y ≤ 0, x2 + y4 ≤ 1}.
Solución: Nótese que f es una función continua (es una función polinómica) y Q es un
conjunto compacto. Por tanto, el Teorema de Weierstrass asegura la existencia de extremos
absolutos, que se encontrarán entre los puntos siguientes:
(i) Extremos libre de f en el interior de Q:
Como estamos bajo hipótesis de diferenciabilidad podemos aplicar la condición necesaria
de extremo libre
∂f
= 2x − y = 0
◦
∂x
=⇒ (x, 2x) ∈Q, si − 1 < x < 0.
∂f
1
= y−x=0
∂y
2
(ii) Extremos condicionados en la frontera de Q.
(ii.1) Frontera x2 +
y2
4
= 1. Debemos aplicar la regla de los multipliadores de Lagrange:
1
y2
L(x, y, z, λ) = x2 + y 2 − xy + λ(x2 +
− 1).
4
4
La condición necesaria de extremos condicionada nos proporciona el siguiente sistema:
∂L
= 2x − y + 2λx = 2x(1 + λ) − y = 0
∂x
∂L
1
1
y
= y − x + λy = (1 + λ) − x = 0 ,
∂y
2
2
2
2
y
2
=1
x +
4
de las dos primeras ecuaciones tenemos que si x, y 6= 0
2x
y
= (1 + λ) =
−→ 4x2 = y 2 .
2x
y
c Càlcul, E. Construcció. etseccpb, 2010-11
3
Sustituyendo en la última ecuación tenemos que,
1
x = ±√ .
2
Si x = 0, de la primera y = 0, lo que es imposible
ocurre si y = 0. En definitiva,
y lo mismo
√ 1
los candidatos a extremo en esta frontera son − √2 , − 2 .
(ii.1) Frontera x = 0, y < 0. Al tratarse de una ecuación despejada podemos sustituir
directamente la condición en la función f .
h(y) = f (x = 0, y) = 41 y 2
Aplicamos la condición necesario de extremo libre y obtenemos que:
h′ (y) = 21 y = 0 −→ y = 0.
Por lo que no tenemos ningún candidato a extremo en está región.
noindent (ii.1) Frontera y = 0, x < 0. Al tratarse de una ecuación despejada podemos
sustituir directamente la condición en la función f .
k(x) = f (x, y = 0) = x2
Aplicamos la condición necesario de extremo libre y obtenemos que:
k ′ (x) = 2x = 0 −→ x = 0.
Por lo que no tenemos ningún candidato a extremo en está región.
(iii) Por último debemos considerar los vértices del conjunto, es decir, los puntos que
se obtiene como intersección de dos de las curvas frontera. En este caso, (0, −2), (−1, 0) y
(0, 0).
Para finalizar basta valorar la función en los puntos obtenidos:
c Càlcul, E. Construcció. etseccpb, 2010-11
4
(x, y)
f (x, y)
(x, 2x)
0
mínimo absoluto
√
(− √12 , − 2)
0
mínimo absoluto
(0, 0)
0
mínimo absoluto
(0, −2)
1
máximo absoluto
(−1, 0)
1
máximo absoluto
c Càlcul, E. Construcció. etseccpb, 2010-11