Encuentre , , y y sus dominios: Encuentre las funciones, y sus
Anuncio

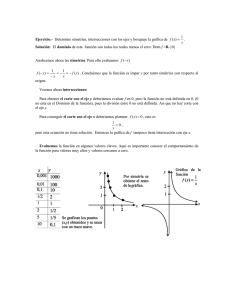
1. Encuentre 𝑓 + 𝑔, 𝑓 − 𝑔, 𝑓𝑔 y 𝑓/𝑔 y sus dominios: f ( x) 4 x 2 , g ( x) 1 x 2. Encuentre las funciones, 𝑓 𝑜 𝑔, 𝑔 𝑜 𝑓, 𝑓 𝑜 𝑓 𝑦 𝑔 𝑜 𝑔 y sus dominios f ( x) x , x 1 g ( x) 2 x 1 3. Cuota de servicio: Por sus servicios, un investigador privado requiere una cuota de retención de S/ 500 más S/ 80 por hora. Sea x el número de horas que el investigador pasa trabajando en un caso. (3p) a) Halle una función f que modela la cuota del investigador como una función de x. b) Encuentre 𝑓 −1 . ¿Qué representa 𝑓 −1 ? c) Encuentre 𝑓 −1 (1220) ¿Qué representa su respuesta? 4. Bosqueje la gráfica de la función polinomial. Asegúrese de que su gráfica muestre las intersecciones con los ejes y exhiba el comportamiento extremo apropiado. (2p) P( x) (2 x 1)(x 1)(x 3) 5. Encuentre las intersecciones y asíntotas, y luego bosqueje una gráfica de la función racional. f ( x) x 2 3x x2 x 6 6. Crecimiento poblacional: Suponga que la población de conejos de la granja del señor Ruiz sigue la formula: p (t ) 3000 t t 1 Donde 𝑡 ≥ 0 es el tiempo (en meses) desde el comienzo del año. a) Trace una gráfica de la población de conejos b) ¿Qué sucede finalmente con la población de conejos? 7. Encuentre la función exponencial 𝑓(𝑥) = 𝑎 𝑥 cuya gráfica se muestra. a) b) 8. Población de aves. La población de cierta especie de ave está limitada por el tipo de hábitat requerido para anidar. La población se comporta de acuerdo con el modelo de crecimiento logístico: n(t ) 5600 0.5 27.5e 0.044t donde t se mide en años a) Encuentre la población inicial de aves b) Dibuje la gráfica de la función 𝑛(𝑡) c) ¿Qué tamaño tiene la población cuando el tiempo avanza?