5. celosías i

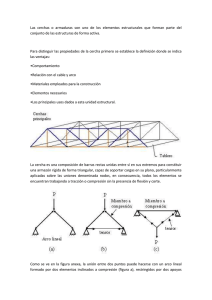
SKILLS%Project%%
DISEÑO%DETALLADO%DE%CELOSÍAS%–%PARTE%1%
%
OBJETIVOS%DE%APRENDIZAJE%
!  Consejos%sobre%el%cálculo%de%celosías%para%edificios%
de%una%sola%planta%
!
!  Guía%de%diseño:%
Análisis%global%
"  Comprobación%de%elementos%
"  Comprobación%de%uniones%
!
" 
3"
ÍNDICE%
!  Introducción%
!  Diseño%de%detalle%
!  Cálculo%
Predimensionamiento!
"  Análisis!global%
!  Comprobación%de%elementos%
"  Comprobación!de!elem.!some7dos!a!compresión!(y!flexión)!
"  Comprobación!de!elem.!some7dos!a!tracción!(y!flexión)!
!  Comprobación%de%uniones%
"  Uniones!atornilladas!
"  Uniones!soldadas!
!  Conclusión%
" 
4"
%
INTRODUCCIÓN%
INTRODUCCIÓN%
!  Definición:!!
"  Una!
celosía! es,! básicamente,! un! sistema! triangulado!
compuesto! por! elementos! estructurales! (normalmente)!
rectos!interconectados.!
"  Los! elementos! individuales! se! interconectan! en! los! nudos;!
que!se!suelen!considerar!uniones!nominalmente!ar7culadas.!
"  Las!fuerzas!externas!aplicadas!al!sistema!y!las!reacciones!en!
los!soportes!se!aplican!por!regla!general!en!los!nudos.!
"  Cuando! todos! los! elementos! y! fuerzas! aplicadas! se!
6"
encuentren!en!el!mismo!plano,!se!trata!de!una!celosía!en!2D.!
INTRODUCCIÓN%
!  El!esfuerzo!principal!sobre!cada!elemento!es!tracción!o!compresión!
axil.!
1!L!Esfuerzo!axil!de!compresión!
2!L!Esfuerzo!axil!de!tracción!
Elementos!some7dos!a!fuerzas!axiles!en!una!celosía!simple!!
!  Cuando! las! uniones! de! los! nudos! son! rígidas,! se! introduce! una!
flexión!secundaria,!que!se!trata!más!adelante.!
7"
INTRODUCCIÓN%
Empleo%de%celosías%en%edificios%de%una%sola%planta%
%
!  Para!soportar!la!carga!de!la!cubierta:!!
"  Cargas! gravitatorias! (peso! propio,! cubierta! y! equipamiento,!
bien! sobre! la! cubierta,! bien! suspendido! de! la! estructura,!
cargas!de!nieve);!
"  Acciones!ocasionadas!por!el!viento!(incluida!la!succión).!
!
!  Para!aportar!estabilidad!horizontal:!!
"  Vigas!contraviento!a!nivel!de!cubierta,!o!a!niveles!intermedios!
si!fuera!necesario;!
"  Arriostramiento! ver7cal! en! los! muros! laterales! y/o! en! los!
testeros.!
8"
INTRODUCCIÓN%
Tipos%de%disposición%general%
de%la%estructura%de%un%edificio%
Qpico%de%una%sola%planta%
%
%
Disposición%del%pórRco%
! Estabilidad!lateral!aportada!por!celosías!de!pór7co;!
! Estabilidad!longitudinal!aportada!por!el!contraviento!transversal!y!
cruces!de!San!Andrés!(en!azul);!
! No!existe!ningún!contraviento!longitudinal.!
9"
INTRODUCCIÓN%
Tipos%de%disposición%general%de%la%
estructura%de%un%edificio%Qpico%de%
una%sola%planta%
%
%
Disposición%de%vigas%y%pilares%
! Celosías!ver7cales!simplemente!apoyadas!sobre!los!pilares;!
! Estabilidad!lateral!aportada!por!el!contraviento!longitudinal!y!los!
arriostramientos!ver7cales!en!los!testeros!(en!azul);!
! Estabilidad!longitudinal!aportada!por!el!contraviento!transversal!y!
los!arriostramientos!(en!verde).!10"
INTRODUCCIÓN%
Tipos%de%disposición%general%de%la%
estructura%de%un%edificio%Qpico%de%
una%sola%planta%
%
%
Disposición%en%“dientes%de%sierra%”%
! Las!celosías!principales!se!representan!en!
azul:!su!luz!(L)!es!la!parte!larga!de!la!malla!
de!pilares.!
! Las!celosías!secundarias!(en!verde)!7enen!
una!luz!más!corta!A!(distancia!entre!las!
celosías!principales).!
! En!rojo!se!muestran!los!elementos!que!
sujetan!las!ventanas!de!orientación!norte.!
11"
INTRODUCCIÓN%
Diferentes%Rpos%de%celosías%%
En! una! celosía! Rpo% %PraX,! las! diagonales! están!
some7das! a! tracción! bajo! cargas! gravitatorias.! Se!
u 7 l i z a n! c u a n d o! p r e d o m i n a n! l a s! c a r g a s!
gravitatorias.!
En! la! celosía! de! la! imagen! las! diagonales! están!
s o m e 7 d a s! a! t r a c c i ó n! b a j o! c a r g a s! d e!
levantamiento.!Se!u7lizan!cuando!predominan!las!
cargas!de!levantamiento,!como!edificios!abiertos.!
En! una! celosía! Rpo% Warren,! las! diagonales! se!
encuentran! de! modo! alterna7vo! a! tracción! y! a!
compresión.! Se! suelen! u7lizar! como! vigas!
horizontales!en!puentes!grúa.!
Todos! los! 7pos! de! celosías! pueden! u7lizarse! bién! en! estructuras!
de! celosía! de! pór7co! o! en! estructuras! de! celosías! simples! de!!
grandes!luces,!que!van!desde!20!hasta!100m.!
12"
INTRODUCCIÓN%
%
Diferentes%Rpos%de%celosías%(conRnuación)%
%
Existen!dos!7pos!de!celosía!en%cruz:!
%
!  Si!las!diagonales!han!sido!calculadas!para!resis7r!la!
compresión,! la! celosía! en! cruz! es! la! superposición!
de!dos!celosías!7po!Warren.!
!  Si! se! ignora! la! resistencia! de! los! elementos!
diagonales!a!compresión,!el!comportamiento!será!el!
mismo!que!en!una!celosía!7po!PraY.!
Se! u7liza! con! frecuencia! en! contravientos,! en! los! que!
las!diagonales!son!muy!largas.!
Se!pueden!añadir!elementos!secundarios!para:!
!  crear!puntos!de!carga!intermedios;!
!  limitar! la! longitud! de! pandeo! de! los! elementos! a!
compresión! (sin! influir! en! el! comportamiento!
estructural!global).!
Para! cualquiera! de! los! 7pos! que! se! han! descrito,! es!
posible!diseñar!el!cordón!superior!en!pendiente!(a!una!
o! dos! aguas)! para! soportar! la! cubierta.! El! ejemplo!
muestra!una!celosía!a!dos!aguas.!
13"
INTRODUCCIÓN%
%
Diferentes%Rpos%de%celosías%(conRnuación)%
% pendiente! única! para! estas!
Cordón! superior! de!
celosías! triangulares,! que! forman! parte! de! una!
cubierta! en! "diente! de! sierra".! Ventanas! con!
orientación!norte.!
Celosía!Fink:!
Este! 7po! de! celosía! se! u7liza! más! comúnmente!
en! las! cubiertas! de! viviendas! y! luces! pequeñas!
(entre!10!y!15!m)!
!
Este!7po!de!celosía!se!puede!u7lizar!para!luces!
mayores.!
Estas!celosías!pueden!ser!simplemente!apoyadas!
14"
DISEÑO%DE%DETALLE%
DISEÑO%DE%DETALLE%
Geometría%general%de%celosías%para%estructuras%de%cubierta!
!  Las! celosías! suelen! suponer! una! solución! económica! para! grandes!
luces,!a!par7r!de!20!ó!25!m.;!
!  Para! conseguir! un! buen! rendimiento! estructural,! habrá! que! optar!
por!una!relación!entre!la!luz!y!el!canto!de!la!celosía!de!10!a!15;!
!  La!
inclinación! de! los! elementos! diagonales,! en! relación! a! los!
cordones,!deberá!ser!de!entre!35o!y!55o;!
!  Sólo!se!aplicarán!cargas!puntuales!en!los!nudos;!
!  La! orientación! de! los! elementos! diagonales! deberá! ser! tal! que! los!
elementos!más!largos!estén!some7dos!a!tracción!(estando!los!más!
cortos!some7dos!a!compresión).!
16"
DISEÑO%DE%DETALLE%
%
Sección%de%los%elementos%
!  Las!secciones!deberían!ser!simétricas!para!la!flexión!fuera!del!plano!
ver7cal!de!la!celosía;!
!  En!los!elementos!some7dos!a!compresión,!la!resistencia!al!pandeo!
en!el!plano!ver7cal!de!la!celosía!deberá!será!similar!a!la!resistencia!
al!pandeo!fuera!del!plano;!
!  Para! elementos! some7dos! a! grandes! fuerzas! una! buena! solución!
sería:!
" 
Cordones! con! secciones! IPE,! HEA! o! HEB,! o! con! una! sección!
compuesta!de!dos!perfiles!en!U!(UPE);!
" 
Elementos! diagonales! formados! por! dos! angulares!
empresillados.!
17"
DISEÑO%DE%DETALLE%
Tipo%de%uniones%
Uniones%de%
celosía%
Empalmes%
prefabricada!
soldada!
atornillada!
directa!al!
cordón!
a!través!de!
cartelas!
uniones!in!situ!
atornillada!
con!
cubrejuntas!
18"
con!placas!de!
extremo!
DISEÑO%DE%DETALLE%
ConRnuidad%de%los%cordones%
!  El! diseño! de! dichas! uniones! atornilladas! depende! del! 7po! de!
sección!del!cordón!que!se!pretende!unir.!
!  Se!pueden!dis7nguir!dos!7pos!de!uniones!atornilladas:!
con%placas%de%extremo%
con%cubrejuntas%
!
%
!
!
!  Cuando!los!cordones!están!compuestos!por!:!
"  un! único! perfil/sección! en! I! o! H,! se! pueden! u7lizar! cualquiera!
de!las!uniones!mencionadas;!
"  dos! angulares! dobles! o! perfiles! en! “U”,! normalmente! es!
preferible!u7lizar!cubrejuntas;!
"  perfiles! tubulares! es! preferible! u7lizar! uniones! con! placas! de!
extremo.!!
19"
DISEÑO%DE%DETALLE%
Unión%de%las%diagonales%con%los%cordones%
!  Cuando! los! cordones! están! compuestos! por!
elementos!dobles!(dos!angulares!o!dos!secciones!
UPE),! es! habitual! insertar! cartelas! entre! los! dos!
elementos!que!componen!el!cordón.!Las!cartelas!
están!soldadas!o!atornilladas!a!los!cordones.!Las!
diagonales! y! los! montantes! son! normalmente!
atornillados!a!las!cartelas.!
!
!  Cuando!
los! cordones! están! compuestos! por!
perfiles! IPE! o! HEA/HEB! el! método! habitual! es!
u7lizar!igualmente!una!cartela!soldada!al!cordón.!
La! cartela! va! unida! al! ala! cuando! el! perfil! está!
posicionado! con! el! alma! ver7cal,! y! al! alma!
cuando! el! perfil! está! posicionado! con! el! alma!
horizontal.!
20"
%
DISEÑO%DE%DETALLE%
%
Estabilidad%del%pórRco%
!  El! arriostramiento! en! dos! direcciones! perpendiculares! proporciona!
la! estabilidad! en! el! plano,! y! la! celosía! está! simplemente! apoyada!
sobre!los!pilares;!
!  Para!permi7r!dicha!rotación!global!es!necesario!tener!en!cuenta!el!
desplazamiento! horizontal,! en! el! extremo! de! uno! de! los! cordones!
respecto!al!montante:!normalmente,!el!desplazamiento!del!cordón,!
que!no!está!unido!al!elemento!dispuesto!en!diagonal!en!el!soporte,!
está!liberado.!
!
!  En!
la! dirección! longitudinal! la! estabilidad! se! consigue! con!
21"
arriostramientos!ver7cales!
DISEÑO%DE%DETALLE%
Estabilidad%lateral%
!
Celosía!
!  Línea% de% trazos% en% negro:! dos! celosías!
consecu7vas!
!
!  En! azul:! La! correa! que! completa! el!
!
arriostramiento!en!la!región!superior!
!
!  En!verde:!El!elemento!longitudinal!que!
cierra! el! arriostramiento! en! la! parte!
!
inferior!
Arriostramiento! con! cruces! de!
!  En! rojo:! Arriostramiento! ver7cal! de! la!
22"
San!Andrés!entre!las!celosías!
cubierta!
!
!
DISEÑO%DE%DETALLE%
%
Estabilidad%lateral%
!  Las! correas! (y! el! contraviento! transversal! de! la! cubierta)!
normalmente! proporcionan! la! estabilidad! lateral! de! los! cordones!
superiores!de!celosías,!pero!donde!esté!permi7do!el!uso!de!paneles!
resistentes! a! cortante,! se! podrá! conseguir! la! estabilidad! sin!
arriostramientos.!
!
Paneles!de!cubierta!actuando!como!paneles!resistentes!cortante!en!
una!celosía!de!cubierta!rigidizada!
23"
CÁLCULO%
CÁLCULO%–%GENERAL%%
Información%
%contractual%
•  Datos%geométricos%
•  Incidencia%deconstrucciones%%
vecinas%
•  Obligaciones%o%restricciones%%
en%los%elementos%de%los%
cordones%
•  Naturaleza%y%posición%de%
las%cargas%permanentes%
•  Naturaleza%y%posición%de%la%
sobrecarga%de%uso%
•  Función%estabilizadora%de%
la%envolvente%(diafragma)%
INFORMACIÓN%
ELECCIÓN%DE%
ANÁLISIS%GLOBAL%
CRITERIOS%DE%
VERIFICACIÓN%
DE%ELS%
Diagrama!de!flujo!
para!el!cálculo!de!
elementos!
estructurales!
EN%1993d1d1%
EN%1993d1d8%
25"
VERIFICACIÓN%DE%LA%
RESISTENCIA%DE%LOS%
ELEMENTOS%
VERIFICACIÓN%DE%LA%
RESISTENCIA%DE%
LAS%UNIONES%
Información%
reglamentaria%y%
normaRva%
•  Acciones%climáRcas%%
•  Acciones%sísmicas%
•  Acciones%de%
explotación%
•  ...%
CÁLCULO%–%PREDIMENSIONAMIENTO%
Pasos%a%seguir%en%el%diseño%
!  Cálculo!de!las!cargas!sobre!la!celosía;!
!  Definición!
del! ancho! de! la! celosía! y! de! la! distribución! de!
diagonales!y!montantes;!!
!  Cálculo!de!los!esfuerzos!en!los!cordones,!diagonales!y!montantes!
suponiendo! uniones! ar7culadas! (mediante! socware! o! métodos!
simplificados);!
!  Selección!del!cordón!comprimido;!
!  Selección!del!cordón!traccionado;!
!  Selección!de!diagonales!y!montantes,!asegurando!una!fácil!unión;!
!  Comprobación!de!flechas.!
26"
CÁLCULO%–%PREDIMENSIONAMIENTO%
%
Cálculo%de%esfuerzos%en%celosías%
arRculadas%en%sus%extremos%
Métodos!simplicados!manuales%
%
!  Equilibrio!de!fuerzas!en!los!nudos!
!  Tomando!momentos!sobre!el!nudo!D!se!
calcula!el!esfuerzo!en!el!elemento!CB!
27"
CÁLCULO%–%PREDIMENSIONAMIENTO%
Selección%del%%perfil%del%cordón%comprimido%
! 
La! longitud! de! pandeo! en! el! plano! es! igual! a! la! longitud! entre!
nudos;!!
! 
La!longitud!de!pandeo!fuera!del!plano!es!igual!a!longitud!entre!
coacciones!del!cordón!(!definida!normalmente!por!la!separación!
entre!correas)!
!
Selección%del%%perfil%del%cordón%traccionado%
!
! 
El! caso! más! crí7co! suele! ser! el! de! levantamiento! (succión)! lo!
que!provoca!que!el!cordón!esté!comprimido;!!
! 
El! pandeo! fuera! del! plano! es! el! más! crí7co,! y! por! ello! se! suele!
coaccionar! su! longitud! de! pandeo! con! algún! 7po! de!
arriostramiento.!
28"
CÁLCULO%–%ANÁLISIS%GLOBAL%
!  En! la! realidad,! las! estructuras! se! desvían! de! su! comportamiento!
teórico,! y! su! análisis! global! debe! tener! en! cuenta! dichas!
desviaciones.!
!  ! En! par7cular,! dichas! desviaciones! incluyen! la! flexión! de! los!
elementos,! además! de! los! esfuerzos! axiles.! Dichos! momentos!
flectores,! conocidos! como! “momentos! secundarios”,! pueden!
ocasionar! tracciones! adicionales! significa7vas! en! los! elementos!
que!componen!la!celosía.!
!  Las!desviaciones!en!el!diseño!se!presentan!de!diferentes!formas:!
"  Los! elementos! que! componen! la! estructura! no! suelen! estar!
ar7culados!en!sus!nodos.!
"  Los!elementos!no!siempre!están!adecuadamente!alineados!con!
los!nodos!en!los!que!se!conectan.!!
"  Las!cargas!no!siempre!se!aplican!de!forma!estricta!a!los!nudos.!
29"
CÁLCULO%–%ANÁLISIS%GLOBAL%
Modelización%de%una%celosía%
%
!  Una!
celosía! puede! igualmente! ser! modelizada! sin! sus! pilares!
cuando!esté!ar7culada!a!los!mismos;!
!
!  Al!u7lizar!modelos!independientes,!y!para!la!comprobación!de!la!
resistencia!de!determinados!elementos,!puede!resultar!necesario!
combinar! los! resultados! de! diversos! análisis,! por! ejemplo:! el!
cordón! superior! de! una! celosía! es! igualmente! u7lizado! como!
cordón!de!la!viga!contraviento.!
!
!  Si!se!u7liza!un!modelo!global!en!3D,!se!puede!observar!una!flexión!
"parásita",! que! crea! una! precisión! ilusoria! del! comportamiento!
estructural.! Es! por! este! mo7vo! que! suelen! ser! preferibles! los!
modelos!en!2D.!
30"
CÁLCULO%–%ANÁLISIS%GLOBAL%
%
Modelización%de%una%celosía%
!
Las!celosías!se!representan!mediante!una!de!las!dos!opciones!que!
se!indican:!
!  Cordones%conRnuos%(y,!por!lo!tanto,!los!elementos!que!forman!
los! cordones! están! conectados! de! forma! rígida! en! ambos!
extremos)!
!  Elementos% de% la% celosía% (dispuestos! en! diagonal! y! en! ver7cal)!
unidos!mediante!ar7culaciones!a!los!cordones.!
!
31"
CÁLCULO%–%ANÁLISIS%GLOBAL%
Análisis%global%simplificado
!  Una! viga! triangulada! con! una! profundidad! constante! se! puede!
equipararse! a! una! viga! en! doble! T.! Esta! equivalencia! es! posible! y!
permite! una! buena! aproximación,! por! ejemplo,! para! una! celosía!
con!cordones!paralelos.!
!  El!esfuerzo!cortante!global!Vglobal!y!el!momento!flector!global!Mglobal!
de!la!viga!equivalente!varían!muy!poco!a!lo!largo!de!un!panel,!y!se!
pueden!igualar!a!los!valores!medios!del!panel.!Por!lo!tanto,!la!carga!
axil!puede!evaluarse!u7lizando!las!siguientes!expresiones:!
"  En!los!cordones!
Nch = ±Mglobal / h
!
"  En!una!diagonal!
!
Nd = ±Vglobal / cosθ
32"
CÁLCULO%–%ANÁLISIS%GLOBAL%
Análisis%global%simplificado
!
!
!  También!se!puede!hacer!una!es7mación!de!la!flecha!de!la!celosía,!
calculando! la! de! una! viga! equivalente! con! la! misma! carga.! Para!
ello,! se! puede! u7lizar! teoría! de! vigas,! aplicando! a! la! viga!
equivalente!un!momento!de!inercia!igual!a:!
2
I = ∑ Ach,i × di2
donde:!
i=1
Ach,i!–!es!la!sección!del!cordón!i!
di!–!es!la!distancia!desde!el!centro!de!gravedad!de!los!dos!cordones!
al!centro!de!gravedad!del!cordón!i.!
!  Para! poder! tener! en! cuenta! las! deformaciones! globales! por!
cortante,!que!no!se!tratan!con!las!fórmulas!elementales,!se!u7liza!
un!módulo!de!elas7cidad!reducido.!
33"
CÁLCULO%–%ANÁLISIS%GLOBAL%
Esfuerzos%secundarios%
Hay!momentos!flectores!y!esfuerzos!cortantes!debidos!a:!
!  !influencia!de!la!rigidez!de!los!cordones!
!  suposición!de!uniones!rígidas!en!la!celosía!
!que!deben!sumarse!a!parte!de!los!esfuerzos!axiles!originales!
(calculados! bajo! la! suposición! de! que! los! nudos! están!
ar7culados)!
!
Durante! el! proceso! de! diseño! es! habitual! u7lizar! cordones!
con7nuos!y!ar7cular!los!elementos!de!la!celosía.!
!
34"
CÁLCULO%–%ANÁLISIS%GLOBAL%
Influencia%de%los%efectos%secundarios%
!  La! transformación! de! las! uniones! ar7culadas! en! nudos! rígidos! no!
suele! conllevar! una! variación! de! los! esfuerzos! axiles! en! los!
elementos;!
!  La! flexión! del! elemento! debido! a! momentos! flectores! secundarios!
sólo!ocasiona!una!ligera!variación!en!la!distancia!entre!los!extremos!
de! este! elemento! en! comparación! con! la! diferencia! de! longitud!
debida!al!esfuerzo!axil.!
!  Cuanto!
mayor! sea! la! rigidez! de! los! cordones! (normalmente! son!
con7nuos),! en! comparación! con! la! rigidez! global! de! la! celosía,!
mayores!serán!los!momentos!desarrollados!en!los!cordones.!!
!  Otra!manera!de!despreciar!los!efectos!secundarios!es!recalcular!con!
todas! las! uniones! internas! rígidas,! y! ver! que! los! momentos! en! los!
extremos! son! del! orden! de! los! momentos! resultantes! del! propio!
35"
peso!de!las!diagonales.!
!
CÁLCULO%–%ANÁLISIS%GLOBAL%
Efecto%de%la%holgura%en%la%flecha%
!  Cuando! las! uniones! entre! los! elementos! que! componen! una!
celosía! son! uniones! atornilladas,! con! tornillos! trabajando! a!
cortante!(categoría!A!en!la!norma!EN!1993L1L8[2]),!la!tolerancia!
de! dichas! uniones! puede! tener! un! efecto! significa7vo! en! el!
desplazamiento!de!los!nudos.!
El!efecto!de!holgura!bajo!carga!
36"
CÁLCULO%–%ANÁLISIS%GLOBAL%
Efecto%de%la%holgura%en%la%flecha%
!  U7lizando! la! ecuación! de! Bertrand! Fontviolant! se! puede! evaluar! la!
flecha! de! una! celosía! debido! a! la! holgura,! considerando! una! carga!
unitaria!aplicada!en!el!punto!medio!de!la!luz:!
i=b
Fili
ν = ∑ N1,i
donde:!
ES i
i=1
N1,i!–!es!el!esfuerzo!axil!producido!en!un!elemento!(i)!por!una!fuerza!
unitaria!aplicada!en!el!punto!donde!la!flecha!es!requerida!
li!–!es!la!longitud!del!elemento!i!
Si!–!es!el!área!de!la!sección!del!elemento!i!
b!–!es!el!número!de!elementos!con!uniones!atornillada!
Fi li
!–!es!la!variación!en!longitud!del!elemento!i!derivada!de!la!holgura!
ES i
Igual" a" ±4" mm" dependiendo" si" el" cordón" está" comprimido" o"
traccionado"
37"
"
!
CÁLCULO%–%ANÁLISIS%GLOBAL%
Efecto%de%la%holgura%en%la%flecha%
!  La!holgura!total!en!todas!las!uniones!de!una!celosía!puede!llevar!a!
un! incremento! significa7vo! de! los! desplazamientos,! así! pues,! es!
vital!controlar!el!efecto!de!la!holgura.!
!  Para!hacerlo,!a!menudo!es!necesario:!
" 
bien! limitar! la! holgura! de! las! uniones! de! categoría! A:! u7lizar!
orificios! de! +1! mm,! incluso! +0,5! mm! y! u7lizar! tornillos! con!
vástago!sin!roscar!(para!limitar!el!incremento!de!la!holgura!por!
deformación);!o!bien!
" 
u7lizar!tornillos;!o!bien!
" 
u7lizar!tornillos!pretensados!(uniones!de!categoría!C);!o!bien!
" 
u7lizar!uniones!soldadas!en!lugar!de!uniones!atornilladas.!
38"
CÁLCULO%–%ANÁLISIS%GLOBAL%
Modificación%de%una%celosía%para%el%paso%de%equipos%
!  Ocurre! con! frecuencia! que! para! permi7r! el! paso! de! equipos! (por!
ejemplo,! un! conducto! de! gran! sección)! la! forma! de! una! celosía!
7ene!que!ser!modificada.!
!  Son!varias!las!soluciones!que!se!presentan:!
"  Se! puede! aumentar! el! área! de! paso! disponible! mediante! una!
excentricidad!en!la!unión!de!uno!de!los!cordones!(caso!1);!o!
"  "quebrando”!una!diagonal!mediante!triangulación!(caso!2).!
caso!1!
caso!2!
Local!modifica7on!of!the!truss!due!to!the!passage!of!duct!
39"
COMPROBACIÓN%DE%LOS%ELEMENTOS%
COMPROBACIÓN%DE%LOS%ELEMENTOS%A%COMPRESIÓN%
!  La%resistencia%de%un%elemento%a%compresión%se!calcula!teniendo!en!
cuenta!los!diferentes!modos!de!inestabilidad:!
" 
La!abolladura!de!la!sección!se!controla!mediante!la!clasificación!
de!las!secciones!y,!si!procede,!sus!propiedades!efec7vas!(clase!4);!
" 
Para!controlar!el!pandeo!del!elemento!se!aplica!un!coeficiente!de!
reducción! (χ)! en! el! cálculo! de! la! resistencia! de! la! sección.! Este!
factor! de! reducción! se! ob7ene! a! par7r! de! la! esbeltez! del!
elemento,!que!depende!del!esfuerzo!axil!crí7co!elás7co!(carga!de!
Euler);!
" 
En!la!mayoría!de!los!elementos!de!una!celosía!sólo!es!necesario!
evaluar!el!pandeo!por!flexión!de!los!elementos!comprimidos!en!
el!plano!de!la!celosía!y!fuera!del!plano!de!la!celosía.!
41"
COMPROBACIÓN%DE%LOS%ELEMENTOS%A%COMPRESIÓN%
Comprobación% de% la% resistencia% de% la% sección% someRda% a% compresión%
uniforme:%
NEd
!
EN!1993L1L1!§!6.2.4(1)!
≤1
donde:!
Nc,Rd
!!
!
!
!!
! ! N =! Afy
!para!secciones!de!clase!1,!2,!3!!
c,Rd
!
γ M0
!!
!
!para!secciones!de!clase!4!
EN!1993L1L1!§!6.2.4(2)!
Aeff fy
!
Nc,Rd =
γ M0
!
!NEd!es!el!valor!de!cálculo!del!esfuerzo!axil!a!compresión!
!A!es!el!área!de!la!sección!
!Aeff!es!el!área!efec7va!de!la!sección!según!EN!1993L1L5!!
!fy!–!límite!elás7co!
! γM0! –! coeficiente! parcial! para! la! resistencia! de! las! secciones!
transversales,!independientemente!de!la!clase.!
!γM0!=!1,00!
42"
COMPROBACIÓN%DE%LOS%ELEMENTOS%A%COMPRESIÓN%
EN!1993L1L1!§!6.3.1.1!
Comprobación%de%la%resistencia%a%pandeo%del%
%elemento%someRdo%a%compresión:%
NEd
!
≤1
Nb,Rd
!
donde:!
!!
!χAfy !
!!
Nb,Rd =
!!
! γ M1 !!para!secciones!de!clase!1,!2,!3!
!
χAeff fy
! ! Nb,Rd = !
!para!secciones!de!clase!4!
γ M1
!
Nb,Rd!!La!resistencia!de!cálculo!al!pandeo!del!elemento!comprimido!
χ!–!coeficiente!de!reducción!para!el!modo!de!pandeo!considerado!
γM1! –! coeficiente! parcial! para! la! resistencia! de! los! elementos! a!
inestabilidad!
γM1!=!1,00!
43"
!
COMPROBACIÓN%DE%LOS%ELEMENTOS%A%COMPRESIÓN%
Cálculo%del%coeficiente%reductor:%
%%
1
χ
=
≤1
!
2
2
φ
+
φ
−λ
donde:!
EN!1993L1L1!§!6.3.1.2!
2
φ = 0,5[1 + α (λ − 0,2) + λ ]
!
!
λ! ! ! ! ! es! la! esbeltez! adimensional! debería! determinarse! a! par7r! de! la!
curva!de!pandeo!apropiada!
! α! es! un! coeficiente! de! imperfección! que! también! debería!
determinarse!a!par7r!de!la!curva!de!pandeo!apropiada!
!
! Curva%de%pandeo%
Coef.!de!imperfección!α!
a0%
a%
b%
c%
d%
0,13!
0,21!
0,34!
0,49!
0,76!
44"
EN!1993L1L1!§!6.3.1.2!
Tabla!6.1!
COMPROBACIÓN%DE%LOS%ELEMENTOS%A%COMPRESIÓN%
Elección!de!la!curva!de!pandeo!
para!cada!sección!transversal!
EN!1993L1L1!§!6.3.1.2!Tabla!6.2!
45"
COMPROBACIÓN%DE%LOS%ELEMENTOS%A%COMPRESIÓN%
Cálculo!de!la!esbeltez!adimensional!correspondiente:! λ
!
EN!1993L1L1!§!6.3.1.2!
!
Afy Lcr 1
λ=!
=!
!!!!!!!!!!!para!secciones!de!clase!1,!2,!3!
Ncr
i λ1
!
!
!
!!
Aeff
!A f !
!!!!!!!!!!!para!secciones!de!clase!4!
L
eff y
A
cr
λ
=
=
!
Ncr
i λ1
donde:!
Lcr!!!es!la!longitud!de!pandeo!en!el!plano!de!pandeo!considerado;!!
i! !!es!el!radio!de!giro!alrededor!del!eje!considerado,!determinado!éste!
a!par7r!de!las!caracterís7cas!de!la!sección!transversal!bruta!
E
λ1 = π
= 93,9ε
fy
ε=
46"
235
fy
COMPROBACIÓN%DE%LOS%ELEMENTOS%A%COMPRESIÓN%
Cálculo%de%la%longitud%de%pandeo%
!
EN!1993L1L1!Anexo!BB!§!BB.1!
!
!
!
!!
CORDONES%
En!el!plano!
Fuera!del!plano!
!
secciones!
otras!
secciones!en! secciones!
otras!
secciones!en!
!
I!o!H!
secciones!
cajón!
I!o!H!
secciones!
cajón!
abiertas!
abiertas!
!
0,9L"
1,0L"
0,9L"
1,0Ls!
1,0Ls!
0,9Ls!
!
donde:!
L! !es!la!longitud!del!sistema!en!el!plano!(distancia!entre!nudos)!!
Ls !es!la!longitud!del!sistema!fuera!del!plano!(puntos!de!soporte!lateral)!
47"
COMPROBACIÓN%DE%LOS%ELEMENTOS%A%COMPRESIÓN%
Cálculo%de%la%longitud%de%pandeo%
!
!
!
!
!
!
!
EN!1993L1L1!Anexo!BB!§!BB.1!
DIAGONALES%Y%MONTANTES%
!!
en!el!plano!(excepto!para!angulares)!
elemento!conectado!
!en!sus!extremos!mediante!
(mínimo!2!tornillos!o!soldadura)!!
Elemento!no!
suficientamente!
conectado!
(con!1!tornillo)!!
fuera!del!plano!
para!todos!los!casos!
!
0,9L"
1,0L"
1,0L"
!
L!!es!la!longitud!del!sistema!en!el!plano!(distancia!entre!nudos)!!
!
!
48"
COMPROBACIÓN%DE%LOS%ELEMENTOS%A%COMPRESIÓN%
Montantes%y%diagonales%formados%por%angulares%EN!1993L1L1!Anexo!BB!§!BB.1.2!
!  Siempre!que!los!cordones!supongan!una!cierta!coacción!a!los!extremos!
de!los!montantes!y!diagonales!formados!por!angulares!y!que!las!uniones!
extremas! aporten! una! cierta! fijación! (al! menos! dos! tornillos! en! el! caso!
de! uniones! atornilladas)! se! podrán! despreciar! las! excentricidades! y! se!
podrá! considerar! en! el! cálculo! a! compresión! de! los! montantes! y!
diagonales!que!los!extremos!son!fijos.!!
!  La!esbeltez!efec7va!se!puede!calcular!como!sigue!:!
λ eff,v =! 0,35 +! 0,7λ v !para!pandeo!sobre!el!eje!vLv!!
λ eff,y =! 0,50 +! 0,7λ y !!para!pandeo!sobre!el!eje!yLy!
λ eff,z != 0,50 +! 0,7λ z !!para!pandeo!sobre!el!eje!zLz!
donde! !!!!!se!define!en!
EN!1993L1L1!§!6.3.1.2!
λ
!  Si! se! u7liza! un! solo! tornillo! en! las! uniones! extremas! de! montantes! o!
diagonales! cons7tuidas! por! angulares,! entonces! se! debería! considerar! la!
excentricidad!y!se!debería!tomar!como!longitud!de!pandeo!Lcr!la!longitud!
del!elemento!L.!
49"
COMPROBACIÓN%DE%LOS%ELEMENTOS%A%COMPRESIÓN%
cálculo%de%la%resistencia%a%compresión%de%elementos%%
!  es! prác7ca! habitual! fabricar! los! elementos! de! la! celosía! con! dos!
angulares!o!dos!perfiles!tubulares!(UPE);!!
!  EN! 1993L1L1! Anexo! BB! no! se! especifica! si! esta! regla! es! igualmente!
aplicable!a!elementos!compuestos!por!dos!pares!de!angulares:!como!
simplificación,! se! recomienda! usar! una! longitud! de! pandeo! de! 0,9!
veces!la!longitud!del!sistema)!;!
!  Para!asegurar!que!los!elementos!mixtos!se!comportan!como!un!único!
elemento! en! modo! de! pandeo! por! flexión,! los! 2! elementos! se! unen!
mediante!2!presillas.!
1!L!presilla!
2!L!cartela!
Elementos!compuestos!
por!2!angulares!
50"
COMPROBACIÓN%DE%LOS%ELEMENTOS%A%COMPRESIÓN%
!  Los!elementos!compuestos!deben!unirse!sin!holgura;!
!  El! hueco! entre! los! angulares,! y! el! espesor! de! las! presillas,! debe! ser!
igual! al! espesor! de! la! cartela! a! la! que! el! elemento! armado! está!
conectado;!
!  Según!
la! norma! EN! 1993L1L1,! el! espaciamiento! máximo! entre! las!
uniones! de! elementos! está! limitado! a! 15! veces! el! radio! de! giro!
mínimo! de! los! dos! elementos! aislados.! Si! no,! deben! llevarse! a! cabo!
comprobaciones! más! complejas,! en! las! que! se! debe! considerar! la!
rigidez!a!cortante!del!elemento!armado.!
51"
COMPROBACIÓN%DE%LOS%ELEMENTOS%A%COMPRESIÓN%Y%FLEXIÓN%
Comprobación%de%la%resistencia%de%la%sección%someRda%a%momento%
!
MEd
≤1
EN!1993L1L1!§!6.2.5!
donde:!
Mc,Rd
!
Wpl fy
Mc,Rd =! !Mpl,Rd =!
!!!!!para!secciones!de!clase!1!o!2!
γ M0
!
Wel,min fy
Mc,Rd =! M
! el,Rd = !
!!!!!para!secciones!de!clase!3!
γ M0
! Weff,min fy
Mc,Rd =! !
!
!!!!!para!secciones!de!clase!4!
γ
!
M0
MEd!!es!el!valor!de!cálculo!del!momento!flector!!
Wpl!–!módulo!resistente!plás7co!
correspondientes!a!
Wel,min!–!módulo!resistente!mínimo!
la!fibra!con!máxima!
Weff,min!–!módulo!resistente!máximo!
tensión!elás7ca!
!
52"
COMPROBACIÓN%DE%LOS%ELEMENTOS%A%COMPRESIÓN%Y%FLEXIÓN%
EN!1993L1L1!§!6.2.9!
Esfuerzo%axil%y%flexión%
!  Para!secciones!de!clase!1!o!2:! M ≤ M
Ed
N,Rd
MN,Rd!es!la!resistencia!plás7ca!de!cálculo!a!flexión!reducida,!debido!a!la!
existencia!del!esfuerzo!axil!NEd,!!
Para! secciones! transversales! en! las! cuales! los! agujeros! para! los!
elementos! de! unión! no! sean! considerados,! pueden! aplicarse! las!
siguientes!expresiones!aproximadas!para!perfiles!laminados!estándares!
en!I!o!en!H!y!para!secciones!soldadas!en!I!o!H!con!alas!iguales.!
MN,y,Rd = Mpl, y,Rd (1 − n) /(1 − 0,5a) MN,y,Rd ≤ Mpl, y,Rd
!
MN,z,Rd = Mpl,z,Rd
!
& , n − a )2 #
para!n!≤!a:!!M
' !
N,z,Rd = Mpl,z,Rd $1 − *
$% + 1 − a ( !"
para!n!>!a:!!
donde:!n!=!NEd/Npl,Rd!
!a!=!(AL2btf)/A!!!pero!a!≤!0,5!
Para!otras!secciones!ver!EN!1993L1L1!§!6.2.9(5)!
53"
!
COMPROBACIÓN%DE%LOS%ELEMENTOS%A%COMPRESIÓN%Y%FLEXIÓN%
EN!1993L1L1!§!6.2.9!
fy
Esfuerzo%axil%y%flexión%
σ x,Ed ≤
!  Para!secciones!de!clase!3:!
γ M0
σx,Ed! ! es! el! valor! de! cálculo! de! la! tensión! longitudinal! debida! al!
momento!y!al!esfuerzo!axil,!teniendo!en!cuenta!los!agujeros!para!
los! elementos! de! unión! cuando! éstos! sean! relevantes! (ver! EN!
1993L1L1!§!6.2.4!y!§!6.2.5);!!
!  Para! secciones! de! clase! 4! la! tensión! σx,Ed! se! calcula! con! los! valores!
efec7vos!y!deberá!cumplir!el!siguiente!criterio:!
!
My,Ed + NEdeNy
Mz,Ed + NEdeNz
NEd
+
+
≤1
!
Aeff fy / γ M0 Weff,y,min fy / γ M0 Weff,z,min fy / γ M0
donde:!
eN! es! el! desplazamiento! del! centro! de! gravedad! cuando! la!
sección!transversal!se!ve!some7da!solamente!a!compresión!
uniforme!
54"
COMPROBACIÓN%DE%LOS%ELEMENTOS%A%COMPRESIÓN%Y%FLEXIÓN%
Comprobación%de%la%resistencia%de%la%sección%a%cortante%
!
EN!1993L1L1!§!6.2.6!
VEd
"  En!ausencia!de!torsión,!la!resistencia!plás7ca:!
≤1
Vc,Rd
Av ( fy / 3)
Vc,Rd = Vpl,Rd =
!
γ M0
τ Ed
≤ 1,0
Para!la!comprobación!de!la!resistencia!elás7ca:!
fy /( 3γ M0 )
V
! V S
!
!
!
!!
Ed
τ Ed =! Ed !para!secciones!IL!H:!!! !!! τ Ed = !!!!!!!!!!!!!!!!!!!!!!!si!!A /A ≥0,6!
Aw
f w
I ×t
donde:!VEd!es!el!valor!del!cálculo!del!esfuerzo!cortante!
"Av!es!el!área!a!cortante!según! EN!1993L1L1!§!6.2.6(3)!
"S!es!el!momento!está7co!de!la!sección!
"I!es!el!momento!de!inercia!de!la!sección!transversal!
"t!es!el!espesor!del!punto!considerado!
"Af!es!el!área!de!un!ala!
"Aw!es!el!área!del!alma:!Aw!=!hwtw!
"hw,!tw!es!la!altura!y!espesor!del!alma!respec7vamente,!
55"
" 
COMPROBACIÓN%DE%LOS%ELEMENTOS%A%COMPRESIÓN%Y%FLEXIÓN%
Influencia% del% esfuerzo% cortante% en% la% resistencia% a% flexión% de% la%
sección%
EN!1993L1L1!§!6.2.10!
!
!  Si!VEd!≤!0,5Vpl,Rd!y!hw/tw!≤!72ε/η!(para!η!ver EN!1993L1L5!
!!!!!!!!!o!del!lado!de!
la!seguridad:!η!=!1,0),!no!es!necesario!considerar!una!reducción!de!
EN!1993L1L1!§!6.2.9!
la!resistencia!a!flexión!de!la!sección.!
!  Si!VEd!>!0,5Vpl,Rd!!la!resistencia!reducida!a!flexión!debería!obtenerse!
como! la! resistencia! de! cálculo! de! la! sección! transversal,!
determinada! u7lizando! un! límite! elás7co! reducido! (1Lρ)fy! para! el!
área!a!cortante,!donde:!
!!
!&
!! #2
2V
ρ = $$ Ed − 1 !!
% Vpl,Rd
"
56"
COMPROBACIÓN%DE%LOS%ELEMENTOS%A%COMPRESIÓN%Y%FLEXIÓN%
Comprobación% de% la% resistencia% a% pandeo% de% elementos% someRdos% a%
compresión%y%flexión%
EN!1993L1L1!§!6.3.3!
%
My,Ed + ΔMy,Ed
Mz,Ed + ΔMz,Ed
NEd
%
+ kyy
+ kyz
≤1
χ y NRk
My,Rk
Mz,Rk
%
%
%
%
%
%
%
γ M1
χLT
γ M1
γ M1
My,Ed + ΔMy,Ed
Mz,Ed + ΔMz,Ed
NEd
+ kzy
+ kzz
≤1
χ zNRk
My,Rk
Mz,Rk
χLT
γ M1
γ M1
γ M1
donde:!!
NEd,!My,Ed!and!Mz,Ed!son!los!valores!de!cálculo!del!esfuerzo!axil!de!compresión!y!
de! los! momentos! flectores! máximos! a! lo! largo! del! elemento,!
alrededor!de!los!ejes!yLy!y!zLz!respec7vamente;!
ΔMy,Ed,!ΔMz,Ed!son!los!momentos!debidos!al!desplazamiento!del!eje!del!centro!
de!la!gravedad,!según!6.2.9.3,!en!las!secciones!de!Clase!4;!
!Χy!y!Χz!son!los!coeficientes!de!reducción!para!pandeo!por!flexión!según!§!6.3.1!
ΧLT!es!el!coeficiente!de!reducción!para!pandeo!lateral,!según!§!6.3.2!
kyy,!kyz,!kzy,!kzz!son!los!coeficientes!de!interacción.!
57"
COMPROBACIÓN%DE%LOS%ELEMENTOS%A%COMPRESIÓN%Y%FLEXIÓN%
! 
%
%
%
%
%
!
Valores!para!NRk!=!fyAi,!Mi,Rk!=!fyWi!y!ΔMi,Ed!
EN!1993L1L1!§!6.3.3!
Class%
1%
2%
3%
4%
Ai!
A"
A"
A"
Aeff!
Wy!
Wpl,y!
Wpl,y!
Wel,y!
Weff,y!
Wz!
Wpl,z!
Wpl,z!
Wel,z!
Weff,z!
ΔMy,Ed!
0!
0!
0!
eN,yNEd!
ΔMz,Ed!
0!
0!
0!
eN,zNEd!
!  Los!coeficientes!de!interacción!kyy,!kyz,!kzy,!kzz!se!han!obtenido!a!par7r!
de!dos!aproximaciones!alterna7vas!al!problema.!Los!valores!de!estos!
coeficientes!pueden!obtenerse!del!anexo!A!(método!alterna7vo!1)!o!
del! anexo! B! (método! alterna7vo! 2).! El! anexo! nacional! puede! elegir!
entre! ambos! métodos! alterna7vos.! En! aras! de! conseguir! una! mayor!
simplicidad,! las! comprobaciones! pueden! efectuarse! en! el! rango!
elás7co!únicamente.!
58"
COMPROBACIÓN%DE%LOS%ELEMENTOS%A%TRACCIÓN%
Comprobación%de%elementos%a%tracción%
NEd
≤1
N t,Rd
EN!1993L1L1!§!6.2.3!
!!
donde:!
Nt,Rd!L!la!resistencia!de!cálculo!a!tracción!
!
Af y
!  Para!uniones!soldadas:! N
!
!!
t,Rd = Npl,Rd =
γ M0
EN!1993L1L8!§!3.1.1(4)!
!!
!  Para!uniones!atornilladas,!según!el!7po!de!unión:!
!Categoría%A!:!Resistentes!al!aplastamiento!
! !Categoría%B!:!Resistentes!al!deslizamiento!en!el!E.L.S.!
%%%%%Categoría%C!:!Resistentes!al!deslizamiento!en!el!E.L.U.!
!
59"
COMPROBACIÓN%DE%LOS%ELEMENTOS%A%TRACCIÓN%
Resistencia%de%elementos%a%tracción%atornillados%
!  Es!necesario!introducir!el!concepto!de!área!neta!
EN!1993L1L1!§!6.2.3!
!  Para! secciones! con! agujeros,! y! para! las! categorías! A! y! B,! el! valor! de!
cálculo!del!esfuerzo!axil!de!tracción!!Nt,Rd:!
!
Afy
$
la!resistencia!plás7ca!de!cálculo!de!la!sección!transversal!
!! Npl,Rd = γ
bruta!
M0
Nt,Rd = min#
0,9 Anet fu la!resistencia!úl7ma!de!cálculo!de!la!sección!transversal!
!Nu,Rd =
neta,! considerando! los! agujeros! para! los! elementos! de!
!
!"
γ M2 unión!
!  Para! la! categoría! C! el!! valor! de! cálculo! del! esfuerzo! axil! de!
tracciónNt,Rd:!
Anet! fy
Anet = A − tnd0
N
=
N
=
t,Rd
net,Rd
!
donde:!
γ M0
t!espesor!del!elemento!
n!núm.!de!agujeros!alineados!ver7calmente!
d0!diámetro!del!agujero!
A!–!área!bruta!de!la!sección!
Anet!–!área!neta!de!la!sección!
γM2!=1,25!–!coeficiente!parcial!de!resistencia!!de!la!sección!neta!
60"
!
COMPROBACIÓN%DE%LOS%ELEMENTOS%A%TRACCIÓN%
Resistencia%de%elementos%a%tracción%atornillados%
Angulares%unidos%por%un%lado%
EN!1993L1L8!§!3.10.3!
!  Un! angular! único! a! tracción! unido! por! una! única! fila! de! tornillos!
en! un! lado,! puede! tratarse! como! cargado! concéntricamente! en!
una! !sección!neta!eficaz!para!la!cual!el!valor!de!cálculo!úl7mo!de!
la!resistencia!debería!determinarse!de!la!siguiente!manera:!
!
con%1%tornillo%
con%2%tornillos%
con%3%tornillos%
!
Nu,Rd =
2,0(e2 − 0,5d0 )t × fu
γ M2
β2 Anet × fu
Nu,Rd =
γ M2
β 3 Anet × fu
Nu,Rd =
γ M2
donde:!
β2!y!β3!son!coef.!de!reducción!que!dependen!de!la!separación!p1!
Anet!es!el!área!neta!del!angular.!Para!un!angular!de!lados!desiguales!
unidos!por!su!lado!menor,!Anet!debería!tomarse!igual!al!área!neta!de!
la!sección!de!un!angular!de!lados!iguales!equivalente!con!los!lados!
del!mismo!tamaño!que!el!lado!menor.!
61"
COMPROBACIÓN%DE%LOS%ELEMENTOS%A%TRACCIÓN%
Resistencia%de%elementos%a%tracción%atornillados%
Angulares%unidos%por%un%lado%
!
!
EN!1993L1L8!§!3.10.3!
(a)!1!tornillo!
(b)!2!tornillos!
(c)!3!tornillos!
separación%%%%%p1%
≤%2,5d0%
≥%5,0d0%
EN!1993L1L8!§!3.10.3!Tabla!3.8!
!
!
! !
2!tornillos!!!!!β
0,4!
0,7! ! Para! valores! intermedios! de! p1! el! valor! de ! ! !
2!
!
!puede!interpolarse!linealmente!
3!tornillos!o!más!!!β3! 0,5!
0,7!
!  Una! consideración! similar! debería! darse! también! para! otro! 7po! de!
secciones!unidas!a!través!de!las!alas!voladas!
62"
COMPROBACIÓN%DE%LOS%ELEMENTOS%A%TRACCIÓN%Y%FLEXIÓN%
Comprobación%de%elementos%a%tracción%y%flexión%
EN!1993L1L1!§!6.2.1(7)!
NEd
MEd
+
≤1
EN!1993L1L1!§!6.2.3!
donde:!
Nt,Rd Mc ,Rd
EN!1993L1L1!§!6.2.5!
Nt,Rd!L!!resistencia!de!cálculo!a!tracción!!
Mc,Rd!L!resistencia!de!cálculo!a!flexión!considerando!agujeros!
Considerción%de%los%agujeros%en%la%resistencia%a%flexión%
!  Los! agujeros! para! los! elementos! de! unión! en! el! ala! traccionada!
pueden!ignorarse!siempre!que!para!dicha!ala!se!cumpla!que:! !!
Af,net × 0,9 fu Af fy
!
≥
γ M2
γ M0
donde:!
Af!–!área!del!ala!tracccionada!
!  Los!agujeros!para!los!elementos!de!unión!en!la!zona!comprimida!de!la!
sección!transversal,!excepto!los!sobredimensionados!o!alargados,!no!
necesitan!ser!considerados,!siempre!que!los!agujeros!estén!ocupados!
por!los!elementos!de!unión.!
!!
63"
COMPROBACIÓN%DE%UNIONES%
COMPROBACIÓN%DE%UNIONESd%%UNIONES%ATORNILLADAS%
!  Categorías!de!uniones!atornilladas!
Categoría%
Criterio%
EN!1993L1L8!!Tabla!3.2!
Comentarios%
Uniones!a!cortante!
A!–!Resistentes!al!
aplastamiento!!
B!–!resistentes!al!
deslizamiento!!
!en!el!ELS!
C!–!resistentes!al!
deslizamiento!!
En!ELU!
Fv,Ed!≤!Fv,Rd!
Fv,Ed!≤!Fb,Rd!
No!se!requiere!pretensado.!
Pueden!u7lizarse!tornillos!de!clases!4.6!a!10.9.!
Fv,Ed,ser!≤!Fs,Rd,ser! Deberían!u7lizarse!tornillos!pretensados!de!
clases!8.8!o!10.9.!Para!la!resistencia!al!
Fv,Ed!≤!Fv,Rd!
deslizamiento!en!ELS,!véase!el!apartado!3.9.!
Fv,Ed!≤!Fb,Rd!
Fv,Ed!≤!Fs,Rd!
Fv,Ed!≤!Fb,Rd!
Fv,Ed!≤!Nnet,Rd!
Deberían!u7lizarse!tornillos!pretensados!de!
clases!8.8!o!10.9.!Para!la!resistencia!al!
deslizamiento!en!ELU,!véase!el!apartado!3.9.!
Nnet,Rd!véase!el!punto!c)!del!apartado!(1)!
Uniones!a!tracción!
D!–!sin!prestensar!
Ft,Ed!≤!Ft,Rd!
Ft,Ed!≤!Bp,Rd!
No!se!requiere!pretensado.!Pueden!u7lizarse!
tornillos!de!clases!4.6!hasta!10.9.!Bp,Rd!véase!la!
tabla!3.4.!
E!–!pretensadas!
Ft,Ed!≤!Ft,Rd!
Ft,Ed!≤!Bp,Rd!
Deberían!u7lizarse!tornillos!pretensados!de!
clases!8.8!o!10.9.!.!Bp,Rd!!véase!la!tabla!3.4.!
65"
COMPROBACIÓN%DE%UNIONESd%%UNIONES%ATORNILLADAS%
!  Resistencia%de%cálculo%de%elementos%individuales%a%cortante%
"  Fv,Rd%d%Resistencia%a%cortante%por%el%plano%de%cortante%
!
Fv,Rd =
α v fub A
γ M2
cuando!el!plano!de!cortante!pasa!por!la!parte!roscada!del!tornillo!(A!es!
el!área!traccionada!del!tornillo!As):!
L!!!αv!=!0,6!para!clases!4.6,!5.6.!8.8!
L  αv!=!0,5!para!clases!4.8,!5.8.!10.9!
cuando!el!plano!de!cortante!pasa!por!la!parte!roscada!del!tornillo!(A!es!
el!área!traccionada!del!tornillo!As):αv!=!0,6!!
k1α b fudt
"  !Fb,Rd%–%Resistencia%a%aplastamiento%
Fb,Rd =
γ M2
!
& p2
#
& e1 fub
#
e2
$
$
!
k1 = min$ 1,4 − 1,7; 2,8 − 1,7; 2,5 !!
αb = min$
; ;1,0 !
d0
"
% 3d0 fu
"←!tornillos!extremos→! % d0
& p1 1 fub
#
& p2
#
$
!
$
αb = min$
− ; ;1,0 !
k1 = min$ 1,4 − 1,7; 2,5 !!
66"
% 3d0 4 fu
" tornillos!interiores→!
% d0
"
COMPROBACIÓN%DE%UNIONESd%%UNIONES%ATORNILLADAS%
!  Símbolos%para%distancias%a%los%bordes%y%separación%entre%elementos%
de%fijación%
* e1 ' # 4t + 40mm Para!estructuras!de!acero!de!acuerdo!con!EN!10025!
excepto!para!aceros!de!acuerdo!con!EN!10025L5!
1,2d0 ≤ (( %% ≤ "
) e2 & !8t%or%125mm Para!estructuras!de!acero!de!acuerdo!con!EN!10025L5!
Separación!al!tresbolilloL!compresión!
1!–!fila!exterior,!2!–!fila!interior!
Separación!al!tresbolilloL!tracción!
2,2d0 ≤ p1 ≤ min(14t ,200mm)
28t
# 14t
#
2,4d0 ≤ p2 ≤ min(14t ,200mm) p1,0 ≤ min"
p1,i ≤ min"
!200mm
!400mm
67"
COMPROBACIÓN%DE%UNIONESd%%UNIONES%ATORNILLADAS%
!  Arrancamiento%de%bloque%(desgarro)%
El! desgarro! consiste! en! el! fallo! a! cortante! en! la! fila! de! tornillos! situada! a! lo!
largo! del! plano! que! delimita! el! esfuerzo! a! cortan! del! grupo! de! agujeros!
acompañado! por! la! rotura! a! tracción! de! la! fila! de! agujeros! situada! a! lo! largo!
del!plano!que!delimita!el!esfuerzo!a!tracción!del!grupo!de!tornillos.!
!
1!–!fuerza!de!tracción!pequeña!
2!–!fuerza!cortante!grande!
3!–!fuerza!cortante!pequeña!
4!–!fuerza!de!tracción!grande!
!
Ant!área!neta!some7da!a!tracción!
Anv!área!neta!some7da!a!cortante!
%
%
%
%
%
%
"  Para! un! grupo! de! tornillos! simétrico! sujeto! a! cargas! concéntricas! Veff,1,Rd!
será:!
(
)
VEd ≤ Veff,1,Rd = fu Ant / γ M2 + 1 / 3 fy Anv / γ M0
(
)
"  Para!un!grupo!de!tornillos!sujeto!a!cargas!excéntricas,!V
VEd ≤ Veff,2,Rd = 0,5 fu Ant / γ M2 + 1 / 3 fy Anveff,2,Rd
/ γ M0!será:!
68"
COMPROBACIÓN%DE%UNIONESd%%UNIONES%ATORNILLADAS%
!  Resistencia%de%cálculo%de%elementos%individuales%a%tracción%
"  Bp,Rd%–%resistencia%al%punzonamiento%
Bp,Rd = 0,6πdmtp fu / γ M2
donde:! dm! es! la! media! de! las! distancias! entre! los! vér7ces! y! entre! las!
caras! planas! de! la! cabeza! del! tornillo! o! de! la! tuerca,! la! que!
sea!menor;!
tp!es!el!espesor!de!la!chapa!bajo!el!tornillo!o!la!tuerca;!
"  Ft,Rd%–%resistencia%a%tracción
Ft,Rd
=!!
k2 fub As
γ M2
!donde:!k2!=!0,63!para!tornillos!de!cabeza!avellanada!k2!=!0,9.!
!  Cortante%y%tracción%combinadas%
Fv,Ed
Ft,Ed
+
≤ 1,0
Fv,Rd 1,4Ft,Rd
69"
COMPROBACIÓN%DE%UNIONESd%%UNIONES%ATORNILLADAS%
!  Resistencia%al%cálculo%al%deslizamiento%
EN!1993L1L1!§!3.9.1!
k nµ
Clase%de%la%superf.%
donde:!!
Fs,Rd = s Fp,C
de%rozamiento%%
γ M3
(ver%EN%1090)%
n!!!nº!de!planos!de!rozamiento!
A!
Fp,C!!!!fuerza!de!pretensado! Fp,C = 0,7 fub As
B!
μ!!coef.!de!rozamiento!EN!1993L1L8!Table!3.7!
C!
ks!!!es!el!valor!de!!EN!1993L1L8!Table!3.6!
D!
γM3!=1,25!–!coef.!parcial!de!resistencia!al!deslizamiento!
Coef.%
Rozamid
ento%μ%
Descripción%
0,5!
0,4!
0,3!
0,2!
ks%
Tornillos!en!agujeros!normalizados!!
1,0!
Tornillos!en!agujeros!con!holguras!o!agujeros!alargados!cortos!con!el!eje!del!alargamiento!en!
dirección!perpendicular!a!la!de!transferencia!de!la!carga!!
0,85!
Tornillos!en!agujeros!alargados!largos!con!el!eje!del!alargamiento!en!dirección!perpendicular!
a!la!!de!transferencia!de!la!carga!!
0,7!
Tornillos!en!agujeros!alargados!cortos!con!el!eje!del!alargamiento!en!dirección!paralela!a!la!de! 0,76!
transmisión!de!la!carga!!
Tornillos!en!agujeros!alargados!largos!con!el!eje!del!alargamiento!en!dirección!paralela!a!la!de! 0,63!
70"
transmisión!de!la!carga!!
COMPROBACIÓN%DE%UNIONESd%%UNIONES%SOLDADAS%
!  Resistencia%de%cálculo%de%las%soldaduras%en%ángulo
!
EN!1993L1L8!!
!!
!§!4.5.3.2(6)!
"  Se! asume! una! distribución! uniforme! de! tensión! en! la! sección! de! la!
garganta! de! la! soldadura! resultando! en! las! tensiones! normales! y!
tensiones!tangenciales!
σ ⊥ !es!la!tensión!normal!perpendicular!a!la!garganta!de!la!soldadura;!
τ ⊥ !es!la!tensión!tangencial!perpendicular!al!eje!de!la!soldadura;!
τ ΙΙ !es!la!tensión!tangencial!paralela!al!eje!de!la!soldadura.!
σ ΙΙ
La!tensión!normal!!!!!!paralela!al!eje!no!se!considera!cuando!se!verifica!el
!
valor!de!cálculo!de!la!resistencia!de!la!soldadura.!
"  El!valor!de!cálculo!de!la!resistencia!de!la!soldadura!será!suficiente!si!
se!cumplen!las!siguientes!condiciones:!
! = σ! 2 + 3 τ!2 + τ 2 ≤! f /(β ! γ ) !y!
σ
w
⊥
(
⊥
II
)
u
w M2
σ ⊥ ≤ 0,9 fu / γ M2
donde:!βw!es!el!coef.!de!correlación!correspondiente!tomado!en! Tabla!4.1!
71"
EN!1993L1L8!
!
!
COMPROBACIÓN%DE%UNIONESd%%UNIONES%SOLDADAS%
EN!1993L1L8!!Tabla!4.1!
!
Tipos!de!acero!
Factor!de!correlación!
72"
CONCLUSIÓN%
CONCLUSION%
!  El%
uso% de% celosías% permite% construir% edificios% de% todos% los%
tamaños%y%formas.%
!  En% esta% presentación% se% ofrecen% consejos% sobre% el% cálculo% de%
celosías% para% edificios% de% una% sola% planta% incluidas% las%
cuesRones%relacionadas%con%detalles%construcRvos,%el%análisis%
global,% así% como% la% verificación% de% los% elementos% (cordones,%
montantes% y% diagonales)% y% uniones% (empalmes,% uniones% de%
diagonales%y%montantes%con%los%cordones)%.%
%
!
74"
REFERENCIAS%
REFERENCIAS%
!  EN!1993L1L1!–!Eurocode!3!Design!of!steel!structures!Part!1L1:!
General!rules!and!rules!for!buildings!!
!  EN!1993L1L8!–!Eurocode!3!Design!of!steel!structures!–!Part!1L8:!
Design!of!joints.!!
!
!
76"
Los%módulos%pedagógicos%SKILLS%han%sido%desarrollados%por%un%consorcio%de%organismos,%cuyos%logos%figuran%al%pie%de%
esta%página.%El%material%está%publicado%bajo%una%licencia%CreaRve%Commons%
%
El%proyecto%ha%sido%parcialmente%financiado%por%la%Comisión%Europea.%%
Este%módulo%pedagógico%refleja%únicamente%la%opinión%de%sus%autores.%La%Comisión%Europea%no%asume%ninguna%
responsabilidad%de%ningún%Rpo%por%el%uso%que%se%pueda%hacer%de%la%información%contenida%en%este%módulo%pedagógico.%%%%