Diapositiva 1 - Pasión por Estudiar
Anuncio
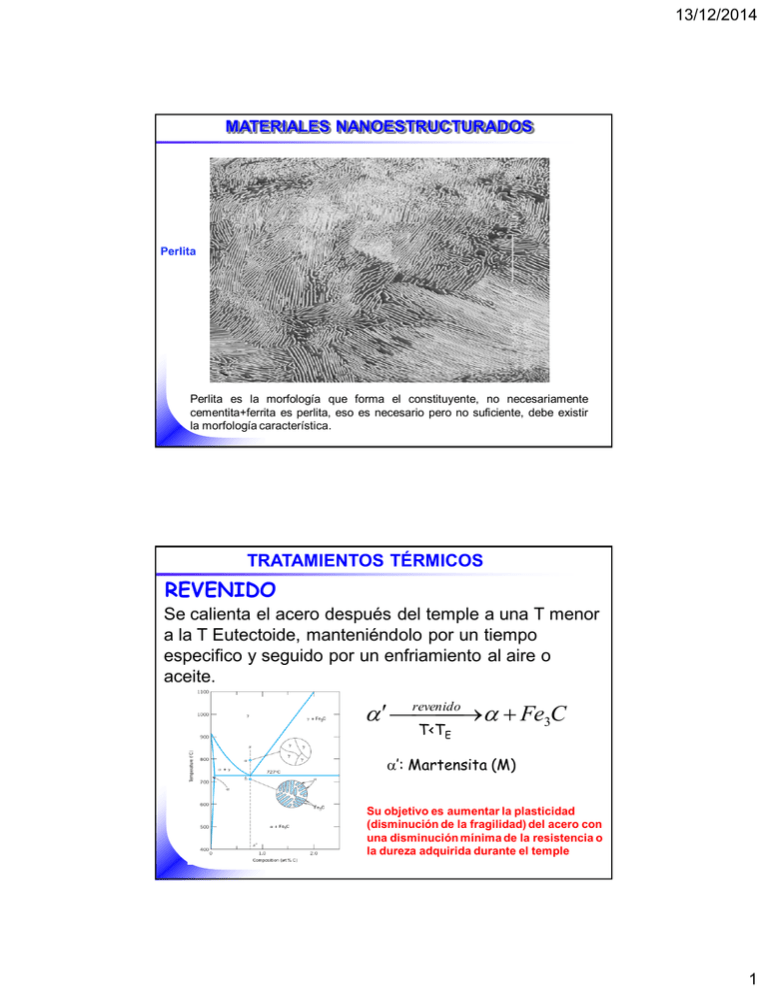
13/12/2014 MATERIALES NANOESTRUCTURADOS Perlita Perlita es la morfología que forma el constituyente, no necesariamente cementita+ferrita es perlita, eso es necesario pero no suficiente, debe existir la morfología característica. TRATAMIENTOS TÉRMICOS REVENIDO Se calienta el acero después del temple a una T menor a la T Eutectoide, manteniéndolo por un tiempo especifico y seguido por un enfriamiento al aire o aceite. revenido Fe3C T<TE ’: Martensita (M) Su objetivo es aumentar la plasticidad (disminución de la fragilidad) del acero con una disminución mínima de la resistencia o la dureza adquirida durante el temple 1 13/12/2014 TRATAMIENTOS TÉRMICOS REVENIDO + Fe3C PERLITA Distribución de partículas finas de Fe3C en una matriz conocida como MARTENSITA REVENIDA Dureza mayor que la perlita fina, Ductilidad mayor que la Martensita Dureza y Ductilidad controlada por T Revenido y tiempo. A mayor T ó t mayor ductilidad, menor resistencia TRATAMIENTOS TÉRMICOS MARTENSITA REVENIDA Fe3C Ferrita- 2 13/12/2014 Diagrama TTT para acero Eutectoide TEMPLE Austenita Estable Dureza RC 65 to ràpido enfriamien ' ’: Martensita (M) Extremadamente rápido, no toca las curvas-C Ms Austenita inestable A+M Mf M TRANSFORMACIÓN MARTENSITICA Dureza Martensita como función del contenido C Dureza, RC 60 40 20 0.2 0.4 0.6 Wt % Carbón → Dureza de la Martensita depende principalmente del contenido de C y no de otras adiciones de aleantes 3 13/12/2014 Microestructuras de la Martensita Bajo C Velocidad enfriamiento Fe-Ni Medio C Austempering Bainita Pequeñas agujas de Fe3C encajadas en placas de ferritas 4 13/12/2014 Austempering TRATAMIENTOS TÉRMICOS PROBLEMAS EN EL TEMPLADO Temple de un componente de acero 5 13/12/2014 TRATAMIENTOS TÉRMICOS PROBLEMAS EN EL TEMPLADO Agrietamiento durante el temple Altas Velocidades de enfriamiento: Superficie más fría que el interior Superficie forma Martensita antes que el interior Austenita Martensita Expansión de volumen Cuando el interior se trasforma, la capa exterior dura de martensita constriñe esta expansión ocasionando esfuerzo residuales (Supf. en tensión mientras parte central es comprimida). TRATAMIENTOS TÉRMICOS PROBLEMAS EN EL TEMPLADO Solución al agrietamiento por templado Desplazar la curva-C a la derecha (Mayores tiempos) Más tiempo antes de la Nariz Templado más lento (ej. Temple en aceite) Pero, ¿Cómo desplazar la curva-C a Mayores tiempo? 6 13/12/2014 TRATAMIENTOS TÉRMICOS PROBLEMAS EN EL TEMPLADO Solución al agrietamiento por templado Mediante Elementos Aleantes Todos los elementos aleantes en el acero (Cr, Mn, Mo, Ni, Ti, W, V), etc, desplazan las curvas-C hacia la derecha (retrasan la formación de perlita y bainita, mejorando la templabilidad del acero). Excepto: Co Temperatura (oC) Efecto de elementos aleantes en curvas TTT Tiempo (s) Los elementos aleantes retrasan la formación de Perlita y Bainita, mejorando la templabilidad del acero. 7 13/12/2014 Efecto de elementos aleantes en curvas TTT 800 2 1 3 Temperatura / C 700 4 5 6 600 500 1. Fe-0.4C 2. Fe-0.4C-2Si 3. Fe-0.4C-1Ni 4. Fe-0.4C-1Mn 5. Fe-0.4C-1Mn-1Cr 6. Fe-0.4C-2Mn 400 300 200 0 10 1 10 2 10 3 10 4 5 10 10 Tiempo / s Aceros al carbono Aceros aleados Los aleantes desplazan las curvas-C a la derecha. Separan las curvas-C para Perlita y Bainita 8 13/12/2014 PROBLEMAS EN EL TEMPLADO ¿Otra Solución al agrietamiento por templado? MARTEMPLADO Ó MARREVENIDO Homogenización Temperatura 9 13/12/2014 TEMPERATURA MARTEMPLADO Ó MARREVENIDO TIEMPO El patrón de crecimiento natural de un albor esfuerzo residuales 10 13/12/2014 TEMPLABILIDAD Habilidad ó facilidad de endurecer un acero mediante la formación de Martensita usando un temple tan lento como sea posible. Los aceros aleados tienen mayores templabilidad que los aceros al carbono comunes. Templabilidad vs Dureza ¿Sinónimo? TEMPLABILIDAD VS DUREZA Templabilidad Habilidad o facilidad de endurecer un acero Solamente se aplica a aceros Dureza Resistencia a la deformación plástica medida por indentación Aplicable a todos los materiales LAS ADICIONES DE ALEANTES INCREMENTAN LA TEMPLABILIDAD DE LOS ACEROS PERO NO LA DUREZA ¿Plasticidad vs ductilidad? 11 13/12/2014 SENSIBILIDAD AL TEMPLE - Facilidad con que el soluto escapa de la SSS durante el temple - La función del temple es retener todo el soluto sin que escape de la SSS. Energía Q Energía !Cristalografía! Q' El Q alto es el secreto para mantener estructuras metalúrgicas metaestables. A mayor templabilidad menor sensibilidad al temple. ¿Si una aleación es muy sensible al temple, hacia donde se mueve la nariz de las curvas-C? ¿Cuál de las dos energías de activación Q ò Q' es más favorable para la función del temple? ¿Quién de las dos preserva más fácilmente la estructura sobresaturada de soluto? (Termodinámicamente metaestable, pero estable cinéticamente) ESPACIOS INTERSTICIALES EN REDES ESPACIALES ¿Estructura? ¿Tipo solución? ¿Constituyente? Átomo de Carbono en una posición intersticial octaédrica 12 13/12/2014 HUECOS INTERSTICIALES EN LA ESTRUCTURA FCC SITIOS INTERSTICIALES OCTAÉDRICO SITIOS INTERSTICIALES TETRAÉDRICO Átomos Fe Intersticios octaédrico (4) Átomos Fe Intersticios tetraédrico (8) (Punto medio de cada borde y en el centro) Fracción de empaquetamiento de FCC: 0,74 (Entre una esquina y tres átomos centrados en la cara) HUECOS INTERSTICIALES EN LA ESTRUCTURA BCC SITIOS INTERSTICIALES OCTAÉDRICO (6) SITIOS INTERSTICIALES TETRAÉDRICO (12) Fracción de empaquetamiento de BCC: 0,68 (32% espacio vacío) 13 13/12/2014 ESTRUCTURA BCC Primeros vecinos (0,5 x a) Segundos vecinos Primeros vecinos (0,71 x a) 0,56 x a Hueco octaédrico irregular lleva a una distorsión tetragonal (s anisotrópico) Hueco ~2 veces más grande (Expansión isotrópica – vecinos equidistantes) HUECOS INTERSTICIALES EN LA ESTRUCTURA BCC Diferentes formas de ubicar los intersticios octaédricos en cada cara de la celda BCC 14 13/12/2014 SITIOS INTERTICIALES EN LA ESTRUCTURA BCC C ÁTOMOS DE CARBONO EN SITIOS INTERSTICIALES OCTAÉDRICOS Sitios intersticiales para el C en el Fe TAMAÑO MÁXIMO DE LA ESFERA QUE PUEDE ENTRAR EN LOS INTERSTICIOS RADIO DEL SITIO RADIO DEL SITIO PARA EL Fe (Å) Tetraédrico 0.291 r 0.37 Octaédrico 0.154 r 0.19 Tetraédrico 0.225 r 0.28 Octaédrico 0.414 r 0.52 ESTRUCTURA INTERSTICIO BCC (32% espacio vacío) FCC (26% espacio vacío) r =radio atómico del Fe- (1.28 Å). Es interesante notar que la estructura FCC aunque más compacta, tiene cavidades más grande que la bcc > solubilidad Fe-. El C ocupa los sitios octaédrico tanto en FCC y BCC, a pesar de que en BCC el espacio octaédrico es más pequeño que el tetraédrico. 15 13/12/2014 Sitio intersticial Tetraédrico para el C en el Fe NC: 4 ESTRUCTURA BCC Fe C Espacio disponible 16 13/12/2014 Sitios intersticiales para el C en el Fe NC: 6 17 13/12/2014 ¿Por qué la Martensita tiene una estructura tetragonal? En los intersticio tetraédrico (BCC), 4 átomos de Fe tienen estatus de vecinos más cerca y el desplazamiento de estos requeriría más energía de distorsión. La inserción de un átomo de C dentro de un intersticio tetraédrico causaría un desplazamiento de todos los 4 átomos que lo rodean, consecuentemente estos intersticio no son sitios preferidos por los átomos de C y N. Por otro lado, si un átomo de C es insertado dentro de un intersticio octaédrico, solamente los dos átomos de Fe localizados más cercas de él serían desplazados, causando una distorsión de la red que puede ser aliviada por una expansión de la red en la dirección de los átomos más cercanos. Esto origina una distorsión anisotrópica que puede explicar la tetragonalidad de la martensita (BCT). Si todos los átomos de C ocupan el mismo tipo de sitio entonces la red total se vuelve tetragonal. La distorsión uniaxial puede ocurrir más fácilmente que la expansión isotrópica, de tal manera que la estructura BCC puede acomodar más fácilmente el átomo intersticial dentro del octaedro que dentro de las cavidades tetraédricas con sus vecinos equidistantes. TRANSFORMACIONES DIFUSIVAS POR PRECIPITACIÓN L b b A B b A b B 18 13/12/2014 TRANSFORMACIONES DIFUSIVAS POR PRECIPITACIÓN ASPECTOS HISTÓRICOS MÉTODO DE ENDURECIMIENTO DEL METAL (Edad de Bronce – 1903) ► Endurecimiento por Acritud ► Endurecimiento por Soluto - Debido a los conocimientos Ancestrales se sabia el cómo, más no el por qué - FILOSOFÍA DEL DISEÑO DE ALEACIONES FILOSOFÍA HEURÍSTICA: Arte “Si un poquito es bueno, añada más hasta que algo malo pase” Se desarrollaron una multitud de reglas heurísticas relacionando a las variables composición y procesamiento con las propiedades Un ingrediente clave en el diseño de aleaciones es la manipulación de dos elementos críticos: Comp. Química y Microestructura 19 13/12/2014 FILOSOFÍA DEL DISEÑO DE ALEACIONES La metalurgia para ese entonces seguía siendo eminentemente artesanal, fundamentada en el “ARTE” desarrollado por la experiencia y el descubrimiento empírico. Los metales eran manufacturados y transformados según recetas empíricas generalmente secretas y muy similares a los procedimientos de los alquimistas de la edad media. Por un largo tiempo la metalurgia clásica permaneció una ciencia descriptiva. Se sabía que si uno añadía este o aquel elemento a una aleación sus propiedades serían afectadas. De la misma manera se sabia que calentando o enfriando o martillando (forjando) el metal cambiaba su comportamiento mecánico. Todavía no existe una teoría científica para diseñar aleaciones que permita a la industria del aluminio diseñar, interpretar y predecir las diferentes propiedades de interés metalúrgico basándose solo en sus principios y postulados. TEORÍA DEL ENDURECIMIENTO POR ACRITUD 1934 -TEORÍA DE LAS DISLOCACIONES M. Polanyi, E. Orowan y G. Taylor Egon Orowan (1901 – 1989) Explica las deformaciones plástica pero era un concepto invisible e imposible de ver al igual que los precipitados endurecedores del Duraluminio. 20 13/12/2014 TEORÍA DE LAS DISLOCACIONES CRISTAL I CRISTAL II TEORÍA DE LAS DISLOCACIONES Campo de esfuerzo o distorsión local. 21 13/12/2014 TEORÍA DE LAS DISLOCACIONES Dislocación de borde CAMPO DE ESFUERZO HIDROSTÁTICO DE UNA DISLOCACIÓN Nivel Esfuerzo Dislocación de borde 22 13/12/2014 APLICACIÓN DEL MICROSCOPIO ELECTRÓNICO DE TRANSMISIÓN (Resolución máxima 1 Å = 0.1 nm) OBSERVACIÓN DIRECTA DE DISLOCACIONES MEDIANTE IMAGENES TEM 1955 – PRIMERAS IMÁGENES DE DISLOCACIONES Peter Hirsch (16 Enero 1925) Laboratorio de Cavendish, Cambridge, 23 13/12/2014 EVIDENCIAS IRREFUTABLES MEDIANTE IMAGENES TEM 1955 - DISLOCACIÓN DE BORDE DENTRO DE LA RED CRISTALINA Jim Menter (1921 – 2006) ftalocianina de Platino EVIDENCIAS IRREFUTABLES MEDIANTE IMAGENES TEM 1955 - DISLOCACIÓN DE BORDE DENTRO DE LA RED CRISTALINA Jim Menter (1921 – 2006) ftalocianina de Platino 24 13/12/2014 EVIDENCIAS IRREFUTABLES MEDIANTE IMAGENES TEM 1955 – PRIMERAS IMÁGENES DE DISLOCACIONES EVIDENCIAS IRREFUTABLES MEDIANTE IMAGENES TEM 1955 – PRIMERAS IMÁGENES DE DISLOCACIONES 25 13/12/2014 DISLOCACIÓN DE BORDE ILUSTRADA EN UN CACTUS DISLOCACIÓN DE BORDE ILUSTRADA EN UNA MAZORCA 26 13/12/2014 DISLOCACIÓN DE BORDE ILUSTRADA EN UNA PARED DISLOCACIÓN DE TORNILLO ILUSTRADA EN UNA PARED 27 13/12/2014 DESPLAZAMIENTO DE UNA DISLOCACIÓN DE BORDE Plano extra de átomos Dirección del deslizamiento Dislocación ha deslizado dos planos hacia la derecha Nótese la distorsión alrededor de la línea dislocación ¿Dislocar o fracturar? Átomos más cerca que lo normal DESPLAZAMIENTO DE UNA DISLOCACIÓN DE BORDE 28 13/12/2014 DESPLAZAMIENTO DE UNA DISLOCACIÓN DE BORDE ¿Por qué es más fácil deformar un material con dislocaciones? Desplazar la dislocación requiere menos energía que desplazar todo el bloque DESPLAZAMIENTO DE UNA DISLOCACIÓN DE BORDE La deformación es un proceso localizado y la energía requerida es mucho menor 29 13/12/2014 DENSIDAD DE DISLOCACIONES DENSIDAD DE DISLOCACIONES ALTAMENTE DEFORMADO RECOCIDO r = 104 - 10 8 cm-2 r = 1012 cm -2 30 13/12/2014 DISTORSIONES DE LA RED CRISTALINA ¿REFUERZO O DEBILITAMIENTO DE LA ESTRUCTURA CRISTALINA? ESTRUCTURA DE UN METAL PURO IDEAL Red espacial interrumpida solo por los LG Red cristalina libre de defectos y distorsiones (Es muy blanda y elástica, poca resistencia). 31 13/12/2014 ANALOGÍA MECÁNICA DE LA ESTRUCTURA CRISTALINA Red en estado estable, no tensionada, flexible. Los resortes conectan átomos. ANALOGÍA DE LA ESTRUCTURA CRISTALINA ANALOGÍA Las cuerdas deben ser fuertemente tensadas para poder golpear la pelota (Implica entonces una estructura muy rígida, altamente resistente y muy dura) 32 13/12/2014 ANALOGÍA DE LA ESTRUCTURA CRISTALINA ANALOGÍA Red de la raqueta muy floja (cuerdas no tensadas) la pelota es retenida por la malla (Estructura muy blanda y elástica) DISLOCACIONES Y ENDURECIMIENTO POR TRABAJO Metales son dúctiles y tenaces debido a que las dislocaciones pueden moverse a través de la red cristalina con relativa facilidad. 33 13/12/2014 Esfuerzo verdadero FENÓMENO DE ACRITUD Endurecimiento por trabajo (ACRITUD) Trabajo en frío Deformación verdadera RESISTENCIA DENSIDAD DE DISLOCACIONES EXPERIMENTO EN EL AULA 34