Modelado y Simulación de una Caldera Convencional

Modelado y Simulación de una Caldera Convencional
AUTOR:
DIRECTOR:
Jordi Peñalba Galán
F.Javier Calvente Calvo
Septiembre / 2004
Índice
_________________________________________________________________________
1
Índice
1.- Índice
2.-Objeto del Proyecto
3.- Antecedentes
4.- Descripción de la Caldera
4.1.- Lista de Acrónimos
4.2.- Descripción Básica
4.3.- Partes de una Caldera
4.3.1.- Calderín
4.3.2.- Zona de Radiación
4.3.3.- Zona de Convección
4.3.3.1.- Down-Comer
4.3.3.2.- Recalentador
4.3.3.3.- Precalentador de Aire
4.4.- Funcionamiento de una Caldera
4.4.1.- Circuito de Agua
4.4.2.- Circuito de Humos
5.- Diseño del Modelo Matemático
5.1.- Modelo Matemático del Calderín
5.1.1.- Balance de Materia del Calderín
5.1.2.- Balance de Energía del Calderín
5.1.2.1.- Simplificaciones
5.1.2.2.- Entalpía del Agua de Alimentación
5.1.2.3.- Temperatura del Calderín
5.2.- Modelo Matemático de la Zona de Combustión
5.2.1.-Balance de Materia de la Zona de Combustión
5.2.2.-Balance de Energía de la Zona de Combustión
5.3.- Modelo Matemático del Recalentador
5.3.1.- Balance de Materia del Recalentador
5.3.2.- Balance de Energía del Recalentador
5.4.- Modelo Matemático del Precalentador de Aire
5.4.2.- Balance de Energía del Precalentador de Aire
5.5.- Modelo Matemático del Colector de Vapor
2
Índice
_________________________________________________________________________
6.- Control y Simulación del Modelo
6.1.- Control de la Caldera
6.1.1.- Control de Combustión
6.1.1.1.- Balance de Energía
6.1.1.2.- Control del Hogar
6.1.1.3.- Control Antihumo(Selectores Cruzados)
6.1.1.4.- Tiro Forzado
6.1.1.5.- Control del Ratio
6.1.2.- Control del Agua de Alimentación
6.1.2.1.- Control de Elemento Simple
6.1.3.- Control de la Temperatura del Vapor
6.1.3.1.- Control de Elemento Simple
6.2.- Ajuste de los Controladores
6.2.1.- Ajuste del Control de Caudal de GN
6.2.2.- Ajuste del Resto de Controladores
6.3.- Simulación de la caldera
6.3.1.- Calderín
6.3.1.1.- Balance de Materia
6.3.1.2.- Control de Nivel
6.3.1.3.- Balance de Energía
6.3.2.- Combustión
6.3.2.1.- Balance de Materia
6.3.2.2.- Balance de Energía Entrada
6.3.2.3.- Balance de Energía Salida
6.3.2.4.- Cálculo de O2 y N2 Necesario
6.3.2.5.- Temperatura de Gases
6.3.3.- Recalentador
6.3.3.1.- Recalentador Primario
6.3.3.2.- Recalentador Secundario
6.3.3.3.- Control Atemperador
6.3.4.- Precalentador de Aire
6.3.5.- Control de GN
6.3.6.- Control de Aire
6.3.7.- Control de Ratio
3
Índice
_________________________________________________________________________
6.3.8.- Control de la Caldera
6.3.9.- Control del Colector de Vapor
6.3.10.- Esquema General de la Caldera
7.- Resultados Obtenidos
7.1.- Condiciones Iniciales
7.2.- Consumos en el Colector de Vapor
7.2.1.- Nivel del Calderín
7.2.2.- Presión del Calderín
7.2.3.- Temperatura del Calderín
7.2.4.- Caudal de GN a la Caldera
7.2.5.- Caudal de Aire a la Caldera
7.2.6. Temperatura de Aire a la Caldera
7.2.7.- Presión del Colector de Vapor
7.2.8.- Temperatura del Vapor de Salida de la Caldera
7.2.9.- Consumo del Colector de Vapor
7.3.- Variaciones en el SP de O2
7.3.1.- Caudal de Aire
7.3.2.- Caudal de GN
7.4.- Conclusiones
7.5.- Agradecimientos
8.- Anexo
8.1.- Instrucciones de Matlab para la Generación de las Gráficas
9.- Referencias y Bibliografía
4
Objeto del proyecto
_________________________________________________________________________
2
Objeto del Proyecto
El objetivo final de este proyecto es obtener el modelo matemático de una Caldera de
Vapor Convencional y posteriormente utilizar dicho modelo para simular el
comportamiento del sistema y observar su dinámica.
Para conseguir este objetivo final se han marcado unas pautas de desarrollo:
1.- Descripción de la caldera de vapor y de los elementos que la componen.
2.- Desarrollo de un modelo matemático dinámico.
3.- Diseño del sistema de control.
4.- Simulación a través del programa Matlab y Simulink.
5.- Estudio del comportamiento del sistema.
5
Antecedentes
_________________________________________________________________________
3
Antecedentes
Una caldera de vapor es una unidad de proceso de gran importancia presente en todo
tipo de industrias. Las necesidades de vapor de agua en una industria son esenciales y
pueden resumirse en:
•
Vapor para turbinas que, acopladas a bombas y compresores, participan en un
ahorro eléctrico importante.
•
Vapor para el intercambio de calor en calentadores de fluidos.
•
Vapor como materia prima.
•
Vapor como medio de obtención de energía eléctrica.
Controlar de forma efectiva las condiciones de operación de una caldera es una
necesidad obvia, si se tiene en cuenta que, las elevadas presiones y temperaturas de
trabajo son las principales responsables de los problemas de peligrosidad, por riesgo de
explosiones. Tampoco debe olvidarse el aspecto económico, considerando no sólo los
costes de construcción, sino también los elevados costes de operación y de
mantenimiento, relacionados con las condiciones de operación mencionadas.
La búsqueda de esas condiciones óptimas de operación y control de las mismas no es
una tarea fácil, ya que una caldera de vapor es un sistema muy complejo, en el que
todas las variables están interrelacionadas. Además, la realización de pruebas de forma
directa sobre una caldera es difícil de llevar a cabo, tanto desde el punto de vista
técnico, por los peligros derivados de la manipulación de las condiciones de operación,
como económico (tiempo y dinero necesario).
Teniendo en cuenta esto, es necesario buscar un método alternativo de análisis: la
simulación.
La simulación es la representación del comportamiento de un proceso real mediante la
resolución de un modelo matemático. Las ventajas que presenta la utilización de
modelos matemáticos se resumen en:
•
Se puede analizar un proceso en profundidad, determinando qué variables o
parámetros son críticos e influyen de manera decisiva en el funcionamiento del
sistema global.
•
Se facilita enormemente la búsqueda de las condiciones óptimas de operación.
6
Antecedentes
_________________________________________________________________________
•
Se pueden estudiar de una forma segura condiciones límite, muy alejadas de las
normales de operación para analizar sus consecuencias.
•
Se puede utilizar como finalidad didáctica para el entrenamiento de operarios.
7
Descripción de la Caldera
_________________________________________________________________________
4
Descripción de la Caldera
4.1
Lista de Acrónimos
A lo largo de la memoria se ha utilizado una nomenclatura especial para definir cada una
de las partes de la caldera, líneas de producción y diferentes tipos de controles. Para
facilitar la compresión, a continuación se describe el significado de cada una de las siglas.
LINEAS DE PRODUCCIÓN
BFWH (BOILER FEED WATER HIGH): Agua de alta presión de alimentación a la
caldera.
SH (STEAM HIGH): Vapor de alta presión.
GN : Gas Natural
VÁLVULAS
LCV (LEVEL CONTROL VALUE): Válvula de control de nivel.
FCV (FLOW CONTROL VALUE): Válvula de control de caudal.
TCV (TEMPERATURE CONTROL VALUE): Válvula de control de temperatura.
CONTROLES
SP (SET POINT): Punto de consigna de la variable a controlar.
PV (POINT VALUE): Punto de la variable a controlar.
OP (OPERATION POINT): Punto de operación.
LC (LEVEL CONTROL): Controlador de nivel.
LX : Selector de nivel.
LT : Transmisor de nivel.
FC (FLOW CONTROL): Controlador de caudal.
FX : Selector de caudal.
FT : Transmisor de caudal.
TC (TEMPERATURE CONTROL): Controlador de temperatura.
TX : Selector de temperatura.
TT : Transmisor de temperatura.
PC (PRESSURE CONTROL): Controlador de presión.
PX : Selector de presión.
PT : Transmisor de presión.
8
Descripción de la Caldera
_________________________________________________________________________
4.2
Descripción Básica
Una caldera de vapor es un recipiente estanco en el que el agua a presión es
transformada en vapor , mediante la aplicación del calor resultante de la combustión de
gases, líquidos o sólidos combustibles.
Una caldera está diseñada para obtener el máximo calor creado del proceso de
combustión. Las características y diseño de cada una de ellas es muy variado en
función de la calidad-cantidad del vapor a obtener.
Las condiciones que pueden observarse en una caldera oscilan desde presiones de 10
kg/cm2 y 120 ºC hasta 280 kg/cm2 con vapor recalentado hasta 540 ºC.
Por la gran variedad de calderas de generación de vapor, pueden realizarse distintos
tipos de clasificaciones:
Por la naturaleza del servicio pueden ser: fija, portátil, locomotora o marina.
Por el tipo de combustible: calderas de carbón, combustibles líquidos, combustibles
gaseosos, mixtos y combustibles especiales (residuos, licor negro, cáscaras de
frutos,...).
Por el tiro: Tiro natural o tiro forzado (con hogar en sobrepresión, en depresión o en
equilibrio.
Por los sistemas de apoyo: calderas apoyadas o suspendidas.
Por la transmisión de calor: calderas de convección, calderas de radiación, calderas de
radiación-convección.
Por la disposición de los fluidos: calderas de tubos de agua (acuatubulares) y caldera de
tubos de humos (pirotubulares).
La caldera que se va a simular en el proyecto es una caldera fija, de combustible
gaseoso, de tiro forzado con el hogar en sobrepresión, apoyada en el suelo, con
transmisión de calor a través de convección y radiación, y de tipo acuotubular.
En las calderas acuotubulares, el agua circula por el interior de los tubos y los
productos de la combustión por el exterior de los mismos.
Este tipo de calderas es el utilizado para elevadas producciones y para vapor de alta
presión. Según los parámetros de caudal-presión-temperatura se diseña cada una de
ellas, siendo por dicho motivo muy variados los tipos y diseños.
Para pasar el agua desde la fase líquida a vapor, es necesario añadir calor con el fin de
aumentar la temperatura hasta su punto de ebullición. Este calor que eleva la
9
Descripción de la Caldera
_________________________________________________________________________
temperatura del agua se conoce como calor sensible. La temperatura de ebullición del
agua es de 100 ºC a presión atmosférica, aumentando cuando la presión aumenta y
viceversa. La temperatura de ebullición del agua se conoce también como temperatura
de saturación del vapor producido. Las relaciones entre la temperatura de saturación y
presión son propiedades termodinámicas fijas de vapor.
Cuando empieza la conversión del agua a vapor, la temperatura se mantiene constante,
aunque se siga añadiendo calor. El fluido se encuentra a las condiciones de saturación
presión/temperatura durante toda la conversión de agua a vapor. El calor que añade
durante el periodo de conversión del agua a vapor se conoce como calor latente de
vaporización.
La cantidad de calor total suministrado al vapor incluye el calor sensible y el calor
latente de vaporización. Generalmente, cuando la presión del vapor saturado aumenta,
la cantidad necesaria de calor sensible aumenta y la cantidad de calor latente
disminuye.
Añadiendo calor sensible adicional al vapor saturado, aumenta la temperatura por
encima de la correspondiente a la de saturación. El vapor que se obtiene por encima de
la temperatura de saturación se conoce con el nombre de vapor recalentado. El
recalentamiento aumenta la entalpía del vapor, o lo que es igual, su calor total. El
recalentamiento también produce la expansión del vapor, aumentando su volumen
específico [1].
TEMPERATURA
LÍQUIDO
LÍQUIDO + VAPOR
VAPOR
395 ºC
VAPOR
RECALENTADO
40 kg/cm2
250 ºC
TEMPERATURA DE
SATURACIÓN
LÍQUIDO
SATURADO
VAPOR
SATURADO
VOLUMEN
ESPECÍFICO
Figura 1: Relación entre la temperatura y el volumen específico del agua a presión constante.
10
Descripción de la Caldera
_________________________________________________________________________
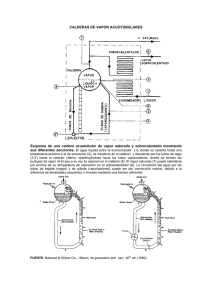
En un diagrama básico de una caldera pueden distinguirse dos sistemas independientes.
Uno de los sistemas está relacionado con el agua y vapor, mientras que el otro sistema
lo forma el conjunto de combustibles, aire y gases efluentes de la combustión. En el
primer sistema se introduce el agua, y después de recibir calor procedente del segundo,
se transforma en vapor, abandonando la caldera en forma de vapor de agua.
La combustión resultante del segundo sistema convierte la energía química del
combustible en energía calorífica, la cual se transfiere al agua en la Zona de Radiación.
Después los gases efluentes abandonan el hogar pasando a través de tubos de agua
situados en una zona donde estos tubos no pueden ver la llama, por lo que aquí el calor
se transfiere por convección.
Otro método de recuperar calor es la utilización de un precalentador de aire de
combustión. El aire pasa a través de este cambiador de calor antes de ser mezclado con
el combustible, y dado que la temperatura de los gases es superior a temperatura
ambiente, se transfiere una cantidad de calor que reduce las pérdidas de energía. El
calor añadido al aire pasa al hogar, reduciendo el combustible necesario en una
cantidad igual, en valor calorífico, al que ha sido transferido al aire. Aproximadamente
por cada 25ºC que se eleve la temperatura del aire, se ahorra un 1% de combustible.
El agua circula dentro de los tubos, los cuales están conectados entre dos o más
depósitos cilíndricos. En algunas calderas se reemplaza el depósito inferior por un
colector. El depósito superior se denomina calderín superior de vapor y se mantiene
aproximadamente con 50% de nivel de agua. El depósito inferior se mantiene lleno
completamente de agua, siendo el punto más bajo de la caldera. Este depósito se suele
conocer con el nombre de ‘Mud Drum’ por recoger los lodos que se forman en el
proceso de producción de vapor y que son drenados desde este punto [2].
11
Descripción de la Caldera
_________________________________________________________________________
BFWH
SH
CALDERÍN
Z. RADIACIÓN
BFWH
HUMOS
GN
AIRE
RISERS
R
E
C
A
L
E
N
T
A
D
O
R
SH
DOWN-COMER
BFWH
HUMOS
SH
Z. CONVECCIÓN
PRECALENTADOR
DE AIRE
SOPLANTE DE AIRE
COLECTOR DE VAPOR
DE ALTA PRESIÓN
CHIMENEA
Figura 2: Partes y funcionamiento de una caldera convencional.
12
BFWH PARA
ATEMPERADOR DEL
RECALENTADOR
Descripción de la Caldera
_________________________________________________________________________
4.3
Partes de una Caldera
4.3.1 Calderín
El calderín es un recipiente de configuración horizontal de mayor o menor espesor en
función del vapor producido. El tamaño del mismo será necesario para contener los
elementos de separación y admitir los posibles cambios de nivel según la carga.
La misión del calderín es acumular en la parte inferior el agua que es distribuida a los
distintos colectores de la cámara radiante, y a su vez separar en la parte alta el vapor de
las partículas de agua que lleva.
SH (VAPOR SATURADO)
CALDERÍN
VAPOR
BURBUJAS SALEN
BFWH
BURBUJAS SE CREAN
BURBUJAS CONDENSAN
AGUA
AGUA + VAPOR
AGUA
Figura 3: Funcionamiento del calderín.
4.3.2
Zona de Radiación
La Zona de Radiación es el lugar de la caldera donde se produce el calor necesario para
la generación de vapor, mediante la combustión del GN.
Esta parte de la caldera está formada por un haz de “tubos de subida” llamados Risers
situados de forma vertical, que se unen por la parte inferior con los tubos bajantes de
calderín (Down-Comer) y por la parte superior con el propio calderín.
Los Risers contienen en su interior agua + vapor, en cambio los Down-comer sólo
agua. La recirculación natural que existe entre los Down-comer y los Risers es debido a
la diferencia de densidad entre el agua y el vapor.
Esta zona recibe una temperatura aproximada de 1000ºC debido al calor provocado por
la llama directa y por los humos de la combustión.
Por el lado tubos pasa agua más vapor con una temperatura de salida variable, en
función del intercambio de calor y de la temperatura de entrada. A pesar de que es la
zona de mayor temperatura radiante, las paredes de los tubos están refrigerados por el
paso del agua, por esta razón es muy importante que el calderín siempre tenga nivel,
porque esto querrá decir que los tubos estarán inundados.
13
Descripción de la Caldera
_________________________________________________________________________
4.3.3 Zona de Convección
A diferencia de la zona anterior, en ésta los humos de la combustión son los que
calientan los tubos de agua o vapor. En ningún caso es la llama directa, quién aumenta
la temperatura del fluido de proceso.
La zona de convección normalmente está compuesta de varios elementos, como son los
down-comer, los recalentadores y los precalentadores de aire.
4.3.3.1 Down-Comer
Se llaman down-comer (“tubos de bajada”) a los tubos de agua que conectan el calderín
con la parte inferior de la zona de Radiación. Dicho de otra manera, son los tubos
bajantes del calderín. En esta zona el agua tiene un pequeño aumento de temperatura
antes de pasar a la zona de Radiación. Este incremento de temperatura se produce a
través de los humos de la combustión, que previamente ya vienen del intercambio
calorífico producido en el recalentador. Por tanto, estos humos realmente lo único que
hacen en esta zona es un precalentamiento del agua.
4.3.3.2 Recalentador
Es la sección de tubos que aprovecha el calor de los gases de escape para elevar la
temperatura del vapor generado por encima de la de saturación.
El vapor sobrecalentado aumenta el rendimiento del ciclo del vapor. En una turbina,
por cada 40ºC de incremento de temperatura sobre la de saturación, se obtiene un
aumento del 3% sobre el rendimiento.
El vapor sobrecalentado evita condensaciones en las tuberías y a la vez erosiones y
desequilibrios en los equipos.
El recalentador a simular es de tipo Convección-Radiación. El cual permite que la
temperatura de recalentamiento sea independiente de la carga de la caldera. También
hay que decir que está formado por dos subrecalentadores, entre los cuales hay una
pequeña inyección de agua a través de un atemperador para controlar la temperatura de
salida del recalentador.
14
Descripción de la Caldera
_________________________________________________________________________
4.3.3.3 Precalentador de Aire
Como ya se ha dicho en otra ocasión, el calentamiento del aire facilita y mejora el
rendimiento de la combustión.
En una caldera, después del paso de los humos a través de los down-comer, aún tiene
temperatura suficiente como para precalentar el aire hasta los 160ºC aproximadamente.
15
Descripción de la Caldera
_________________________________________________________________________
4.4
Funcionamiento de la Caldera
4.4.1
Circuito de Agua
El principio de funcionamiento de una caldera de vapor, tiene como fin evaporar agua
y sobrecalentar el vapor obtenido, mediante energía liberada en una reacción de
combustión. En concreto la caldera de vapor elegida para el modelado funciona de la
siguiente forma:
El agua de alimentación BFWH (Boiler Feed Water High) llega al calderín, y desde
allí, a través de los tubos bajantes (down-comer) llega hasta el colector inferior. Desde
este colector de distribución, el agua precalentada pasa a través de los tubos
alimentadores (risers), situados en las paredes del hogar de la caldera.
El vapor se genera en estos tubos (risers), recogiéndose después, en los colectores
superiores de las paredes laterales. El vapor generado pasa a continuación por los tubos
de descarga del calderín por dentro de un deflector circular. El vapor sale del deflector
circular y pasa por los separadores a la cámara de vapor, por encima del agua del
calderín. El agua separada del vapor condensa en el calderín.
Antes de que el vapor llegue a los tubos alimentadores del recalentador, debe pasar por
unos secadores, que están construidos de forma que el vapor tenga que chocar en una
serie de tabiques que le hacen cambiar de dirección. Esto elimina con efectividad los
restos de humedad del vapor.
El vapor saturado SH (Steam High) pasa al colector de entrada del recalentador que
consta de dos etapas (recalentador primario y recalentador secundario). A continuación,
el vapor pasa al colector general de vapor, desde donde se redistribuye a las diferentes
unidades del complejo químico.
La caldera, que se ha elegido para la simulación, produce vapor sobrecalentado a 40
kg/cm2 y 395 ºC, a partir de agua a 140 ºC (H = 589,20 kJ/kg)
[3]
y utilizando como
combustible el Gas Natural.
La caldera es de tipo acuotubular, es decir el agua circula por dentro de los tubos, con
una capacidad de producción de 70 T/h, a 40 kg/cm2 de presión y 395 ºC de
temperatura.
16
Descripción de la Caldera
_________________________________________________________________________
4.4.2
Circuito de Humos
El combustible que utiliza la caldera es el Gas Natural, donde teóricamente el 100% del
gas es metano CH4. La temperatura de entrada del combustible es de aproximadamente
25 ºC y el máximo caudal que puede aportar es de 12 T/h.
El aire aportado a la caldera para la combustión proviene del exterior con una
temperatura ambiente de 25 ºC. Antes de entrar en el hogar, el aire es calentado por un
Precalentador de Aire, gracias al intercambio de calor de los humos de la combustión
que salen de la caldera.
En el proceso de combustión de nuestra caldera sólo el 95 % de Gas Natural reacciona
con el aire, el otro 5 % no reacciona y se trata como parte del humo o gases de escape.
Del 95 % del Metano quemado, sólo el 80 % reaccionará para formar CO2 (dióxido de
carbono), el resto reaccionará para formar CO (monóxido de carbono).
CH4 + 2O2 == CO2 + 2H2O
CH4 + 3/2O2 == CO + 2H2O
A parte de los mencionados componentes, se considerarán también humos o gases de
escape el N2 (Nitrógeno), que no interviene en la combustión, el H2O (vapor de agua),
que se origina, y el exceso de O2 que no reacciona con el Gas Natural.
Los humos creados en la combustión llevan un calor, que será el responsable de los
diferentes intercambios que se irán produciendo en el hogar de la caldera y que
ayudarán a producir el vapor necesario según las necesidades.
Existen tres partes fundamentales dentro del hogar donde se producirán dichos
intercambios de calor: Zona de Radiación, Zona de Convección y Recalentador.
17
Diseño del Modelo Matemático
_________________________________________________________________________
5
Diseño del Modelo Matemático
El diseño de la caldera, descrita en los apartados anteriores, se ha conseguido a través
de la búsqueda de ecuaciones termodinámicas que interrelacionan las variables de
presión, temperatura, caudal, etc.
Para encontrar el modelo matemático, se ha dividido la caldera en varias partes,
estudiando cada caso por separado y aplicando balances de materia y de energía a las
variables de entrada y de salida de cada uno de los bloques. Luego, conectando cada
una de estas entradas y de salidas con el resto de bloques se ha conseguido cerrar el
modelo.
Las partes de la caldera estudiadas para el modelado han sido las siguientes:
Modelo Matemático del Calderín
Modelo Matemático de la Zona de Combustión
Modelo Matemático del Recalentador
Modelo Matemático del Precalentador de Aire
Modelo Matemático del Colector de Vapor
18
Diseño del Modelo Matemático
_________________________________________________________________________
5.1
Modelo Matemático del Calderín
Antes de plantear el modelo matemático del calderín, se deben tener en cuenta una
serie de suposiciones de trabajo para facilitar los cálculos.
Suposiciones:
Partimos del hecho de que la caldera siempre está en marcha, es decir, en el interior del
calderín siempre hay aproximadamente las mismas condiciones de temperatura, presión
y volumen.
El calderín tiene una capacidad máxima de 20m3 que correspondería con el 100% de
nivel.
Supondremos que en el calderín siempre existirá una mezcla bifásica de líquido
saturado y vapor saturado.
El caudal de salida de vapor saturado variará en función de la presión del colector de
vapor. Si disminuye la presión, aumenta la producción y viceversa.
En el calderín no hay partes móviles. No se realiza ningún trabajo (W=0).
Al calderín no hay un aporte directo de calor (Q=0).
Se considera que la energía potencial y energía cinética son nulas.
SH
BFWH
CALDERÍN
Q
DOWN-COMER
RISERS
Figura 4: Recirculación del agua Calderín, Down-Comer y Risers.
19
Diseño del Modelo Matemático
_________________________________________________________________________
El esquema de un sistema de caldeo se muestra en la figura 4. El calor Q suministrado
a los Risers produce una vaporización. Por la fuerza de la gravedad el vapor saturado
crea una recirculación en el circuito del Riser-calderín-Down-Comer. El agua de
alimentación BFWH se suministra al calderín y el vapor saturado SH sale del calderín
hacia el recalentador.
La presencia de vapor, bajo el nivel del calderín, provoca el fenómeno de la expansión–
contracción que dificulta el control de nivel. En realidad el sistema es mucho más
complicado que lo que aparece en la figura. El sistema tiene una geometría complicada,
ya que en realidad hay más Risers y Down-Comers que lo que aparece en la figura. La
salida de caudal de los Risers pasa a través de un separador de gotas, que separa el
vapor del agua. A pesar de la complejidad del sistema, se puede realizar un balance de
materia y energía de forma global.
Una propiedad de las calderas es la eficiente transferencia de calor gracias a la
vaporización y la condensación del vapor. Todas las partes del sistema que están en
contacto con el vapor-líquido saturado están en equilibrio térmico. La energía
almacenada en vapor y agua es liberada o absorbida muy rápidamente cuando la
presión varía. El mecanismo es la clave para entender la dinámica de la caldera. La
rápida liberación de energía asegura que diferentes partes de la caldera cambian su
temperatura de la misma forma. Por esta razón, la dinámica puede ser analizada por
modelos de bajo orden. La presión del calderín y la termodinámica pueden ser
representados muy bien con sistemas dinámicos de primer orden [8].
20
Diseño del Modelo Matemático
_________________________________________________________________________
5.1.1 Balance de Materia del Calderín
Partimos del hecho que el calderín tiene la entrada de agua de alimentación BFWH y la
salida de vapor saturado SH. Las dos variables se miden en toneladas por hora [T/h],
cosa que nos obliga a integrar su diferencia para conseguir la masa total que se está
almacenada en el calderín.
Mc = ∫ BFWH − SH
(1)
Mc es la masa total almacenada en el calderín.
Una vez tengo calculada la masa del calderín, tengo que encontrar el volumen
aplicando la siguiente fórmula:
Acumulación = Entrada - Salida
d
(ρ s ⋅Vst + ρ w ⋅Vwt ) = BFWH − SH
dt
(2)
donde:
Vst es el volumen que ocupa el vapor dentro del calderín, en m3.
Vwt es el volumen que ocupa el líquido dentro del calderín, en m3.
ρ w es la densidad específica del agua en estado líquido, en T/m3.
ρ s es la densidad específica del agua en estado vapor en T/m3.
Siendo
Vt = Vst + Vwt
(3)
el volumen total (40 m3), contando el calderín , los Risers y los Down-Comers.
Si sabemos que el calderín tiene una capacidad máxima de 20 m3, sabremos en cada
momento el volumen y el nivel del calderín.
d
(ρ s ⋅ Vt − ρ s ⋅Vwt + ρ w ⋅ Vwt ) = BFWH − SH
dt
(4)
Hay que tener en cuenta también las variaciones de densidad específica del agua y del
vapor en función de la presión. Estas variables serán tenidas en cuenta a través de la
siguiente expresión, encontrada a través de una hoja de cálculo:
 T 
ρ w  3  = 0.9768 − 9.0803 ⋅10 −3 ⋅ P + 1.134 ⋅10 − 4 ⋅ P 2
m 
21
(5)
Diseño del Modelo Matemático
_________________________________________________________________________
 T 
ρ s  3  = 7.21⋅10 −5 + 4.996 ⋅10 −4 ⋅ P + 3 ⋅10 −5 ⋅ P 2
m 
(6)
Una vez encuentro las densidades específicas del agua y del vapor en función de la
presión, busco el caudal que tengo en el calderín en m3.
(ρ w − ρ s ) dVwt
dt
= BFWH − SH
(7)
(ρ w − ρ s )Vwt = ∫ BFWH − SH
(ρ w − ρ s )Vwt = Mc
Vwt =
Mc
(ρ w − ρ s )
(8)
(9)
(10)
Ahora ya sólo debo encontrar el nivel sabiendo que el caudal máximo del calderín más
los Risers y los Down-Comer es de 40m3, y que el volumen sólo del calderín es de
20m3. Por tanto, la fórmula para calcular el nivel es:
NIVEL = 5[Vwt − 20]
(11)
5.1.2 Balance de Energía del Calderín
Para cerrar nuestro Balance de materia, estudiado anteriormente, debemos conocer en
cualquier momento la presión que tenemos en el calderín. Aunque en régimen
estacionario sabemos que la presión a la que trabaja el calderín es de 40 kg/cm2, en
cualquier momento puede sufrir una perturbación, ya sea de temperatura (calor), de
presión o de caudal, que haga que las condiciones varíen.
Para ello, escribiremos un balance de energía del calderín, en el que tendremos como
entrada el calor Q, que suministran los gases de escape de la caldera a los tubos risers y
a los tubos down-comers, y como salida la presión que tenemos en el calderín.
El balance global de energía es:
d
[ρ s ⋅ us ⋅ Vst + ρ w ⋅ u w ⋅ Vwt + mt ⋅ Cp ⋅ t m ] = Q + BFWH ⋅ h f − SH ⋅ hs
dt
Si la energía interna es u = h −
(12)
p
entonces:
ρ
d
[ρ s ⋅ hs ⋅Vst + ρ w ⋅ hw ⋅Vwt − pVt + mt ⋅ Cp ⋅ t m ] = Q + BFWH ⋅ h f − SH ⋅ hs
dt
22
(13)
Diseño del Modelo Matemático
_________________________________________________________________________
5.1.2.1
Simplificaciones
Podemos realizar simplificaciones adicionales si nos interesa saber la presión que hay
en el calderín. Para ello, multiplicaremos la ecuación del balance de materia (1) por hw
(entalpía del agua)(14), y posteriormente se lo restaremos a la ecuación (13) del
balance de energía.
d

hw ⋅  [ρ s ⋅Vst + ρ w ⋅ Vwt ] = hw ⋅ (BFWH − SH )
 dt

(14)
(13) - (14) = (15)
hc ⋅
d
(ρ s ⋅Vst ) + ρ s ⋅Vst ⋅ dhs + ρ w ⋅ Vwt ⋅ dhw − Vt ⋅ dp + mt ⋅ C p ⋅ dt s = Q − BFWH (hw − h f ) − SH ⋅ hc
dt
dt
dt
dt
dt
(15)
donde hc = hs − hw (entalpía de condensación).
De la ecuación anterior (15) se puede encontrar la relación que tiene la presión con los
demás términos, si consideramos que el nivel del calderín está bien controlado, las
variaciones de volumen serán pequeñas. Si despreciamos dichas variaciones (volumen
prácticamente constante), podemos llegar a la siguiente expresión:
K1 ⋅
dp
= Q − BFWH (hw − h f ) − SH ⋅ hc
dt
(16)
donde...
K1 = hc ⋅Vst ⋅
∂ρ s
∂h
∂h
∂t
+ ρ s ⋅Vst ⋅ s + ρ w ⋅Vwt ⋅ w + mt ⋅ C p ⋅ s − Vt
∂p
∂p
∂p
∂p
(17)
El fenómeno físico que domina en la dinámica de la presión de un calderín son el agua
y la masa del metal del calderín. Por tanto, una buena aproximación de K1 sería la
siguiente:
K1 ≈ ρ w ⋅Vwt ⋅
∂hw
∂t
+ mt ⋅ C p ⋅ s
∂p
∂p
(18)
Donde podemos hacer una aproximación de los siguientes términos, teniendo en cuenta
las características de nuestra caldera y habiéndola comparado con otras:
∂hw
= 980 kJ
(19)
∂p
∂t
mt ⋅ C p ⋅ s = 664 kJ
(20)
∂p
De las ecuaciones anteriores, todos los datos son conocidos menos las entalpías hs y
ρ w ⋅Vwt ⋅
hw que irán en función de la presión. Las operaciones se han realizado a través de
23
Diseño del Modelo Matemático
_________________________________________________________________________
tablas y una hoja de cálculo que nos ha dado una ecuación para cada entalpía en
función de la presión:
 kJ 
hw   = 0.2769 + 48.949 ⋅10 −3 ⋅ P − 7.054 ⋅10 −4 ⋅ P 2
T 
 kJ 
hs   = 2.6196 + 15.941⋅10 −3 ⋅ P − 2.806 ⋅10 −4 ⋅ P 2
T 
(21)
5.1.2.2 Entalpía del Agua de Alimentación
La entalpía del agua de alimentación hf se puede calcular sabiendo que, para un valor
aproximado de h, en estados de fase líquida, se puede calcular utilizando la siguiente
expresión:
h(T , p) ≈ uf (T ) + p ⋅ vf (T )
(22)
h(T , p) ≈ hf (T ) + vf (T ) ⋅ [ p − psat (T )]
(23)
Sabiendo que:
T es la temperatura del líquido (T = 140ºC).
Psat es la presión de saturación a la temperatura dada (Psat = 3.614 bar).
P es la presión del líquido (P = 70 bar).
hf es la entalpía del líquido a 140ºC (hf = 589.0 kJ/kg).
vf es el volumen específico a 140ºC (vf = 0.0010798m3/kg).
h(140º C ,70bar ) ≈ hf (140) + vf (140) ⋅ [ p − psat (140)]
(24)
kJ
m3
h(140º C ,70bar ) ≈ 589 + 0.0010798
⋅ [70bar − 3.614bar ]
kg
kg
kJ
h(140º C ,70bar ) ≈ 589.07
(25)
kg
h f ≈ 589.07
kJ
kg
(26)
5.1.2.3 Temperatura del Calderín
Para calcular la temperatura del calderín deberemos saber en cada momento la presión
del recipiente. Para ello, nos basaremos en los valores establecidos de presión y
temperatura saturados, introducidos previamente en una hoja de cálculo, consiguiendo
de este modo una ecuación.
La ecuación conseguida es :
24
Diseño del Modelo Matemático
_________________________________________________________________________
T = 103.67 ⋅ P 0.2392
5.2
(27)
Modelo Matemático de la Zona de Combustión
El modelado de la combustión se basa principalmente en la reacción entre el
combustible y el comburente, analizando su balance de materia, para conocer en todo
momento que cantidad de gases de escape se producen en la combustión, así como su
balance de energía para saber la cantidad de calor que se desprende.
Sabiendo que, el combustible es el Gas Natural con prácticamente 100 % de CH4
(Metano) en su composición, la reacciones que se producen son las siguientes.
CH4 + 2O2 == CO2 + 2H2O
CH4 + 3/2O2 == CO + 2H2O
Sólo el 95 % de CH4 reaccionará con el aire, el otro 5 % no reaccionará y se tratará
como parte del humo de salida. Del 95 % del CH4 quemado, sólo el 80 % reaccionará
para formar CO2 (dióxido de carbono), el resto reaccionará para formar CO (monóxido
de carbono) [3].
A parte de los mencionados componentes, se considerarán también humos o gases de
escape al N2 (Nitrógeno) que no interviene en la combustión, al H2O (vapor de agua)
que se origina y al O2 que no reacciona con el Gas Natural.
Las reacciones de combustión se llevan a cabo invariablemente con más aire del que se
necesita, para proporcionar oxígeno en proporción estequiométrica al combustible.
Los siguientes términos se utilizan comúnmente para describir las proporciones de
combustible y aire que alimentan un reactor, un horno o una caldera.
El oxígeno teórico es la velocidad de flujo molar continuo de oxígeno que se necesita
para efectuar la combustión completa del combustible, suponiendo que todo el carbono
del combustible se oxida para formar CO2 y todo el hidrógeno se oxida para formar
H2O.
El aire teórico es la cantidad de aire que contiene el oxígeno teórico.
El aire en exceso es la cantidad en exceso del aire que alimenta a la caldera con
respecto al aire teórico.
%Aire en exceso =
[Molesaire]ALIMENT . − [Molesaire]TEORICO ⋅100
[Molesaire]TEORICO
25
(28)
Diseño del Modelo Matemático
_________________________________________________________________________
5.2.1 Balance de Materia de la Zona de Combustión
A continuación se estudian los balances moleculares de cada uno de los componentes.
Sabemos que la entrada máxima de GN es de 12 T/h (750.000Mol/h) y de 220 T/h de
aire asegurando un exceso de aire del 3 %.
Componentes de ENTRADA:
O2 Alimentación. (Oxígeno real que entra en la caldera)
21T / h _ O2 10 6 gr / h _ O2 1mol / h _ O2
T / h _ Aire ⋅
= Mol / h _ O2
100T / h _ Aire 1T / h _ O2 32 gr / h _ O2
(29)
N2 Alimentación. (Nitrógeno real que entra en la caldera)
79T / h _ N 2 10 6 gr / h _ N 2 1mol / h _ N 2
T / h _ Aire ⋅
= Mol / h _ N 2
º
100T / h _ Aire 1T / h _ N 2 28 gr / h _ N 2
(30)
Componentes de SALIDA:
CH4 de Salida (Metano que no reacciona)
Mol / h _ CH 4 _ Entrada ⋅
5%CH 4
= Mol / h _ CH 4 _ Salida
100%CH 4
(31)
N2 de Salida
El N2 es un componente que no forma parte de la reacción y por tanto los mol/h de
salida son iguales a los de entrada.
CO de Salida:
Mol / h _ CH 4 ⋅
20%CH 4 1mol / h _ CO
⋅
= Mol / h _ CO
100%CH 4 1mol / h _ CH 4
(32)
H2O de Salida
Mol / h _ CH 4 ⋅
4Mol / h _ H
4 Mol / h _ H
2 Mol / h _ H
= Mol / h _ CH 4 ⋅
+ qMol _ H 2 O ⋅
1Mol / h _ CH 4
1Mol / h _ CH 4
1Mol / h _ H 2O
(33)
26
Diseño del Modelo Matemático
_________________________________________________________________________
CO2 de Salida
Mol / h _ CH 4 ⋅
1Mol / h _ C
1Mol / h _ C
1Mol / h _ C
= q1Mol / h _ CH 4 ⋅
+ q 2Mol / h _ CO ⋅
+
1Mol / h _ CO
1Mol / h _ CH 4
1Mol / h _ CH 4
+ q3Mol / h _ CO2 ⋅
1Mol / h _ C
1Mol / h _ CO2
q1 = Mol / hCH 4
q 2 = Mol / hCO
q3 = Mol / hCO2
(34)
O2 de Salida
Mol / h _ O2 ⋅
1Mol / h _ O
2Mol / h _ O
2Mol / h _ O
= q1Mol / h _ O2 ⋅
+ q 2 Mol / h _ CO ⋅
+
1Mol / h _ CO
1Mol / h _ O2
1Mol / h _ O2
+ q3Mol / h _ CO2 ⋅
2 Mol / h _ O
1Mol / h _ O
+ q 4 Mol / h _ H 2 O ⋅
1Mol / h _ CO2
1Mol / h _ H 2 O
q 2 = Mol / hCO
q3 = Mol / hCO2
q 4 = Mol / hH 2 O
q1 = Mol / hO2
(35)
En la siguiente tabla se observa de forma resumida el balance molecular de los
componentes de entrada y de salida de la reacción para los valores máximos de
producción:
Masa Molar
ENTRADA
SALIDA
CH4
16
O2
32
1.440.000 Mol/h 46,2 T/h
N2
28
6.210.000 Mol/h 173,8 T/h 6.210.000 Mol/h 173,8 T/h
CO2
44
562.500 Mol/h 24,75 T/h
CO
28
150.000 Mol/h
H2 O
18
750.000 Mol/h
12T/h
37.500 Mol/h
0,6 T/h
90.000 Mol/h
13,7 T/h
2,4 T/h
1.425.000 Mol/h 25,65 T/h
Tabla 1: Balance molecular de los componentes de entrada y de salida.
27
Diseño del Modelo Matemático
_________________________________________________________________________
5.2.2 Balance de Energía de la Zona de Combustión
A continuación se han calculado las entalpías de cada uno de los componentes que
intervienen en la reacción, teniendo en cuenta que la reacción se produce a una presión
suficientemente baja para que se considere que el gas, en este caso el metano, se
comporte idealmente.
Al realizar el cálculo de las entalpías hay que tener en cuenta las temperaturas de cada
uno de los componentes.
La temperatura del GN será de 25 ºC constante.
La temperatura del Aire variará en función del intercambio que exista en el
Precalentador de Aire, pero rondará los 165 ºC.
La temperatura de los gases de escape rondará los 1000 ºC.
Entalpías de ENTRADA:
Para el cálculo de las entalpías necesitamos saber la capacidad calorífica Cp de los
componentes de entrada, que se resume en la siguiente tabla:
a
b
CH4 34.31 5,469
c
d
T
0,3661 -11
25ºC
Cp=a+b10-2T+c10-5T2+d10-9T3
35,68 J/molºC
2,23kJ/kgºC
O2 29,1
1,158
-0,6076 1,311 175ºC 30,95 J/molºC
0,97kJ/kgºC
N2 29,0
0,2199 0,5723 -2,871 175ºC 29,54 J/molºC
1,06kJ/kgºC
Tabla 2: Capacidad calorífica de los componentes de entrada.
Una vez conocemos las Cp, prácticamente constante, calculamos a continuación las
entalpías de cada reactivo. Para ello utilizaremos la siguiente fórmula:
H = Cp ⋅ (T2 − T1 )
(36)
Sabemos que la entalpía del metano a 25 ºC es de –74,85 kJ/kg.
Cp
CH4 -
T1
-
T2
-
H
-74,85 kJ/kg
O2 0,97kJ/kgºC 25ºC 175ºC 145,5 kJ/kg
N2 1,06kJ/kgºC 25ºC 175ºC 159 kJ/kg
Tabla 3: Entalpía de los componentes de entrada.
28
Diseño del Modelo Matemático
_________________________________________________________________________
Si multiplico la entalpía de cada componente por el caudal en ese momento encontraré
el calor de entrada en MJ/h. La tabla la siguiente es orientativa por lo que hace
referencia a los valores, ya que el caudal de cada gas irá variando en cada instante, por
esto los valores que se reflejan a continuación son para el caso de producción máxima
H
Caudal
Q
CH4
-74,85 kJ/kg
12 T/h
-898,2 MJ/h
O2
145,5 kJ/kg
50,4 T/h
7.333,2 MJ/h
N2
159 kJ/kg
189,6 T/h
30.146,4 MJ/h
36.581,4 MJ/h
TOTAL
Tabla 4: Calor de los componentes de entrada.
Entalpías de SALIDA:
Para el cálculo de las entalpías necesitamos saber la capacidad calorífica Cp de los
componentes de entrada, que se resume en la siguiente tabla:
a
b
CH4 34.31 5,469
c
d
0,3661
-11
T
Cp=a+b10-2T+c10-5T2+d10-9T3
1000ºC 81,66 J/molºC
5,1 kJ/kgºC
O2
29,1
1,158 -0,6076 1,311 1000ºC 35,92 J/molºC
1,12 kJ/kgºC
N2
29,0 0,2199 0,5723 -2,871 1000ºC 34,05 J/molºC
1,22 kJ/kgºC
CO2 36,11 4,233
-2,887 7,464 1000ºC 57,03 J/molºC
1,3 kJ/kgºC
CO 28,95 0,411
0,3548 -2,22 1000ºC 34,39 J/molºC
1,23 kJ/kgºC
H2O 33,46 0,688
0,7604 -3,593 1000ºC 44,35 J/molºC
2,46 kJ/kgºC
Tabla 5: Capacidad calorífica de los componentes de salida.
29
Diseño del Modelo Matemático
_________________________________________________________________________
Una vez conocemos las Cp, prácticamente constante, calculamos a continuación las
entalpías de cada reactivo. Para ello utilizaremos la siguiente fórmula:
H = Cp ⋅ (T2 − T1 )
Cp
T1
(36)
T2
H
CH4 5,1 kJ/kgºC 25ºC 1000ºC 4972,5 kJ/kg
O2 1,12 kJ/kgºC 25ºC 1000ºC
1092 kJ/kg
1,22 kJ/kgºC 25ºC 1000ºC 1189,5 kJ/kg
N2
CO2 1,3 kJ/kgºC 25ºC 1000ºC 1267,5 kJ/kg
CO 1,23 kJ/kgºC 25ºC 1000ºC 1199,25 kJ/kg
H2O 2,46 kJ/kgºC 25ºC 1000ºC 2398,5 kJ/kg
Tabla 6: Entalpía de los componentes de salida.
Si multiplico la entalpía de cada componente por el caudal en ese momento, encontraré
el calor de entrada en MJ/h. Como ya se ha dicho anteriormente, estos valores son
orientativos, pues como ya sabemos variarán en función del caudal de cada uno de los
gases de escape.
H
Caudal
Q
CH4
4972,5 kJ/kg
0,6 T/h
2.983,5 MJ/h
O2
1092 kJ/kg
7,2 T/h
7.862,4 MJ/h
N2
1189,5 kJ/kg 189,6 T/h 225.529,2 MJ/h
CO2
1267,5 kJ/kg 24,75 T/h 31.370,6 MJ/h
CO
1199,25 kJ/kg
H2 O
2398,5 kJ/kg 25,65 T/h 61.521,5 MJ/h
2,4 T/h
2.878,2 MJ/h
332.145,4 MJ/h
TOTAL
Tabla 7: Calor de los componentes de salida.
Si al calor total de salida le restamos el de entrada encontramos el incremento de calor
que sufre la reacción. Balance de energía:
∆H =
∑
SALIDA
ni ⋅ H i −
∑n ⋅ H
i
ENTRADA
∆H = 332.145,4 − 36.581,4
∆H = 295.564MJ / h
30
i
(37)
Diseño del Modelo Matemático
_________________________________________________________________________
5.3
Modelo Matemático del Recalentador
Como ya se ha comentado en la descripción de la caldera, con el recalentador
conseguimos aumentar la temperatura del vapor saturado que sale del calderín
convirtiéndolo en vapor recalentado. Pasamos de tener aproximadamente 250 ºC a
tener 395 ºC a la salida. Este salto de temperatura sólo se consigue con un aporte extra
de calor que nos dejan los humos a su paso. Este intercambio termodinámico, entre el
humo y el vapor que pasa por los tubos, es la parte que hay que modelar en el
recalentador, y que a continuación estudiaremos [3].
5.3.1 Balance de Materia del Recalentador
Sabemos que este recalentador está formado por dos etapas asimétricas, entre las cuales
hay una inyección de agua BFWH para controlar la temperatura de salida del vapor
recalentado hacia el colector de vapor.
Dicha inyección de agua se debe sumar al vapor que sale de la primera etapa del
recalentador. El resultado será la cantidad total de vapor SH más agua BFWH que
entrará en la segunda etapa.
5.3.2 Balance de Energía del Recalentador
El Balance de Energía de la primera etapa del recalentador es igual a la segunda, por
eso sólo analizaremos una de ellas.
Primero calculamos la entalpía de cada uno de los componentes de los gases de escape.
Para ello, debo conocer la capacidad calorífica Cp de cada componente, y la
temperatura de entrada y de salida de los humos al pasar por la primera etapa del
recalentador.
H = Cp ⋅ (T1 − T2 )
(36)
La temperatura de entrada va en función de la cantidad de GN que se está quemando.
La temperatura de salida de los humos es fácil de calcular, porque se ha supuesto que
siempre hay un descenso de temperatura de 75 ºC entre la entrada y la salida.
31
Diseño del Modelo Matemático
_________________________________________________________________________
En la tabla siguiente se calculan las capacidades caloríficas Cp de cada componente.
a
b
c
d
CH4 34.31 5,469 0,3661
-11
T
Cp=a+b10-2T+c10-5T2+d10-9T3
800ºC 74,77 J/molºC
4,67 kJ/kgºC
O2
29,1
1,158 -0,6076 1,311 800ºC 35,15 J/molºC
1,10 kJ/kgºC
N2
29,0 0,2199 0,5723 -2,871 800ºC 32,95 J/molºC
1,18 kJ/kgºC
CO2 36,11 4,233
-2,887
7,464 800ºC 55,32 J/molºC
1,26 kJ/kgºC
CO 28,95 0,411 0,3548
-2,22 800ºC 33,37 J/molºC
1,19 kJ/kgºC
H2O 33,46 0,688 0,7604 -3,593 800ºC 41,99 J/molºC
2,23 kJ/kgºC
Tabla 8: Capacidad calorífica de los componentes de los gases de escape.
Luego calculamos la entalpía de cada gas:
Cp
T1
T2
H
CH4 4,67 kJ/kgºC 800ºC 725ºC 350,25 kJ/kg
O2 1,10 kJ/kgºC 800ºC 725ºC
82,5 kJ/kg
N2 1,18 kJ/kgºC 800ºC 725ºC
88,5 kJ/kg
CO2 1,26 kJ/kgºC 800ºC 725ºC
94,5 kJ/kg
CO 1,19 kJ/kgºC 800ºC 725ºC 89,25 kJ/kg
H2O 2,23 kJ/kgºC 800ºC 725ºC 167,25 kJ/kg
Tabla 9: Entalpía de los componentes de los gases de escape.
Si multiplico la entalpía de cada componente por el caudal en ese momento encontraré
el calor que dejan a su paso los humos y que es absorbido por el vapor que pasa por los
tubos del recalentador.
En la siguiente tabla se muestra el calor total, que es susceptible de variaciones en
función de la cantidad de humos.
H
Caudal
Q
CH4
350,25 kJ/kg
0,6 T/h
210,15 MJ/h
O2
82,5 kJ/kg
7,2 T/h
594 MJ/h
N2
88,5 kJ/kg
189,6 T/h 16.779,6 MJ/h
CO2
94,5 kJ/kg
24,75 T/h 2.338,8 MJ/h
CO
89,25 kJ/kg
H2 O
167,25 kJ/kg 25,65 T/h 4.289,9 MJ/h
2,4 T/h
214,2 MJ/h
24.426,6 MJ/h
TOTAL
Tabla 10: Calor que desprenden los gases de escape.
32
Diseño del Modelo Matemático
_________________________________________________________________________
Una vez conocemos el calor que absorbe el vapor, podemos calcular su temperatura a
la salida de la primera etapa del recalentador.
∆Q = m ⋅ Cp ⋅ ∆T
(38)
Donde:
∆Q es el calor absorbido por el vapor SH.
m es el caudal de vapor SH que pasa por el recalentador
Cp es la capacidad calorífica del vapor SH.
∆T es el incremento de temperatura del recalentador lado vapor. Del cual conocemos
T1 (entrada) y T2 (salida) es la temperatura a encontrar.
33
Diseño del Modelo Matemático
_________________________________________________________________________
5.4
Modelo Matemático del Precalentador de Aire
A diferencia del recalentador de vapor, al precalentador de aire no se le ha modelado
un Balance de Materia, porque el aire que entra es igual que sale. El único cambio
termodinámico que sufre es el intercambio de calor que hay entre los humos, que pasan
por la última parte del conducto de humos de la caldera, y el aire que pasa por los tubos
hacia la cámara de combustión.
5.4.1 Balance de Energía del Precalentador de Aire
Como en el caso anterior, primero calculamos el calor que dejarán los humos en el
precalentador de aire, y luego a través de este calor, que absorbe el aire para calentarse,
podemos calcular la temperatura de salida.
Por tanto, primero calculamos las capacidades caloríficas Cp de los gases de escape en
función de una temperatura media, que en este caso es 700 ºC.
a
b
c
CH4 34.31 5,469 0,3661
d
-11
T
Cp=a+b10-2T+c10-5T2+d10-9T3
700ºC 70,61 J/molºC
4,41 kJ/kgºC
O2
29,1
1,158 -0,6076 1,311 700ºC 34,68 J/molºC
1,08 kJ/kgºC
N2
29,0 0,2199 0,5723 -2,871 700ºC 32,36 J/molºC
1,16 kJ/kgºC
CO2 36,11 4,233
-2,887
7,464 700ºC 54,15 J/molºC
1,23 kJ/kgºC
CO 28,95 0,411 0,3548
-2,22 700ºC 32,80 J/molºC
1,17 kJ/kgºC
H2O 33,46 0,688 0,7604 -3,593 700ºC 40,77 J/molºC
2,26 kJ/kgºC
Tabla 11: Capacidad calorífica de los componentes de los gases de escape.
34
Diseño del Modelo Matemático
_________________________________________________________________________
Ahora calculamos la entalpía de cada componente en función de las capacidades
caloríficas Cp calculadas, y sabiendo que la temperatura de entrada media es 700 ºC y
que entre la entrada y la salida de humos existe una diferencia de aproximadamente
100 ºC. De forma que la temperatura de salida de los humos de esta caldera ronda los
600 ºC.
Cp
T1
T2
H
CH4 4,41 kJ/kgºC 700ºC 600ºC 441 kJ/kg
O2 1,08 kJ/kgºC 700ºC 600ºC 108 kJ/kg
N2
1,16 kJ/kgºC 700ºC 600ºC 116 kJ/kg
CO2 1,23 kJ/kgºC 700ºC 600ºC 123 kJ/kg
CO 1,17 kJ/kgºC 700ºC 600ºC 117 kJ/kg
H2O 2,26 kJ/kgºC 700ºC 600ºC 226 kJ/kg
Tabla 12: Entalpía de los componentes de los gases de escape.
Por último, multiplicando la entalpía de cada gas por el caudal conseguimos el calor
total que desprende el humo al pasar por el precalentador de aire, y que por otro lado,
absorbe el aire calentándose.
H
Caudal
Q
CH4
441 kJ/kg
0,6 T/h
264,6 MJ/h
O2
108 kJ/kg
7,2 T/h
777,6 MJ/h
N2
116 kJ/kg 189,6 T/h 21.993,6 MJ/h
CO2
123 kJ/kg 24,75 T/h 3.044,2 MJ/h
CO
117 kJ/kg
H2 O
226 kJ/kg 25,65 T/h 5.796,9 MJ/h
2,4 T/h
280,8 MJ/h
32.157,7 MJ/h
TOTAL
Tabla 13: Calor que desprenden los gases de escape.
La temperatura de salida del aire del precalentador irá en función del calor que en cada
momento variará en función del caudal de los humos. También dependerá del caudal de
aire que pase de su capacidad calorífica y de su temperatura de entrada (25 ºC).
∆Q = m ⋅ Cp ⋅ ∆T
35
(38)
Diseño del Modelo Matemático
_________________________________________________________________________
Donde:
∆Q es el calor absorbido por el Aire.
m es el caudal de Aire que pasa por el precalentador
Cp es la capacidad calorífica del Aire.
∆T es el incremento de temperatura del precalentador lado Aire.
36
Diseño del Modelo Matemático
_________________________________________________________________________
5.5
Modelo Matemático del Colector de Vapor
El colector de vapor se ha simulado como si fuera un gran depósito a una presión
determinada PCOL.
Nuestra caldera será el único aporte que habrá en el colector.
La caldera producirá vapor bajo demanda, en función de la diferencia de presión que
exista entre el calderín y el colector de vapor.
El colector de vapor tiene una entrada de SH, que será lo producido por nuestra
caldera, y una salida llamada SHCOL, que será el consumo de otros clientes de este
colector de vapor.
El colector de vapor se ha modelado de la siguiente forma:
PCOL = ∫
45
0
 T

C = 25 
2
 kg / cm 
1
(SH − SHCOL )dt
C
(39)
Donde C es la capacidad del colector que se ha calculado de forma empírica, a través
de la simulación.
37
Control y Simulación del Modelo
_________________________________________________________________________
6
Control y Simulación del Modelo
6.1
Control de la Caldera
Una vez vistos los aspectos fundamentales de una caldera de vapor, podemos pasar a
ver distintos sistemas de control que se llevan a cabo en una caldera [6].
Básicamente existen tres grupos que se pueden denominar como
Control de combustión.
Control de agua de alimentación.
Control de la temperatura de vapor.
6.1.1 Control de Combustión.
El término control de combustión se refiere a la parte del sistema de control de calderas
que lleva a cabo las dos funciones básicas siguientes:
Balance de energía.
Control del hogar.
Ambas están relacionadas entre sí, puesto que el control del hogar depende del balance
de energía. Estas dos partes del control de combustión serán tratadas de forma separada
para describir sus diferentes funciones.
6.1.1.1 Balance de Energía
En un proceso generador de vapor existe una demanda de energía de salida, en función
de la carga, que debe ser compensada por la energía de entrada suministrada por el
combustible. El sistema de balance de energía tiene en cuenta, tanto la de entrada como
la correspondiente a la salida, manipulando la energía de entrada a través del sistema
de control del hogar. El método más simple es el de controlar la presión de vapor
manipulando el combustible. La presión es proporcional a la carga, es decir, la
producción de vapor, representa la energía de salida, mientras que el caudal de
combustible representa la energía de entrada.
38
Control y Simulación del Modelo
_________________________________________________________________________
PV
SP
PV
PT
PC
ENERGÍA
DEMANDADA
SP
GN CONSUMIDO
FC
COLECTOR DE VAPOR
A VÁLVULA DE GN
Figura 5: Control de la presión del colector de vapor a partir del combustible.
Cuando los cambios en la demanda de vapor son frecuentes o relativamente rápidos,
puede utilizarse un sistema de adelanto, incluyendo la correspondiente compensación
dinámica, para evitar perturbaciones. La señal que se puede disponer como indicación
de la demanda del proceso, es la medida de caudal de vapor.
39
Control y Simulación del Modelo
_________________________________________________________________________
6.1.1.2 Control del Hogar
En respuesta a la demanda establecida por el balance de energía, el control del hogar
donde se lleva a cabo la combustión debe realizar las siguientes funciones:
Mantener la energía de entrada al nivel demandado por el balance.
Mantener la relación aire/combustible.
Mantener equilibrado el conjunto tiro forzado tiro inducido.
Mantener la caldera en condiciones de operación seguras.
Con respecto a la energía de entrada, ya se ha descrito anteriormente que ésta depende
de la energía de salida, y se manipula por medio del controlador de presión actuando
sobre combustibles utilizados en cada caso en particular.
Hasta aquí no se ha tenido en cuenta el aporte de aire necesario para la combustión, ni
por su puesto se control. Desde un punto de vista simple, el sistema de control de aire
se reduce a manejar en paralelo los controladores de combustible y aire.
PV
SP
PV
PT
PC
ENERGÍA
DEMANDADA
SP
GN CONSUMIDO
FC
MEDIDA DE PRESION
DEL VAPOR
RATIO
FX
A VÁLVULA DE AIRE
X
Figura 6: Control de la presión del colector de vapor a partir del combustible y del aire.
Con este sistema, a cada cantidad de energía demandada corresponde una cantidad de
aire establecida por la relación aire/combustible teniendo la ventaja de ser simple,
económico y rápido de respuesta. El principal inconveniente radica en que la relación
entre el aire y la energía demandada no es una variable medida, dependiendo de
parámetros tales como las características del combustibles, variaciones de presión y
temperatura de combustible, condiciones atmosféricas, etc. Si estas condiciones no se
mantienen constantes, la relación aire/energía óptima variará significativamente.
Conviene mencionar que la salida del controlador de presión representa la energía
demandada en unidades de combustible equivalente al aire, por lo que al manipular por
la relación aire/combustible da como resultado unidades de aire.
40
Control y Simulación del Modelo
_________________________________________________________________________
La solución óptima de cualquier sistema de control se obtiene cuando la variable a
controlar se puede medir, o se puede obtener por procedimientos indirectos. En este
caso la medida indirecta será el contenido de oxígeno en los gases de la combustión.
Recordemos que la combustión estequiométrica se realiza cuando se combina
químicamente cada molécula de combustible con la cantidad equivalente de oxígeno.
En la práctica este tipo de combustión no se puede realizar debido a causas tales como
mezcla incorrecta entre ambos componentes, dilución de los productos de combustión
por los gases inertes como el nitrógeno, vapor de agua en la atmósfera,...
La combustión completa se realiza si se introduce un exceso de aire con respecto a la
cantidad de combustible que se está utilizando. Es necesario que el exceso de aire sea
óptimo, puesto que si no lo es se puede presentar alguna de las situaciones que se
describen a continuación.
Cuando se trabaja con demasiado exceso de aire, se está desaprovechando energía a
través de los gases que salen por la chimenea.
Cuando se trabaja con insuficiente exceso de aire, se produce una pérdida de calor
debido al combustible que no ha reaccionado (inquemados).
Cuando existen combustibles inquemados se tiene un cierto riesgo de explosión, como
consecuencia de la falta de oxígeno.
6.1.1.3 Control Antihumo (Selectores Cruzados)
Una vez llegados a este punto, veamos el control de combustión para una caldera por el
sistema conocido como límites cruzados, o también antihumo, debido a la
particularidad por la que el aire suministrado a la combustión se introduce siempre
antes que el combustible, operando con exceso de aire durante los cambios de carga.
Este sistema es equivalente al anterior desde el punto de vista conceptual, al operar en
paralelo el aire y el combustible, sólo que en este caso se mejora con la inclusión del
sistema de selectores cruzados.
Consideramos primero el estado estacionario del sistema. Los controladores de
combustible y aire actúan para mantener sus medidas iguales a sus puntos de consigna.
Como consecuencia el sistema se encuentra en equilibrio entre el aporte y la demanda.
Al aumentar la demanda de vapor disminuye la presión y como el controlador de
presión tiene acción de control inversa, aumentará su salida para equilibrar el balance
de energía. Por último mencionar que la salida del multiplicador, sobre el que actúa la
41
Control y Simulación del Modelo
_________________________________________________________________________
relación combustible/aire, representa el caudal de combustible equivalente al aire
consumido en la combustión.
CAUDAL DE GN
CAUDAL DE AIRE
PRESION COLECTOR
FT
PT
FT
PV
SP
FX
RATIO
X
ENERGÍA
DEMANDADA
PV
PV
FC
SP
PX
PX
<
>
SEL. MIN
SP
FC
SEL. MAX
A VÁLVULA DE GN
A VÁLVULA DE AIRE
Figura 7: Control de la presión del colector de vapor a través de selectores cruzados.
Con este sistema no se controla realmente el caudal de aire, sino el de combustible
equivalente al aire. Esto es así porque los selectores han de comparar medidas dadas en
las mismas unidades de ingeniería, en este caso unidades de caudal de combustible. Por
eso se utiliza la relación combustible/aire, para que al multiplicar por el caudal de aire,
su salida venga dada en unidades de caudal de combustible equivalente al caudal de
aire, el cual sólo puede ser medido en el indicador situado a la salida del transmisor.
Veamos lo que ocurre cuando se produce un aumento o disminución de carga, o lo que
es igual, una disminución o aumento en la presión respectivamente.
INCREMENTO DE CARGA: En los primeros momentos disminuye la presión y su
controlador aumenta la salida mientras que los controladores de caudal de aire y
combustible permanecen igual. Al haber aumentado la señal de energía demandada, el
selector de mínima señal no la tomará en cuenta y dejará pasar la señal de caudal de
42
Control y Simulación del Modelo
_________________________________________________________________________
combustible equivalente al aire. El punto de consigna del controlador de combustible
sólo se moverá cuando lo haga el caudal de aire suministrado. Al mismo tiempo, el
selector de máxima tendrá en cuenta la señal de energía demandada, rechazando la del
combustible. Por tanto, el punto de consigna del aire seguirá a la demanda de carga. En
esta situación actúa el sistema de forma que el combustible sigue al aire.
DISMINUCIÓN DE CARGA: En los primeros momentos aumenta la presión y su
controlador disminuye la salida mientras que los controladores de caudal de aire y
combustible permanecen igual. Al haber disminuido la señal de energía demandada, el
selector de mínima acepta la correspondiente a la demanda, rechazando la del
combustible equivalente al aire, por lo que el punto de consigna del combustible se
hace igual a la demanda de energía, es decir, disminuye el caudal de combustible. El
selector de máxima sigue seleccionando la correspondiente al combustible y sólo se
modifica después de haberse modificado éste. En este caso el sistema actúa de forma
que el aire sigue el combustible.
Como puede verse, ante cambios en la carga, el caudal de aire actúa siempre de manera
que exista exceso de oxígeno. Por lo tanto, con este sistema de control se obtienen las
dos situaciones siguientes:
Ante un aumento de carga, el combustible no puede aumentar hasta que no ha
aumentado el caudal de aire.
Ante una disminución de carga, el aire no puede disminuir hasta que no ha disminuido
el caudal de combustible.
6.1.1.4 Tiro Forzado
El tiro forzado utiliza una soplante para proporcionar la cantidad de aire necesaria para
la combustión. Con esta soplante se crea en los conductos de aire una presión
ligeramente positiva, cuyo valor suele estar entre 25 y 50 mm de columna de agua,
controlada por el damper de tiro forzado.
Ante aumentos o disminuciones de carga, el comportamiento es el siguiente:
Incremento de carga. El punto de consigna del controlador de caudal aumenta por la
acción del sistema de control, abriendo el damper para dejar pasar más aire.
Disminución de carga. Al disminuir la demanda de aire, el comportamiento es
exactamente el mismo que el anterior, excepto que ahora el damper de aire cierra.
43
Control y Simulación del Modelo
_________________________________________________________________________
6.1.1.5 Control del Ratio
Necesitamos que en nuestra combustión siempre exista un exceso de oxígeno en humos
de salida, para asegurarnos de no producir inquemados.
El RATIO es GN/Aire. Es una variable que puede ir de 0,5 a 1.
RATIO =
GN
AIRE
(40)
Este valor se multiplicará por el valor real del aire que tengamos en ese momento, de
forma que variará la diferencia entre el SP del aire y la PV del aire.
Si aumentamos el RATIO aumentará la PV del aire, hecho que hará bajar la salida OP
a la válvula del aire y en consecuencia bajará la cantidad de aire a la caldera.
Si disminuimos el RATIO disminuirá la PV del aire, hecho que hará subir la salida OP
a la válvula del aire y en consecuencia aumentará la cantidad de aire a la caldera.
Como se observa en la figura la variable RATIO vendrá dada por la diferencia entre el
SP de % O2 (aproximadamente 3%) y el % O2 en humos.
CAUDAL DE AIRE
FT
%O2 EN HUMOS
SP DE %O2
RATIO
FX
0,5 - 1
X
PV
SP
FC
A VÁLVULA DE AIRE
Figura 8: Control del aire a partir del % de O2 en humos.
44
Control y Simulación del Modelo
_________________________________________________________________________
6.1.2 Control del Agua de Alimentación.
El agua entra en el calderín y, después de absorber en los tubos el calor de la
combustión, genera el vapor producido por la caldera. En una operación correcta, es
necesario que el nivel de agua se mantenga dentro de una banda alrededor del punto de
consigna del controlador. Una excesiva disminución del nivel puede dejar vacíos
algunos de los tubos de la caldera, los cuales serán sometidos a un sobrecalentamiento,
mientras que con un aumento excesivo en el nivel se puede llegar a la situación
peligrosa que salga del calderín agua junto con el vapor producido.
El nivel en el calderín es una medida del volumen de agua contenida en el mismo,
aunque existen algunas circunstancias que pueden falsear la medida, como veremos a
continuación. Para cada carga de la caldera hay un cierto volumen de agua que se
encuentra ocupado por burbujas de vapor. En los primeros momentos que siguen a un
incremento instantáneo de carga, sería de esperar una disminución del nivel en el
calderín. Sin embargo se da un proceso interesante de analizar, puesto que disminuye la
presión y, como consecuencia, se producen más burbujas, ocasionando un aumento en
el volumen de agua, haciendo aumentar el nivel cuando debería disminuir. Este
fenómeno se denomina hinchazón o expansión. Por el contrario, ante un aumento de la
presión por haber disminuido la carga, el nivel de agua tiende a contraer su volumen,
ocasionando el fenómeno de contracción.
Por último, el agua está siempre más fría que el vapor saturado, por lo que parte del
vapor producido en los tubos se condensa cuando entra en contacto con el agua en el
calderín. Un aumento rápido en el caudal de agua tiende a reducir temporalmente la
formación de burbujas en los tubos. Todas estas reacciones tienden a equilibrarse en
pocos segundos, pero en los primeros momentos responden en dirección inversa a la
correcta.
En base a todo lo anterior, el sistema de control de agua de alimentación necesita
responder rápidamente a los cambios de carga para mantener constante la cantidad de
agua almacenada.
45
Control y Simulación del Modelo
_________________________________________________________________________
6.1.2.1 Control de Elemento Simple
Este tipo de control se utiliza frecuentemente en calderas pequeñas con un gran
volumen de agua almacenada. Proporciona un control adecuado simple que las
variaciones de carga no sean muy importantes.
Tiene solamente una variable de proceso, el nivel en el calderín, para controlar el agua
de alimentación.
El transmisor de nivel proporciona la variable de proceso al controlador con acción
proporcional e integral. La salida de este controlador posiciona la válvula de entrada de
agua al calderín. Cuando se utiliza control de un elemento, los efectos de contracción y
expansión de volumen pueden ocasionar errores en el control.
VAPOR
CALDERÍN
LT
AGUA
Figura 9: Control del nivel del calderín.
46
PV
LC
SP
Control y Simulación del Modelo
_________________________________________________________________________
6.1.3 Control de la Temperatura del Vapor.
En muchas calderas existen recalentadores de vapor para aumentar su temperatura por
encima de la de saturación, lo cual se produce en el calderín. Nuestra caldera tiene dos
recalentadores denominados primario y secundario. Entre ambos recalentadores existe
un atemperador para disminuir la temperatura del vapor a la salida del primer
recalentador.
El atemperador inyecta agua a la línea de vapor, donde se vaporiza a su vez
mezclándose con el vapor recalentado, produciendo el enfriamiento de este último. El
grado de enfriamiento depende del el uso final del vapor.
6.1.3.1 Control de Elemento Simple
El sistema de control de elemento simple, como el que aparece en la figura, se utiliza
en calderas que no tienen grandes cambios de carga o lo hacen de forma muy lenta.
Este sistema tiene como variable de proceso la temperatura de salida del recalentador
secundario, fijando el operador el punto de consigna del controlador. La salida del
controlador posiciona la válvula de entrada del agua al atemperador.
ATEMPERADOR
VAPOR
RECALENTADOR
PRIMARIO
RECALENTADOR
SECUNDARIO
TC
CALDERÍN
AGUA
Figura 10: Control de la temperatura de salida de vapor.
47
Control y Simulación del Modelo
_________________________________________________________________________
6.2
Ajuste de los Controladores
El ajuste de los parámetros de los controladores PID de cada uno de los lazos de
control se ha realizado a través de las fórmulas denominadas de Ziegler-Nichols. Es un
método de aplicación práctica, que consiste en ir aumentando en saltos progresivos la
ganancia del controlador (provisto sólo de acción proporcional) hasta provocar en el
sistema una oscilación mantenida; esto es, hasta llevarlo a condición crítica. En este
momento se anota la ganancia Gu que presenta el controlador, y se mide el período de
la oscilación, llamado Pu. Entonces, los parámetros del controlador que
presumiblemente darán una respuesta temporal con una razón de amortiguación de ¼
(relación entre dos picos consecutivos), serán:
Para un controlador P:
P=
Gu
2
(41)
Para un controlador P+I:
P=
Gu
2,2
(42)
I=
1
1,2
=
Ti
Pu
(43)
P=
Gu
1,7
(44)
I=
1
2
=
Ti
Pu
(45)
Pu
8
(46)
Para un controlador P+I+D:
D = Td =
Cuanto menos, el método resulta útil como punto de partida, si bien, en muchas
ocasiones es preciso efectuar algunas correcciones para terminar de optimizar la
respuesta. En particular, el método no resulta satisfactorio en aquellos sistemas que
contengan algún componente del tipo integrador. Téngase presente que estas fórmulas
fueron desarrolladas para un determinado modelo de proceso y , por tanto, no son
realmente universales; pero, además, la optimización de un sistema variará según se
esté pensando en la respuesta a cambios en el SP o a perturbaciones.
Por otra parte, según el criterio elegido variarán los parámetros óptimos del
controlador. En otras palabras, la solución no es técnicamente única y puede depender
hasta de gustos o criterios personales. Por ejemplo, cuando una solución, con relación a
48
Control y Simulación del Modelo
_________________________________________________________________________
otra, disminuye ligeramente la amplitud de las oscilaciones a costa de hacerlas algo
más duraderas, y en ambos casos no se rebasa la limitación específica del proceso en
ninguno de los dos aspectos, entonces podríamos decir que ambas soluciones son
igualmente válidas [5].
6.2.1 Ajuste del Control de Caudal de GN
Como ejemplo del método de Ziegler-Nichols, mostraremos a continuación como se
han llegado a ajustar los parámetros del controlador del lazo de control, que gobierna el
caudal de GN a la caldera.
Figura 11: Control del caudal de GN.
Como se ve en la figura el controlador PID no tiene acción derivativa, ya que dicha
acción no suele emplearse en procesos rápidos, tales como un control de caudal, dado
que estos sistemas generan normalmente señales con un importante contenido de ruido
(variaciones rápidas que equivalen a altas frecuencias) el cual es amplificado por la
acción derivativa.
Para empezar el ajuste de parámetros, y siguiendo el método de Ziegler-Nichols,
haremos nula la constante integral Ti e iremos aumentando la constante G hasta que el
sistema se encuentre en el límite de la estabilidad, o dicho de otra manera, hasta que el
sistema tenga una respuesta de oscilación mantenida.
49
Control y Simulación del Modelo
_________________________________________________________________________
Haciendo una primera aproximación donde G = 0,01 y Ti = 0 (I = inf), nos
encontramos con la siguiente respuesta:
Gráfica 1: Respuesta del Caudal de GN ante variaciones del SP..
Si seguimos aumentando la ganancia del controlador llegamos a una situación crítica,
de amortiguación sostenida.
La respuesta encontrada tiene una amplitud de Gu = 0,5 y un periodo de Pu = 6*10-3.
Aplicando los cálculos del método para un controlador PI, encontramos los parámetros
proporcional e integral, tal y como se ve en los siguientes cálculos:
G=
Gu
5,5
=
= 2,5 => P = 2,5
2,2 2,2
Ti =
Pu
6 ⋅10 −3
=
= 0,005 => I = 1/Ti = 200
1,2
1,2
50
Control y Simulación del Modelo
_________________________________________________________________________
Gráfica 2: Respuesta del Caudal de GN ante variaciones del SP..
Como vemos en la figura hemos conseguido que el sistema se estabilice, pero
observamos demasiado amortiguación en la respuesta. Para optimizar el resultado
hemos aumentado el valor de Ti.
P=2
Ti = 0,02 => I = 1/Ti = 50
51
Control y Simulación del Modelo
_________________________________________________________________________
Gráfica 3: Respuesta del Caudal de GN ante variaciones del SP..
52
Control y Simulación del Modelo
_________________________________________________________________________
6.2.2 Ajuste del Resto de Controladores
Una vez visto como se ajustan los parámetros de un controlador, a continuación, se
muestra una tabla con los parámetros de los controladores de cada uno de los lazos de
control de la caldera.
LAZO DE CONTROL
PROPORCIONAL INTEGRAL
Control GN
2
50
Control AIRE
23
5000
Control RATIO
1
10
Control NIVEL
15
7
Control ATEMPERADOR
5
2
Control CALDERA
10
20
Tabla 14: Parámetros de los controladores.
A modo de comentario, ha habido controles que han tenido una dificultad añadida a la
hora de ajustar los parámetros. El control del RATIO tiene una dinámica muy lenta,
pues desde que actúa sobre el lazo de AIRE, hasta que analiza el oxígeno en los humos
de escape, pasa un tiempo y esto dificulta su estudio y su posterior ajuste.
53
Control y Simulación del Modelo
_________________________________________________________________________
6.3
Simulación de la Caldera
A continuación se describirán cada uno de los bloques simulados en el programa
Matlab, dando una explicación de su funcionalidad así como de su interrelación con el
resto de los bloques.
El conjunto de bloques se muestra de forma jerárquica a continuación:
§
§
§
CALDERÍN
o
BALANCE DE MATERIA
o
BALANCE DE ENERGÍA
o
CONTROL DE NIVEL
COMBUSTION
o
BALANCE DE MATERIA
o
BALANCE DE ENERGÍA ENTRADA
o
BALANCE DE ENERGÍA SALIDA
o
CALCULO DE O2 Y N2 NECESARIO
o
T. GASES
o
CALCULO DE LA CONCENTRACIÓN DE O2 EN HUMOS
RECALENTADOR
o
o
o
§
RECALENTADOR PRIMARIO
§
BALANCE ENERGÍA
§
TEMPERATURA SALIDA
§
T. GASES
RECALENTADOR SECUNDARIO
§
BALANCE ENERGÍA
§
TEMPERATURA SALIDA
§
T. GASES
CONTROL ATEMPERADOR
PRECALENTADOR DE AIRE
o
BALANCE ENERGÍA
o
TEMPERATURA SALIDA
o
T. GASES
§
CONTROL GAS
§
CONTROL AIRE
§
CONTROL RATIO
§
CONTROL CALDERA
§
COLECTOR VAPOR
54
Control y Simulación del Modelo
_________________________________________________________________________
6.3.1 Calderín
El bloque ‘calderín’ está formado por tres subbloques llamados ‘balance de materia’,
‘control de nivel’ y ‘balance de energía’.
El bloque ‘balance de materia’ calcula el nivel que tiene el calderín en cada momento
en función del agua de alimentación BFWH que entra al calderín y del vapor saturado
SH que sale. En este bloque también se calcula la temperatura del vapor saturado en
función de la presión P del propio calderín.
Una vez sabemos el nivel que tenemos, se intenta controlar a través del bloque ‘control
nivel’, el cual está compuesto de un controlador PI.
El bloque ‘balance de energía’ calcula en todo momento la presión del calderín a través
del calor que le llega, el agua de alimentación BFWH que entra, el vapor saturado SH
que sale y la presión P en el instante anterior.
Figura 12: Balance y control del calderín.
55
Control y Simulación del Modelo
_________________________________________________________________________
6.3.1.1 Balance de Materia
En este bloque se calcula el volumen a partir de los caudales en T/h de agua de
alimentación BFWH y de vapor saturado SH.
A través de la integración de la diferencia entre ellos obtenemos la masa en T
(toneladas) del agua que reside en el calderín. Para encontrar el volumen debemos
encontrar las densidades específicas del líquido y del vapor a través de la presión del
calderín en cada momento. Una vez encontradas multiplicamos por la masa y
encontramos el volumen.
Para hallar el nivel real del calderín suponemos que a 0 % de nivel la caldera tiene 20
m3 de volumen, y a 100 % la caldera tiene 40 m3. Por tanto, el limitador de volumen va
de 20 m3 a 40 m3, y el limitador de nivel va de 0 a 100 %.
Figura 13: Nivel del calderín.
56
Control y Simulación del Modelo
_________________________________________________________________________
6.3.1.2 Control de Nivel
El nivel es la variable a controlar a través de un controlador PI adecuadamente ajustado
para mantener el nivel del calderín en el punto de consigna deseado.
El controlador tiene como salida un valor OP que actúa sobre la válvula de
alimentación
de agua BFWH dándonos un caudal (variable manipulada).
La dinámica de la válvula se ha diseñado a través de un retardo de 1er orden con un
valor de la constante de T=1s.
G( s) =
1
Ts + 1
(47)
En el numerador de la función de transferencia se encuentra lo que llamaremos
característica de caudal de la válvula, que no es más que la expresión matemática o la
curva gráfica que proporciona el coeficiente de caudal de una válvula a lo largo de todo
el recorrido o carrera de su vástago (posición). En este caso, el valor de 0,7 viene de la
expresión:
Kc =
q max 70T / h
=
= 0,7
100%
Ymax
(48)
Es decir, que a 100 % de válvula hay un paso de caudal de 70 T/h.
Para facilitar los cálculos hemos optado por una válvula lineal, o sea que el coeficiente
de caudal, para cualquier apertura de la válvula, es proporcional a la carrera de la
misma a lo largo de todo su recorrido.
Figura 14: Control de nivel del calderín.
57
Control y Simulación del Modelo
_________________________________________________________________________
6.3.1.3 Balance de Energía
El balance energético del calderín consiste en aplicar la fórmula siguiente, que por otro
lado, ya se había analizado en el apartado 4.1, donde se estudiaba el modelado del
calderín.
K1 ⋅
dp
= Q − BFWH (hw − h f ) − SH ⋅ hc
dt
hc = hs − hw
(49)
(50)
Las entalpías del agua y del vapor las podríamos haber considerado fijas, ya que al
trabajar siempre alrededor de los 40 kg/cm2 de presión en el calderín, las variaciones
de entalpía son mínimas. No ha sido así, y para conseguir un modelo del calderín más
exacto se ha calculado las entalpías en cada momento y susceptibles de cambios en la
presión. Para hallar dichos valores, hemos introducido en una hoja de cálculo entalpías
y presiones, y a través de opciones de gráficas hemos conseguido las siguientes
ecuaciones:
Entalpía del vapor:
 kJ 
hs = 2619.6+15.941*P - 0.2806*P2  
 kg 
(51)
Entalpía del agua:
 kJ 
hw = 276.9+48.9493*P - 0.7054*P2  
 kg 
(52)
Al multiplicar estas entalpías por sus caudales correspondientes de agua BFWH o de
vapor SH, encontramos los caudales de calor que enfrían el calderín. Luego se le resta
del calor Q, que transportan los humos, y se integra el total, encontrando así la presión
del calderín.
58
Control y Simulación del Modelo
_________________________________________________________________________
Figura 15: Presión del calderín.
59
Control y Simulación del Modelo
_________________________________________________________________________
6.3.2 Combustión
En este bloque, por un lado se calcula el caudal de humos (T/h) que produce la
combustión a partir del GN y el AIRE, y por otro lado, la transferencia de calor QTOTAL
(MJ/h) que produce dicha reacción. Para ello se ha realizado un balance de materia
entre la entrada (combustible y comburente) y la salida (gases de escape o humos).
El circuito de los humos, que empieza en la combustión y llega hasta la chimenea, no
es más que un laberinto en el que los humos van cediendo calor a medida que van
avanzando. Por esta razón, para una mayor compresión se ha puesto nombre a los
humos, dependiendo del lugar del laberinto donde ceden el calor.
QTOTAL: Es la transferencia de calor que emite la combustión.
QRAD: Es la transferencia de calor que se cede a los tubos de la Zona de Radiación
(risers o tubos de subida al calderín).
QREC: Es la transferencia de calor que se cede a los tubos del Recalentador.
QCONV: Es la transferencia de calor que se cede a los tubos de la Zona de Conveccion
(down-comers o bajantes del calderín).
QPREC: Es la transferencia de calor que se cede a los tubos del Precalentador de Aire.
Q1 = QRAD + QCONV: Es la transferencia de calor que se cede al calderín.
Q2 = QREC + QPREC
QTOTAL = QRAD + QREC + QCONV + QPREC = Q1 + Q2
(53)
A continuación se presenta un esquema para entender mejor el calor que se va
cediendo en las diferentes partes de la caldera.
60
Control y Simulación del Modelo
_________________________________________________________________________
SH (VAPOR SATURADO)
CALDERÍN
BFWH
R
E
C
A
L
E
N
T
A
D
O
R
GN
QRAD
Q TOTAL
R
I
S
E
R
S
QREC
AIRE
QCONV
D
O
W
N
C
O
M
E
R
QPREC
P
R
E
C
A
L
E
N
T
A
D
O
R
AIRE
SH (VAPOR RECALENTADO)
Figura 16: Intercambios de calor en la caldera.
En este bloque también se calcula el tanto por ciento de O2 que se encuentra en todo
momento en los humos de salida, pues posteriormente se utilizará dicha variable para el
control del aire.
61
Control y Simulación del Modelo
_________________________________________________________________________
Figura 17: Transmisión de calor de la combustión.
62
Control y Simulación del Modelo
_________________________________________________________________________
6.3.2.1 Balance de Materia
Se calcula de forma estequiométrica la salida de todos los gases (GN, O2, N2, CO2, CO
y H2O), sabiendo que el 99% de Gas Natural es CH4 (Metano).
CH4 + 2O2 == CO2 + 2H2O
CH4 + 3/2O2 == CO + 2H2O
Para saber que proporción de los diferentes gases hay a la salida en función de la
reacción a la entrada, las unidades expresadas en toneladas por hora T/h se han pasado
a moles por hora mol/h. Así sabemos, por ejemplo, que para conseguir 2mol/h de H2O
se necesita 1 mol/h de CH4.
Se han tenido en cuenta varias premisas, ya descritas anteriormente en el apartado del
modelado, entre las cuales se encuentra que sólo el 95 % de CH4 reaccionará con el
aire, el otro 5% no reaccionará y se tratará como parte del humo de salida, y que del 95
% del CH4 quemado, sólo el 80% reaccionará para formar CO2 (dióxido de carbono), el
resto reaccionará para formar CO (monóxido de carbono).
Figura 18: Balance estequiométrico de los componentes de salida de humos a partir de los de entrada.
63
Control y Simulación del Modelo
_________________________________________________________________________
6.3.2.2 Balance de Energía Entrada
Calculamos las entalpías de los componentes de entrada de la combustión a partir de
las temperaturas de entrada, y en función de las capacidades caloríficas calculadas
previamente.
La temperatura del aire irá variando en función de la cantidad de aire que pasa por el
precalentador de aire y en función de la cantidad calor que contengan los humos que
pasen por dicho precalentador.
La temperatura de referencia la hemos considerado fija a 25 ºC.
La capacidad calorífica Cp del oxígeno van variando en función de la temperatura del
aire y se han calculado a partir de las siguientes ecuaciones:
 kg 
Cp O2 = (29.1 + 1.158*10-2*T - 0.6076*10-5*T2 +1.311*10-9*T3)/32 
 kJ ⋅º C 
 kg 
Cp N2 = (29 + 0.2199*10-2*T + 0.5723*10-5*T2 - 2.871*10-9*T3)/28 
 kJ ⋅º C 
La entalpía del GN es directa porque ya se ha encontrado calculada. Las entalpías del
O2 y del N2 se han encontrado aplicando la siguiente fórmula:
 kJ 
H = Cp ⋅ (T2 − T1 )  
 kg 
(54)
Posteriormente las entalpías calculadas son utilizadas para calcular el calor que hay a la
entrada, previo a la combustión.
Figura 19: Entalpías de los componentes de entrada.
64
Control y Simulación del Modelo
_________________________________________________________________________
6.3.2.3 Balance de Energía Salida
Calculamos las entalpías de los gases de salida de la combustión a partir de las
temperaturas de entrada, y en función de las capacidades caloríficas calculadas
previamente.
La temperatura de los humos es variable en función de la cantidad de GN que se esté
introduciendo a la combustión.
La temperatura de referencia es fija y de valor 25ºC.
Como en el apartado anterior, la búsqueda de la entalpía de cada componente se hace a
través de la siguiente fórmula:
 kJ 
H = Cp ⋅ (T2 − T1 )  
 kg 
(54)
De ahí que tengamos que encontrar previamente la capacidad calorífica de cada gas.
 kg 
Cp CH4 = (34.31 + 5.469*10-2*T + 0.3661*10-5*T2 – 11*10-9*T3)/16 
 kJ ⋅º C 
 kg 
Cp O2 = (29.1 + 1.158*10-2*T - 0.6076*10-5*T2 +1.311*10-9*T3)/32 
 kJ ⋅º C 
 kg 
Cp N2 = (29 + 0.2199*10-2*T + 0.5723*10-5*T2 - 2.871*10-9*T3)/28 
 kJ ⋅º C 
 kg 
Cp CO2 = (36.11 + 4.233*10-2*T - 2.887*10-5*T2 + 7.464*10-9*T3)/44 
 kJ ⋅º C 
 kg 
Cp CO = (28.95 + 0.411*10-2*T + 0.3548*10-5*T2 - 2.22*10-9*T3)/28 
 kJ ⋅º C 
 kg 
Cp H2O = (33.46 + 0.688*10-2*T + 0.7604*10-5*T2 - 3.593*10-9*T3)/18 
 kJ ⋅º C 
65
Control y Simulación del Modelo
_________________________________________________________________________
Figura 20: Entalpías de los componentes de salida.
6.3.2.4 Cálculo de O2 y N2 Necesario
En este bloque se calcula el O2 y N2 para la combustión a partir del aire de que
proviene del precalentador de aire, sabiendo que el aire se compone prácticamente por
el 79% de N2 y el 21% de O2.
Figura 21: Obtención del O2 y N2 a partir del aire.
66
Control y Simulación del Modelo
_________________________________________________________________________
6.3.2.5 Temperatura de Gases
La temperatura de los gases, que circulan por el exterior de los tubos de la caldera y
van circulando por el interior de la caldera desde el hogar hasta la salida del
precalentador de aire, van sufriendo cambios de temperatura en función de varios
factores de los cuales el más importante es la cantidad de combustible, en este caso el
GN, que se va quemando en la combustión. Por esta razón, se ha diseñado este bloque
para simular la dinámica que tendría la temperatura de los gases o humos en función de
la cantidad de GN que entrara a la caldera.
Respuesta Temporal
120
% Humos
100
80
60
40
20
0
0
5
10
15
Caudal GN (T/h)
Gráfica 4: Temperatura de los gases de escape a partir del caudal de GN.
A continuación, pasamos el % de humos a temperatura, sabiendo que el 100 % de
humos en la Zona de Radiación representa una temperatura de 1000 ºC.
Figura 22: Temperatura de los gases de escape a partir del caudal de GN.
67
Control y Simulación del Modelo
_________________________________________________________________________
6.3.3 Recalentador
En este bloque calculamos la temperatura de salida del vapor recalentado a partir de la
temperatura de entrada, el vapor saturado que sale del calderín y de la cantidad de
humos que calientan esta parte de la caldera.
Este recalentador está formado por dos subrecalentadores llamados primario y
secundario, entre los cuales se les inyecta un pequeño caudal de agua BFWH para
controlar la temperatura de salida del recalentador secundario.
El calor absorbido por los dos recalentadores Q3 + Q4, no es más que el calor cedido
por los humos en todo el conjunto del recalentador y que llamábamos QREC, y que
sumado con el calor cedido en el Precalentador de Aire QPREC, nos da el calor Q2.
En el esquema de la simulación se observa como el vapor SH de entrada al
recalentador no es el mismo que el de salida, ya que se le tiene que sumar la cantidad
de agua BFWH que se inyecta al vapor para controlar la temperatura de salida.
Figura 23: Sistema del recalentador.
68
Control y Simulación del Modelo
_________________________________________________________________________
6.3.3.1 Recalentador Primario
A partir de la temperatura de entrada y salida de los humos, que pasan por este
recalentador primario, calculamos las entalpías de cada uno de los componentes de los
humos a través de un Balance de Energía.
La temperatura de entrada de humos al recalentador primario es igual que la del
secundario, ya que físicamente los tubos se encuentran en paralelo. El incremento de
temperatura entre la salida y la entrada en el lado humos se ha considerado fija, de
valor 75 ºC.
El cálculo de las entalpías de cada uno de los componentes se ha hecho igual que en
apartados anteriores, aplicando la fórmula:
 kJ 
H = Cp ⋅ (T2 − T1 )  
 kg 
(54)
Las capacidades caloríficas se han calculado igual, con los mismos parámetros, que en
otros bloques de la simulación, con la diferencia que ahora las temperaturas son
diferentes.
Sabiendo el caudal de cada gas que compone los humos encontramos el calor Q3 que
ceden los gases en el recalentador primario y que coincide con el que absorbe el vapor
saturado.
La temperatura de salida del vapor TSH OUT se calcula en el bloque ‘Temperatura de
salida’, a partir del calor Q3, del vapor saturado que entra SH y de su temperatura TSH
IN, que en régimen estacionario será aproximadamente de 250 ºC.
Figura 24: Recalentador primario.
69
Control y Simulación del Modelo
_________________________________________________________________________
6.3.3.2 Recalentador Secundario
El recalentador secundario tiene la misma funcionalidad y actúa de la misma manera
que el recalentador primario. La única diferencia respecto el anterior es que la cantidad
de vapor de salida será diferente a la entrada del recalentador primario, ya que como
hemos dicho anteriormente tenemos un atemperador entre ambos recalentadores, el
cual inyecta una pequeña cantidad de agua BFWH que hará variar la cantidad de vapor
a la salida.
Figura 25: Recalentador secundario.
70
Control y Simulación del Modelo
_________________________________________________________________________
6.3.3.3 Control Atemperador
Controla la temperatura de salida del vapor recalentado, con una consigna aproximada
de 395 ºC, inyectando agua a la entrada del recalentador secundario. La cantidad
máxima de agua que puede inyectar es de 5 T/h variando la temperatura hasta 30 ºC.
El controlador PI da una señal a la válvula dejando pasar más o menos agua. Esta
válvula se ha modelado con un retardo de primer orden con un valor de la constante de
T=1s.
G( s) =
1
Ts + 1
(55)
El valor de la característica de caudal de la válvula, que por cierto es lineal, viene dada
por la siguiente expresión:
Kc =
q max 5T / h
=
= 0,05
Ymax 100%
(56)
Es decir, que a 100% de válvula hay un paso de caudal de 5T/h.
Luego, hay que saber que temperatura real tenemos en la entrada del recalentador
secundario TSH IN2, una vez hayamos inyectado cierta cantidad de agua BFWH. Para
ello, transformamos el caudal en temperatura a través también de un retardo de primer
orden de constante T=1, y una relación lineal y proporcional entre el caudal que
introducimos y la temperatura:
Kc =
Tmax 150º C
=
= 30
5T / h
q max
(57)
La temperatura resultante se suma a la que sale del recalentador primario TSH OUT1,
y obtenemos la que entra al recalentador secundario TSH IN2.
Figura 26: Atemperador.
71
Control y Simulación del Modelo
_________________________________________________________________________
6.3.4 Precalentador de Aire
Una vez calculamos a través de un balance de energía la cantidad de calor que
desprenden los humos en el precalentador, medimos la temperatura de salida del aire
del precalentador hacia la combustión, a través de la cantidad de aire que necesita dicha
combustión en cada momento.
El modelo es muy parecido al del recalentador primario y secundario, la diferencia se
encuentra en el decremento de temperatura que sufre, que es de 100 ºC.
Figura 27: Sistema de calentamiento de aire de entrada.
72
Control y Simulación del Modelo
_________________________________________________________________________
6.3.5 Control del GN
Controlamos la apertura de la válvula de gas natural y en consecuencia el paso de
caudal hacia la combustión.
Dicho control se puede realizar de dos maneras en Automático o en Cascada.
En Automático, nosotros le damos un valor de consigna de caudal en T/h y el
controlador PI regula la salida de la válvula para que la variable manipulada y
controlada, en este caso el caudal de entrada de GN a la caldera, se ajuste al valor
pedido.
En Cascada, el control de la válvula en sí funciona igual, la única diferencia radica en
que el punto de consigna, ahora ya no es dado por nosotros sino que viene dado por la
salida de otro control, en este caso por el control de la caldera.
La válvula de Gas Natural se ha diseñado con un retardo de primer orden con un valor
de la constante de T=1s.
G( s) =
1
Ts + 1
(58)
La característica de caudal de la válvula lineal, viene dada por la siguiente expresión:
Kc =
q max 12T / h
=
= 0,12
Ymax 100%
(59)
Es decir, que a 100% de válvula hay un paso de caudal de gas de 12 T/h.
Figura 28: Control del caudal de GN.
73
Control y Simulación del Modelo
_________________________________________________________________________
6.3.6 Control del Aire
Al igual que en el caso anterior, este bloque controla la apertura de la válvula de
entrada de aire a la caldera para el proceso de combustión con el GN.
También tiene la posibilidad de tener un control en Automático en función del valor de
consigna dado por nosotros o en Cascada en función de la salida del control de la
caldera.
A diferencia del caso anterior, el valor real de aire que tenemos después de la válvula
de aire, antes de ajustarse con el punto de consigna en el controlador PI, debe
multiplicarse por una variable llamada RATIO (GN/AIRE) para reducir inquemados en
la combustión y ajustar el tanto por ciento de oxígeno en la salida de los humos.
Esta variable controlada (RATIO) también puede ser asignada por nosotros, de forma
que el control trabajaría en Automático, o por el propio control del Ratio, de forma que
trabajaría en Cascada.
La válvula de aporte de aire a la caldera, para una posterior combustión con el GN,
tiene un cierto retardo desde que se le da la orden de abrir o de cerrar, hasta que
realmente realiza la acción. Es por esta razón, que dicha válvula se ha modelado con un
retardo de primer orden con un valor de la constante de T=1s.
G( s) =
1
Ts + 1
(60)
La válvula de aire se puede considerar lineal, ya que su paso de aire es proporcional a
la apertura, de forma que la característica de caudal de la válvula lineal, viene dada por
la siguiente expresión:
Kc =
q max 220T / h
=
= 2,2
Ymax
100%
(61)
Es decir, que a 100% de válvula hay un paso de caudal de aire de 220T/h.
Figura 29: Control de aire de entrada.
74
Control y Simulación del Modelo
_________________________________________________________________________
6.3.7 Control del Ratio
Como ya se ha comentado en el apartado anterior, este bloque toma el % de O2 en los
humos de salida y en función del análisis aumenta el RATIO, cosa que reduciría la
cantidad de Aire a la combustión, o disminuiría el RATIO cosa que aumentaría el Aire
a la combustión.
RATIO =
GN
AIRE
(62)
Desde que se realiza el análisis de % de oxígeno hasta que se toma la acción de
aumentar o disminuir el aire pasa un tiempo que es simulado con un retardo de primer
orden, con una constante de tiempo T=1s.
El RATIO es una variable que puede ir de 0,5 a 1, por tanto la característica de caudal
de la válvula lineal, viene dada por la siguiente expresión:
Kc =
∆ max (1 − 0,5)
=
= 0,005
Ymax
100%
(63)
Es decir, que el 0% corresponde a un factor de 0,5, y el 100% corresponde a un factor
de 1. Este valor se multiplicará por el valor real del aire que tengamos en ese momento,
de forma que variará la diferencia entre el SP del aire y la PV del aire. Si aumentamos
el RATIO aumentará la PV del aire, hecho que hará bajar la salida OP a la válvula del
aire y en consecuencia bajará la cantidad de aire a la caldera, y viceversa.
En la figura se observa como antes del controlador PI hay un selector auto/manual. Nos
interesa que cuando estemos controlando el Ratio en manual, el controlador no
empiece a calcular, porque sino fuera así, al pasar el lazo a automático el error podría
ser muy grande.
Figura 30: Control del Ratio.
75
Control y Simulación del Modelo
_________________________________________________________________________
6.3.8 Control de la Caldera
Este bloque tiene por un lado una salida de SP de GN y por otro lado una salida de SP
de Aire, que van a los diferentes bloques de control de GN y control de Aire.
Estas variables son valores necesarios para mantener la presión del colector a lo
estipulado por el punto de consigna de este bloque en kg/cm2. A este SP le llamaremos
MASTER del colector de vapor.
La forma de calcular las dos salidas de este bloque manda sobre la filosofía de evitar
siempre la aparición de inquemados en los humos de salida. Por esta razón ante una
bajada de presión del colector de vapor primero actuará la variable del aire aumentado
su aporte y luego aumentará la variable de GN. Ante una subida del colector de vapor
primero bajaremos el aporte de GN a la caldera y luego el aporte de Aire.
Figura 31: Control de GN y Aire en función de la presión del colector.
76
Control y Simulación del Modelo
_________________________________________________________________________
6.3.9 Control del Colector de Vapor
El colector de vapor se ha simulado como si fuera un gran depósito a una presión
determinada PCOL, donde hay un solo aporte dado por nuestra caldera SH, que variará
en función de la diferencia de presiones entre el colector y el calderín. Es decir, cuando
la presión del calderín supere la presión del colector entonces la caldera empezará a
producir vapor.
El colector de vapor tiene por tanto una entrada de SH que será lo producido por
nuestra caldera y una salida llamada SHCOL que será el consumo de otros clientes de
este colector de vapor, y que podrá ser variado por nosotros.
Por tanto, el consumo de los diferentes clientes de este colector será aproximadamente
la producción de vapor de la caldera. Ante una subida del consumo de los clientes,
aparecerá una bajada de presión en el colector y en consecuencia un aumento en la
producción de la caldera. El caso contrario, ante una disminución de la importación de
vapor por parte de los clientes, habrá un aumento de la presión del colector y por tanto
una disminución de la producción de la caldera.
Si nos fijamos en la figura, el colector de vapor se ha modelado de la siguiente forma:
PCOL = ∫
45
0
1
(SH − SHCOL)dt
C
(64)
donde el valor de C se ha buscado de forma empírica, teniendo en cuenta la dinámica
del colector comparándolo con casos reales.
 T

C = 25 
2
 kg / cm 
Para calcular el valor de SH que sale de la caldera se ha buscado la diferencia entre la
presión del calderín y la del colector, sabiendo que con una diferencia máxima de 0,5
pasa la máxima producción de la caldera, 70 T/h de vapor. Y además la relación es
lineal y proporcional para cualquier apertura de la válvula (válvula de clapeta).
Figura 32: Modelado del colector de vapor.
77
Control y Simulación del Modelo
_________________________________________________________________________
6.3.10 Esquema General de la Caldera
Figura 33: Modelado de la Caldera.
78
Resultados Obtenidos
_________________________________________________________________________
7
Resultados Obtenidos
Una vez explicados los controles y las partes que forman la caldera, pasamos a
visualizar el comportamiento y la dinámica que tiene la caldera a través de
perturbaciones, que en un caso real serían provocadas por un operador.
Para dicho propósito pasamos a analizar cada una de estas perturbaciones por separado,
para ver posteriormente como afectan a otras variables y controles del modelo.
7.1
Condiciones Iniciales
Para el análisis del modelo partimos de unas condiciones iniciales que ya se han ido
comentando a lo largo del proyecto. La caldera está en marcha con una presión en el
calderín de aproximadamente 40kg/cm2 de presión y 250ºC de temperatura. Para llegar
a esa presión la caldera previamente a tenido que estar en marcha con un cierto
consumo de combustible. Una vez pasado este tiempo, que lo podemos llamar
transitorio, la caldera se puede considerar estable, y es entonces cuando puede
realizarse el estudio, considerándose los valores significativos.
7.2
Consumos en el Colector de Vapor
Para ver como varían cada uno de los parámetros, realizaremos perturbaciones en el
consumo de vapor que realizarían, en un hipotético caso, los clientes del colector. En el
estudio partiremos de un consumo de 20 T/h, que pasará a ser de 30T/h, luego de
40T/h, nuevamente de 30T/h y finalmente de 20T/h, con espacios de tiempo entre
saltos de 50s. Pasado este tiempo, analizamos cada una de las variables de la caldera,
susceptibles a cambios importantes, como el nivel, la presión y la temperatura del
calderín, el caudal de aire a la caldera y su temperatura de entrada a la misma, etc.
79
Resultados Obtenidos
_________________________________________________________________________
7.2.1 Nivel del Calderín
Gráfica 5: Nivel del calderín.
Durante la simulación se ha mantenido el nivel del calderín al 50%, aunque como ya
sabemos existe la posibilidad de modificar el set point al valor que nosotros deseemos
en función de las circunstancias. El control de nivel es bastante estable, pero como ya
he dicho en alguna otra ocasión, al principio de la simulación y hasta que no han
transcurrido un cierto tiempo hasta que el sistema se estabiliza, el nivel oscila bastante.
Lógicamente para el estudio no tendremos en cuenta este tiempo de simulación.
Ante una subida del consumo de vapor por parte de los clientes y una baja de la presión
del colector, la producción de vapor de la caldera aumenta. En un primer momento,
como aumenta el consumo de vapor, el nivel del calderín disminuye hasta que el
controlador actúa y abre la válvula de agua de alimentación BFWH hacia el calderín.
En una bajada del consumo de vapor, pasa exactamente lo contrario, al principio como
disminuye el consumo de vapor, el nivel del calderín aumenta hasta que cierra la
válvula de agua. Luego la válvula ajusta su apertura hasta estabilizar el nivel al 50%.
80
Resultados Obtenidos
_________________________________________________________________________
7.2.2 Presión del Calderín
Gráfica 6: Presión del calderín.
La presión de diseño del calderín es de 40kg/cm2, pero si nosotros intentáramos
mantener esta presión, venteando vapor por algún punto de la caldera, y la presión del
colector estuviera por encima, como es el caso a 41kg/cm2, lógicamente nunca
descargaríamos al colector por una cuestión de diferencia de presiones. Por tanto, el
calderín de nuestra caldera trabajará bajo demanda, es decir, producirá si y sólo si la
presión de colector es inferior a la del calderín.
Si sube el consumo de vapor, disminuyendo la presión del colector, en el primer
instante la presión del calderín también disminuye, porque genera más vapor de lo que
estaba generando, es decir, tiene más facilidad para descargar. A posteriori, actúan las
válvulas de gas y aire abriendo, subiendo la presión del calderín y en consecuencia la
producción.
En el caso contrario, en el momento que baja el consumo de vapor y aumenta la
presión del colector, la presión del calderín también aumenta porque el vapor que
estaba generando lo deja de generar, es como si estranguláramos la válvula de salida.
Luego, actúan las válvulas de gas y aire cerrando, bajando así la presión del calderín y
en consecuencia la producción ya que la presión del colector se estabilizará en
41kg/cm2.
81
Resultados Obtenidos
_________________________________________________________________________
Una vez explicado el comportamiento de la señal, si nos fijamos en la figura,
observamos como lo explicado hasta ahora tiene el mismo comportamiento de señales
que tienen ‘el efecto de fase no mínima’. Esto es, cuando a un sistema le inyectamos,
por ejemplo, una señal escalón de amplitud +1 y en un primer momento la respuesta
tiene la intención de bajar, pero luego se estabiliza en +1. Lo mismo pasaría si a este
sistema le metemos una señal escalón de amplitud –1, en un primer momento intentaría
subir pero luego se estabilizaría en el valor de –1.
En el lenguaje de control, este efecto aparece cuando el sistema, representando el
L.G.R., tiene ceros en el semiplano derecho. Por ejemplo, la siguiente función de
transferencia simularía exactamente este comportamiento:
s −1
s + s + 10
2
82
Resultados Obtenidos
_________________________________________________________________________
7.2.3 Temperatura del Calderín
Gráfica 7: Temperatura del calderín.
La temperatura del vapor de saturación, que sale del calderín y que luego se dirige al
recalentador, tiene por diseño una temperatura de 250ºC a 40kg/cm2. Lógicamente en
la práctica este valor no es fijo, sino que varía en función de la cantidad de vapor que
sale del calderín, de la presión del mismo e incluso del nivel. En la figura observamos
como a medida que vamos subiendo la producción de la caldera, la temperatura va
subiendo. Aumenta porque la presión que sufre el calderín también sube. Es más, la
amortiguación de la respuesta es debido principalmente a la variación que sufre la
presión del calderín ante una bajada o subida de la producción de vapor.
83
Resultados Obtenidos
_________________________________________________________________________
7.2.4 Caudal de GN a la Caldera
Gráfica 8: Caudal de GN.
Es lógico pensar que ante una subida del consumo de vapor, la caldera debe ser capaz
de aumentar su producción a través de un mayor caudal de combustible. De esta
manera, producir más gases con más calorías, capaces de calentar los tubos de la
caldera, y por radiación y/o convección calentar el agua, produciendo más vapor. Lo
mismo para el caso contrario, para disminuir la cantidad de vapor que lanzamos al
colector se deberá disminuir la cantidad de combustible. Esto es lo que se refleja
claramente en la figura.
Como comentario, añadir que ante una subida de producción de la caldera primero
abrirá la válvula de aire y luego la del gas natural y ante una bajada de producción
primero cerrará la válvula de gas natural y luego la de aire para no producir
inquemados (humo negro en la chimenea).
84
Resultados Obtenidos
_________________________________________________________________________
7.2.5 Caudal de Aire a la Caldera
Gráfica 9: Caudal de aire.
La subida o la bajada del consumo de vapor se refleja también en el aumento o
disminución del caudal de aire necesario para una combustión correcta en la caldera.
Recordemos que este caudal variará en función de la presión del colector de vapor, que
a su vez está ligado al consumo de vapor por parte de los clientes.
Una bajada de la presión del colector, provocado por un aumento en el consumo del
vapor, primero abrirá la válvula del aire y luego la del GN, para no producir
inquemados. De la misma manera, ante una subida de la presión del colector,
provocado por una disminución del consumo del vapor, primero cerrará la válvula de
GN y luego cerrará la de aire, por la misma razón, para que siempre exista exceso de
oxígeno y no se produzcan inquemados.
La estabilización del caudal de aire, a la demanda establecida, será variable en el
tiempo dependiendo del parámetro RATIO, que recordemos, hace un análisis de O2 en
los humos de escape y en función de dicho análisis incrementa o decrementa la
posición de la válvula de aire aumentando o disminuyendo el caudal de aire a la
combustión.
85
Resultados Obtenidos
_________________________________________________________________________
7.2.6 Temperatura de Aire a la Caldera
Gráfica 10: Temperatura del aire.
La temperatura del aire de entrada a la caldera se caliente previamente en el
Precalentador de Aire, a través del calor de los humos que ceden al pasar por el exterior
de los tubos. Como se ve en la figura, la temperatura del aire aumentará en el momento
que exista un incremento de la producción de la caldera, y disminuirá en el caso
contrario. El aumento de la producción de vapor se basa en un aumento de combustible
hacia la caldera y en consecuencia un aporte mayor de calorías debido a un aumento de
los humos de escape.
Hay que destacar el incremento de temperatura que sufre el aire al aumentar la
producción de la caldera de 20T/h a 30T/h, y en cambio la pequeña variación de
temperatura que sufre cuando pasamos a producir 40T/h. La explicación se basa en que
al aumentar la producción también aumenta la cantidad de aire hacia la caldera para
que se produzca una correcta combustión. Al aumentar la cantidad de aire, aunque se
aumente el calor en el Precalentador de Aire, éste también aumenta su caudal y cuesta
más de calentar.
86
Resultados Obtenidos
_________________________________________________________________________
7.2.7 Presión del Colector de Vapor
Gráfica 11: Presión del colector de vapor.
La presión del colector de vapor la controlamos nosotros, en un caso hipotético el
operador, manteniéndola a 41kg/cm2. Podríamos haber mantenido la presión siempre
fija en un valor sin posibilidad de manipularla, pero en un complejo industrial donde de
un colector de vapor hay varios productores (calderas de vapor) y diferentes clientes
(turbinas, compresores,...), es importante poder jugar con esta variable, porque al bajar
el SP podemos ayudar a productores a sacar el vapor de sus calderas, en el caso que
tuvieran problemas por diferencia de presiones entre su colector y el nuestro.
Es lógico entender que en un complejo industrial sólo habría un solo operador que
controlara la presión de vapor, es decir sólo habría un MASTER de presión, el resto de
calderas irían gobernadas en función de dicho MASTER.
Referente a la figura que se presenta en este apartado, vemos como ante un consumo de
los clientes, aparece una bajada de la presión del colector que luego se estabiliza con la
producción de vapor de la caldera. Cuando tenemos una disminución del consumo, la
presión del colector aumenta y la caldera intenta disminuir su producción.
87
Resultados Obtenidos
_________________________________________________________________________
7.2.8 Temperatura del Vapor de Salida de la Caldera
Gráfica 12: Temperatura de vapor de salida.
La temperatura del vapor recalentado está controlada por un atemperador que inyecta
agua de alimentación a calderas BFWH a una presión superior a la del vapor
(PBFWH=70kg/cm2) entre el recalentador primario y el secundario. Esto obliga a
mantener siempre una temperatura estipulada por el operador alrededor de los 395ºC.
Por tanto, ante subidas o bajadas de la producción de vapor, la temperatura siempre
deberá ser de 395ºC. Lógicamente, y como se observa en la figura, hay un tiempo de
estabilización entre el momento que el consumo de vapor por parte de los clientes
aumento o disminuye, y se empieza a controlar la temperatura, entre otras cosas porque
también hay variaciones de producción de vapor.
En un primer momento, ante una subida del caudal de vapor, la temperatura tiene a
subir rápidamente por que al atemperador aún no le ha dado tiempo a inyectar agua, y
viceversa en el caso contrario.
88
Resultados Obtenidos
_________________________________________________________________________
7.2.9 Consumo del Colector de Vapor
Gráfica 13: Consumo del colector de vapor.
Ante un aumento del consumo por parte de los clientes del colector de vapor, la presión
del colector de vapor disminuye. En ese momento la caldera consume más combustible
para contrarrestar dicha bajada de presión, aumentando así la producción de vapor, tal
y como se observa en la figura en los dos primeros saltos.
Vemos como la respuesta tarda en estabilizarse aproximadamente unos 30 segundos,
cosa que por otro lado es normal, porque desde que el cliente aumenta el consumo de
vapor, hasta que la caldera empieza a producir hay un tiempo en el que la válvula de
aire abre, luego abre la válvula de gas, hay una combustión en el que se producen gases
que calientan los tubos de la caldera y una vez más calientes producen más vapor.
A partir de T=150s, los clientes empiezan a disminuir el consumo, hecho que hace
aumentar la presión del colector, y en consecuencia bajar la producción de la caldera.
Si nos fijamos en la figura, tanto al aumentar el consumo como al disminuirlo, aparece
un cierto off-set en la producción de la caldera, que es debido a la inyección de agua
BFWH que añadimos en el atemperador del recalentador. Este off-set se hace mayor
cuanto mayor es la producción de la caldera. Esto es debido a que cuanto mayor es la
exportación de vapor, mayor es la cantidad de gases que pasa por los tubos, siendo
89
Resultados Obtenidos
_________________________________________________________________________
mayor también la temperatura que calientan estos tubos. De forma que, auque el paso
de más caudal de vapor por el recalentador refrigere los tubos, la temperatura del vapor
es más alta, y por tanto, hay que añadir más agua cuanto mayor sea el caudal de vapor
que salga de la caldera.
90
Resultados Obtenidos
_________________________________________________________________________
7.3
Variaciones en el SP de O2
En este apartado observaremos como se comporta el control de aire y el control de ratio
ante variaciones en el set point de O2. Para ello estudiaremos el comportamiento de las
diferentes variables susceptibles a cambios, en un margen de tiempo de 250 segundos,
variando el SP de O2 entre 3% y 5%.
7.3.1 Caudal de Aire
Vemos como al aumentar la cantidad de O2 en los humos de salida, lógicamente el aire
necesario en la combustión también aumenta, ya que necesitamos un exceso de aire. El
caso contrario también se refleja en la gráfica, pues ante una bajada del SP de o2 la
cantidad de aire disminuye.
Caudal de Aire
75
Caudal
70
65
60
0
50
100
150
200
250
Tiempo
Gráfica 14: Caudal de aire.
Para conseguir este propósito hay que entender como funciona el control del Ratio
(GN/AIRE). Primero comparamos el set point de O2 con el que tenemos a la salida de
los humos. El controlador nos da una salida que multiplicada por una constante nos da
el Ratio. Este valor lo multiplicamos por la cantidad de aire que entra a la caldera,
siendo el resultado, el valor que se compara con el set point de aire en el control de
91
Resultados Obtenidos
_________________________________________________________________________
aire. De forma que, cuando queremos aumentar el % de O2 en humos, el Ratio
disminuirá. Al disminuir, el producto de éste con el aire, que entra en la caldera en ese
momento, disminuirá también, de forma que la diferencia entre el set point del aire y
dicho valor será mayor, y la válvula de aire querrá corregir, aumentando su valor y en
consecuencia dejando pasar más aire hacia la caldera.
Respuesta del RATIO en funcion del O2
% de O2 en Humos
1
6
5.5
0.95
5
4.5
Ratio
Ratio
0.9
0.85
4
3.5
3
0.8
2.5
2
0.75
0
50
100
150
200
0
250
50
100
150
200
250
Tiempo
Tiempo
Gráfica15: Ratio y O2 en humos.
La temperatura de aire disminuye su valor ante una subida de caudal, ya que cuanto
más caudal pasa más refrigerada está la tubería. Y ante una bajada de caudal de aire,
sufre un aumento relativo de la temperatura por el mismo motivo.
92
Resultados Obtenidos
_________________________________________________________________________
Temperatura del Aire
158
157
156
Temperatura
155
154
153
152
151
150
0
50
100
150
Tiempo
Gráfica 16: Temperatura del aire.
93
200
250
Resultados Obtenidos
_________________________________________________________________________
7.3.2 Caudal de GN
Un aumento de aire en la combustión se convierte en una pequeña disminución del
combustible, y viceversa. Esto es debido a que si no hay variaciones en la producción
de la caldera, la cantidad de calorías necesarias no varían, pero si variamos una de las
fuentes que producen estas calorías como es el caso del aire, la otra fuente, que es el
GN, contrarresta la situación disminuyendo o aumentando su valor.
Caudal de GN
8
7
Caudal
6
5
4
3
2
0
50
100
150
Tiempo
Gráfica 17:Caudal de GN
94
200
250
Resultados Obtenidos
_________________________________________________________________________
7.4
Conclusiones
Una vez vistos los resultados, podemos decir que el diseño de nuestro simulador
responde bien a los objetivos que se plantearon al principio del proyecto, y constituye
una herramienta muy buena para profesionales de la industria y estudiantes, aplicable a
cualquier caldera de vapor de cualquier complejo o planta química.
El simulador tiene las siguientes características:
•
Constituye un sistema modular claro y de fácil manejo. El diseño a través de
bloques permite diferenciar cada una de las partes de la caldera.
•
Permite el acceso rápido a cualquier constante, variable, o ecuación matemática
susceptible de ser modificada a petición del usuario.
•
Podemos simular procesos reales modificando las variables del proceso normal,
llevándolas a condiciones extremas, difíciles de conseguir en la realidad, viendo así
el comportamiento de la caldera.
•
Cabe la posibilidad de hacer gráficas de cualquier variable del sistema, con el
objetivo de observar el proceso en un intervalo de tiempo determinado, y con una
respuesta en régimen estacionario fiable.
7.5
Agradecimientos
A Sr. Francisco Javier Calvente Calvo por su ayuda prestada y su estrecha colaboración
durante el desarrollo del proyecto.
95
Anexo
_________________________________________________________________________
8
Anexo
8.1
Instrucciones de Matlab para la generación de las gráficas
%ARCHIVO CALDERA.m UTILIZADO PARA LA VISUALIZACION DE LAS GRAFICAS.
%CALDERIN
%NIVEL DEL CALDERIN
figure(1)
plot(NIVEL.time,NIVEL.signals.values)
axis([0 250 48 52])
title(['Nivel del Calderin'])
xlabel('Tiempo')
ylabel('Nivel')
%PRESION DEL CALDERIN
figure(2)
plot(PRESION.time,PRESION.signals.values)
axis([0 250 40.5 42])
title(['Presion del Calderin'])
xlabel('Tiempo')
ylabel('Presion')
%TEMPERATURA DEL VAPOR SATURADO
figure(3)
plot(TEMPERATURA.time,TEMPERATURA.signals.values)
axis([0 250 251 253])
title(['Temperatura del Calderin'])
xlabel('Tiempo')
ylabel('Temperatura')
%COMBUSTION
%CAUDAL DE AIRE A LA CALDERA
figure(4)
plot(AIRE.time,AIRE.signals.values)
axis([0 250 60 75])
title(['Caudal de Aire'])
xlabel('Tiempo')
ylabel('Caudal')
%TEMPERATURA DEL AIRE HACIA LA CALDERA
96
Anexo
_________________________________________________________________________
figure(5)
plot(T_AIRE.time,T_AIRE.signals.values)
axis([0 250 150 158])
title(['Temperatura del Aire'])
xlabel('Tiempo')
ylabel('Temperatura')
%CAUDAL DE GAS NATURAL A LA CALDERA
figure(6)
plot(GN.time,GN.signals.values)
axis([0 250 2 8])
title(['Caudal de GN'])
xlabel('Tiempo')
ylabel('Caudal')
%TANTO POR CIENTO DE OXIGENO EN HUMOS
figure(7)
plot(O2.time,O2.signals.values)
axis([0 250 2 6])
title(['% de O2 en Humos'])
xlabel('Tiempo')
ylabel('Ratio')
%RATIO
figure(8)
plot(RATIO.time,RATIO.signals.values)
axis([0 250 0.75 1])
title(['Respuesta del RATIO en funcion del O2'])
xlabel('Tiempo')
ylabel('Ratio')
%VAPOR DE SALIDA DE LA CALDERA
%TEMPERATURA DEL VAPOR RECALENTADO
figure(9)
plot(T_VAPOR.time,T_VAPOR.signals.values)
axis([0 250 375 410])
title(['Temperatura del Vapor de salida del Recalentador'])
xlabel('Tiempo')
ylabel('Temperatura')
%CONSUMO DEL COLECTOR DE VAPOR
97
Anexo
_________________________________________________________________________
figure(10)
plot(COLECTOR.time,COLECTOR.signals.values)
axis([0 250 10 55])
title(['Consumo del colector de Vapor'])
xlabel('Tiempo')
ylabel('Caudal')
%PRESION DEL COLECTOR DE VAPOR
figure(11)
plot(P_COLECTOR.time,P_COLECTOR.signals.values)
axis([0 250 40.4 41.6])
title(['Presion del colector de Vapor'])
xlabel('Tiempo')
ylabel('Presion')
98
Referencias y Bibliografía
_________________________________________________________________________
9
Referencias y Bibliografía
[1]
PRINCIPIOS ELEMENTALES DE LOS PROCESOS QUÍMICOS
Editorial: Addison-Wesley Iberoamericana
Autor: Richard M.Felder y Ronald W.Rousseau
[2]
FUNDAMENTOS DE TERMODINÁMICA TÉCNICA
Editorial: Reverté. S.A.
Autor: M.J.Moran y H.N.Shapiro
[3]
TERMODINÁMICA TÉCNICA
Editorial: Reverté. S.A.
Autor: José Segura
[4]
TERMODINÁMICA APLICADA
Editorial: Edicions Universitat de Barcelona
Autor: Rosa Albalat
[5]
CONTROL DE PROCESOS
Editorial: Edicions UPC.
Autor: Alfred Roca Cusidó
[6]
CONTROL AVANZADO DE PROCESOS. Teoría y Práctica
Editorial: ISE
Autor: J. Acedo Sánchez
[7]
PERRY’S CHEMICAL ENGINEERS’ HANDBOOK
Editorial: Mc Graw Hill
[8]
DRUM-BOILER DYNAMICS
Artículo sobre el estudio de la dinámica de una caldera convencional, encontrado en la página web
Autor: K.J.Aström, R.D. Bell
www.elsevier.com/locate/automatica
99