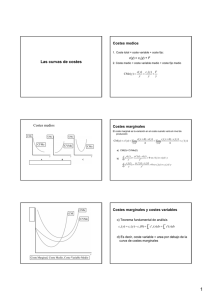
Competencia perfecta
Anuncio

UNIVERSIDAD DE LA REPÚBLICA FACULTAD DE CIENCIAS ECONÓMICAS Y ADMINISTRACIÓN MICROECONOMÍA AVANZADA SOLUCIÓN EJERCICIOS DE COMPETENCIA PERFECTA 1. AVENA a. Función de demanda isoelástica: y = Ap − B , B > 0 ε = A(− B ) p − B −1 p = −B Ap − B Si y d = 6.000 = A(10) Si y O = 5.000 = −1 → A = 60.000 → y D = 60.000 P 60.000 → P = 12 P b. Campaña publicitaria: y d = 6.600 = A(10) −1 → A = 66.000 → y D = 66.000 = 5.000 → P = 13.2 P 2. 1000 EMPRESAS IDÉNTICAS a. O( P ) = 100.000 = D( P ) = 160.000 − 10.000 P → P = 6 b. Nuevo precio de equilibrio si: i. Si la oferta de la empresa es cero → O ( P ) = 99.900 = D( P ) = 160.000 − 10.000 P → P = 6.01 ii. Si la oferta de la empresa es 200 → O( P ) = 100.100 = D ( P ) = 160.000 − 10.000 P → P = 5.99 6 = −0.6 c. Elasticidad del mercado: ε = −10.000 100.000 6 Elasticidad de la empresa: ε i = −10.000 = −600 100. La empresa se enfrenta a una demanda más elástica, un cambio en la cantidad ofrecida no afecta mucho el precio 3. 100 EMPRESAS IDÉNTICAS 1 2 Q Q + 0.4Q + 4 = ( + 2) 2 = P → Q = 10 P − 20 100 10 b. Q = 1.000 P − 2.000 a. CMa(Q) = c. P=25; Q=3000 1 4. MAIZ a. P = 5 = CM = b. CM = P → c. Q + 1 → Q = 40kilos 10 Q + 1 = P → Q = 10 P − 10 10 IT = P[Q + R (Q )] ⎡Q 2 ⎤ ⎤ 40 − Q ⎤ ⎡ Q 2 P Q2 ⎡ + Q ⎥ = P ⎢Q + − + Q = Q ( − 1 ) − + 20 P ⎢ ⎥ 2 ⎥⎦ ⎣ 20 2 20 ⎣ ⎣ 20 ⎦ ⎦ π (Q) = P[Q + R(Q)] − ⎢ d. Si P=5 ∂π (Q) P Q Q = ( − 1) − = 0 → ( P − 2) = → Q = 5 P − 10 ∂Q 2 10 5 Q = 5P − 10 → Q = 5 * 5 − 10 = 15 y las reservas serán R (Q) = 40 − 15 = 12.5 2 e. Cuantía en $ dela subvención: R (Q) = f. 40 − Q 40 − (5 P − 10) 5 y Q = 5 P − 10 → R( P ) = = 25 − P 2 2 2 La oferta al mercado será su producción más las R que recibe como subvención: O(Q ) = Q + 40 − Q Q 5 P − 10 5 = + 20 pero Q = 5 P − 10 → O( P ) = + 20 = P + 15 2 2 2 2 si P=5 entonces la oferta será 27.5 kilos 5. GASOLINA a. Largo Plazo: CME=P y CM=P CME=CM b. 0.01Q − 1 + 100 100 10.000 = 0.02Q − 1 → = 0.01Q → = Q → Q 2 = 10.000 → Q = 100 Q Q Q CME = CM = P = 1 2 Qd = 2.500.000 − 500.000 * 1 = 2.000.000 c. → estaciones = 2.000.000 = 20.000 100 d. Si cambia la demanda Qd = 2.000.000 − 1000.000 * 1 = 1.000.000 → estaciones = 1.000.000 = 10.000 100 6. En un mercado perfectamente competitivo coexisten dos tipos de empresas. Las del tipo 1 tienen costes totales representados analíticamente por la función 4 ± 16 − 4 x6(6 − P) 2 x6 8 ± 64 − 4 x6(2 − P) C 2 (q ) = 2q 3 − 4q 2 + 2q → CMa 2 (q ) = 6q 2 − 8q + 2 = P → q 2 = 2 x6 C1 (q ) = 2q 3 − 2q 2 + 6q → CMa1 (q ) = 6q 2 − 4q + 6 = P → q1 = El signo de menos que precede la raíz cuadrada no debe tenerse en cuenta porque corresponde la situación en la que no se cumple la condición de segundo grado para la maximización del beneficio de la empresa. Por lo tanto, 4 + 24 P − 128 12 8 + 24 P + 16 q2 = 12 q1 = A su vez, las funciones de oferta individuales son relevantes para todos los precios mayores o iguales al mínimo del CVMe: ∂CVMe1 = 0 = 4q − 2 → q = 0.5 → CVMe1 (0.5) = 5.5 ∂q ∂CVMe2 CVMe2 (q ) = 2q 2 − 4q + 2 → = 0 = 4q − 4 → q = 1 → CVMe(1) = 0 ∂q CVMe1 = 2q 2 − 2q + 6 → Por lo tanto, las empresas del tipo 1 ofrecen cantidades positivas siempre que el precio sea mayor o igual a 5.5., mientras que la del tipo 2 ofrecen siempre que sea mayor o igual a 0. Si hay 8 empresas del tipo 1 y 10 del tipo 2: 8 + 24 P + 16 12 8 + 24 P + 16 4 + 24 P − 128 O = 8 xq1 + 10 xq 2 = 10 x + 8x 12 12 O = 10 xq 2 = 10 x si 0 ≤ P < 5.5 si P ≥ 5.5 7. Industria competitiva, cada empresa tiene una función de costes: C (q ) = 43.200 + 3q La demanda agregada de la industria viene dada por 2 si p > 960 ⎧0 q( p) = ⎨ ⎩19.200 − 20 p si p ≤ 960 a. p = 600; q = 100 b. CMa (q) = 6q = p → q = c. 24 empresas idénticas en la industria: O( p ) = d. p = 800; q = 3200 p 800 q 3200 = = ; π i = 10133.3 qi = = 6 6 24 24 e. p 6 24 ∑ i =1 q i = 24 p = 4p 6 3 f. g. h. i. CMe = CMa → π i = 0 43200 ∂CMe 43200 Min. CMe = + 3q → =0=− + 3 → q = 120 q ∂q q2 43200 CMe = + 3q = CMa = 6q → q = 120; p = 6.120 = 720 q 4800 q = 19200 − 20.720 = 4800 → i = = 40; π i = 0 120 8. 40 empresas competitivas e idénticas; Q = L 1/ 2 K 1 / 2 ; w = r =1; demanda de mercado viene si p > 84 ⎧0 ⎩84 − p si p ≤ 84 dada por la función q ( p ) = ⎨ a. Función de oferta de la industria a corto plazo (suponer que K =1). Q( K , L) = ( KL)1 / 2 = 1xL1 / 2 → L1 / 2 = Q →, L = Q 2 CT (Q) = CF + CV (Q) = 1 + 1xQ 2 CT (Q ) 1 + Q 2 1 = = +Q Q Q Q ∂CT (Q) = 2Q plazo = ∂Q CTME (Q) = CM (Q) corto Por la maximización de beneficios, P = CM (Q) → 2Q = P → Qi = P 2 La oferta de la industria será: O = ∑Q i = 40 i = 40 x P = 20 P 2 b. Equilibrio de la industria a corto plazo: O = 20 P = D = 84 − P → P = 4; Q = 80 , donde cada empresa producirá 2 unidades (4/2), obteniendo π i = 2 x 4 − 1 − 4 = 3 c. Equilibrio de la industria a largo plazo: El costo marginal corta al costo total medio en el mínimo: CMe(Q ) = CMa (Q ) → π i = 0 Min. CMe(Q) = ∂CMe(Q) 1 1 +Q→ = 0 = − 2 +1→ Q =1 Q ∂Q Q 1 + Q = CMa (Q) = 2q → Q = 1; P = CMa (1) = 2.1 = 2 Q 82 Q = 84 − 2 = 82 → i = = 82; π i = 2 x1 − 1 − 1 = 0 1 CMe(Q ) = 4