opamp4 - Electronica Analogica
Anuncio
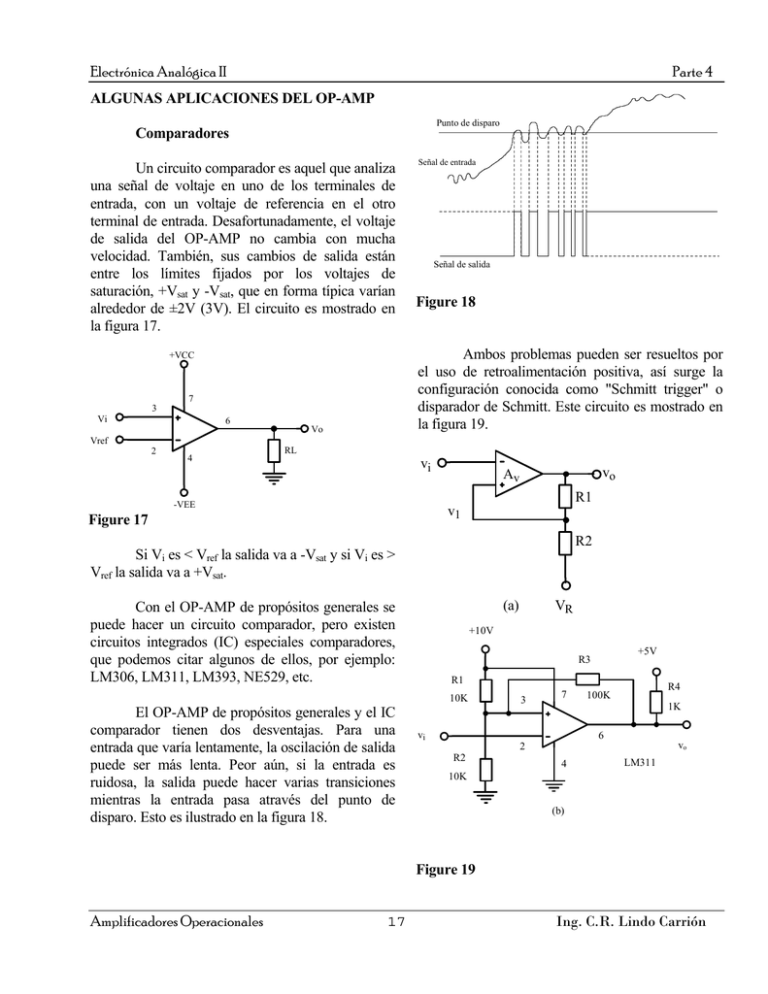
Electrónica Analógica II Parte 4 ALGUNAS APLICACIONES DEL OP-AMP Punto de disparo Comparadores Un circuito comparador es aquel que analiza una señal de voltaje en uno de los terminales de entrada, con un voltaje de referencia en el otro terminal de entrada. Desafortunadamente, el voltaje de salida del OP-AMP no cambia con mucha velocidad. También, sus cambios de salida están entre los límites fijados por los voltajes de saturación, +Vsat y -Vsat, que en forma típica varían alrededor de ±2V (3V). El circuito es mostrado en la figura 17. Señal de salida Figure 18 Ambos problemas pueden ser resueltos por el uso de retroalimentación positiva, así surge la configuración conocida como "Schmitt trigger" o disparador de Schmitt. Este circuito es mostrado en la figura 19. +VCC 7 3 Vi Señal de entrada 6 Vo Vref 2 4 RL vi vo Av R1 -VEE v1 Figure 17 R2 Si Vi es < Vref la salida va a -Vsat y si Vi es > Vref la salida va a +Vsat. (a) Con el OP-AMP de propósitos generales se puede hacer un circuito comparador, pero existen circuitos integrados (IC) especiales comparadores, que podemos citar algunos de ellos, por ejemplo: LM306, LM311, LM393, NE529, etc. +10V +5V R3 R1 10K El OP-AMP de propósitos generales y el IC comparador tienen dos desventajas. Para una entrada que varía lentamente, la oscilación de salida puede ser más lenta. Peor aún, si la entrada es ruidosa, la salida puede hacer varias transiciones mientras la entrada pasa através del punto de disparo. Esto es ilustrado en la figura 18. VR 3 7 R4 100K 1K vi 6 vo 2 R2 4 LM311 10K (b) Figure 19 Amplificadores Operacionales 17 Ing. C.R. Lindo Carrión Electrónica Analógica II Parte 4 Es un circuito regenerativo o más bien con retroalimentación positiva, es decir la tensión de entrada se aplica al terminal inversor y la tensión de retroalimentación al terminal no-inversor. umbral alto (+5) V1 (+4.76) V2 umbral bajo Este circuito es un comparador más decisivo, con histéresis, que luego será definido. entrada (+5) +Vo salida El efecto de la resistencia de retroalimentación R1 en el circuito de la figura 19(a) y R3 de la figura 19(b), es para hacer que el circuito tenga dos puntos de disparo o tensiones umbrales (threshold), dependiendo del estado de la salida. Vamos a analizar el circuito de la figura 19(a), para ello supondremos que vi es menor que v1, de modo que vo = +Vo, entonces empleando superposición, v1 = V R R1 + R 2 = (40) Vo V1 R1 + R 2 R1 + R 2 Si ahora se aumenta vi, vo permanece constante a +Vo, y v1=V1=cte hasta que vi=V1. A esta tensión umbral, crítica o de disparo la salida cambia regenerativamente a vo=-Vo y permanece en este valor mientras vi>V1. La tensión del terminal no-inversor para vi>V1 será: (0) -Vo Figure 20 Así, una entrada de ruido es menos probable que produzca múltiples disparos como se puede observar en la figura 20. La salida depende de ambos voltajes de entrada y de su historia reciente, este efecto es llamado histéresis, y su valor es calculado como la diferencia entre las dos tensiones de disparo. Para el caso del circuito de la figura 19, VH = V1 - V2. Esto puede ser ilustrado con un diagrama de la salida versus la entrada, como se muestra en la figura 21 vo (5) +Vo V1 v1 = V R R1 − R2 = Vo V 2 (41) R1 + R 2 R1 + R 2 vi Si ahora se disminuye vi, la salida permanecerá en -Vo hasta que vi se iguale a la tensión vi=V2 y la salida retorna a +Vo casi instantáneamente. Esto esta ilustrado en la figura 20. V2 (0) -Vo Figure 21 La retroalimentación positiva asegura una transición rápida a la salida sin hacer caso de la velocidad de la forma de onda de la entrada (Un pequeño capacitor "speedup" de 10 - 100 pF es conectado frecuentemente através de la resistencia Amplificadores Operacionales 18 Ing. C.R. Lindo Carrión Electrónica Analógica II Parte 4 D de retroalimentación para realzar la velocidad de conmutación aún mas). Si la señal de pico a pico fuese menor que VH, el circuito de Schmitt después de responder a la tensión umbral en una dirección, nunca se repondría de si mismo. Rf Q VS Vo El Amplificador Logarítmico y Antilogarítmico El amplificador Logarítmico (b) Figure 22 Mediante la inclusión de elementos nolineales en la red de retroalimentación, los OP-AMP se pueden utilizar para llevar a cabo operaciones no lineales sobre una o mas señales analógicas. El circuito mostrado en la figura 22(a), es un amplificador logarítmico cuya tensión de salida es proporcional al logaritmo de la señal de entrada. La inclusión de un diodo o un transistor en configuración de base común en la red de retroalimentación logra la característica logarítmica deseada para el amplificador. Los amplificadores logarítmicos son de amplia aplicación en sistemas de instrumentación, donde deben detectarse y registrarse señales de un rango muy grande. Haremos el cálculo del voltaje de salida del amplificador logarítmico, asumiendo el OP-AMP ideal, entonces: ⎛ ⎞ I = V s = I C = I s ⎜ exp V BE − 1⎟ ≅ I s exp V BE (42) R ⎝ VT VT ⎠ y Vo = - VBE Por lo tanto V o = −V T ln V s (43) IsR D I R1 VS Existen circuitos logarítmicos más precisos de alto rendimiento, con compensación de temperatura, etc. Q Vo El Amplificador antilogarítmico Para convertir a partir del logaritmo (es decir para obtener antilogaritmo) debe tomarse la exponencial del logaritmo, puesto que exp(ln x)=x. Al tomar la exponencial de un logaritmo se obtiene el antilogaritmo. Entonces usando un dispositivo logarítmico como elemento de entrada de un amplificador, se obtiene una respuesta exponencial y por lo tanto se tiene un amplificador antilogarítmico, el cual esta mostrado en la figura 22(b). (a) Amplificadores Operacionales 19 Ing. C.R. Lindo Carrión Electrónica Analógica II Parte 4 Haciendo las mismas consideraciones como en el caso del amplificador logarítmico, se tiene V o = R f I f = − R f I C (44) Nota: En los circuitos de la figura 23 y 24 se dejan fuera las constantes pertenecientes a las ecuaciones, con el objetivo de ilustrar la operación que realizan. entonces ⎛ V BE ⎞ ⎛V s⎞ ⎟ = R f I s exp⎜ ⎟ (45) ⎝VT ⎠ ⎝V T ⎠ V o = − R f I s exp⎜ donde VS es una señal logarítmica. El circuito Multiplicador y Divisor El circuito de la figura 23, es un circuito multiplicador usando OP-AMPs. En este caso se hace uso de la siguiente propiedad de los logaritmos: ln(a*b) = ln(a) + ln(b). Para el caso del divisor, mostrado en la figura 24, se hace uso de otra de las propiedades de los logaritmos: ln(a/b) = ln(a) - ln(b). R1 Q1 A3 R A1 R2 R R ln(V1) V1 Q2 ln(V2) ln(V1*V2) Rf Q3 V2 A4 VO=V1*V2 A2 Figure 23 D2 R2 V1 ln(V2) R A2 D1 R1 V2 R R A3 ln(V1/V2) ln(V1) A1 R D3 Rf A4 Vo=V1/V2 Figure 24 Amplificadores Operacionales 20 Ing. C.R. Lindo Carrión