Problemas Tema 6 - IES Alfonso X el Sabio

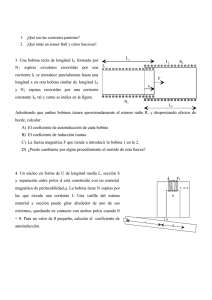
Electrotecnia. Problemas del tema 6. Inducción electromagnética
Problema 1.- Un cuadro de 400 cm 2 de sección y con 20 espiras, se encuentra situado en la
dirección normal a un campo magnético de 0.14 T y gira hasta situarse paralelamente al campo,
transcurriendo 0.25 s . ¿ Cuál es el valor de la fuerza electromotriz media inducida?
Datos .- S = 400 cm2 = 4 10-2 m2 ;;; N = 20 espiras ;;; B = 0.14 T ;;; t = 0.25 s
Determinar ξi
Resolución.- d Φ = B . d S . cos φ ; al calcular la integral Φ = -B . S . N
d
dt
=-
B. S
t
−2
.N = -
0,14 . 4 10
0,25
. 20 = - 0.448
ξi = 0.448 V
Problema 2.- Una bobina de 200 espiras y radio 0.10 m. se coloca perpendicularmente a
un campo magnético uniforme de 0.4 T . Hallar la f.e.m. inducida en la bobina si en 0.1 s:
a. Se duplica el campo magnético.
b. El campo se anula.
c. Se invierte el sentido del campo.
d. Se gira la bobina 90º en torno al eje paralelo al campo.
e. Se gira la bobina 90º en torno al eje perpendicular al campo.
Datos.- N = 200 espiras ;;; R = 0.10 m ;;; B = 0.4 T ;;; t = 0.1 s
Calcular : ξi en los diferentes casos.
S = π R2 = 3.14 . 0.12 = 0.0314 m2
Δ Φ = N (Φ2 – Φ1 )= N . B ( S2 – S1) = 0.4 0.0314 . 200 = 2,513 Wb
ξi = -
2.513
= - 25,13 V.
0.1
b. El campo se anula .- Δ Φ = N (Φ 2 – Φ1 )=N . B ( S2 – S1) = - 0.4 0.0314 . 200
= - 2,513 Wb
ξi =
2.513
= 25,13 V.
0.1
c. Se invierte el sentido del campo
Δ Φ = N (Φ2 – Φ1 )=N . B ( S2 – S1) = - 0.8 0.0314 . 200 =
- 5.026 Wb
ξi =
5.026
= 50,26 V.
0.1
d. Se gira la bobina 90º en torno al eje paralelo
En este caso Δ Φ = N (Φ2 – Φ1 )= N . B ( S2 – S1) = 0
Electrotecnia. Problemas del tema 6. Inducción electromagnética
ξi = = 0 V.
e. Se gira la bobina 90º en torno al eje perpendicular:
En este caso : Δ Φ = N (Φ2 – Φ1 )= - N B S cos 0 = - 2,513 Wb
ξi =
2.513
= 25,13 V.
0.1
Problema 3.- El conductor rectangular que aparece en la figura, de dimensiones 0.6 m y 0.3 m ,
posee una resistencia de 2,7 Ω y se encuentra situado en el interior del campo magnético B = ( 5
– y ) i (S.I.) se desplaza en la dirección del eje OY y en su sentido positivo. Sabiendo que
inicialmente el lado izquierdo del conductor rectangular coincide con el eje OZ calcular la
intensidad de corriente que circula en los casos siguientes:
a. Si se desplaza con velocidad constante de 1,5 m/s
b. Al cabo de 20 s. de comenzar su movimiento, partiendo del reposo con la aceleración de
3 m/s2.
Z
B
movimiento
Datos .- a = 0.6 m ;; b = 0.3 m ;;; R = 2.7 Ω ;;; B = (5-y) i
Calcular I.
Y
Resolución .y+0.3
Φ=
∫
y
El flujo a través de la superficie será :
y+ 0.3
y 2 ( y+0.3)
⃗
B.⃗
dS= ∫ ( 5− y ). 0.6 dy =0.6(5 y− )
=0.873−0.18 y
2 y
y
Caso a .- y = v . t ;; Φ = 0.873 – 0.18 . 1.5 . t = 0.873 – 0.27 t
ξi = Caso b
y=
d
dt
d
dt

=
R
0.27
2.7
= 0.1 A
1
a t2 , ya que se mueve con m.r.u.a. Partiendo del reposo
2
Φ = 0.873 – 0.18 .
ξi = -
= 0.27 V ;; I =
1
2
3. t2 = 0.873 - 0.27 t2
= 0.54 . t (V) ; al cabo de t = 20 s, ξi = -
I =

=
R
d
dt
10.8
2.7
= 0.54 . 20 = 10.8 V
= 4 A
Problema 4.- Un disco metálico de 20 cm de radio
gira con una velocidad de 1200 r.p.m. alrededor de un
eje axial con él . El disco se encuentra en el interior de
un campo magnético paralelo al eje de rotación y un
Electrotecnia. Problemas del tema 6. Inducción electromagnética
valor de 3 T . ¿ Qué diferencia de potencial aparecerá entre el centro y el borde del disco?
Datos .- R = 20 cm = 0.2 m. ;; ω = 1200 rpm ;;;
B = 3 T. Calcular V entre el centro y el extremo.
1
dS = R. dl
2
Resolución.1
dl . R =
2
d Φ = B . d S ;;; dS =
1
R2 dφ =
2
ω = 2 . π. (1200/60 ) = 125.66 (rd/s)
dΦ=B.
dS =
1
R2 . ω dt ; ξi = 2
2
ξi =
R B
2
=
dl=R . d ϕ
d
; en valor absoluto ξi =
dt
1 2
R . ω dt
2
d
dt
0.22 .3 .125.66
= 7.5 V
2
Problema 5.- Sobre dos rieles rectilíneos de resistencia despreciable, dispuestos
horizontalmente a 2 m. de distancia uno del otro, se
colocan dos varillas metálicas conductoras que se
pueden mover paralelamente a sí mismas,
manteniéndose en todo momento perpendicular a
los rieles. Las dos varilla son idénticas , de 3 Ω de
resistencia y 2,5 Kg de masa cada una ,
encontrándose todo el sistema en el interior de un
campo magnético uniforme de 0.5 T de inducción .
Una varilla se aleja de la otra con una velocidad de 8 m/s . Determinar la velocidad constante
que alcanza la segunda varilla sabiendo que el coeficiente de rozamiento entre las varillas y los
rieles es de μ = 0.05
Datos .- Rieles a 2 m de distancia ;;; m = 2.5 Kg ;;; R = 3 Ω ;;; B = 0.5 T
Solución :
d Φ = B . d S = B L (8 – v) d t
d
= B . L ( 8 – v) ;;; I =
dt
La fuerza que actúa sobre la varilla será :
ξi =
2
F = I .L . B =
2

=
R
B. L 8−v 
R
B . L 8−v
= μ N = μ .m . g
R
Electrotecnia. Problemas del tema 6. Inducción electromagnética
B 2 . L2 v
B 2 . L2 8
=
- μ .m . g ; Sustituyendo valores y despejando v, resulta que
R
R
v = 0.65 (m/s)
Problema 6.- Una varilla conductora AG de 0.5 m. de longitud, se apoya sobre dos raíles
CA y DG. El conjunto se encuentra situado en un campo magnético uniforme de 0.5 T,
perpendicular al plano de la figura y dirigido hacia dentro. En estas condiciones calcular:
a. La f.e.m. inducida en la varilla cuando se desplaza hacia
la derecha con una velocidad de 4 m/s.
b. La fuerza que hay que aplicar a la varilla para que siga su
B
movimiento si la resistencia del circuito es constante e igual
a 0.2 Ω .
c. La cantidad de calor desprendido por unidad de tiempo en
el circuito.
Datos .- L = 0.5 m. ;;; B = 0.5 T ;;; ξi ?? ;;; v = 4 m/s ;;; F ?? ;;; R = 0.2 Ω ;;; Q/t ??
Resolución : a. ξi = -
d
= L . v . B = 0.5 . 4 . 0.5 = 1 V
dt
b. I= I =

=
R
1
= 5 A
0.2
F = I. L . B sen α = 5 . 0.5 . 0.5 sen 90 = 1.25 N
c La potencia P = I . ξi = 5 . 1 = 5 W
Q
t
.
= 0.24 P = 0.24 . 5 = 1.2 cal/s
Problema 7.- Un alambre conductor de sección cuadrada de longitud 0.5 m, masa 20 g y
resistencia eléctrica 0.5 Ω, desliza sin rozamiento, bajando a lo largo de dos rieles paralelos de
resistencia eléctrica despreciable, inclinados un ángulo de 35º y unidos en el extremo inferior
por otro conductor como se indica en la figura, de resistencia también nula. El conjunto se sitúa
en un campo magnético vertical y ascendente de inducción 0.8 T. Determinar en estas
circunstancias el valor de la velocidad constante con que desciende dicho alambre.
Esquema :
Fm. cosα
m g sen α
Datos .- L = 0.5 m ;;; m = 20 10-3 Kg ;;; R = 0.5 Ω ;;; α = 35º ;;; B = 0.8 T ;;; v ??
Electrotecnia. Problemas del tema 6. Inducción electromagnética
d
= L . v . B cos α
dt
Resolución.- ξi = -
I= I =

=
R
FM = I. L . B =
L . v . B .cos 
R
L2 . v . B2 . cos 
R
Del equilibrio de fuerzas ( en el esquema) :
L2 . v . B2 . cos 2 
= m . g sen α
R
Fm . cos α = m. g . sen α
Por lo tanto
v =
R. m . g . sen 
2
2
2
L . B .cos 
=
0.5. 20 10−3 . 9.8. sen 35
= 0.52 m/s
0.52 . 0.82 . cos 2 35
Problema 8.-Una bobina plana MNPQ de la figura consta de 30 espiras y se encuentra
situada en el plano XOY , sometida a una inducción de 5000 Gauss perpendicular al plano y
entrante. Calcular el flujo, expresado en Wb que atraviesa cada espira de la bobina.
Cuando se invierte el sentido de inducción, en el tiempo, de 0.01 s , ¿cuál será la f.e.m.
inducida? . ¿ en qué condiciones se originará una fuerza de 1 N sobre le conductor MN de la
bobina?.
Datos .- N = 30 ;;; B = 5000 G = 0.5 T ;;; Φ ?? ;;; invierte el sentido t = 0.01 s;;; ξi ??
F = 1 N ;; condiciones.
Resolución.- d Φ = B . d S ; Φ = B X. Y . cos β = 0.5 . 0.3 . 0.15 . 1 = 0.0225 Wb
ξi = - N
d
= - 30
dt
−−
= - 30
t
F = I .L . B. N . sen β = I . 0.3 . 0.5 30 . 1 = 1 ; I =
−2. 0.0225
= 135 V
0.01
F
=
L. B. N
1
= 0.22 A
0.3. 0.5 .30
Electrotecnia. Problemas del tema 6. Inducción electromagnética
Problema 9.-Una corriente continua de 2.5 A alimenta una bobina de 500 espiras y produce un
flujo magnético de 3.6 10-4 Wb Calcular el coeficiente de autoinducción de la bobina sabiendo
que el flujo se anula después de 0.06 segundos.
Calcular la energía que se almacena .
Datos.- I = 2.5 A ;;; N = 500 ;;; Φ = 3.6 10-4 Wb;;; t = 0.06 s
Resolución .- N . Φ = L . I ;;
L =
N .
I
=
500. 3.6 10−4
= 72 mH
2.5
1
. L . I2 = 0.225 J.
2
Problema 10.- Dos bobinas, la primera de 100 espiras y la segunda de 500, se sitúan una frente a
otra . Por la primera de ellas circula una corriente de 4 A y se produce un flujo de 4 10 -4 Wb en
la primera y 2 10-4 Wb en la segunda . Calcular el coeficiente de autoindución de la primera
bobina y el coeficiente de inductancia mutua en la segunda.
E=
Datos.- NP = 100 ;;; NS = 500 ;;; IP = 4 A ;;; ΦP = 4 10-4 Wb ;;; ΦS = 2 10-4 Wb
Calcular .- L ;;; M
LP =
MPS =
Np.  p
=
Ip
100 . 4 10−4
= 10 mH
4
Ns . s
=
Ip
500. 2 10−4
= 25 mH
4