Simulación e Implementación de un esquema de Modulación Trellis

TECNIA,Vol 8 N°03, págs.11-17, 1999
Universidad Nacional de Ingeniería
Lima - Perú
Simulación e Implementación de un esquema de Modulación
Trellis-Coded y de un decodificador de Viterbi en un DSP
Reynaldo Sal y Rosas Reyes, IEEE Student Member
ABSTRACT
Tradicionalmente las técnicas de codificación/decodificación y modulación/ demodulación
para sistemas de transmisión digital fueron tratadas como instancias separadas, existiendo
un compromiso entre la potencia transmitida –que se ve aumentada si usamos un modulador
de alto orden- y el ancho de banda requerido –que se incrementa al usar codificación para la
corrección de errores-. El presente trabajo combina los criterios arriba mencionados, al
tratar en conjunto el proceso de codificación y modulación por medio de un esquema
denominado TCM (Trellis-Coded Modulation)[1]. Del mismo modo, la parte de
demodulación y decodificacion se llevan a cabo conjuntamente, por medio de un
decodificador de Viterbi basado en "soft-decision". La implementación del codificador
convolucional y del decodificador de Viterbi para la constelación 32QAM basada en la
recomendación V.32 del CCITT, se realiza en el módulo de evaluación DSP56002EVM de
MOTOROLA. La arquitectura Harvard, la flexibilidad del conjunto de instrucciones y la
velocidad del procesador digital de señales son fundamentales en la implementación.
Index terms: Trellis-Coded modulation, procesador digital de señales, codificador
diferencial, codificador convolucional, decodificador de Viterbi, distancia de Hamming,
distancia Euclidiana, constelación 32QAM.
I. INTRODUCCIÓN
Los canales de banda limitada, como los de telefonía, normalmente están expuestos a diversos tipos de
interferencia y ruido, de éstos, el ruido aditivo blanco gaussiano (AWGN) es de lejos uno de los más
perjudiciales. Tradicionalmente, las funciones de modulación y de codificación para la corrección de errores
producidos por AWGN fueron tratadas en forma separada. En el caso de la codificación para la corrección de
errores se presentaba una pérdida en la velocidad de transferencia, que era compensada incrementando el reloj
del modulador, si el canal permitía expansión del ancho de banda, o utilizando un modulador con una mayor
constelación de símbolos, si el canal era de banda limitada; esto último implicaba esquemas de modulación no
binarios (M>2). Aún así cuando la modulación y la codificación para la corrección de errores se llevaban en
forma independiente se obtenían resultados poco satisfactorios[2]. La siguiente figura ilustra mejor lo anterior.
En la figura (a) se tiene un modulador 4PSK sin codificación. En la figura (b) se añade un codificador 2/3 y se
mantiene el mismo modulador; pero se tiene que incrementar el reloj del modulador para mantener la misma tasa
de transferencia de datos, se presenta entonces un incremento del ancho de banda. Finalmente en la figura (c)
observamos el mismo codificador 2/3 y un modulador 8PSK, que evita tener que incrementar el reloj del
modulador; pero requiere una mayor constelación de símbolos.
II. Códigos de corrección de error clásicos
Para canales de ancho de banda limitado, se optaba por el esquema del tipo de la figura (1c). Como se
mencionó anteriormente, los resultados no eran los más alentadores; principalmente por dos razones:
A. Diseño de codificadores basados en la "distancia de Hamming".
B. Empleo de decodificación "hard decision".
A. Diseño de codificadores basados en la "distancia de Hamming".
El diseño de codificadores convolucionales y de bloques está clásicamente ligado al concepto de "distancia de
Hamming" o más precisamente al de "mínima distancia libre"[3]. Podemos entender por "distancia de Hamming"
al número de coordenadas en el que dos bloques de códigos (v,w) de longitud n difieren,
dHamming = d(v,w)= {i / vi¹ wi, i=0,1,..., n-1} (1)
Bajo este criterio, el decodificador recibe la señal cuantizada del demodulador sin importar cuan grande fue el
error de la señal analógica recibida. En otras palabras, el decodificador se limita a corregir los errores
introducidos por el demodulador en la toma de decisión. Es evidente que durante el proceso de decodificación
será indistinto el grado de error de la señal recibida, produciéndose una pérdida irreversible de infomación. Este
tipo de decodificación se conoce como "hard decision".
B. Empleo de decodificación "hard decision"
Existen diferentes tipos de métodos para decodificar códigos convolucionales, entre los que destacan el
secuencial, el threshold y el propuesto por Viterbi en 1967. Como se ha podido ver, tradicionalmente el
decodificador actuaba sobre los datos cuantizados por el demodulador privándose de valiosa información que
podría ser utilizada sí el decodificador actuara sobre la data no cuantizada, en otras palabras, si realizara el
proceso de demodulación y decodificación en forma conjunta. Este esquema de decodificación se denomina
"soft decision" y esta estrechamente ligado al concepto de "distancia euclidiana" en la modulación Trellis-Coded.
Para dos bloques de códigos (v,w) de longitud n, la "distancia euclidiana" será:
dEuclidiana={(v0-w0)2 +(v1-w1)2 +...+(vn-1-wn-1)2 }0.5 (2)
Aún usando un decodificador de Viterbi "soft decision" en lugar de uno "hard decision" el rendimiento global del
sistema no mejora ostensiblemente. Esto se debe a que no existe una relación directa entre la "distancia de
Hamming" y la "distancia Euclidiana", sin importar como se distribuyan los puntos en la constelación. Queda
claro entonces que el diseño de codificadores convolucionales debe basarse en la "distancia Euclidiana" en lugar
de la "distancia de Hamming", como lo propuso Ungerboeck. La siguiente figura nos muestra el concepto de
"distancia euclidiana" en un esquema de modulación 4PSK.
figura 2
En la figura (2) se observa que la "distancia euclidiana" d1 corresponde a los puntos p1 y a las coordenadas de
00, de la misma forma la "distancia euclidiana" d2 corresponde a los puntos p2 y a las coordenadas de 00.
III. Trellis-Coded Modulation
El TCM propone la elección adecuada de un esquema de modulación y codificación convolucional -basados en
la "distancia euclidiana" y la búsqueda de los correspondientes polinomios de chequeo de paridad -, y la
realización del proceso de demodulación y decodificación en un solo paso, sin implicar ello un incremento en el
ancho de banda del sistema.
Los esquemas TCM más sencillos (cuatro estados) pueden mejorar en 3dB la ganancia total del sistema,
mientras que los más complejos pueden sobrepasar los 6dB.
A. Constelación
Las constelaciones multinivel existentes optimizadas para "distancia de Hamming" no garantizan una buena
esctructura de "distancia euclidiana", por lo que se hace necesario la búsqueda de nuevas constelaciones y
nuevos códigos para TCM. Las primeras constelaciones, propuestas por Ungerboeck se obtuvieron
optimizando a mano las ya existentes. En la actualidad se han podido encontrar esquemas con mayor ganancia
mediante el empleo de algoritmos genéticos[4], quedando claro que las constelaciones asimétricas presentan en
TCM mejor ganancia que las ampliamente usadas y conocidas constelaciones simétricas (8PSK, 32QAM, etc.).
La figura (3.a) muestra una constelación 8AM simétrica mientras que la figura (3.b) muestra una 8AM
asimétrica.
Figura(3)
La figura (4) muestra la constelación simétrica 32QAM de la norma V.32 del CCITT, utilizada en la
implementación realizada. Se muestran también las 52 regiones existentes que corresponden a la superposición
de las regiones pertenecientes a cada uno de los estados del codificador –ocho estados en total-.
Figura(4)
B. Codificación TCM.
La figura (5) muestra el sistema de codificación diferencial y convolucional también para la norma V.32 del
CCITT. Al igual que la constelación 32QAM los codificadores han sido implementados en un DSP.
Figura(5)
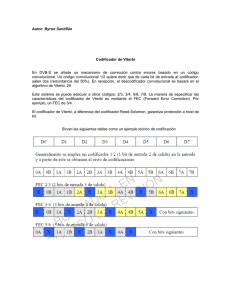
Los datos paralelos Q1n y Q2n son las entradas del codificador diferencial, que se encargará de proporcionar 90
grados de invarianza de fase; es decir, Q3n y Q4n serán los mismos para puntos en la constelación 32QAM que
se encuentren a 90 grados uno de otro. La figura (6) nos muestra la implementación del codificador diferencial y
la correspondiente tabla de entrada, salida y estados; mientras que la figura (7) muestra el diagrama de Trellis del
codificador convolucional.
Figura(6)
Input bits
Past Output
bits
Output bits
Q1n
Q2n
Y1n- Y2n-1 Y1n
1
Y2n
0
0
0
0
0
0
0
0
0
1
0
1
0
0
1
0
1
0
0
0
1
1
1
1
0
1
0
0
0
1
0
1
0
1
0
0
0
1
1
0
1
1
0
1
1
1
1
0
1
0
0
0
1
0
1
0
0
1
1
1
1
0
1
0
0
1
1
0
1
1
0
0
1
1
0
0
1
1
1
1
0
1
1
0
1
1
1
0
0
0
1
1
1
1
0
1
Figura (7)
Es importante observar en la figura que los estados pares provienen de los estados anteriores 0, 1, 2 y 3;
mientras que los estados impares provienen de los estados anteriores 4, 5, 6 y 7. Este hecho permitirá reducir
significativamente el código en lenguaje ensamblador utilizado en el decodificador.
IV. Decodificación TCM.
El proceso de decodificación V.32 comprende la implementación del decodificador de Viterbi y del
decodificador diferencial, tal como lo muestra la figura (8).
Figura(8)
A. Decodificación por medio del Algoritmo de Viterbi.
De los algoritmos de decodificación de códigos convolucionales existentes, el de Viterbi demuestra ser el mejor
para cierto tipo de aplicaciones. La elección de un algoritmo entre los otros, dependerá de la eficiencia del
mismo y de la conplejidad de su implementación. El algoritmo de Viterbi es asintóticamente óptimo; pero su
complejidad crece en forma exponencial conforme es mayor el "constraint length" del código. En nustro caso el
codificador convolucional tiene un "constraint lenght" de cuatro (K=4), lo que hace realizable la implementación
del algoritmo de Viterbi. Típicamente los decodificadores de Viterbi están limitados a "constraint lenght" de
valores menores que diez; mientras que los decodificadores secuenciales son eficientes hasta valores cercanos a
50.
El algoritmo de Viterbi usa la estructura del trellis del codificador convolucional, para determinar la ruta óptima a
la salida de éste. Existen 2 métodos de obtener dicha salida: Traceback y register exchange. Ambos métodos
requieren una cantidad de memoria similar; la diferencia entre ellos radica en la mayor velocidad y complejidad
del traceback .
V. Simulación e Implementación.
Los diagramas de flujo de los sistemas de codificación y decodificación se muestran en las figuras (9) y (10). Es
evidente que el tiempo de procesamiento del decodificador es mayor que el del codificador, debido a su mayor
complejidad, y por consiguiente a la mayor cantidad de rutinas a ejecutar. Se requirió calcular las 52 fronteras
existentes en la constelación por medio de un programa en MATLAB basado en el concepto de "distancia
euclidiana".
La simulación de ambos sistemas se realizó mediante el software "DSP56000 Simulator" -fig(11)proporcionado por MOTOROLA; se comprobó el funcionamiento global del sistema mediante el siguiente
procedimiento: Se generó una secuencia aleatoria en MATLAB que fue usada como entrada del codificador; la
salida fue contaminada con AWGN y fue usada como entrada del decodificador, comparándose finalmente la
secuencia original de entrada con la de salida, y verificándose la capacidad de corrección de errores del sistema.
La implementación se realizó en el módulo de evaluación DSP56002EVM[6,7], las pruebas a cada sistema se
llevaron a cabo por separado, restando la transmisión de la data por un medio físico; para ello se está realizando
la programación del SSI y del codec de la tarjeta. Los próximos avances estarán referidos a la implementación
de una interface serial PC-DSP bajo un sistema operativo en tiempo real (Real Time Linux[8]).
Figura(9)
Figura(10)
Figura(11)
VI. Agradecimientos
El presente trabajo no se hubiera podido realizar sin el apoyo de la Sección de Post Grado y Segunda
Especialización de la Facultad de Ingeniería Elécrtica y Electrónica de la UNI en la persona del Dr. Arturo Rojas
Moreno.
VII. Referencias
[1] G. Ungerboeck, "Channel coding with multilevel/phase signals," IEEE Trans. Information
Theory, vol. IT-28, pp. 55-67, Jan. 1982.
[2] G. Ungerboeck, "Trellis-Coded Modulation with Redundant Signal Sets," IEEE
Communications Magazine, vol. CM-25, pp. 5-21, Feb. 1987.
[3] Stephen B. Wicker, Error Control Systems for Digital Communications and Storage.
[4] René J. Van der Vleuten and Jos H. Weber, "Optimized Signal Constellations for TrellisCoded Modulation on AWGN Channels," IEEE Trans. on Communications, vol. TC-44,
pp 646-648, Jun. 1996.
[5] Ezio Biglieri, Dariush Divsalar, Peter McLane, Marvin Simon, Introduction to Trellis-Coded
Modulation with Application.
[6] MOTOROLA, DSP56002 User Manual.
[7] MOTOROLA, DSP56000 Family Manual.
[8] RTLINUX, http://www.rtlinux.org
[9] MOTOROLA, application notes.
Para mayores referencias diríjase a la siguiente dirección
igi@uni.edu.pe