Imprimir este artículo

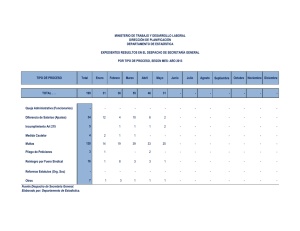
91
Aplicación de Programación Lineal para Definir el Despacho de
Unidades Generadoras Hidroeléctricas
Mario E. López Acosta ¹, Esteban F. Vargas Correa ², Anastacio S. Arce Encina 3
Facultad Politécnica, Universidad Nacional del Este
Ciudad del Este, Paraguay
1
mariote06@gmail.com, 2efvargasc@fpune.edu.py, 3 sebastian_arce@fpune.edu.py
Resumen. El despacho de unidades generadoras hidroeléctricas define el número de máquinas que serán
comprometidas para atender la demanda a cada intervalo de tiempo. Este trabajo presenta un modelo de despacho de
unidades generadoras hidroeléctricas, que adopta como criterios de desempeño el caudal turbinado hora a hora, el
número de arranques y paradas de unidades generadoras y la combinación de los criterios anteriores, llevando en
cuenta el costo de los arranques y paradas de las unidades generadoras y el valor del volumen de agua ahorrado a
través del despacho. El problema del despacho de unidades generadoras se caracteriza como un problema de
programación mixta entero-no lineal y combinatorio, cuya solución puede complicarse en la medida que el número
de unidades generadoras disponibles aumenta. En este trabajo se propone una metodología de solución para obtener
una configuración de máquinas mediante la aplicación de Programación Lineal.
Palabras Claves: Despacho de unidades generadoras, minimización del caudal turbinado, minimización de
arranques y paradas, minimización multiobjetiva, programación lineal, usinas hidroeléctricas.
Abstract. The hydroelectric generating units dispatch is responsible for defining the number of machines that are
committed to meet the current demand. This work presents a hydroelectric generating units dispatch model that
takes into account the hourly water-flow through the turbines, the number of hydroelectric generating units starts
and stops, these same quantities combined with their start and stop costs and the saved water volume value in the
dispatch. The hydroelectric generating units dispatch is configured as a combinatorial integer-nonlinear mixed
problem. This problem solution complexity grows with the number of generating units. This work proposes a
solution methodology to get a machine configuration through a linear programming application.
Keywords: flow minimization, start and stop minimization, multi objective optimization, linear programming,
hydroelectric plants.
1. Introducción
2. Criterio de Desempeño
En los últimos años, varios trabajos realizados
enfocaron sus estudios en el planeamiento de la
operación de corto plazo considerando sistemas
predominantemente hidroeléctricos, donde la decisión
del número de unidades generadoras en operación a lo
largo del día y sus respectivos puntos de operación,
tienen fuerte influencia sobre la eficiencia del sistema.
El criterio de desempeño adoptado en los sistemas de
generación termoeléctrica fundamentalmente está
relacionado al costo del combustible utilizado en la
producción y en el proceso de arranque y parada de las
unidades generadoras. En los sistemas de generación
hidroeléctrica tales criterios de desempeño no se
aplican ya que no existe un costo directo asociado al
uso del agua ni un estudio concluyente sobre el costo
asociado a los arranques y paradas de las unidades
hidroeléctricas.
El número de unidades generadoras necesarias para
atender la carga, varía conforme varía la carga a lo
largo del día. Por la variación de número de unidades
generadoras a ser despachada para satisfacer la
demanda, surge la posibilidad de adoptar y optimizar
un criterio de desempeño.
La función de producción de una unidad generadora
hidroeléctrica es dada por la siguiente ecuación:
P = ρ × g × ntur × ng × h × q ×10−6 (MW)
[1]
Donde: ρ es el peso específico del agua; g la
aceleración de la gravedad;
ntur y n g
son los
rendimientos de la turbina y del generador,
respectivamente; h es la altura del salto neto; q es el
caudal turbinado; P es la potencia generada por una
unidad generadora.
ELÉCTRICA - Nº 5 – AÑO 2009
92
El rendimiento de la turbina hidráulica
ntur
es una
función no lineal que depende del caudal turbinado y
de la altura de salto. Para una dada altura del salto neto
y aumentando el caudal turbinado desde el límite
inferior hasta el límite superior de la zona de operación
normal, se puede verificar que el rendimiento aumenta
hasta alcanzar un valor máximo para luego disminuir
nuevamente. La producción con mayores valores de
rendimiento resultará en un mejor aprovechamiento del
recurso hídrico obteniendo la misma producción
energética para un volumen inferior de agua turbinado.
En la figura 1 se muestra el rendimiento de una turbina
tipo Francis.
η
El rendimiento del generador g a su vez presenta
variaciones menores. La curva de la figura
igura 2 muestra
una saturación próxima a los valores nominales, por lo
que puede ser considerado el rendimiento del
generador como una constante.
Fig. 1 Rendimiento de una turbina tipo Francis
cuantificar el valor de un arranque o parada de una
unidad hidroeléctrica. En este trabajo será utilizado
como referencia el valor estimado en [3], el cual
establece que cada parada o arranque tiene un costo
equivalente a 3,0 US$ por MW de potencia nominal de
la unidad generadora.
2.2 Caudal Turbinado
El despacho que maximiza la eficiencia buscará
alcanzar la meta de producción con el menor consumo
del recurso hídrico. De la figura
igura 1, se puede deducir
que para cada valor de altura del salto
salt neto existe un
valor ideal de caudal a ser turbinado para obtener el
mejor rendimiento. Por ejemplo, para una altura de
salto en la línea del punto A, se puede verificar que la
producción de una unidad generadora turbinando 600
m3/seg será diferente de laa producción de dos unidades
generadoras cada una turbinando 300 m3/seg, debido al
rendimiento. Este mismo raciocinio se aplica a la
generación de un mismo valor de potencia con
diferentes números de unidades generadoras, es decir,
existe un número ideal dee unidades generadoras
asociado para cada valor de salto y potencia a ser
generada. La figura 3, muestra el resultado de este
raciocinio para diferentes valores de salto bruto y
potencia a ser generado. Las curvas que separan las
fajas de generación de los diferentes números de
unidades generadoras en función al salto bruto pueden
ser utilizadas como guías para la minimización del
caudal turbinado [2]. Como ejemplo de aplicación,
considere la demanda de 5.000 MW y el salto bruto de
115 metros. Conforme a lass curvas de la figura 3, el
número óptimo de unidades generadoras que minimiza
el caudal turbinado es nueve.
Fig. 2 Rendimiento del generador
2.1 Arranques y Paradas de Unidades Generadoras
El proceso de arranques o paradas de las unidades
generadoras hidroeléctricas, diferentemente a las
termoeléctricas, es rápido y prácticamente sin ningún
costo. Existe sin embargo algunos aspectos como los
riesgos de una eventual falla que puede ocurrir tanto en
el proceso de arranque o parada, que dejaría la unidad
indisponible para operar, y las cconsecuencias
económicas asociadas a la misma. Así también existen
los desgastes de los componentes mecánicos, eléctricos
y equipos de control asociados a los frecuentes
arranques y paradas. A pesar de los inconvenientes
citados no existe un estudio concluyente
ente que permita
Fig. 3 Curvas de número de máquinas con menor caudal
turbinado
3. Formulación Matemática
El problema del despacho de unidades
unid
generadoras,
tomando como criterio de desempeño el caudal
ELÉ
ELÉCTRICA - Nº 5 – AÑO 2009
93
turbinado y el número de arranques y paradas, puede
ser representado por la siguiente formulación:
11
10
[
Min ∑ c q (nt , ht , Pt ) + c
p
AP
nt − nt −1
]
[2]
t =1
S.a.
nt (Pt , ht ) ≤ nt ≤ nt (Pt , ht )
[3]
Pt (nt , ht ) ≤ Pt ≤ Pt (nt , ht )
[4]
n∈ N
[5]
Donde: T es el horizonte de programación;
potencia generada;
Pt es la
nt es el número de máquinas en
operación en el intervalo t; q() es la función que
representa el caudal turbinado total; C P es el valor del
volumen del agua turbinado; C AP es el costo de
arranques y paradas de máquinas, nt ( Pt , ht ) y
nt ( Pt , ht ) representan el número mínimo y máximo
de unidades generadoras que pueden entrar en
operación, representa la potencia mínima Pt (nt , ht ) y
máxima
Pt (nt , ht ) asociado a nt unidades
generadoras. Finalmente la ecuación (5) define que la
variable n pertenece al conjunto de números naturales.
El problema de despacho de unidades generadoras
formulado de esta manera se caracteriza como un
problema de programación mixta entero-no lineal y
combinatorio, cuya solución puede complicarse en la
medida que el número de unidades generadoras
disponibles aumenta. Esto no impide que el problema
sea resuelto por Programación Lineal.
10 10
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
9
9 9
9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9
8
8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8
7
7 7 7 7 7 7 7 7 7 7
Número de Máquinas
T
6
6 6 6 6 6 6 6
5
5 5 5 5 5
8
4
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
Hora
Fig. 4 Configuración de máquinas posibles
La figura 4 puede ser representada en forma de grafos,
en el cual cada número de máquinas puede ser
considerado como un nodo y los arcos que unen los
nodos representan las posibles transiciones de un
estado, caracterizado por un cierto número de
máquinas despachadas, para otro estado o
configuración de máquinas del siguiente horario. En
cada nodo es asociado el caudal turbinado total por el
número de máquinas correspondiente al nodo para
atender la generación programada.
A través del grafo es posible formular
matemáticamente el problema para resolverlo mediante
programación lineal, en el cual las variables
representan las trayectorias posibles a seguir. En la
figura 5, se representa un grafo con dos nodos y sus
arcos.
4. Metodología Aplicada
Fig. 4 Representación del grafo
Para poder formular el problema del despacho de
unidades generadoras hidroeléctricas y resolverlo
mediante programación lineal, es necesario definir
antes que nada los números mínimo y máximo de
unidades generadoras capaces de atender la demanda y
que operen dentro de los límites permitidos de
turbinamiento para cada hora del día. Una vez obtenido
los números mínimo y máximo de máquinas, es posible
obtener todas las posibles configuraciones de máquinas
factibles a despachar. En la figura 4, se observa todas
las posibilidades de despacho para una cierta
generación programada.
Donde:
C jk = ( q j + q k )
[6]
Para el caso de minimización del caudal turbinado.
[7]
C jk = j − k
Para el caso de minimización de arranques y paradas, y
para ambos caso:
nt ≤ j ≤ nt
[8]
nt +1 ≤ k ≤ nt +1
[9]
Para el caso de la minimización multiobjetiva, deberán
ser asignados valores monetarios al volumen de agua
economizada en el despacho, para comparar con el
costo de los arranques y paradas.
Para valorizar la economía de agua, será tomada como
referencia el resultado del despacho que minimiza el
ELÉCTRICA - Nº 5 – AÑO 2009
94
caudal turbinado. En este sentido cuando el despacho
de unidades generadoras coincide con el despacho que
minimiza el caudal turbinado no se habrá incurrido en
ninguna pérdida de agua. Caso contrario si el despacho
no coincide con la minimización del caudal turbinado,
está perdida será valorizada por la siguiente expresión:
∆Pjk = ρ × g × ng × nk × hk × ∆qk
[10]
∆qk = qkop − qk
[11]
considera las transiciones de máquinas de una hora a
otra, así como toma la ecuación (7), y las restricciones
del problema están dadas a continuación:
F .O. = 1x 20, 3 + 2 x 20, 4 + 1x31, 4 + 2 x13,5 + 3 x31, 6 + 0 x14, 4 + 1x14 , 5
+ 2 x14, 6 + 1x42, 3 + 0 x 42, 4 + 1x 42, 5 + 2 x52, 3 + 1x52, 4 + 0 x52, 5 + 3 x62, 3
+ 2 x62, 4 + 1x62, 5 + 0 x33, 3 + 1x33, 4 + 2 x33, 5 + 1x 43,3 + 0 x43, 4 + 1x43, 5
+ 2 x53, 3 + 1x53, 4 + 0 x53, 5 + 1x34, 4 + 0 x 44, 4 + 1x54, 4
Donde:
S .a
1 = x 20, 3 + x 20, 4
x 20, 3 = x 31 , 4 + x 31 , 5 + x 31 , 6
∆q k
representa la diferencia entre el caudal turbinado
en la hora k y el caudal óptimo turbinado en la misma
hora k.
En este caso el gasto que representa el problema en la
figura 5 esta dado por la siguiente expresión:
[12]
C jk = C P ∆Pjk + C AP j − k
En cuanto a las restricciones del problema, para los tres
objetivos, son las mismas. Las restricciones se obtienen
analizando los arcos que entran y salen en cada nodo,
la suma de todos los arcos que entran al nodo es igual a
la suma de todos los arcos que salen del mismo.
Para mayor comprensión de la metodología aplicada a
continuación se ilustra un simple ejemplo del problema
de despacho de unidades generadoras.
En la figura 6, se observa el grafo obtenido para cuatro
intervalos de una cierta demanda programada con un
nodo inicial y final. Del grafo se puede obtener la
función objetivo y las restricciones del problema.
x 20, 4 = x 14 , 4 + x 14 , 5 + x 14 , 6
x 31 , 4 + x 14 , 4 = x 42, 3 + x 42, 4 + x 42, 5
x 31 , 5 + x 14 , 5 = x 52, 3 + x 52, 4 + x 52, 5
x 31 , 6 + x 14 , 6 = x 62, 3 + x 62, 4 + x 62, 5
x 42, 3 + x 52, 3 + x 62, 3 = x 33, 3 + x 33, 4 + x 33, 5
x 42, 4 + x 52, 4 + x 62, 4 = x 43, 3 + x 43, 4 + x 43, 5
x 42, 5 + x 52, 5 + x 62, 5 = x 63, 3 + x 63, 4 + x 63, 5
x 33, 3 + x 43, 3 + x 53, 3 = x 34, 4
x 33, 4 + x 43, 4 + x 53, 4 = x 44, 4
x 33, 5 + x 43, 5 + x 53, 5 = x 54, 4
x 34, 4 + x 44, 4 + x 54, 4 = 1
En la Tabla 1, se resume la configuración de máquinas
resultante, número total de transiciones y caudal
turbinado total para el periodo analizado.
Tabla 1. Resultado obtenido del despacho A/P
t=1
Nº de
Máquinas
t=2
3
4
t=3
4
t=4
4
Cantidad
de A/P
1
Caudal
turbinado total
(m 3 / seg )
8354
Para la minimización del caudal turbinado y
multiobjetiva las restricciones del problema son las
misma, solo cambia la función objetivo para cada caso.
5. Resultados
Fig. 5 Grafo de número de máquinas
La función objetivo para el caso de minimización de
arranques y paradas de máquinas, en el cual se
La metodología propuesta fue aplicada a la central
hidroeléctrica de Itaipu. Para el efecto fueron
considerados el programa de generación de un día
domingo y la disponibilidad de 10 unidades
generadoras. Los datos del programa de generación
están registrados en la Tabla 2. De estos datos se
obtuvo todas las posibles configuraciones de despacho
que respetan los rangos permitidos de operación, como
ELÉCTRICA - Nº 5 – AÑO 2009
95
El número de restricciones es igual a la cantidad de
nodos y la cantidad de variables es igual a la cantidad
arcos. Por la gran cantidad de variables y restricciones,
es necesario resolver el problema con ayuda de algún
solver, para eso fue utilizado la función linprog del
Matlab 7.0.
Los resultados obtenidos son vectores que representan,
para cada hora con valores distinto de cero, cual es el
camino a tomar en el grafo que minimiza el objetivo.
comparación a la configuración obtenida por las curvas
de números de máquinas con menor caudal turbinado.
11
10
9
Nº Máquinas
mostrado en la figura 4, en el cual se obtiene 80 nodos,
contando un nodo inicial y final, y 263 arcos en total.
8
7
6
5
4
Tabla 2. Generación programada
1
H
Pot.[MW]
H
Pot.
[MW]
H
Pot.
[MW]
H
Pot.
[MW]
H
Pot.
[MW]
H
Pot.[MW]
1
4749
5
3682
9
4650
13
5300
17
5328
21
6068
2
4217
6
3659
10
5264
14
5303
18
5772
22
2
3
4
5
6
3694
7
3633
11
5289
15
5317
19
5971
23
5418
4
3682
8
4141
12
5301
16
5326
20
6109
24
5438
8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
Hora
6000
3
7
Conf. PL
Conf. OP
Nº Min
Nº Max
Fig. 6 Despacho por minimización del caudal turbinado
5.2 Minimización de Arranques y Paradas de
Máquinas
5.1 Minimización del Caudal Turbinado
Para poder verificar la factibilidad de la metodología
aplicada fue utilizada la tabla de la figura 3, con el cual
se obtiene una configuración óptima de máquinas que
minimiza el caudal turbinado, para poder comparar con
la solución de la función linprog. Los resultados se
pueden verificar en la Tabla 3. Los valores obtenidos
en la columna OP se refieren a los resultados obtenidos
a través de la figura 3 y los datos de la columna PL se
refieren a los resultados obtenidos a través de
programación lineal. Comparando los resultados se
puede verificar una mínima diferencia entre las dos
metodologías.
Para este estudio de caso, se utilizaron los mismos
datos de generación programada dados en la Tabla 2.
Observando detenidamente la figura 4 es posible notar
más de una configuración de máquinas que resulte en
un mismo número de arranques o paradas al final día.
La solución obtenida por la función linprog especifica
todas estas posibles configuraciones de máquinas. En
la figura 8, se observan los arcos posibles obtenidos,
que representan las variables del problema, con sus
respectivos valores que equivalen al peso de
seleccionar un arco que parte de un cierto nodo. En la
figura 9, se muestra una configuración obtenida por la
PL el cual resultó en dos arranques, considerando el
número inicial de máquinas.
Tabla 3. Configuración óptima y configuración PL
H
Conf.
OP.
Conf.
PL
H
Conf.
OP.
Conf.
PL
H
Conf.OP.
Conf.
PL
1
8
8
9
8
8
17
9
9
2
7
7
10
9
9
18
10
9
3
6
6
11
9
9
19
10
9
4
6
6
12
9
9
20
10
10
5
6
6
13
9
9
21
10
10
6
6
6
14
8
8
22
10
10
7
6
6
15
8
8
23
9
9
8
7
7
16
9
9
24
10
10
En la Figura 6, se muestra las configuraciones de
máquinas obtenidas y el número mínimo y máximo de
máquinas posibles de atender a la demanda
programada. Se puede apreciar que la configuración
obtenida por la programación lineal se encuentra
dentro del intervalo de número mínimo y máximo de
máquinas y se diferencia en tan solo dos puntos en
Fig. 7 Soluciones de configuración obtenida
ELÉCTRICA - Nº 5 – AÑO 2009
96
Tabla 5. Prueba con diferentes costos
11
Costo
Arranque/Paradas
[US$]
Costo de
energía
[US$/MWh]
Nº de
Arranques
y paradas
Caudal
turbinado
[m3/seg]
Variación
de caudal
turbinado
[m3/seg]
9
1800
50
6
110.012
71
8
2100
30
4
110.055
186
7
2500
20
2
110.465
241
Nº Máquinas
10
6
6. Conclusión
5
4
1
2
3
4
5
6
7
8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
Hora
Nº Min
Nº Max
Configuracion A/P
Fig. 8 Despacho por Minimización de Arranques-Paradas de
máquinas
Este trabajo presenta un modelo para el Despacho de
Unidades Generadoras Hidroeléctricas que utiliza
como criterio de desempeño la minimización de
arranques y paradas y el caudal turbinado. Como
metodología de solución aplica Programación Lineal
Los estudios de casos, utilizando datos del programa de
generación de un día domingo apuntan que:
•
La optimización del despacho que minimiza el
caudal turbinado acompaña la variación de la
carga y resulta en frecuentes arranques y paradas.
•
La optimización del despacho que minimiza el
número de arranques y paradas resulta en un alto
valor de caudal turbinado al final del día.
•
Para determinar el despacho óptimo, desde el
punto de vista económico, es fundamental
determinar principalmente cuánto cuesta un
arranque o parada.
5.3 Minimización Multiobjetiva
En este estudio, serán considerados los costos de
arranques y paradas y el valor de volumen de agua
turbinado, buscando de esta manera obtener una
solución de compromiso entre los dos objetivos. El
valor atribuido al costo de arranques y paradas es una
extrapolación a los costos asociado a los arranques y
paradas encontrados en [3]. El valor atribuido al
volumen de agua turbinado es equivalente a la energía
posible de ser generada por el mismo. En la Tabla 3, se
sintetizan los resultados del despacho para diferentes
valores de costos en término de caudal turbinado,
número de arranques-paradas y variación de caudal
turbinado, que representa el volumen de agua perdido
al final del día.
Tabla 4. Resumen del despacho para los 3 objetivos
Costo
Arranque/Paradas
[US$]
Costo de
energía
[US$/MWh]
Nº de
Arranques
y paradas
Caudal
turbinado
[m3/seg]
Variación
de caudal
turbinado
[m3/seg]
0
30
10
109.980
0
2100
0
1
110.902
218
2100
30
4
110.055
186
En la Tabla 4, puede ser constatado que la
minimización multiobjetiva resulta en valores
intermedios en términos de caudal turbinado y número
de arranques o paradas de máquinas. En la Tabla 5, se
realiza un análisis de sensibilidad y se demuestran los
resultados obtenidos para diferentes valores del agua y
de arranques y paradas.
Finalmente se puede concluir que, por más que el
problema del despacho de unidades generadoras
hidroeléctricas se caracterice por ser un problema de
programación mixta-entero no lineal, es posible
obtener una solución a través de Programación Lineal.
Referencias
[1] Arce, A.; Ohishi, T.; Soares, S. “Optimal Dispatch
of Generating Units of the Itaipu Hydroelectric
Plant”, IEEE Transactions on Power Systems, Vol.
17, pp. 154-157, 2002
[2] López, M.; Arce, A. “Aplicación de Algoritmos
Genéticos para Definir el Despacho de Unidades
Generadoras Hidroeléctricas”. In: Seminario Del
Sector Eléctrico Paraguayo- CIGRE Paraguay,
Octubre 2008.
[3] Nilsson, O.; Sjelvgren, D. “Hydro unit start-up
costs and their impact on the short term scheduling
strategies of swedish power producers”, IEEE
Transactions on Power Systems, vol. 12, no. 2,
pp.38-43, 1997.
[4] Programa
Diario
de
la
Operación,
OP.DT/OPS.DT/OPSP.DT, Itaipu Binacional,
23/03/200
ELÉCTRICA - Nº 5 – AÑO 2009