cálculo II etsiccpc
Anuncio

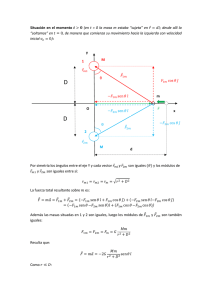
cálculo II etsiccpc práctica 3, EDOs de orden n curso 2009/10. (fecha de entrega 23/11/09) 1.- Integrar la ecuación diferencial 4 y′′ + 4 y′ + y = ∞ ∑e −x 2 sin nx n =1 a) La solución particular se obtendrá por el método de los coeficientes indeterminados b) La solución particular se obtendrá por los métodos operacionales de Heaviside c) Comprobar que ambas soluciones son iguales (junio 2009) 2.- Resolver y′′′ + 3 y′′ + 3 y′ + y = sin x (1er parcial 2009, 1/5 de ejercicio) 3.- Sea L(D) un operador diferencial polinómico de coeficientes constantes L(D ) = an D n + an−1 D n−1 +···+ a2 D 2 + a1 D + a0 , con n raíces reales y simples r , r ,..., r , donde D 1 2 n es el conocido operador derivada. Con an , an−1 ,..., a1 , a0 , a , constantes reales y f(x) una función real de variable real, se pide demostrar las siguientes expresiones en caso de que sean ciertas. 1 ax e ax e = L (D ) L(a ) 2 2 b) L D sin ax = L − a sin ax a) ( ) ( ) c) D (e f (x )) = e (D + a ) f (x ) 2 ax 2 ax (1er parcial 2009, 1/5 de ejercicio) 4. Resolver la ecuación diferencial (1 − x )(xyy′′ − yy′ − xy′ ) = 2 x 4 2 4 yy′ mediante el cambio de variable t = x2 v = ln y (1er parcial 07) 5.- Muchos problemas de cálculo de estructuras se pueden resolver mediante la aplicación de la conocida segunda ley de Newton que supone igualar la resultante de las fuerzas actuantes a la variación de la cantidad de movimiento del sistema mecánico. ∑F = d (mv ) dt Dado que en general, en los problemas de estructuras la masa se puede considerar constante en el tiempo, y que además el sistema mecánico está en reposo, la segunda ley de Newton se limita a verificar que la resultante de fuerzas es nula. ∑F = 0 En el cálculo de fluidos es también necesario que se verifique la segunda ley de Newton sobre un sistema mecánico de naturaleza líquida o gaseosa que en general va a estar en movimiento, lo cual conduce a lo que se conoce como ecuación dinámica. Pero además, en fluidos se hace necesario introducir una ecuación adicional que asegure la conservación de la masa (ecuación de continuidad), ya que la sustancia que se está considerando cambia de forma de manera ostensible. Se tendrá que asegurar por tanto que en ausencia de fuentes y sumideros la masa dentro de un cierto volumen de control se conserva. d (mv ) ∑ F = dt ∑M = 0 Para fluidos incompresibles dichas ecuaciones se pueden expresar como ∂ 2u ∂ 2u ∂ 2u ∂ui ∂u ∂u ∂u 1 ∂p + u1 1 + u2 2 + u3 3 = f i − + ν 2i + 2i + 2i ∂z ∂t ∂x ∂y ∂z ∂y ρ ∂xi ∂x ∂ui =0 ∂xi conocidas como ecuaciones de Navier-Stokes, y cuyas incógnitas son el campo de velocidades ui y las presiones del flujo p. Si se considera la variación de una cantidad φ de una determinada sustancia transportada por efecto de la convección y la difusión en un cierto medio líquido unidimensional, las ecuaciones vectoriales anteriores se pueden reducir a una ecuación escalar en derivadas parciales que en ocasiones se denomina ecuación del transporte o ecuación de convección difusión y que en su forma unidimensional se puede escribir como ∂φ ∂φ ∂ ∂φ +U − k = Q(x ) ∂t ∂x ∂x ∂x que para el caso del flujo permanente puede ser expresada como la ecuación diferencial ordinaria U dφ d 2φ − k 2 = Q(x ) dx ∂x (1) donde el primer término es el convectivo, el segundo el difusivo y el tercero es el término fuente. En lo que sigue se va a suponer que tanto la velocidad U, como el coeficiente de difusividad k son constantes y que el término fuente Q(x) es una función que depende exclusivamente de la variable independiente x. Se pide: a) Resolver la ecuación diferencial homogénea asociada a (1) b) Obtener la solución particular de la homogénea anterior para las condiciones de contorno φ (0) = 0 , φ (L ) = φ 0 c) Obtener la solución general de la ecuación completa (1) para el caso de que Q ( x ) = e v≠ U L d) Obtener la solución general de la ecuación completa (1) para el caso de que Q ( x ) = e v= e) vx , con vx , con U K Si se considera la ecuación obtenida en a) como la de una familia de curvas de parámetro obtener su familia ortogonal φ0 , (1er Parcial 08) cálculo II etsiccpc problemas para practicar 3, EDOs de orden n curso 2009/10 1.- Los primeros puentes colgantes de cierta envergadura fueron construidos en Inglaterra y Francia a principios del siglo XIX. Todos ellos compartían una misma tipología, constituida por dos voluminosas torres de fábrica sobre los estribos, en las que se apoyaba una catenaria que sostenía una viga de celosía. El pionero en la construcción de los grandes puentes atirantados es John Augustus Roebling (18061869), de nacionalidad Alemana, estudió arquitectura en el Real Instituto Politécnico de Berlín, ciudad en la que además estudiaría filosofía, siendo discípulo de Hegel. En 1831 emigró a Estados Unidos donde materializaría toda su obra. La utilización de los recientemente desarrollados grandes cables de acero, capaces de soportar tensiones muy elevadas, marcarían todos sus proyectos. Algunas de sus primeras construcciones son el Acueducto de Delaware y el Puente de Monongahela. En 1855 proyecta el puente colgante sobre las cataratas del Niágara, con 250 metros de luz y dos pisos, uno inferior para el paso de tráfico rodado y uno superior para el paso de ferrocarriles. El puente estaba rigidizado con tirantes inclinados y celosías de madera. Su obra culminante y póstuma es el Puente de Brooklin, en Nueva York. Construido en 1883 sobre el East River, une la isla de Manhattan con el barrio de Brooklyn. Posee una luz de 486 metros y fue el puente colgante de mayor longitud nunca construido durante más de dos décadas. Apoyado sobre dos grandes torres de granito de estilo neogótico que sustentan la gran catenaria central, ha pasado a la historia como el primer gran puente atirantado. Puente de Brooklyn (1883) Se quiere obtener la ecuación, longitud y alargamiento de una de un cable sometido a una carga por unidad de longitud ρ g, suspendido de los puntos A(-a,0) y B(a,0) A(-a,0) y El equilibrio de fuerzas queda: T + ρg ds sen θ = (T + dT ) cos dθ (T + dT )sen dθ = ρg ds cos θ Donde T es la tensión sobre un punto del cable, horizontal, y s es la longitud del arco de catenaria. B(a,0) x Τ Τ+dΤ ds dθ θ ρgds θ es el ángulo que forma la recta tangente con la Con las simplificaciones sen dθ ≅ dθ , cos dθ ≅ 1 , dT dθ ≅ 0 , el sistema queda: ρg ds sen θ = dT ρg ds cos θ = T dθ (1) Se pide: a) Obtener de (1) la expresión que da la tensión en un punto del cable. (Solución T = b) Haciendo uso de (1) y (2) obtener la ecuación diferencial de la catenaria. T0 ) cos θ (2) (Solución: ρg 1 + y ′ = T0 y ′′ ) 2 c) Integrar la ecuación diferencial del apartado b) y obtener la solución particular que pasa por los puntos A(-a,0) y B(a,0). (Solución: y = T0 cosh ρg T ρg 0 ρg x − cosh a T 0 d) Calcular la longitud de la catenaria entre los puntos A y B. (Solución L = e) ρg 2T0 senh a ) ρg T 0 Si el alargamiento total del cable ( ∆s ) es la integral del alargamiento unitario ( ε ) por el diferencial de longitud (ds), esto es: B ∆s = ∫ ε ds , A y el alargamiento unitario del cable en un punto es la tensión que soporta el cable en ese punto, partido por el módulo de elasticidad y la sección del cable, siendo estas dos últimas constantes, esto es: ε= T , EΩ se pide calcular el alargamiento total del cable ( ∆s ). (Solución: ∆s = (Nota: T02 senh 2 ρg a + 2 ρg a T 2 EΩρg 0 T0 cosh 2 θ − senh 2 θ = 1 ; cosh 2 θ + senh 2 θ = cosh 2θ ) (Examen Final 1999) 2.- Sea la ecuación diferencial lineal, homogénea, de orden n y de coeficientes no constantes: y ( n + pn−1 (x ) y ( n−1 + pn−2 (x ) y ( n−2 +···+ p1 (x ) y′ + p0 (x ) y = 0 () (1) donde las funciones pi x , con i = 0,1,..,n-1, son continuas en un intervalo abierto que contiene la solución. En ciertos casos es posible resolver la ecuación (1) haciendo el cambio de variable dependiente (2) y = zϕ donde z es la nueva variable dependiente y ϕ es una solución particular de (1). A este procedimiento se le conoce como reducción de orden de una ecuación diferencial lineal homogénea. Se pide: a) Introducir el cambio de variable (2) en la ecuación diferencial (1) b) Introducir un segundo cambio de variable dependiente (z´= p) en la ecuación obtenida en a), de forma que se transforme ésta en una ecuación diferencial lineal, homogénea de coeficientes no constantes y orden n-1 c) Sabiendo que ϕ = x es una solución particular de la ecuación diferencial y′′ − 2x 2 y′ + 2 y=0 x −1 x −1 2 integrar la ecuación (3) haciendo uso del procedimiento anteriormente expuesto (3) (junio 2004) 3.- El puente colgante sobre el estrecho de Tacoma, en el estado de Washington, fue terminado en verano de 1940 y desde el primer momento estuvo sometido a oscilaciones verticales importantes del tablero, que por otra parte aparecen de forma relativamente frecuente en diversas tipologías de puentes. Sólo unos meses después de su finalización, el 7 de noviembre, y sometido a una velocidad de viento moderada de unos 70km/h, sufrió unas oscilaciones verticales de tal magnitud que acabaron haciéndose giratorias y terminaron con el colapso del mismo. El gobierno de EEUU encargó entonces un estudio al respecto a una comisión presidida por el ingeniero aeronáutico Theodore von Karman. A este investigador se debe el descubrimiento del fenómeno conocido como calle de von Karman , y que consiste en la aparición de una serie de remolinos de tamaño creciente que se emiten de manera periódica cuando un fluido rebasa un obstáculo a una velocidad considerable. Desde un primer momento se atribuyó la responsabilidad del colapso al fenómeno de resonancia que había tenido lugar en el mismo. La resonancia en este caso es el fenómeno lineal que se establecería por la coincidencia entre los movimientos periódicos del tablero y los provocados por el viento. Los efectos de la resonancia son la justificación que se ha dado tradicionalmente al colapso del Puente de Tacoma, por tanto la responsable última de la aparición de las grandes oscilaciones y la ruptura última del puente sería la aparición de oscilaciones crecientes provocadas por la coincidencia entre la frecuencia natural de las oscilaciones del puente y la de las fuerzas exteriores provocadas por el viento. Para ello sería necesario que hubiera una coincidencia total entre la frecuencia de la fuerza exterior y la natural del puente, además se deberían ignorar los efectos de amortiguamiento. Oscilaciones del puente de Tacoma (Washington), noviembre de 1940 Investigaciones posteriores realizadas por A. C. Lazer y P.J. McKenna, entre otros, y publicadas a finales del siglo pasado, han justificado el colapso del Puente de Tacoma como consecuencia de un fenómeno más complejo provocado en último caso por efectos no lineales de inestabilidad. Para ello desarrollaron una exposición analítica basada en la resolución de un problema diferencial en ecuaciones en derivadas parciales. Colapso del puente de Tacoma Se propone en este ejercicio evaluar de manera simplificada las vibraciones que pueden tener lugar en el tablero de un puente atirantado por el efecto de un viento de velocidad elevada. Para ello se propone un modelo muy simple constituido por una sección transversal del tablero que se supone sujeta a un solo cable de suspensión, que actúa a modo de muelle. La ecuación que regiría entonces el movimiento forzado no amortiguado sería: x′′ + ω 02 x = F (t ) donde x es el desplazamiento en altura, t es el tiempo, () ω0 (1) es la frecuencia natural de la oscilación del tablero y F t es la fuerza exterior producida por la acción del viento. Se pide resolver el problema según dos supuestos: a) En el primero se va a suponer que las vibraciones son efecto de la resonancia. En este caso se tomará ω 0 = 2 y la fuerza provocada por el viento se tomará como la suma de infinitas funciones senoidales de frecuencias crecientes y de amplitud αn conocida, esto es ∞ F (t ) = ∑α n sinnt . Se pide obtener la solución de (1) en estas condiciones. n =1 b) En un segundo supuesto se va a suponer que las vibraciones son consecuencia de un fenómeno más complejo de inestabilidad. Se considerará aquí que las oscilaciones responden a ciclos de subida y bajada del tablero de naturaleza distinta. En los de bajada, la constante del muelle (tracción del cable) se supone mayor que en los de subida (respuesta del cable a compresión, que se considerará muy pequeña pero no despreciable). Se supondrá por tanto un primer ciclo en el que se resolverá (1) con ω 0 = 2 y F t = sin 4t , junto con condiciones iniciales () x(0 ) = 0 , x′(0 ) = β y un segundo ciclo en el que se resolverá (1) con ω 0 = 1 , 2 π π F (t ) = sin 4t y condiciones iniciales x = 0 , x′ = − β + . 3 2 2 (junio 2005) 4.- Como sabemos, el cálculo diferencial es el lenguaje en el que se escriben los fenómenos de la naturaleza. Mediante las ecuaciones diferenciales (frente a las algebraicas) podemos expresar en términos matemáticos las leyes que gobiernan la física, para así poder prever el comportamiento del medio natural. La consideración de la variación de las magnitudes de manera diferencial nos permite describir los fenómenos de naturaleza ´suave’ y continua a lo largo del tiempo. Esta traducción al lenguaje del cálculo diferencial se realiza en gran parte de los casos imponiendo la conservación de la masa y de la cantidad de movimiento de los elementos diferenciales que componen el sistema. Como sabemos, el cálculo diferencial se fundamenta en los desarrollos obtenidos por Newton y Leibniz en la segunda mitad del XVII, que serían continuados por los Bernouilli, Euler y Lagrange, entre otros, durante el siglo siguiente. Leonhard Euler (1707-1783), para muchos el más grande matemático de todos los tiempos, denominará este método de aproximación a los problemas físicos método directo en oposición a un segundo método al que da el nombre de método de las causas finales. Según este segundo método las ecuaciones fundamentales que rigen los fenómenos de la naturaleza se obtienen no a través de establecer el equilibrio de magnitudes fundamentales sino mediante la obtención de los valores estacionarios de ciertas funciones. El método de las causas finales se basa por tanto en la rama de las matemáticas que, conocida como Cálculo de Variaciones, tiene en Euler a su figura fundamental. Al respecto de las dos formas de aproximación de los problemas de la física, Euler dice lo siguiente: ‘como la naturaleza del universo es la más perfecta, y es el trabajo del Creador más sabio, no hay nada que tenga lugar en el universo en lo que la relación de máximos y mínimos no aparezca. Por lo tanto no hay ninguna duda en absoluto de que cualquier efecto del universo puede ser explicado satisfactoriamente debido a causas finales, mediante la ayuda del método de los máximos y mínimos, como también puede serlo por las propias causas por las que tiene lugar[...]. Por lo tanto ante nosotros aparecen dos métodos de estudiar los efectos de la naturaleza; uno derivado de las causas actuantes, que se denomina habitualmente método directo, y el otro en términos de las causas finales[...]. Se debe hacer un especial esfuerzo para ver que ambas formas de aproximación a la solución del problema deben ser consideradas de manera conjunta; porque no sólo una solución es totalmente influida por la otra, sino que más aún, a partir del acuerdo entre las dos soluciones se asegura una resolución totalmente satisfactoria del problema planteado’ Una buena parte de los problemas físicos que se abordan durante las primeras etapas del desarrollo del cálculo diferencial tienen relación con el cálculo de estructuras. En este sentido, el problema de obtención de las deformadas de los elementos estructurales sometidos a esfuerzos es uno de los preferidos. El propio Leibniz (1646-1716) publica ciertas cuestiones al respecto de la obtención de las curvas elásticas en 1694 en su Acta Eroditorum Lipsia, pero sería Jacob Bernouilli (1654-1705) quien por primera vez tratará este problema de manera más rigurosa. El sobrino de éste, Daniel Bernouilli (1700-1782) y su discípulo Euler realizarán una contribución fundamental a la resistencia de materiales en general, y en particular a la obtención de las elásticas. En Methodus inveniendi lineas curvas, de 1744, Euler resuelve el problema de la forma que adquiere la deformadas de diversos elementos estructurales ante la acción de diferentes leyes de cargas haciendo uso del Cálculo de Variaciones (método de las causas finales). De esta forma obtiene la ecuación de la forma que adopta un cable pesado haciendo mínima la expresión integral que da la posición de su centro de gravedad ∫ L 0 yds , y que se obtiene también fácilmente mediante un equilibrio de fuerzas diferenciales (método directo). De manera análoga, Euler desarrolla en su Methodus inveniendi la obtención de la ecuación de la deformada de una viga sometida a una ley de flectores M(x), a partir de la consideración de los valores estacionarios de la ecuación integral ∫ L 0 ds , que da su energía potencial en términos del R2 radio de curvatura R. De esta forma obtiene que la ecuación de la deformada de una viga de módulo de elasticidad E y momento de inercia I , ambos constantes, sometida a una ley de flectores M(x) es: q EI = M (x ) R L x y (1) donde R es el radio de curvatura de una sección de la viga y viene dado por la expresión (1 + y′ ) R= 2 32 y′′ . Euler comprobó que efectivamente coincidía con la obtenida por Jacob Bernouilli por el método directo varios años antes, y que precisamente Euler determinó a petición de su maestro Daniel Bernouilli. Para el caso de la viga biapoyada de la figura, de longitud L, sometida a una ley de cargas q constante, y suponiendo despreciable y′ frente a y′′ , la ecuación (1) resulta: d 2 y q 2 qL EI 2 = x − x dx 2 2 (2) Se pide: a) Obtener la solución de la ecuación (2) para las condiciones de contorno de la viga del enunciado, esto es, y x = 0 = y x = L = 0 ( ) ( ) (1 + y′ ) C= 2 32 b) Obtener la solución de la ecuación diferencial de segundo orden y′′ , esto es, la familia de curvas cuyo radio de curvatura C es constante. ¿De qué curvas se trata? (1er parcial 2005) Nota: Se supone conocido que dx ∫ (1 + x ) 2 3/ 2 = x 1 + x2 +C 5.- La tipología más simple e intuitiva de un puente que salvara el paso a través de un pequeño río, podría consistir en una tabla de madera tendida entre sus orillas. La tabla va a flectar, esto es se ‘comba’, al paso de las cargas, pero no suele romperse por el peso de digamos una persona. Algún astuto hombre primitivo tuvo la feliz idea de remplazar esta tabla por una lámina de piedra, pongamos de pizarra, del mismo grosor y mucho más dura, pensó él, para así evitar la flexión y con ello el mojarse los pies en las crecidas del río. Para su sorpresa, se encuentra con que la tabla se rompe y él se moja de cuerpo entero al pasar por el puente. Nuestro astuto hombre de las cavernas no sospecha que la pizarra no tiene apenas resistencia a tracción, tampoco sabe que el momento flector al que se ve sometida la sección de centro luz del puente de piedra en las fibras (cara) inferiores provoca unas tracciones que suponen el colapso de su puente de piedra. Ley de momentos flectores de la ‘Tabla’ para carga uniforme. Sección central del puente Otra posible tipología que nuestro hombre de las cavernas podría utilizar basándose en la intuición para conseguir cruzar seco, sería la sustitución de la ‘tabla de piedra’ por un arco del mismo material, que a modo de ‘cáscara de huevo’ de dos dimensiones, aguante el peso sin romperse. En realidad lo que estaríamos haciendo es reducir a un mínimo el momento flector, que es sustituido en este caso por un esfuerzo a compresión en el que la piedra demuestra sus mejores cualidades. De ahí que sea muy rara la tipología de grandes puentes viga (‘tabla’) de piedra, frente a la tan repetida forma en arco. Habríamos inventado el puente de dovelas de piedra. La geometría ideal para un puente en el que quisiéramos eliminar por completo las tracciones sería la correspondiente a un cable no rígido sometido a unas cargas de igual magnitud pero sentido contrario, al que pondríamos ‘cabeza abajo’. Una vez hemos dado la vuelta a esa estructura, la gravedad cambia de sentido con respecto a ella y los esfuerzos de tracción con los que trabajaba el cable de forma exclusiva, pasan a ser de compresión, que son los que nos interesan. Si las cargas que van a actuar sobre un puente fueran de peso propio, la forma del arco sería la de una catenaria invertida como ya sabemos. Sin embargo es más realista considerar el peso propio del puente despreciable con respecto a las cargas de uso, que podemos suponer constantes a lo largo de la horizontal. El heredero estructural de la piedra en la arquitectura de hoy es el hormigón que, siendo mucho más cómodo de utilizar que la piedra por su sencillo proceso constructivo, sigue sin tener resistencia a tracción. Por ello, el puente arco de hormigón es uno de los más comúnmente utilizados. Para luces pequeñas suele coexistir con el de vigas (tabla) que se hace resistente a tracción mediante la adición de barras de acero en las fibras traccionadas. El puente arco de hormigón, consigue así salvar grandes luces, con limpieza de formas y economía en el armado. Puente arco de ferrocarril de Plfaffenberg (Tauern. Austria) de 200 m de luz. Se pide: a) Obtener el equilibrio de fuerzas en la dirección tangente y normal, de un cable de peso despreciable sometido a una carga uniforme de p (N/m) a lo largo de la horizontal, suponiendo que para ángulos pequeños sen dθ ≅ dθ , cos dθ ≅ 1 , y dT ⋅ dθ ≅ 0 . Τ+dΤ Τ ds dθ θ p (N/m) b) A partir del sistema anterior, obtener la ecuación diferencial de orden dos de la forma que adopta el cable e integrarla. ¿Qué familia de curvas se obtiene? c) Dando la vuelta a la solución obtenida en b) obtener la ecuación analítica del puente arco que pasa por los puntos (-a, 0) y (a, 0). d) Obtener las ecuaciones paramétricas de la familia de ortogonales e isogonales a 45º al haz curvas de parámetro a obtenida en c). (Febrero 2000) 6.- Dada la ecuación diferencial y′′ + P(x ) y′ + Q(x ) y = R(x ) a) er Obtener la condición (una ecuación diferencial (2) de 1 orden de variable dependiente (1) s (x ) ) para que u = y′ + sy , transforme (1) en una ecuación diferencial (3) lineal de 1er orden en la variable dependiente u ( x ) el cambio de variable b) ¿De qué tipo de ecuación diferencial de 1er orden se trata la ecuación (2) obtenida en el apartado anterior? c) Si d) Suponiendo conocida e) Sabiendo que s p = s p (x ) es una solución particular de (2) ¿Cuál es la solución general de (2)? s p , integrar la ecuación (1) haciendo uso del cambio de variable u = y′ + s p y sp = x es una solución particular de iniciales y (0 ) = y′(0 ) = 1 2 y′′ + xy′ + y = − xe − x 2 mediante el cambio de variable u = y′ + xy 7.- Sabiendo que s′ = 1 − sx + s 2 , resolver el problema de valores 2 y = x − 1 es solución de 1 + x 2 y′′ − 2 xy′ + 2 y = 0 ( (febrero 06) ) obtener su solución general por reducción de orden Se recuerda que el procedimiento de reducción de orden para integración de una ecuación diferencial de la forma (1) y ( n + pn−1 (x ) y ( n−1 + pn−2 (x ) y ( n−2 +···+ p1 (x ) y′ + p0 (x ) y = 0 consiste en introducir el cambio de variable y = zϕ , donde z es la nueva variable dependiente y ϕ es una solución particular de (1) 8. Integrar la ecuación (junio 06) (2 x + 1)y′′ + (4 x − 2)y′ − 8 y = 0 sabiendo que admite una solución de la forma y = e mx , con m ∈ R (junio 06) Why should I refuse a good dinner simply because I don't understand the digestive processes involved? Oliver Heaviside (1850-1925) 9.Oliver Heaviside (1850-1925), físico y matemático fundamentalmente autodidacta, es el autor de importantes descubrimientos en el campo del electromagnetismo, la propagación de ondas y el cálculo diferencial. Nació en Londres en el seno de una familia de artesanos y desde pequeño sufrió de una salud delicada, lo que le provocó entre otras cosas una sordera progresiva desde temprana edad que marcó su carácter introvertido y psicológicamente inestable. Desde pequeño destacó como alumno aventajado, sin embargo abandonó los estudios con 16 años para prepararse como empleado de telégrafos, labor que desempeñaría durante largo tiempo primero en Dinamarca y luego en Newcastle, en la Great Northern Telegraph Company. Sus primeros y más prolongados trabajos de investigación fueron dedicados a la electricidad y el magnetismo, campo en el que obtendría importantes logros científicos como queda reflejado en diversos trabajos por él publicados a partir de 1872, así como en referencias de James Maxwell, con quien colaboró en diversos temas de electromagnetismo, teoría de ondas y telegrafía, y con quien formularía las conocidas ecuaciones de Maxwell (también junto a Gibbs). De entre sus desarrollos en el campo de la física cabe destacar como más importantes el desarrollo de la teoría del circuito sin distorsión, que sería continuado por Michael Pupin para el desarrollo de la telefonía a larga distancia, y el descubrimiento de la capa atmosférica ionizada que permite la propagación de las ondas radiofónicas. Además de los importantes desarrollos obtenidos en el campo del electromagnetismo, Heaviside ha pasado también a la historia de la ciencia por sus contribuciones en el campo del cálculo diferencial. Heaviside desarrolló entre 1880 y 1887 la teoría de los operadores diferenciales que llevan su nombre como herramienta para resolver las ecuaciones diferenciales ordinarias que se obtienen en la teoría de circuitos eléctricos. Como sabemos, dicha teoría está basada en sustituir el operador diferencial d dx por el operador algebraico D, transformando de esta forma las ecuaciones diferenciales en ecuaciones algebraicas que una vez resueltas se volvían a transformar en soluciones de la ecuación diferencial de partida. En el campo de las matemáticas obtuvo también importantes desarrollos en teoría de números complejos (para poder aplicarla sobre la teoría de los circuitos eléctricos), el método de la transformada de la Laplace para la resolución de ecuaciones diferenciales (para ello utilizaría la función escalón que lleva su nombre), y el análisis vectorial (también para utilizarlo en sus desarrollos sobre electromagnetismo). Como tantos otros matemáticos destacados de la historia consideró siempre las matemáticas como una herramienta para lograr sus objetivos en el campo de la física y en concreto del electromagnetismo, y no fue demasiado ortodoxo es sus desarrollos matemáticos. A pesar de la innegable utilidad de los métodos diferenciales de Heaviside, que fue presentada en numerosos artículos de Proceedings of the Royal Society ante la comunidad científica mundial, la falta de rigor en su exposición, hizo que algunos de los más grandes matemáticos de la época objetaran con vehemencia lo adecuado de dichos métodos. Entre estas posiciones críticas cabe destacar las de Tait y Burnside además de la de Gibbs. Habrá que esperar a los trabajos de Bromwich para contar con demostraciones matemáticas de rigor al respecto. De personalidad atormentada, como la de tantos otros grandes científicos, parece ser que durante los últimos años de su vida padeció diversas patologías psiquiátricas como manía persecutoria y síndrome de diógenes entre otras. A pesar de recibir ciertos honores en vida, como su ingreso en la Royal Society en 1891, murió solo y sin que su labor científica fuera reconocida como merecía. Se pretende resolver un problema diferencial sencillo de electricidad haciendo uso de los métodos desarrollados por Heaviside entre 1880 y 1887. Un circuito RLC está constituido por una batería que suministra una diferencia de potencial de V(t) Voltios, una resistencia de R Ohmios, una inductancia de L Henrios y un condensador de capacidad C Faradios, todos ellos colocados en serie (ver figura). La ecuación diferencial que gobierna la carga en culombios q(t) del circuito para un instante de tiempo t, es la siguiente: d 2q dq 1 L 2 +R + q = V (t ) dt C dt Se pide: a) Si V(t)=ex Voltios, R=4 Ohmios, L=1 Henrio y C que da la carga q(t) del circuito en un instante de operacionales de Heaviside b) Si V(t)=ex Voltios, R=2 Ohmios, L=1 Henrio y C que da la carga q(t) del circuito en un instante de operacionales de Heaviside R 1/C L V =1/3 Faradios, obtener la solución general tiempo dado, haciendo uso de los métodos =1/2 Faradios, obtener la solución general tiempo dado, haciendo uso de los métodos (febrero 06) 10. En la teoría de elasticidad de los suelos se conoce como terreno winkler a un modelo que aproxima la interacción entre una estructura de cimentación y el terreno a un número infinito de muelles de módulo de elasticidad k (o módulo de reacción vertical o coeficiente de balasto) de forma que la fuerza de restitución del terreno sobre el cimiento sea –ky, donde y es la deformación que tiene lugar sobre la estructura. q(x) x y El nombre de balasto proviene del análisis de las traviesas de ferrocarril, donde se utilizó por primera vez este modelo. El terreno winkler tiene múltiples aplicaciones en el cálculo de estructuras, de las cuales la más importante es el cálculo de cimentaciones, y en particular el cálculo de vigas flotantes o de cimentación y losas de cimentación que trabajan sobre una sección horizontal del terreno. También es aplicable a elementos tales como pantallas para excavaciones o tablestacas que trabajan sobre una sección vertical. Se habla por tanto en esos casos de módulo de balasto vertical y de módulo de balasto horizontal. Se desea calcular una viga de cimentación que se asienta sobre un terreno con constante de balasto k. La ecuación diferencial de la deformada de la viga sometida a una carga q(x) es EI d4y + ky = q(x ) dx 4 donde E e I son el módulo de elasticidad y el momento de inercia de la sección de la viga, ambos constantes. La deformada se puede de esta forma evaluar a través de la ecuación diferencial lineal completa de cuarto orden y coeficientes constantes y iv + k q(x ) y= EI EI Si se asume que q(x) es uniforme a lo largo de toda la longitud de la viga e igual a q y que k / EI ≈ 4 , se pide obtener la deformada de la viga en estas condiciones para las condiciones de contorno de viga biapoyada en los extremos. Suponiendo que la longitud de la viga es π , las c.c. serán por tanto y (0 ) = y (π ) = y′′(0 ) = y′′(π ) = 0 Nota: Se recuerda que las raíces de la ecuación x 4 + 4 = 0 son 1 ± i y −1 ± i (junio 07)