tema5
Anuncio

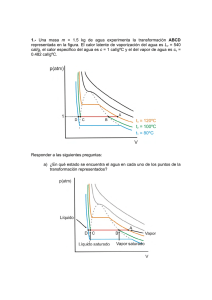
PROBLEMAS tema 5 5.1. Supóngase que dos subsistemas A y B están separados por una pared diatérmana, rígida e impermeable. El subsistema A tiene un volumen de 9 ml y un número de moles igual a 3. El subsistema B consta de 2 moles y tiene un volumen de 4 ml. La energía interna total del sistema es 20 cal y el sistema global A+B se considera aislado. Representar la entropía total S en función de la fracción UA/(UA+UB). Cuando el sistema ha alcanzado el equilibrio, ¿cuáles son las energías internas de cada uno de los subsistemas A y B?. Datos.- SA=cte.(nAVAUA)(1/3) SB=cte.(nBVBUB)(1/3) ( ) Solución.- S = cte 201/3 3x1 / 3 + 2(1 − x )1 / 3 ; siendo x=UA/(UA+UB). En el equilibrio (dS=0) UA=12.96 y UB=7.04. 5.2. Determinar ∆U y ∆H de 3 Kg de aire cuando pasan de 8 Kg/cm2 y 15 ºC a la misma presión y 600 ºC. Para el aire CP = 0.231 + 0.35 104T cal/g.grado. Nota. Suponer que el aire es un gas ideal y tomar 28.9 g/mol como su peso molecular. Solución.- ∆H=441062 cal, ∆U=320398 cal. 5.3. Las propiedades termodinámicas del vapor de agua obtenidas en las tablas son, para la P y T indicadas, las siguientes: Estado P(atm) t(ºC) h(Kcal/Kg) s(Kcal/Kg.K) v(m3/Kg) 1) 12 680 926 1.95 0.372 2) 1 680 927 2.22 0.448 Determinar el Wmax que se pone en juego cuando 5 moles de vapor pasan del primero al segundo de los estados arriba indicados. (1 atm.litro = 24.22 calorías). Solución.- 14.31 Kcal. 5.4 Se estira reversiblemente una lámina de agua a Py T constantes hasta que su superficie aumente en 1 cm2. El cambio de energía libre para dicho aumento de superficie viene dado por la expresión: G2-G1=75.64 - 0.14 t (t en ºC y G2-G1 en érgios) El volumen total del agua puede suponerse constante. Se pide: a) W puesto en juego en el estiramiento de la lámina a la temperatura de 10 ºC. b) Calor absorbido durante el proceso de estiramiento. c) Incrementos de U, H, S y F para el alargamiento. d) Después de estirada, se deja que la lámina recobre espontánea e irreversiblemente su área inicial. No se recupera trabajo en este proceso. ¿Cuánto vale ∆G para la contracción espontánea?. e) Calcular Q, ∆U, ∆H, ∆S y ∆F para el proceso de contracción espontánea. Solución.- a) –74.24 érgios, b) Q=39.62 érgios, c) ∆U=113.86 érgios, ∆H=113.86 érgios, ∆S=0.14 érgios/K, ∆F=74.24 érgios, d) ∆G=-74.24 érgios, e) Q=-113,86 érgios, ∆U=-113.86 érgios, ∆H=-113.86 érgios, ∆S=-0.14 érgios/K, ∆F=-74.24 érgios. 5.5 La transición entre el azufre rómbico y el monoclínico se produce de forma reversible a la temperatura constante de 95.5 ºC y presión de 1 atm. Las entropías molares absolutas de las dos formas halotrópicas están dadas por: S(rómb) = -14.61+ 3.58 lnT+ 0.00624 T cal/mol K S(monoc) = -14.55+ 3.56 lnT+ 0.00696 T cal/mol K Calcular el incremento del potencial molar de Gibbs para el proceso: , 1atm S(rómb) 298 K → S(monoc) Solución.- ∆G=12.96 cal. 5.6 Un mol de acetona se calienta desde una temperatura de 293 K hasta alcanzar el equilibrio con el ambiente a 343 K (en una estufa isoterma), a la presión normal de una atmósfera. Se pide: a) La variación de entropía del sistema (acetona), del ambiente (estufa) y del universo. b) La variación de las demás funciones termodinámicas (U, H, G y F) de la acetona. Datos Para la acetona: Teb = 329.12 K, Calor latente de vaporización (Lv) =124.5 cal/g, CP(líq)=0.32 cal/g K, CP(vap) = 0.15+0.0023 T cal/g K, S(a 293 K) = 45.6 cal/mol K. Nota.- Admitir comportamiento ideal para el vapor y suponer el líquido incompresible. Ayuda.- Para calcular el ∆S de la acetona considera el proceso en varias etapas: acet.(liq,297K) → acet.(liq,329.12K) → acet.(vap,329.12K) → acet.(vap,343K). El calor involucrado en la segunda etapa es el calor de cambio de fase a temperatura cte 329.12K. En el apartado b), para calcular el ∆U, debe calcularse el Q y el W. A P=cte el W=P(V2-V1) ≅ PV2=RT2. Solución.- a) ∆Sacet.=26.31 cal/K, ∆Sestufa =-25.17 cal/K, ∆Su=1.14 cal/K. b) ∆U=7952 cal, ∆H=8634 cal, ∆G=-2669.5 cal, ∆F=-3351.1 cal. 5.7 La tabla adjunta nos da, a 25 ºC y P=1 atm, las entalpías molares, las entropías molares y las densidades de dos variedades cristalinas del carbono: el diamante y el grafito. h (Kcal/mol) s (Kcal/mol ρ (Kg/m3) K) C(diamante) 172.15 0.6 10-6 3.51 103 -3 C(grafito) 171.70 1.36 10 2.26 103 a) ¿Cuál es la forma estable a 25 ºC y 1 atm de presión b) ¿Bajo qué presión, siempre a 25 ºC, se convierte en estable la otra forma Nota.- Suponer las densidades independientes de la presión. Ayuda.- Los datos permiten calcular el ∆g para el proceso C(diamante) → C(grafito). Si a 25 ºC y 1 atm resulta ∆g<0, entonces el grafito es la forma termodinámicamente estable. En el apartado b), de la expresión dg=-sdT+vdP, a T=cte, resulta dg=vdP. De ella es inmediato obtener d∆g=∆vdP (∆g=ggraf-gdiam y ∆v=vgraf-vdiam). Como nos dicen que las densidades pueden suponerse constantes, ∆v será constante y la integración de d∆g=∆vdP desde P=1 hasta P (presión a la cual comienza a ser estable la otra forma halotrópica) nos dará el valor de la P límite. Solución. a) Para C(diamante) → C(grafito), ∆g (298K,1atm)=-0.854 Kcal/mol<0 ⇒ grafito es más estable. b) Para P=18647 atms (a 298K) comienza a ser estable el diamante. 5.8. La ecuación térmica de estado de un mol de cierto gas real viene dada por (P + a / v 2 ) (v - b) = RT , donde a y b son constantes. La capacidad térmica molar a volumen constante varía con la temperatura según CV = α + βT. Calcular las variaciones de energía interna U2−U1 y de entropía S2−S1 cuando 1 mol de dicho gas pasa del estado 1 (P1, v1, T1) al estado 2 (P2, v2, T2). Solución. ∆U = α (T2 − T1 ) + (β / 2) (T22 − T12 ) + a (1/v1 − 1 / v 2 ) v −b ∆S = α ln(T2 / T1 ) + β (T2 − T1 ) + R ln 2 v1 − b Ayuda. El paso del estado 1 al estado 2 puede hacerse tal como se indica en la figura P P2 2 A T2 P1 1 T1 V v2 v1 La integración de 1 a 2 puede hacerse mediante los procesos reversibles siguientes: de 1 a A (isócoro) y de A a 2 (isotermo).