Paralaje estereoscópica
Anuncio
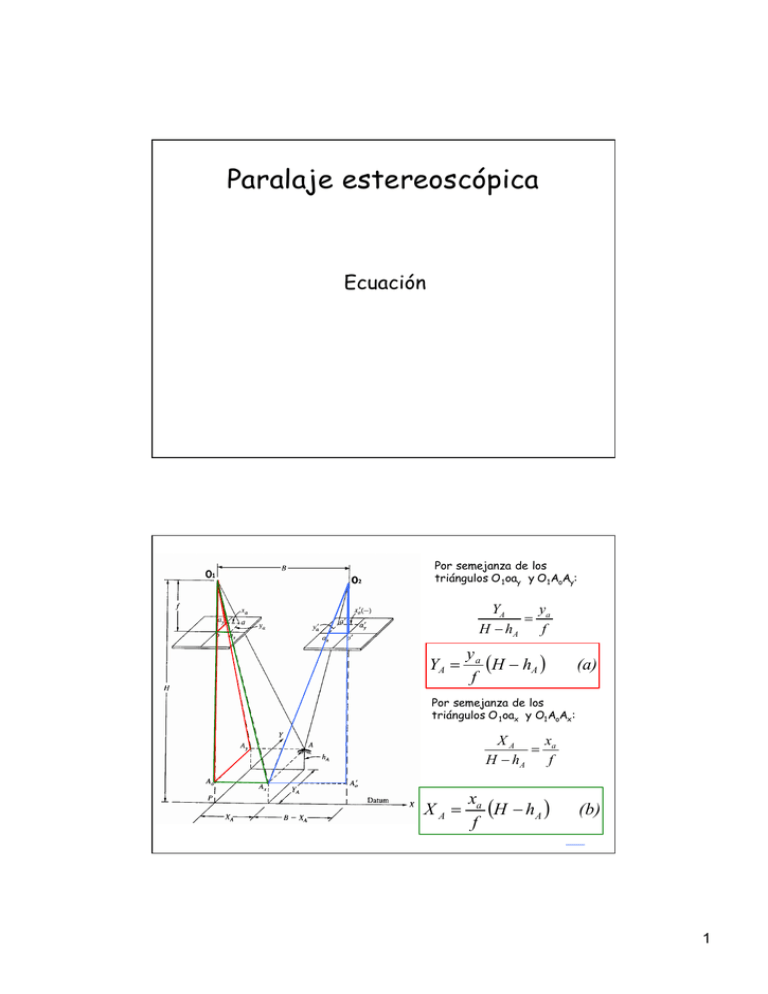
Paralaje estereoscópica Ecuación Por semejanza de los triángulos O 1 oay y O 1 AoAy: YA y = a H − hA f YA = ya (H − hA ) f (a) Por semejanza de los triángulos O 1 oax y O1 AoAx: XA x = a H − hA f XA = xa (H − hA ) f (b) 1 También por semejanza de los triángulos O2o’a’x y O2A’ oAx: B − X A − xa' = H − hA f xa' X A = B + ( H − hA ) f ; (c) Igualando las ecuaciones (b) y (c) y simplificando tenemos: hA = H − Bf xa − xa' (d) Sustituyendo pa por xa –x’ a en la ecuación (d) se tiene: Bf pa hA = H − ( 1− 1) Sustituyendo la ecuación (1-1) en las ecuaciones (a) y (b) y operando: XA = B xa pa ( 1− 2 ) YA = B ya pa (1− 3 ) Cálculo de altitudes por diferencias de paralajes O1 Con la fórmula obtenida se pueden calcular altitudes O2 B h=H − f a1 c2 a2 Bf p pero es más conveniente emplear diferencias de paralaje c1 pA = Bf H − hA pC = Bf H − hC H A ∆pAC = hA C Datum haciendo operaciones se llega a: de donde: hC y hA = hC + Bf(hA - hC ) (H - hA )(H - hC ) hA − hC = ∆pAC pA (H - hC ) ∆pAC (H -hC ) pA 2 Ecuación aproximada para el cálculo de altitudes hA = hC + O1 ω1 ∆AC (H - hC ) pA O2 a1 ω’1 ω’2 ω2 b a2 Para un terreno de relieve no muy acusado se puede sustituir hc por hm, altitud media y H será Hm, también podrá sustituirse pA por b (base medida en la fotografía) En terreno llano, al estar todos los puntos a igual distancia, sus paralajes son todos iguales. En particular, lo serán al del punto principal Ω 1. pω 1 = 0 –(-b) = b Ω1 A Ω2 Y todos los puntos Si el relieve no es muy fuerte p ˜ b obteniendo: pΑ= b hA − hC = pAC Hm b Gráficos de corrección de paralajes Debidos a una serie de causas de error: 1) Las fotos no han sido tomadas rigurosamente en “caso normal” 2) No se han colocado correctamente para la medida 3) El soporte no es enteramente estable y 4) Hay un conjunto de distorsiones se pueden corregir las paralajes medidas, por medio de gráficos, si se disponen de puntos de control de altitud conocida pA = Bf H − hA pC = Bf H − hC ∆pAC = (hA - hC ) p (H - hA ) C Y para un punto cualquiera con origen en el punto C ∆p = (h - hC ) p (H - h ) C Conocido un valor de H podrán calcularse las diferencias de paralaje y por tanto las correcciones a las medidas y trazar las isolineas correspondientes. 3 Errores en la medida paraláctica de altitudes Partiendo de la fórmula: hA = H − Bf pa Y asumiendo que no existen errores en las medidas de H, B y f y que la única causa de error procede de la medida de la paralaje, diferenciando respecto a p se obtiene: Bf dh = Pero como p= p2 dp Bf H −h Sustituyendo queda si consideramos h << H H2 dh = dp Bf Problema de paralaje 1) Se han tomado un par de fotografías aéreas con una cámara de focal 152,4 mm desde una altura de vuelo de 1233 m. La base aérea fue de 390 m. Las coordenadas de dos puntos a y b, en mm, respecto a la línea de vuelo fueron: Foto Izq. Foto Dch. x y x y a 53,41 50,84 -38,26 50,86 b 88,92 -46,69 -7,06 -46,69 Calcular las altitudes de A y B y la distancia horizontal AB. 4 Problemas de paralaje (cont.) 2) Partiendo de los datos del problema anterior, se tienen además las coordenadas de un punto C de control vertical que son: x = 14, 3 mm y x’=-78,3 mm. Si la altitud de dicho punto es de 591 m. calcular las altitudes de los puntos A y B utilizando las diferencias de paralaje. 3) Se han tomado un par de fotografías aéreas con un recubrimiento del 60% longitudinal y con una cámara de focal 152,4 mm y una base de 548 m. La altitud del punto de control A es de 283 m y la paralaje de 92,4 mm. ¿Cuál es la altura de vuelo de las fotografías? Problemas de paralaje (cont.) 4) La distancia horizontal AB es de 650,47 m, las fotocoordenadas medidas respecto al eje de vuelo son: Foto Izq. Foto Dch. x y x y a 33,29 13,46 -52,32 13,46 b 41,76 -95,76 -44,96 -95,76 Calcular la base aérea 5) Se ha tomado un par de fotografías aéreas con un recubrimiento del 60% longitudinal y con una cámara de focal 152,4 mm desde una altura de vuelo de 1622 m. La altitud del punto de control C es de 263 m y la paralaje de 86,3 mm. ¿Cuál es la base aérea de las fotografías? 5 Problemas de paralaje (cont.) 6. Se han tomado un par de fotos aéreas desde una altura de vuelo de 1082 m sobre el terreno con una cámara de focal 152,46 mm. Las coordenadas x en la foto izquierda de la base y de la copa de un árbol son 81,53 mm y 84,33 mm respectivamente. En la foto derecha son -12,45 mm y -14,22 mm. Determinar la altura del árbol. 7. La base aérea de un par de fotos aéreas verticales es de 757 m . La focal de la cámara es de 152,35 mm . Las coordenadas imagen de un punto A, cuya altitud es de 282 m fueron en la foto izquierda de x = 3,29 mm y en la derecha de -84,98 mm ¿Cuál es la altura de vuelo sobre el datum? Problemas de paralaje (cont.) 8. Se han tomado un par de fotos aéreas desde una altura de vuelo de 1835 m sobre la base de una antena de radio . Las coordenadas x en la foto izquierda de la cima y la base de la antena son 96,52 mm y 90,49 mm respectivamente. En la foto derecha son -1,05 mm y -0,98 mm respectivamente ¿ Cuál es la altura aproximada de la antena? 9. Los errores accidentales en la medida de la altitud de un punto A por medio de la barra de paralajes han sido ±1,5 m en H, ±1,5 m en B y ±0,03 m en pa . Sabiendo que p A = 91,67 mm calcular el error resultante en hA debido a cada una de las fuentes de error así como el efecto total debido a los tres errores. 6 Problemas de paralaje (cont.) 10. Se han tomado un par de fotos verticales con una cámara de focal 152 mm desde una altura de vuelo sobre el nivel del mar de 2100 m. La base aérea es de 988 m. El par estereoscópico se orientó para me dir respecto a la barra de paralajes cuya constante es C = 67,45 mm. Calcular las lecturas de paralaje necesarias para trazar las curvas de nivel de 225, 250, 275 y 300 metros. 11. Se han obtenido un par de fotogramas verticales con recubrimiento desde una altitud de 1334 m. Las altitudes y lecturas de la barra de paralajes de 5 puntos de control son las que aparecen en el cuadro. Construir un gráfico de corrección de paralaje, usar el punto E como referencia. La constante de la barra es C= 74,55 mm. Las fotocoordenadas de los 5 puntos pertenecen a la foto izquierda. Puntos Altitud (m) r (mm) x (mm) A 425,20 28,63 12,3 y (mm) 94,1 B 429,77 29,11 98,2 90,3 C 359,05 21,56 80,1 11,6 D 381,91 23,82 -6,2 -90,8 E 317,60 17,55 89,9 -87,4 7









