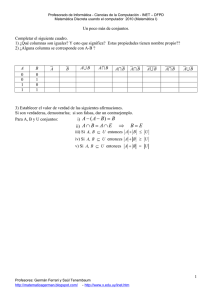
Teoría Unidad 1 - Facultad de Ingeniería
Anuncio

UNSa- Facultad de Ingeniería
CIU 2011
ÁREA MATEMÁTICA
Unidad 1: Conjuntos numéricos
UNIDAD 1: CONJUNTOS NUMÉRICOS
1.1 NOCIONES BÁSICAS DE CONJUNTOS
Los términos elemento, conjunto y pertenencia pueden tomarse como conceptos primitivos,
vale decir, que se aceptan sin definir. No obstante, es bastante clara la noción de que una
agrupación de entidades cualesquiera (elementos) constituye un conjunto, y que pertenencia es la
vinculación entre elemento y conjunto.
Así, podemos hablar de entidades concretas- conjunto de juguetes, conjunto de alumnos de
un colegio-, o más abstractas, como símbolos. En particular, nos interesarán los conjuntos de
números.
Un conjunto puede definirse por extensión o enumeración, es decir, mencionando los
elementos que lo componen, o bien por comprensión, designando una propiedad común a todos
ellos y que los precisa.
Por ejemplo:
A = {Pedro, Juan, Lucio}
A = {alumnos var ones de 5º grado del colegio NN }
Denominamos conjunto referencial o universal, o universo, a aquél formado por todos los
elementos del tema de referencia; por ejemplo:
U = {alumnos del colegio NN }
sido
El universo puede variar, según de qué contexto se hable, por ejemplo, también podría haber
U = {alumnos de 5º de los colegios de Salta}
B = { 3, 4, 5, 6,….}
En el caso del conjunto B los puntos suspensivos se utilizan para indicar que el conjunto sigue
indefinidamente; es un conjunto infinito.
Notaciones:
La notación “a∈A” significa que a es un elemento del conjunto A y se lee: “a pertenece a A”Ej.
martes ∈A
La notación “a ∉ A” significa que a no es un elemento del conjunto A y se lee: “a no pertenece a
A” lunes ∉ A
Dos conjuntos son iguales cuando tienen los mismos elementos
“A⊂B” se lee A esta incluido o contenido en B” y significa que todo elemento de A es también
elemento de B
La notación para el conjunto vacío es φ o {}
Operaciones con conjuntos:
Dados dos conjuntos A y B, recordaremos algunas operaciones elementales entre ellos que tiene
como resultado otro conjunto.
Unión: El conjunto A∪B (se lee “A unión B”) es el conjunto formado por todos los elementos
comunes y no comunes de A y de B.
A ∪ B = {x / x ∈ A ∨ x ∈ B}
CM. Borré
Pág. 1
UNSa- Facultad de Ingeniería
CIU 2011
ÁREA MATEMÁTICA
Unidad 1: Conjuntos numéricos
A
U
B
Intersección: El conjunto A∩B (se lee “A intersección B”) es el conjunto formado por todos los
elementos comunes a ambos conjuntos.
A
U
A ∩ B = {x / x ∈ A ∧ x ∈ B}
B
Es claro que, vista la definición de intersección, podemos especificar en la unión de conjuntos:
A ∪ B = {x / x ∈ A ∨ x ∈ B ∨ x ∈ ( A ∩ B)}
Diferencia: A-B (se lee A menos B) es el conjunto formados por todos los elementos que
pertenecen a A pero que no pertenecen a B
A − B = {x / x ∈ A ∧ x ∉ B}
A
U
B
Complemento: Definido un conjunto universal o de referencia, que llamaremos R o U, y dado un
conjunto A, se llama complemento de A y se denota Ac al conjunto formado por todos los
elementos de U que no pertenecen a A.
Ac=U-A= {x / x ∈ U ∧ x ∉ A}
A
U
1.2 CONJUNTOS NUMÉRICOS:
Los elementos que pertenecen a un conjunto pueden ser de cualquier naturaleza. En particular,
nosotros estamos interesados en aquellos cuyos elementos son números. Por este motivo,
repasaremos algunos conceptos relacionados con estos conjuntos, las operaciones entre números y
sus propiedades.
1.2.1 Conjunto de Números Naturales:
Probablemente, haya sido la necesidad de contar la que haya desarrollado la primera Matemática.
Los números que utilizamos para contar: 1, 2, 3, … conforman el conjunto de los números
naturales. A este conjunto se lo indica con la letra N, o N0 en el caso de considerar al cero como un
elemento perteneciente a él.
Los elementos están ordenados en un conjunto que tiene un primer elemento que es el 1, cada
elemento salvo el 1 en N o el 0 en N0 tiene su antecesor (anterior) y su sucesor (posterior). Se
pueden representar en una recta numérica.
CM. Borré
Pág. 2
UNSa- Facultad de Ingeniería
CIU 2011
ÁREA MATEMÁTICA
Unidad 1: Conjuntos numéricos
En este conjunto siempre podemos realizar sin problemas las operaciones de suma y
producto, obteniendo otro número natural como resultado (operaciones cerradas en N).La
diferencia cuando el sustraendo es mayor que el minuendo, no tiene solución en el conjunto N; por
ejemplo:
(5 - 8 ) ∉ N .Necesitamos incorporar los números negativos.
Los puntos denotan los números naturales. Decimos que N es un conjunto discreto.
Así, N ⊂ N 0
1.2.2 Conjunto de Números Enteros:
Si además de los números naturales consideramos los números negativos -1, -2, -3,… y el 0
formamos el conjunto de los números enteros, que denotamos con la letra Z.
Los elementos están ordenados en un conjunto que no tiene ni principio ni fin y cada elemento tiene
su antecesor (anterior) y su sucesor (posterior). Se pueden representar en una recta numérica:
En este conjunto la suma, la resta y el producto siempre resultan enteros, pero en la división, si el
dividendo no es múltiplo del divisor, no obtenemos un número entero.
(13/2) ∉ Z .Necesitamos, entonces incorporar a las fracciones y formaremos un nuevo conjunto
numérico que será el de los racionales(Q). También vemos que Z es un conjunto discreto.
Así, N ⊂ N 0 ⊂ Z
1.2.3 Conjunto de Números Racionales:
La palabra racional viene de razón, pues los números racionales son aquellos que se pueden
expresar como una razón (o relación, o cociente), entre dos enteros, a excepción del cero en el
denominador.
Si a y b son enteros, siendo b ≠ 0 ,entonces, la razón:
r = a/b, es un número racional
1
1 − 3 2 22 13 2
Por ejemplo, son números racionales, los números: ;
; ; ; ;
;−
2 5 4 3 6 −3 3
Observemos que, para los racionales negativos, es indistinto que el signo menos afecte al
numerador, al denominador, o que antepongamos el signo “-“, afectando a toda la fracción: las
expresiones son equivalentes, es decir, representan un mismo número.
El conjunto de los números racionales se representa con la letra Q.
En la recta numérica están representados algunos números racionales:
CM. Borré
Pág. 3
UNSa- Facultad de Ingeniería
CIU 2011
ÁREA MATEMÁTICA
Unidad 1: Conjuntos numéricos
A diferencia de los anteriores, Q no es un conjunto discreto, sino denso, vale decir, que entre dos
racionales hay siempre hay otro racional; de este modo, existen pues infinitos números racionales
comprendidos entre dos dados.
Estos números también tienen una representación decimal que se obtiene dividiendo el numerador
por el denominador:
1
= 0,25
4
−3
= −0,6
5
2
= 0,25
8
CM. Borré
(decimal exacto)
(decimal exacto)
(decimal exacto)
)
22
= 7,3333... = 7,3 (decimal
3
periódico puro)
)
13
= 2,1666... = 2.16 (decimal
6
periódico mixto)
Pág. 4
UNSa- Facultad de Ingeniería
CIU 2011
ÁREA MATEMÁTICA
Unidad 1: Conjuntos numéricos
Observamos que 1/4 y 2/8 representan el mismo número, o sea hay infinitas formas de
representación en forma de fracción de un número racional; algunos autores consideran que siendo
primos entre sí numerador y denominador, y éste distinto de 1- la fracción es irreductible -y el
2 6
número es un número fraccionario puro. No olvidemos que = y representan el entero 2, que
1 3
también pertenece a Z.
Así, N ⊂ N 0 ⊂ Z ⊂ Q
En algunas divisiones el resto de la misma es cero, y la expresión será decimal exacta; en caso
contrario, la expresión será periódica: se repiten indefinidamente alguna o algunas cifras
decimales. Si el período aparece inmediatamente después de la coma se denominan expresiones
decimales periódicas puras y si el período aparece luego de una parte no periódica expresiones
decimales periódicas mixtas.
¿Cómo realizamos el pasaje de una expresión decimal a una fracción? Esto depende de la
naturaleza de la expresión decimal, es decir si es exacta o periódica.
Expresión exacta
La fracción resultante tiene como numerador el número decimal, sin la coma y el denominador se
forma con la unidad seguida de ceros, tantos como cifras decimales tenga. (Recordemos que
trabajamos con un sistema numérico de base decimal).Observemos los ejemplos:
35
1256
3,5 =
12,56 =
10
100
Expresión periódica (mixta o pura) a fracción
En este caso la fracción equivalente a la expresión decimal se obtiene mediante la siguiente regla:
Numerador: es la diferencia entre el numerador original, sin la coma decimal, menos el número que
conforman aquéllos que no forman parte del período, también sin coma decimal.
Denominador: es el número formado por tantos “9” como cifras tenga el período, seguidos de tantos
“0”como cifras tenga el no período,( si lo hubiera).
Ejemplos:
) 13 − 1 12 4
1,3 =
=
=
9
9 3
2, 36 =
) 236 − 23 213
2,36 =
=
90
90
3,0254 =
236 − 2 234 26
=
=
99
99 11
30254 − 302 29952 832
=
=
9900
9900 275
Operaciones en Q:
Dados dos números racionales, recordaremos cómo se opera con ellos
Suma o resta:
Para sumar o restar dos fracciones, se debe tener en cuenta si tienen o no el mismo denominador.
• En el caso de que los denominadores sean iguales, se opera con los numeradores para
encontrar el numerador y se coloca el mismo denominador en el resultado:
1
1 2 3 ⎛1 3⎞ 2
2 2
2 −6+4
2/
1
=− 3 =−
Ejemplo: + − = ⎜ − ⎟ + = − + = −1 + =
2 3 2 ⎝2 2⎠ 3
2 3
3
6
3
6/
• Si los denominadores son distintos, se busca m que es el mínimo común múltiplo (mcm), o
CM. Borré
Pág. 5
UNSa- Facultad de Ingeniería
CIU 2011
ÁREA MATEMÁTICA
Unidad 1: Conjuntos numéricos
común múltiplo menor de los denominadores. En el caso de números primos m es el
producto de ellos. Se procede con el siguiente algoritmo:
a c (m / b.)a ± (m / d ).c
± =
b d
m
Ejemplo:
2 4 (15 / 3)2 + (15 / 5).4 22
+ =
=
3 5
15
15
2 1 (12 / 3)2 + (12 / 12).1 9 3
+
=
=
=
3 12
12
12 4
Recordemos que el mcm de una cantidad de números dada, previa factorización de los mismos en
los números primos consecutivos, se obtiene como el producto de tales factores comunes y no
comunes, elevados a la mayor potencia con que aparecen en la mencionada factorización.
Producto:
Antes de proceder a calcular el resultado, es conveniente simplificar, es decir dividir el numerador
de una fracción con el denominador de la otra, o de la misma, si no era irreductible (es decir,
aplicamos propiedad cancelativa a los factores que intervienen en numerador y denominador).El
resultado es la fracción cuyo numerador es el producto de los numeradores que se multiplican, y el
denominador, el producto de los mismos.
a c a⋅c
⋅ =
b d b⋅d
Ejemplos:
3 5 3 ⋅ 5 15
1 3
3
3/ 1 5 1 5 5
− 2/ 1 3
⋅ =
=
. 2 =− . =−
. = . =
4 7 4 ⋅ 7 28
5 4/
5 2
10
9/ 3 2 3 2 6
Cociente:
Antes de proceder a calcular el resultado, es conveniente transformarlo en producto, previa
simplificación, de modo que:
a
c ad
a c b a
: = =
.
=
d bc
b d c b
d
Ejemplo:
3 5 3. 7 21
: =
=
4 7 4 .5 20
Cuando aparecen potencias de exponente fraccionario, donde el denominador es diferente de 1,
(equivalente a raíces), y la base (o radicando) no es potencia entera de ese valor, el número
resultante no pertenece a Q; por ejemplo: 2 = 21 / 2 ; 3 2 2 = 2 2 / 3 ; aparecen entonces los números
irracionales
1.2.4 Conjunto de Números Irracionales(I):
CM. Borré
Pág. 6
UNSa- Facultad de Ingeniería
CIU 2011
ÁREA MATEMÁTICA
Unidad 1: Conjuntos numéricos
Al conjunto de los números irracionales (I) pertenecen las expresiones con infinitas cifras decimales
no periódicas. Por ejemplo: 2, 3 , π , e , 0,202200222000…..
No pueden expresarse como cociente de dos números enteros.
Operaciones con radicales
A continuación revisaremos algunos conceptos referidos a operaciones que involucren números
irracionales (radicales):
a) Adición y sustracción de radicales:
Dos radicales son semejantes cuando tienen el mismo índice y el mismo radicando. Al sumar o
restar términos que contengan radicales semejantes, podemos obtener una expresión de un solo
término.
Ej. − 2 5 + 3 5 = 5
Se nos puede presentar la situación en la que los radicales no sean semejantes, por ejemplo para
calcular el perímetro de un triángulo en el cual sus lados miden: 18 ; 32 ; 8
En este caso la suma a resolver es.
P = 18 + 32 + 8
Si operamos convenientemente en cada uno de los radicales, podemos obtener radicales semejantes:
P = 2 .3 2 + 2 5 + 2 3
Factorizamos cada radicando:
Descomponemos en potencias de exponente 2:
P = 2.3 2 + 2 2 2 2.2 + 2 2 2
Distribuimos las raíces:
P = 2. 3 2 + 2 2 . 2 2 . 2 + 2 2 . 2
P = 2 .3 + 2 .2 . 2 + 2 . 2 = 3 2 + 4 2 + 2 2 = 9 2
Simplificamos y operamos:
Observamos que, si una vez factorizado el radicando, distribuimos las raíces y expresamos
los factores con exponentes fraccionarios, genéricamente f m/n, con m ≥ n , el exponente al que
queda elevado f fuera de la raíz, es el entero que resulta de efectuar el cociente m:n, y el exponente
al que queda elevado dentro de la raíz es el resto de tal cociente. Ésto se conoce como “extracción
factores fuera de la raíz”, y el camino inverso, “introducción”
P = 2.3 2 + 2 5 + 2 3 = 21 / 2 3 2 / 2 + 2 5 / 2 + 2 3 / 2 = 21 / 2 3 + 2 2 21 / 2 + 21 21 / 2 =
21 / 2 (3 + 4 + 2) = 9 2
b) Multiplicación y división:
• En el caso de que los índices sean iguales, se resuelve con el procedimiento inverso a la
aplicación de la propiedad distributiva (asociativa), o sea:
•
1/ n
a a1/ n ⎛ a ⎞
a . b = a.b = a .b = (a.b)
=
=
=⎜ ⎟
n
b b1 / n ⎝ b ⎠
b
Si los índices son distintos, se busca m que es el mcm de los índices y se procede como en el
siguiente ejemplo:
6
2 .4 3 =
buscamos el mcm (6,4)=12 y hallamos radicales equivalentes a los dados pero de índice 12:
n
n
n
1/ n
1/ n
1/ n
n
a
n
4
2 . = 6.2 21.2 = 12 2 2
3 = 4.3 31.3 = 12 33
Reemplazamos en el ejercicio:
6
CM. Borré
Pág. 7
UNSa- Facultad de Ingeniería
CIU 2011
ÁREA MATEMÁTICA
Unidad 1: Conjuntos numéricos
2 .4 3 = 12 2 2 .12 33 = 12 2 2.33 = 12 108
En forma análoga, podemos trabajar si en vez de raíces utilizamos exponentes fraccionarios,
como hicimos anteriormente.
Las propiedades que se usaron se verán con más detalle mas adelante.
c) Racionalización de denominadores:
En algunas ocasiones, aparecen radicales en los denominadores de alguna expresión fraccionaria.
La racionalización de denominadores consiste en obtener una expresión equivalente a la dada, en la
cual el denominador es un número racional, o sea sin radicales.
Sea n = a /(b m / n ), m < n El modo consiste en multiplicar y dividir n por b1-(m/n)=b(n-m)/n
6
Primer caso: Radical puro en el denominador:
Ejemplo:
3
3
21−1 / 2 3.21 / 2 3 2 3
= 1 / 2 × 1−1 / 2 =
=
=
2
2
2
2
21
2 2
Ejemplo:
5
b 5− 4
a.5 b1
a.5 b
5
5
b
b 4 5 b 4 5 b 5− 4
b5
Si m>n, se extraen factores y luego se aplica la técnica
a
a
=
×
=
=
Segundo caso: Suma o diferencia de radicales con índice 2 en el denominador.
En este caso, multiplicamos y dividimos por el conjugado del denominador, es decir, por los
mismos términos, ahora con el signo cambiado: si es suma, multiplicamos y dividimos por la
diferencia; si es diferencia, multiplicamos y dividimos por la suma. Estamos aplicando la propiedad
uniforme.
(
a
b+ c
=
) (
a
b+
Ejemplo:
(
3
2+ 5
=
) (
3
2+
(
c) (
x
(
5) (
x
)=
c) ( b)
b− c
b−
2
)=
5) ( 2 )
2− 5
2−
2
a b −a c
+ b c− b c−
3 2 −3 5
+ 2 5− 2 5−
( 5)
2
=
( c)
3
2
(
=
2− 5
2 −5
a b −a c
b −c
) = 3/(
2− 5
− 3/
) =−
(
)
2− 5 = 5− 2
1.2.5 Conjunto de Números Reales:
Todos los números mencionados hasta el presente pertenecen a un conjunto más amplio,
denominado Conjunto de Números Reales y que completa la recta numérica.. Esquemáticamente:
CM. Borré
Pág. 8
UNSa- Facultad de Ingeniería
CIU 2011
ÁREA MATEMÁTICA
Unidad 1: Conjuntos numéricos
R
I
Q
Z
N
Es decir que N⊂Z, Z⊂Q y Q⊂R. También se ve en el gráfico que Q ∪Irr = R y Q ∩Irr = φ
Los números reales se pueden representar sobre una línea recta, conocida como la recta real.
Decimos que existe una correspondencia biunívoca (ver luego Unidad Funciones) entre puntos de
la recta y números reales.
Aún en R, existe una operación que no está definida: la raíz de índice par de radicando negativo o,
en otras palabras, las potencias de base negativa con índice fraccionario de denorminador par.
Aparece así un nuevo conjunto de números, los Complejos (C), dentro de los que se incluyen los
reales. Su representación ya no corresponde a una recta, sino a un plano-plano de Argand o
complejo-, pero este conjunto de números queda fuera del alcance de este curso.
I
R
Q
Z
N
C
Imag
Es decir que N⊂Z, Z⊂Q, Q⊂R y R ⊂ C ;R ∪ Im ag = C , R ∩ I mag = φ
ASÍ QUE POR DEFECTO, SIEMPRE QUE HABLEMOS DESDE AHORA NOS
REFERIREMOS A NÚMEROS REALES.
Es importante destacar, no obstante, que la división por cero no está definida en ningún conjunto
numérico: NO LO OLVIDEMOS!
1.3 SUBCONJUNTOS DE R: INTERVALOS REALES
Es muy frecuente que se usen intervalos de la recta real. A continuación los definimos.
Sean a,b ε R, tal que a < b, se define:
Intervalo cerrado [a,b]: [a, b] = {x / x ∈ R ∧ a ≤ x ≤ b}
Intervalo abierto (a,b): (a, b) = {x / x ∈ R ∧ a < x < b}
Intervalo semicerrados o semiabiertos:
CM. Borré
Pág. 9
UNSa- Facultad de Ingeniería
CIU 2011
ÁREA MATEMÁTICA
Unidad 1: Conjuntos numéricos
[a, b) = {x / x ∈ R ∧ a ≤ x < b}
(a, b] = {x / x ∈ R ∧ a < x ≤ b}
Los que son semirrectas, o sea no tienen principio o no tienen fin:
[a, ∞) = {x / x ∈ R ∧ x ≥ a}
(a, ∞) = {x / x ∈ R ∧ x > a}
(−∞, b] = {x / x ∈ R ∧ x ≤ b}
(−∞, b) = {x / x ∈ R ∧ x < b}
En las gráficas se muestra la representación de estos conjuntos sobre la recta real:
1.4 OPERACIONES CON NÚMEROS REALES. PROPIEDADES
Cuando operamos con números reales (sumamos, restamos, etc.) hay ciertas reglas que debemos
respetar, este conjunto de reglas reciben el nombre de propiedades. Las mismas se pueden comparar
con el reglamento de un deporte, si se desconoce el mismo no se puede practicar el deporte en un
campo de juego pues seguramente no sabríamos como desenvolvernos.
1.4.1 Suma:
Ley de cierre: ∀a, b ∈ R : a + b ∈ R
Propiedad Conmutativa: ∀a, b ∈ R : a + .b = b + .a
Propiedad Asociativa: ∀a, b, c ∈ R : (a + b) + c = a + (b + c)
Existencia del elemento neutro para la suma: ∀a ∈ R, ∃0 ∈ R : a + 0 = 0 + a = a
Existencia del elemento opuesto: ∀a ∈ R ≠ 0 ∃(−a ) ∈ R : a + (−a ) = (−a ) + a = 0
Nota: recordemos que en R, la diferencia es la suma del opuesto:
a−b = c ⇔ c+b = a
a: minuendo; b: sustraendo
a − b = a + ( −b ) .
En este caso, el 0 pasa a ser elemento neutro sólo como sustraendo.
LOS SIGNOS (+) Y (-) SEPARAN TÉRMINOS.
1.4.2 Producto:
Ley de cierre: ∀a, b ∈ R : a.b ∈ R
Propiedad Conmutativa: ∀a, b ∈ R : a.b = b.a
Propiedad Asociativa: ∀a, b, c ∈ R : (a.b).c = a.(b.c) = a.b.c
CM. Borré
Pág. 10
UNSa- Facultad de Ingeniería
CIU 2011
ÁREA MATEMÁTICA
Unidad 1: Conjuntos numéricos
Existencia del elemento neutro para el producto: ∀a ∈ R, ∃1 ∈ R : a.1 = 1.a = a
Existencia de elemento absorbente para el producto: ∀a ∈ ℜ∃0 ∈ ℜ / a.0 = 0.a = 0
Existencia del elemento inverso: ∀a ∈ R, a ≠ 0 ∃a −1 ∈ R : a.a −1 = a −1 .a = 1
Nota: observemos que el cociente, para b ≠ 0 , es equivalente al producto por el inverso
multiplicativo (o recíproco) del divisor.
a / b = c + r / b, b ≠ 0 ⇔ (c + r / b) = a
a:dividendo, b: divisor, c: cociente, r:resto
a
⎛1⎞
b ≠ 0, = a.⎜ ⎟ = a.b −1
b
⎝b⎠
En este caso, 0 es elemento absorbente como dividendo, y 1 es elemento neutro como
divisor; sin embargo, no es conmutativo, pero sí asociativo, y distributivo sólo “ a la
izquierda”.
PRODUCTO Y COCIENTE NO SEPARAN TÉRMINOS
1.4.3 Distributivas:
Producto respecto de la suma: distibuye “a la derecha” c.(a+b) = c.a + c.b
,y “ a la izquierda” (a + b).c = a.c + b.c
a+b a b
= +
Cociente respecto de la suma:
c
c c
Recuerden que no es válido distribuir cuando la suma esta en el denominador:
a
a a
≠ +
b+c b c
En otras palabras, distribuye sólo “a la izquierda”
1.4.4 Propiedades de la igualdad
∀a ∈ R, a = a (prop. reflexiva)
∀a, b ∈ R, a = b ⇔ b = a (prop. simétrica)
∀a, b ∈ R, a = b ∧ b = c ⇒ a = c (prop. transitiva)
1.4.5.Propiedades de orden
Axiomas (postulados que se aceptan sin demostrar)
1- ∀a ∈ ℜ, a > 0 ∨ a = 0 ∨ a < 0
2-La suma de dos números positivos es positiva.
3-El producto de dos números positivos es positivo.
4-El número real a es negativo si y sólo si (–a) es positivo.
Propuesta: escribe en forma simbólica los postulados 2 a 4, y el 1 en forma coloquial.
∀a, b ∈ ℜ, a < b ∨ a > b ∨ a = b (prop. de tricotomía)
∀a, b, c ∈ ℜ, a < b ∧ b < c ⇒ a < c (prop. transitiva del orden)
1.4.6 Propiedades de las operaciones sobre igualdades
Ley uniforme para la suma: ∀a, b, c ∈ R : a = b ⇒ a + c = b + c
Ley uniforme para el producto: ∀a, b, c ∈ R : a = b ⇒ a.c = b.c :
Ley cancelativa para la suma: ∀a, b, c ∈ R : a + c = b + c ⇒ a = b
CM. Borré
Pág. 11
UNSa- Facultad de Ingeniería
CIU 2011
ÁREA MATEMÁTICA
Unidad 1: Conjuntos numéricos
Ley cancelativa para el producto: ∀a, b, c ∈ R, c ≠ 0 : a.c = b.c ⇒ a = b
Ley de anulación para el producto: a, b ∈ R, a.b = 0 ⇒ a = 0 ∨ b = 0
1.4.7 Propiedades de las operaciones sobre desigualdades
∀a, b, c ∈ R : a < b ⇒ a ± c < b ± c
∀a, b, c ∈ R : a < b, c > 0 ⇒ a.c < b.c
∀a, b, c ∈ R : a < b, c < 0 ⇒ a.c > b.c
∀a, b, c ∈ R : a + c < b + c ⇒ a < b
∀a, b, c ∈ R : a.c < b.c, c > 0 ⇒ a < b
∀a, b, c ∈ R : a.c < b.c, c < 0 ⇒ a > b
En forma análoga, se verifican para las otras desigualdades, estrictas o amplias.
1.4.8 Reglas de signos: de lo visto anteriormente, se deduce que, ∀a, b ∈ R se cumple:
-(-a)=a
(-a).b= - (a.b) = a.(-b)
(-1).a= - a
Recordemos que ∀a, b ∈ ℜ ∧ a, b > 0
a.b > 0
(− a)(−b) > 0
a.(−b) < 0
(− a).b < 0
Esto se hace extensivo a desigualdades amplias.
Ejemplo: en base a estas propiedades, podemos deducir que:
∀a, b ∈ ℜ, a.b ≥ 0 ⇔ (a ≥ 0 ∧ b ≥ 0) ∨ (a ≤ 0 ∧ b ≤ 0)
,porque de acuerdo a la regla de los signos, para que un producto de dos factores sea positivo o
igual a cero, ambos deben ser del mismo signo (ambos positivos o ambos negativos
simultáneamente), o alguno de ellos iguales a cero.
1.5 POTENCIA Y RADICACION DE NÚMEROS REALES
1.5.1 Definición de potencia
Si a es un número real, distinto de 0, y n es un número natural, se define:
a n = a1
.a4
.a4
.a2
..........
.a
44
3
n − veces
an se lee: “a elevado a la n”; a se denomina base y n el exponente. Además: a 0 = 1
a −1 =
1
a
Por lo tanto se cumple también que:
CM. Borré
Pág. 12
UNSa- Facultad de Ingeniería
CIU 2011
ÁREA MATEMÁTICA
Unidad 1: Conjuntos numéricos
1
an
Observemos que 0 0 tampoco está definido en los conjuntos numéricos.
a −n =
1.5.2 Algunas propiedades de la potencia:
1. Producto de potencias de igual base: a n. a m = a n + m
2.Cociente de potencias de igual base: a n : a m = a n −m
3 Potencia de potencia: (a n ) m = a n.m
4.Distributiva de la potencia respecto del producto y del cociente:
(a . b )
n
n
=a .b
n
an
⎛a ⎞
⎜ ⎟ = n
⎝b ⎠
b
n
si b ≠ 0
La potenciación no es distributiva respecto a la suma o la diferencia. Es decir
( a ± b) n ≠ a n ± b n
1.5.3 Radicación
Si n es par , la raíz solo esta definida para números positivos, es decir:
Dado a>0 n a = b ⇔ b n = a, b ≥ 0
Si n es impar , la raíz esta definida para cualquier real, es decir:
Dado a∈R n a = b ⇔ b n = a
a: radicando, n: índice; por defecto-es decir, cuando n no aparece, se trata de “raíz cuadrada”
(implícitamente, n=2)
Ejemplos:
4=2
− 9 =∉ R
5
− 32 = −2
3
8=2
4
16 = 2
− 6 =∉ R
Una raíz se puede escribir como potencia de exponente racional, y convenimos que:
4
n
( )
a = a1 / n , n ≠ 0
m
a m = n a = ( a 1 / n ) m = ( a m )1 / n = a m / n , n ≠ 0
Observamos así que la radicación puede considerarse como una potencia de exponente fraccionario,
y valen pues las propiedades vistas para ésta; es decir:
n
1.5.4 Algunas propiedades de la Radicación
1. Distributiva respecto del producto y del cociente:
a na
n
n
a.b = n a .n b
=
,b ≠ 0
b nb
2. Raíz de raíz:
a = n.m a
3. Amplificación y simplificación de índices (r≠0):
m n
CM. Borré
Pág. 13
UNSa- Facultad de Ingeniería
CIU 2011
n
ÁREA MATEMÁTICA
Unidad 1: Conjuntos numéricos
a m = n.r a m.r
n
a m = n:r a m:r
La radicación no es distributiva respecto a la suma o la diferencia. Es decir:
a±b ≠ n a ±n b
Si tenemos una potencia, como radicando en una raíz de índice par, podemos escribir:
(−2) 2 = (−2) 2.1 / 2 = −2 que es equivalente a simplificar índice con exponente y esto no es correcto
porque si operamos sin simplificar, el resultado obtenido es 2 (positivo). Vale decir, la radicación
no cumple la propiedad cancelativa
n
1.6- VALOR ABSOLUTO DE UN NÚMERO REAL
Hemos visto que los números reales se representan en la recta numérica.
Se puede observar que la distancia del
número 4 hasta el 0 es igual a 4 y que la
distancia del número -4 hasta el 0,
también es igual a 4. O sea, la distancia de un punto al cero no tiene en cuenta de que lado del cero
esté el número.
Si consideramos a la distancia de un número hasta cero como un valor positivo, definimos a ésta
como el valor absoluto del número; se indica con dos barras que abarcan al mismo.
Por ejemplo: 4 = 4
−4 =4
3 =3
−3 = 3
Podemos apreciar que el valor absoluto de un número es el mismo número, si éste es positivo o 0, y
el opuesto, si es negativo.
Esto se puede formalizar mediante la siguiente definición:
⎧ x si x ≥ 0
x =⎨
⎩− x si x < 0
Algunas propiedades de valor absoluto:
x ≥0
−x = x
x. y = x . y
x
x
=
y
y
x+ y ≤ x + y
x− y ≥ x − y
x ≤ a, a > 0 ⇒ − a ≤ x ≤ a
x ≥ a, a > 0 ⇒ x ≤ − a ∨ x ≥ a
Igualdad importante:
Con el concepto de valor absoluto de un número real, podemos volver sobre el problema planteado
CM. Borré
Pág. 14
UNSa- Facultad de Ingeniería
CIU 2011
ÁREA MATEMÁTICA
Unidad 1: Conjuntos numéricos
en el apartado 1.5.4, sobre la simplificación de radicales y directamente escribir la siguiente
igualdad, válida para todo numero real, con n=2 ( o par):
x = n xn
OTROS
-Recordemos que los símbolos : =,>,<, ≥, ≤ , separan miembros.
-Recordemos también que para el producto en vez de “x”(por), usamos “.”(punto) o más
frecuentemente, ningún símbolo.
-A diferencia de “la coma decimal” (,) que aprendimos en la escuela, es más frecuente emplear el
punto (.) para indicar decimales, y las comas para separar miles (sistema americano); esto se ha
difundido ampliamente por la proliferación de software y calculadoras, donde el punto indica
decimales, y no se usan comas para separar los miles. A modo de ejemplo de esta diferencia, tené
en cuenta que “billion”, en inglés, corresponde a mil millones (1 seguido de nueve 0), aunque en
nuestro español, “billón” es un millón de millones (1 seguido de doce 0).No confundir.
-Las operaciones de suma y diferencia separan términos, no así productos, cocientes ni potencias u
otras operaciones más complejas. La secuencia “natural” con que se resuelven ejercicios
combinados son: primero potencias-u otras más complejas-, luego productos y cocientes y
finalmente sumas y diferencias. Si queremos o necesitamos “alterar” este orden, debemos usar
paréntesis, corchetes y llaves, en orden sucesivo de resolución.
Observa en los siguientes ejemplos que, pese a la similitud, son operaciones diferentes, con
resultados diferentes.
0.2 2.5/4+3-1/2+2=0.2.32/4+3-0.5+2=0.64/4+3-0.5+2=0.16+2.5+42=4.66
(0.2.2)5/4+3-1/(2+2)=(0.4)5+3-1/4=0.01024+3-.25=2.76024
(0.2 2.5/4+3-1)/2+2=3.8
-Cuando emplees calculadora o algún software, fijate en el manual, porque en operaciones
combinadas a veces deben usarse paréntesis “anidados”-en vez de corchetes y llaves-, que
usualmente serían innecesarios, pero los mecanismos de cálculo de estos equipos-algoritmos-exigen
que se coloquen, porque de otro modo resuelven sucesivamente de izquierda a derecha.
-Respecto a la bibliografía, se especificarán las citas al final del material, con todos los detalles;
como adelanto, algunos autores son Stewart, Leithold (los de Matemática básica), Allendoerfer &
Oakley, etc.
CM. Borré
Pág. 15