C u r s o : Matemática Material N° 05
Anuncio
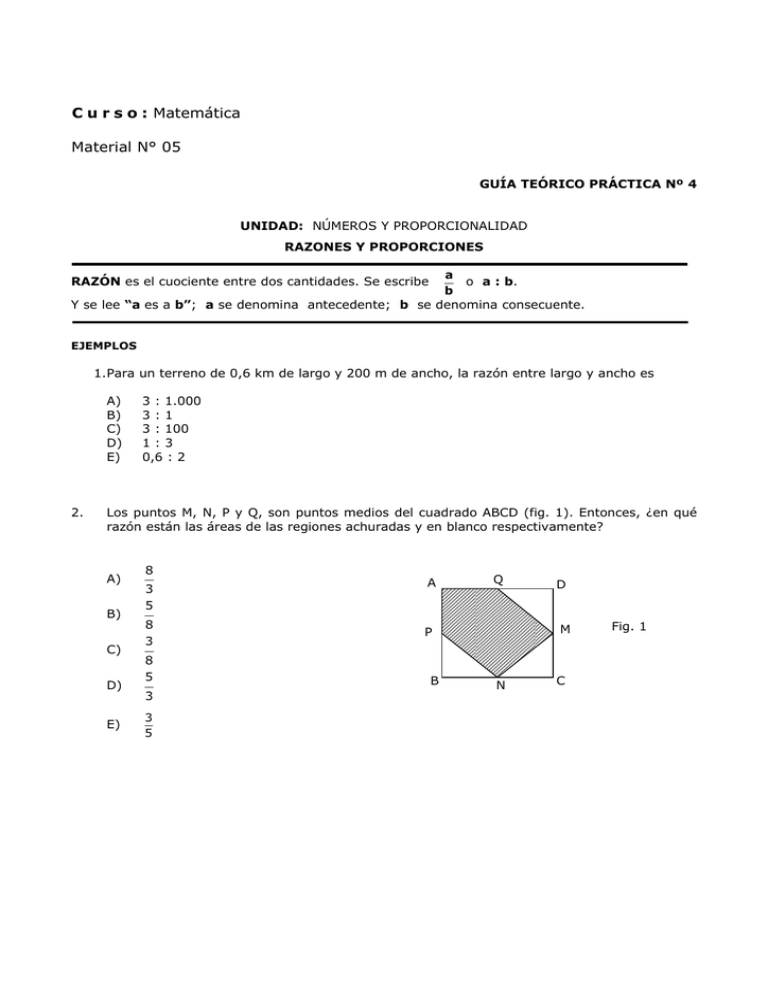
C u r s o : Matemática Material N° 05 GUÍA TEÓRICO PRÁCTICA Nº 4 UNIDAD: NÚMEROS Y PROPORCIONALIDAD RAZONES Y PROPORCIONES a o a : b. b Y se lee “a es a b”; a se denomina antecedente; b se denomina consecuente. RAZÓN es el cuociente entre dos cantidades. Se escribe EJEMPLOS 1. Para un terreno de 0,6 km de largo y 200 m de ancho, la razón entre largo y ancho es A) B) C) D) E) 2. 3 : 1.000 3:1 3 : 100 1:3 0,6 : 2 Los puntos M, N, P y Q, son puntos medios del cuadrado ABCD (fig. 1). Entonces, ¿en qué razón están las áreas de las regiones achuradas y en blanco respectivamente? A) B) C) D) E) 8 3 5 8 3 8 5 3 3 5 A Q M P B D N C Fig. 1 PROPORCIÓN es la igualdad de dos razones. Se escribe Y se lee “x es a a x y = a b ó x:a= y:b como y es a b”; x y b se denominan extremos; a e y se denominan medios. TEOREMA FUNDAMENTAL En toda proporción, el producto de los extremos es igual al producto de los medios. (x : a = y : b) Ù (x · b = y · a) OBSERVACIÓN: Si x : a = y : b, entonces existe una constante k, denominada constante de proporcionalidad, tal que: x = ka , y = kb ; k ≠0 EJEMPLOS 1. Si u : v = 3 : 10 y u : w = 1 : 2 , entonces ¿cuál de las siguientes alternativas es FALSA, sabiendo que v = 30? A) B) C) D) E) 2. u2 = 81 w – v = -12 w =9 2 2w = 36 u – v = 21 El valor de x en la proporción A) B) C) D) E) x −2 x +1 = 3 4 -1 -3 -5 3 11 2 es SERIE DE RAZONES es la igualdad de más de dos razones. La serie de razones x a = y b = z c también se escribe como x:y:z = a:b:c OBSERVACIONES : 2 2 x+y+z x y z = = = =k a+b+c a b c x a y b = = , Si y y b z c entonces x:y:z = a:b:c EJEMPLOS 1. Si A) B) C) D) E) 2. 3 3 5 3 6 : : : : : y b : c = 5 : 9 , entonces a : c : b = 9 : 10 5: 9 9: 3 9: 5 18 : 5 Las edades de tres hermanas: María, Carmen y Lucía, son entre sí como 2 : 5 : 3. Si sus edades suman 30 años, entonces la edad de Lucía es A) B) C) D) E) 3. a:b=3:5 15 años 9 años 6 años 3 años 1 año r 3 = y s 5 verdadera(s)? Si I) II) III) A) B) C) D) E) r 9 = , entonces ¿cuál(es) de las siguientes afirmaciones es(son) t 10 r : t = 3 :10 3 t = s 2 2r : s : 3t = 6 : 5 : 10 Sólo II Sólo III Sólo II y III I, II y III Ninguna de ellas 3 PROPORCIONALIDAD DIRECTA Dos variables, x e y, son directamente proporcionales si el cuociente entre sus valores correspondientes es constante. x x1 x x = 2 = 3 = ........... = n = k y3 y1 y2 yn Así por ejemplo, en la tabla de la figura 1, directamente proporcionales. Por lo tanto se deduce que las cantidades ubicadas en las filas A y B son A 3 4 5 x B 9 12 15 y Fig. 1 x 1 = y 3 OBSERVACIONES : 2 2 En una proporción directa, si una cantidad aumenta (disminuye) n veces, la otra aumenta (disminuye) el mismo número de veces. El gráfico de una proporcionalidad directa corresponde a una línea recta que pasa por el origen (fig. 2). Y Recta yn y3 y2 y1 Fig. 2 x1 x2 x3 xn X EJEMPLOS 1. A y B son magnitudes directamente proporcionales. Respecto a la siguiente tabla 5 30 A B A) B) C) D) E) 7 7 6 8 9 y y y y y x 42 15 y los valores de x e y son respectivamente 90 60 72 90 54 4 2. Si 2x varía directamente con y e y = 4 cuando x = 3 , entonces ¿cuál es el valor de 2x cuando y = 16? A) B) C) D) E) 3. 1 12 1 3 32 24 12 Según el gráfico de la figura 3, Entonces, ¿cuál es el valor de a? A) B) C) D) E) x e y 1 3 3 6 9 12 son magnitudes directamente proporcionales. y a 6 Fig. 3 2 4. 3 x Dos obreros, A y B, reciben como pago por un trabajo $ 275.000. ¿Cuánto le toca a cada uno si A trabajó 2 días y B trabajó 3 días? A A) B) C) D) E) B $ 137.500 $ 137.500 $ 91.666 $ 183.334 $ 55.000 $ 220.000 $ 110.000 $ 165.000 Ninguna de las anteriores 5 PROPORCIONALIDAD INVERSA Dos variables, x e y, son inversamente proporcionales si el producto entre sus valores correspondientes es constante x1 · y1 = x2 · y2 = x3 · y3 = ..........= xn · yn = k k : constante Así por ejemplo, en la tabla de la figura 1, las cantidades ubicadas en las filas inversamente proporcionales A 2 3 5 x Fig. 1 15 10 6 y B A y B son Por lo tanto se deduce que x · y = 30 OBSERVACIONES : 2 2 En una proporcionalidad inversa, si una cantidad aumenta (o disminuye) n veces, la otra disminuye (o aumenta) el mismo número de veces. El gráfico de una proporcionalidad inversa corresponde a una hipérbola equilátera (fig. 2). Y y1 y2 y3 Fig. 2 yn x 1 x2 x3 xn X EJEMPLOS 1. Las cantidades ubicadas en las columnas A y B, en la tabla de la figura 3, son inversamente proporcionales. ¿Cuál es el valor de M + N? A 6 4 N A) B) C) D) E) B 3 M 18 38 36 5,5 5 4,5 6 Fig. 3 2. Las variables x e y son inversamente proporcionales. Cuando x vale 60, y vale 90. ¿Cuánto vale x, cuando y vale 120? A) B) C) D) E) 3. 30 40 45 60 90 De acuerdo a la información entregada en el gráfico de la figura 4, el cual representa una hipérbola, ¿cuál es el valor de C – D? A) B) C) D) E) -8 -4 4 8 Ninguna de las anteriores y D Fig. 4 4 2 2 4. C 8 x 8 empleados hacen un trabajo en 20 días. Para hacer el mismo trabajo en 5 días, ¿cuántos empleados más se necesitarían? A) B) C) D) E) 2 12 16 24 32 7 PROPORCIONALIDAD COMPUESTA Sea A una variable directamente proporcional a la variable B y al mismo tiempo inversamente proporcional a la variable C, entonces se cumple que para sus valores correspondientes: A1 · C1 B1 = A2 · C2 B2 = A 3 · C3 B3 = ......... = A n · Cn Bn =k k : constante EJEMPLOS 1. En un taller de costura, 6 mujeres cosen 30 trajes en 8 horas de trabajo. ¿Cuántos trajes terminarán en 6 horas, si trabajan 16 mujeres? A) B) C) D) E) 2. Si 30 hombres pavimentan 150 m de una carretera en 12 días, trabajando 8 horas diarias, ¿cuántos metros pavimentarían 16 hombres en 18 días, trabajando la misma cantidad de horas diarias? A) B) C) D) E) 3. 8 15 20 60 106 421,9 187,5 120,0 53,3 4,8 Una familia compuesta de 4 personas gasta mensualmente $ 380.000. ¿Cuántas personas podrían vivir 16 días, en igualdad de condiciones, con $304.000? A) B) C) D) E) 2 3 4 5 6 8 EJERCICIOS 1. En la tabla de la figura 1, A y B son magnitudes directamente proporcionales. ¿Cuáles son los valores de x e y , respectivamente? A) B) C) D) E) 2. 72 60 72 2 72 3 5 12 20 40 A 7 x 12 B 42 48 y Fig. 1 Si actualmente sus edades están en la razón años años años años años Las cantidades a2 y b son inversamente proporcionales. Si para a = 2 , se obtiene b = 3 , 4 entonces ¿cuál sería el valor de a , asociado a b = ? 3 A) B) C) D) E) 4. y y y y y Cuando nació Pedro, Mario tenía 8 años. 3 : 5, ¿qué edad tiene Mario? A) B) C) D) E) 3. 8 8 7 8 6 Si A) B) C) D) E) 1 2 2 3 3 4 3 2 3 x:y:z=4:3:2 y 2x + 4y – 3z = 28 , entonces el valor de y es 2 3 4 6 8 9 5. Al dividir 253 en partes proporcionales a los números 2, 5, 7 y 9, ¿cuál es la parte menor? A) B) C) D) E) 6. Hernán, Miguel y Osvaldo compraron un número de rifa y cuyos aportes fueron: Hernán $ 800, Miguel $ 500 y Osvaldo $ 700. Si obtuvieron un premio de $ 280.000, ¿cuánto le correspondió del premio a Miguel al realizarse el reparto en forma proporcional a lo aportado? A) B) C) D) E) 7. $ $ $ $ $ 50.000 70.000 80.000 98.000 112.000 En una guarnición hay 4.800 soldados con alimentos para 48 días. Si la dotación disminuyera a 3.200 hombres, ¿para cuántos días alcanzarían los alimentos? A) B) C) D) E) 8. 11 22 77 99 121 80 72 64 60 32 Si b kilos de clavos valen $ a , entonces A) B) C) D) E) 1 kilo valdrá 2 2ab a 2 b 2a 2b a a 2b 10 9. En el gráfico de la figura 2, x e y son cantidades directamente proporcionales. Entonces, el valor de a – 1 es y A) B) C) D) E) 1,5 2,5 3,5 4,0 5,0 7 5 Fig. 2 a a+1 x 10. El gráfico de la figura 3, muestra la hipérbola que resultó del estudio que se hizo en una campaña militar, en que se determinó la cantidad de días que dura cierta cantidad de alimentos, de acuerdo al número de soldados que los consumen. En base a la información proporcionada por este gráfico, se puede deducir que A) B) C) D) E) p + q = 54 t = 72 t>q t<p t = 4p Cantidad de días t Fig. 3 6 4 2 2 11. p q Cantidad de soldados Si 10 obreros construyen una casa en 6 meses, ¿cuánto tiempo se demorarían 12 obreros en construir una casa similar, trabajando el mismo número de horas al día? A) B) C) D) E) 12. 12 7 6 5 4 4 meses meses meses meses meses y 6 días y 6 días y 24 días y 12 días Si un sitio rectangular de 24 metros de frente por 45 metros de fondo, vale $ 360.000, ¿cuánto valdría otro sitio rectangular de 32 metros de frente por 27 metros de fondo? A) B) C) D) E) $ $ $ $ $ 25.920 28.800 45.000 288.000 450.000 11 13. En un recipiente hay 16 litros de una mezcla que contiene agua y alcohol. Si 7 litros de esta mezcla son de alcohol, ¿cuántos litros de agua deberán agregarse a la mezcla, para que la cantidad de alcohol y el total de la mezcla queden en la razón 1 : 3? A) B) C) D) E) 14. 15. 4 5 11 12 21 Con respecto a la tabla de la figura 4, ¿cuál es el valor de x + y + z? (1) A y B son magnitudes directamente proporcionales. (2) x2 = 64 A) B) C) D) E) (1) por sí sola (2) por sí sola Ambas juntas, (1) y (2) Cada una por sí sola, (1) ó (2) Se requiere información adicional y 3z = 45 A B 5 30 x z 30 48 90 y Fig. 4 ¿A cuántos billetes de color verde, equivale un billete de color azul? (1) Un billete de color azul equivale a mil unidades. (2) Un billete de color verde equivale a dos billetes de color rojo, y un billete de color rojo equivale a diez unidades. A) B) C) D) E) (1) por sí sola (2) por sí sola Ambas juntas, (1) y (2) Cada una por sí sola, (1) ó (2) Se requiere información adicional RESPUESTAS Ejemplos Págs. 1 2 3 4y5 6y7 8 1 2 B E D A C D D E B E C C 3 C D B E CLAVES PÁG. 9 4 1. 2. 3. 4. 5. D D 12 A D E D B 6. B 7. E 8. E 9. A 10. A 11. 12. 13. 14. 15. C D B D C









