Estadística bidimensional
Anuncio
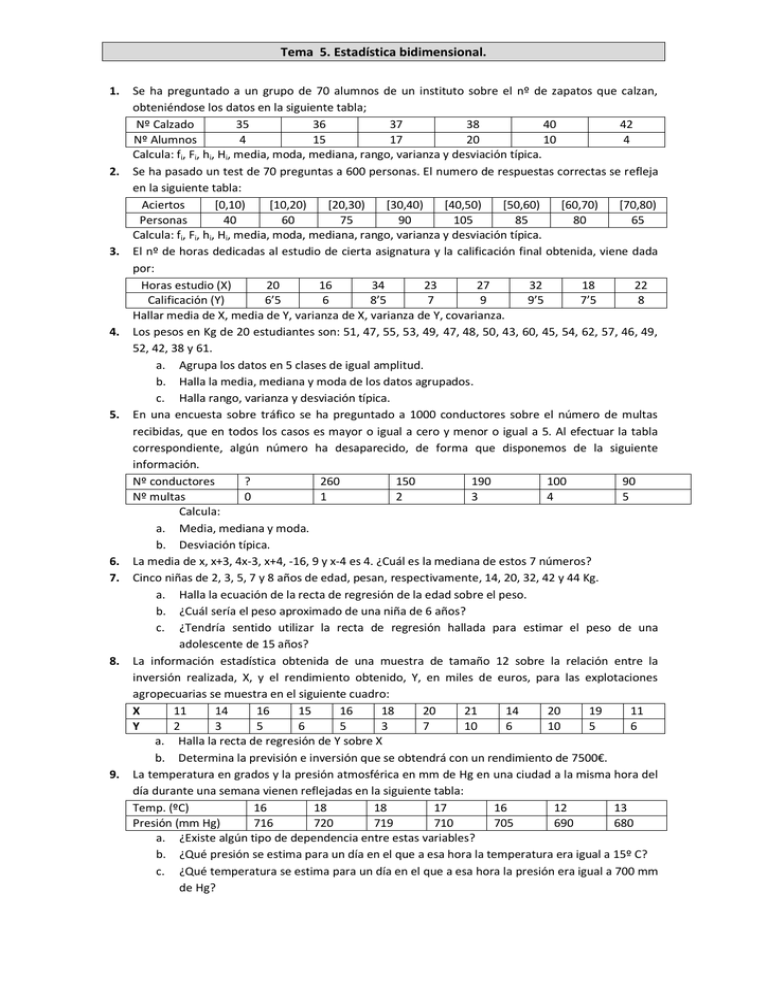
Tema 5. Estadística bidimensional. 1. 2. 3. 4. 5. 6. 7. 8. 9. Se ha preguntado a un grupo de 70 alumnos de un instituto sobre el nº de zapatos que calzan, obteniéndose los datos en la siguiente tabla; Nº Calzado 35 36 37 38 40 42 Nº Alumnos 4 15 17 20 10 4 Calcula: fi, Fi, hi, Hi, media, moda, mediana, rango, varianza y desviación típica. Se ha pasado un test de 70 preguntas a 600 personas. El numero de respuestas correctas se refleja en la siguiente tabla: Aciertos [0,10) [10,20) [20,30) [30,40) [40,50) [50,60) [60,70) [70,80) Personas 40 60 75 90 105 85 80 65 Calcula: fi, Fi, hi, Hi, media, moda, mediana, rango, varianza y desviación típica. El nº de horas dedicadas al estudio de cierta asignatura y la calificación final obtenida, viene dada por: Horas estudio (X) 20 16 34 23 27 32 18 22 Calificación (Y) 6’5 6 8’5 7 9 9’5 7’5 8 Hallar media de X, media de Y, varianza de X, varianza de Y, covarianza. Los pesos en Kg de 20 estudiantes son: 51, 47, 55, 53, 49, 47, 48, 50, 43, 60, 45, 54, 62, 57, 46, 49, 52, 42, 38 y 61. a. Agrupa los datos en 5 clases de igual amplitud. b. Halla la media, mediana y moda de los datos agrupados. c. Halla rango, varianza y desviación típica. En una encuesta sobre tráfico se ha preguntado a 1000 conductores sobre el número de multas recibidas, que en todos los casos es mayor o igual a cero y menor o igual a 5. Al efectuar la tabla correspondiente, algún número ha desaparecido, de forma que disponemos de la siguiente información. Nº conductores ? 260 150 190 100 90 Nº multas 0 1 2 3 4 5 Calcula: a. Media, mediana y moda. b. Desviación típica. La media de x, x+3, 4x-3, x+4, -16, 9 y x-4 es 4. ¿Cuál es la mediana de estos 7 números? Cinco niñas de 2, 3, 5, 7 y 8 años de edad, pesan, respectivamente, 14, 20, 32, 42 y 44 Kg. a. Halla la ecuación de la recta de regresión de la edad sobre el peso. b. ¿Cuál sería el peso aproximado de una niña de 6 años? c. ¿Tendría sentido utilizar la recta de regresión hallada para estimar el peso de una adolescente de 15 años? La información estadística obtenida de una muestra de tamaño 12 sobre la relación entre la inversión realizada, X, y el rendimiento obtenido, Y, en miles de euros, para las explotaciones agropecuarias se muestra en el siguiente cuadro: X 11 14 16 15 16 18 20 21 14 20 19 11 Y 2 3 5 6 5 3 7 10 6 10 5 6 a. Halla la recta de regresión de Y sobre X b. Determina la previsión e inversión que se obtendrá con un rendimiento de 7500€. La temperatura en grados y la presión atmosférica en mm de Hg en una ciudad a la misma hora del día durante una semana vienen reflejadas en la siguiente tabla: Temp. (ºC) 16 18 18 17 16 12 13 Presión (mm Hg) 716 720 719 710 705 690 680 a. ¿Existe algún tipo de dependencia entre estas variables? b. ¿Qué presión se estima para un día en el que a esa hora la temperatura era igual a 15º C? c. ¿Qué temperatura se estima para un día en el que a esa hora la presión era igual a 700 mm de Hg? 10. En la tabla se recogen las puntuaciones de dos pruebas (X, Y) de cinco alumnos. X 6 5 12 8 9 Y 8 5 10 7 10 a. Haz el diagrama de dispersión (nube de puntos) b. Si la recta de regresión de Y sobre X es y=0’63x+2’96, ¿qué puntuación espera en la prueba Y un sujeto que a obtenido una puntuación de 10 en la prueba X? c. Calcula la covarianza de las puntuaciones. 11. A partir de los datos recogidos sobre facturación anual y beneficios anuales en un determinado año sobre un conjunto de 50 grandes empresas europeas, se ha calculado una facturación media de 80 millones de euros y unos beneficios medios de 65 millones a. Teniendo en cuenta esta información, determina la recta de regresión que permite obtener los beneficios en función de la facturación, sabiendo que a partir de ella se han calculado unos beneficios de 59 millones de euros para una empresa que ha facturado 75 millones en 1998. b. ¿Qué signo tendría el coeficiente de correlación lineal entre ambas variables? 12. En un determinado grupo de Bachillerato de un centro de Educación Secundaria, las calificaciones de Matemáticas de 8 alumnos en las evaluaciones 1ª y 2ª están representadas en la siguiente tabla: 1ª Eval. (X) 4 8 3 6 4 9 8 6 2ª Eval. (X) 3 7 3 5 4 7 6 5 a. Calcula el coeficiente de correlación lineal. b. Calcula la recta de regresión de Y sobre X. c. Si un alumno del grupo ha obtenido una calificación de 7’5 en la 1ª evaluación, ¿qué calificación se supone que obtendrá en la 2ª evaluación? 13. Se ha solicitado a un grupo de 50 individuos información sobre el numero de horas ue dedican diariamente a dormir (X) y a ver la televisión (Y). Los resultados vienen dados por la siguiente tabla: X 6 7 8 9 10 Y 4 3 3 2 1 fi 3 16 20 10 1 a. Calcula el coeficiente de correlación lineal entre X e Y, e interprétalo en términos del enunciado. b. Calcula la ecuación de la recta de regresión de Y sobre X. c. Si una persona duerme 8 horas y media, ¿cuántas horas cabe esperar que vea la televisión? d. Sin calcular la recta de regresión de X sobre Y, ¿en qué punto se cortará esta recta con la calculada en el apartado b? e. Si una persona ve la televisión 2 horas, ¿cuánto tiempo cabe esperar que duerma? 14. Los valores de dos variables X e Y se distribuyen según la tabla siguiente: a. Determina el coeficiente de correlación y la X 0 2 4 Y recta de regresión de Y sobre X b. Comenta lo fiables que son las predicciones 1 2 1 3 basadas en esa recta. 2 1 4 2 3 2 5 0