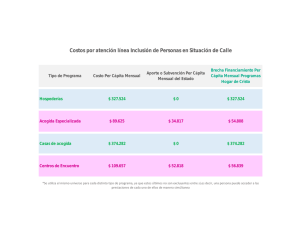
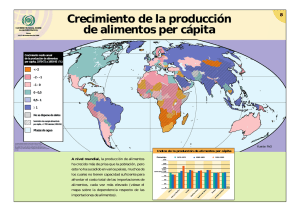
Francisco Félix Caballero Díaz
Anuncio

ÍNDICE DE CONTENIDOS 1. INTRODUCCIÓN ----------------------------------------------------------------------------1 1.1. Historia de la Unión Europea 1.2. Algunas características sociales de los países de la Unión Europea 1.3. Cambio climático 2. OBJETIVOS -----------------------------------------------------------------------------------8 3. VARIABLES Y MÉTODOS ----------------------------------------------------------------9 3.1. Eurostat 3.2. Agencia Europea de Medio Ambiente 3.3. Variables utilizadas en este estudio 3.4. Análisis Multivariante 3.4.1. Análisis Cluster 3.4.2. Análisis Discriminante 3.4.3. Análisis de Correspondencias 3.4.4. Análisis de Componentes Principales 3.4.5. Análisis Factorial 3.5. Software empleado para realizar el análisis de los datos 4. RESULTADOS -------------------------------------------------------------------------------24 4.1. Análisis Cluster 4.2. Análisis Discriminante 4.3. Análisis de Correspondencias 4.4. Análisis de Componentes Principales 4.5. Análisis Factorial 5. CONCLUSIONES ---------------------------------------------------------------------------39 6. REFERENCIAS ------------------------------------------------------------------------------43 1. INTRODUCCIÓN 1.1. Historia de la Unión Europea En septiembre de 1946, recién terminada la Segunda Guerra Mundial, Winston Churchill, en un discurso pronunciado en la Universidad de Zurich, había hecho un llamamiento “en favor de una especie de Estados Unidos de Europa”, y en mayo de 1947, bajo su impulso, se creó el movimiento Europa Unida, que, si bien era contrario al establecimiento de órganos supranacionales, estaba a favor de la cooperación intergubernamental (Termes, 2003). El 9 de mayo de 1950, Robert Schuman, ministro francés de Asuntos Exteriores, propuso, en un discurso inspirado por Jean Monnet, la posibilidad de poner en común los recursos de carbón y de acero de Francia y de la República Federal de Alemania en una organización abierta a los demás países de Europa (Fontaine, 2003). Un año después, el 18 de abril de 1951, junto a Francia y Alemania Federal, los tres países del Benelux –Bélgica, Holanda y Luxemburgo- e Italia constituyeron en París la Comunidad Europea del Carbón y del Acero (CECA). El 25 de marzo de 1957, los seis estados de la CECA, crean, mediante el Tratado de Roma, la Comunidad Económica Europea (CEE) y la Comunidad Europea de la Energía Atómica (CEEA o EURATOM). La libre circulación de mercancías era el primer objetivo del Tratado de Roma, que no es un texto meramente económico. A medida que se profundiza en él, se aprecia su gran trascendencia política (Tamames, 1994). Entre otras cosas, dicho tratado hace referencia a la elección de los miembros del Parlamento Europeo por sufragio universal. La primera ampliación se concretó el 22 de enero de 1972 con la aceptación de los Tratados de adhesión presentados por Gran Bretaña, Irlanda, Dinamarca y Noruega en la cumbre de Jefes de estado y de gobierno en París. A continuación, a lo largo de 1972, los Tratados fueron ratificados por Irlanda y Dinamarca en referéndum, y por el Reino 1 Unido en la cámara de los Comunes. En el caso noruego, la ratificación fue rechazada en referéndum, algo que volvería a suceder en varias ocasiones a lo largo de los años siguientes. Así, el 1 de enero de 1973, la Europa de los Seis se convirtió en la Europa de los Nueve: Francia, República Federal de Alemania, Holanda, Bélgica, Luxemburgo, Italia, Gran Bretaña, Irlanda y Dinamarca. En la década de los ochenta, se llevó a cabo la ampliación de las Comunidades Europeas hacia el Sur. El 1 de enero de 1981 ingresaba Grecia, y el 1 de enero de 1986 lo hacían España y Portugal. Por otra parte, tras la caída del muro de Berlín, Alemania se reunificó después de más de 40 años, y su parte oriental se incorporó a la CEE en octubre de 1990. Los 12 países integrantes de la CEE firmaron el 7 de febrero de 1992 el Tratado de Maastricht que dio origen a la Unión Europea (UE). A mediados de los años noventa, se llevó a cabo una nueva ampliación. El 1 de enero de 1995, Austria, Suecia y Finlandia se incorporaron a la Unión. A partir de entonces, la Europa de los Quince, un espacio económico desarrollado, amplio y compacto, gracias a su prestigio político fundamentado en la práctica de la democracia parlamentaria y el respeto a los derechos humanos, quedó en condiciones de aumentar su proyección e influencia entre los países de la antigua Europa del Este: para éstos, la UE era todo un referente de estabilidad política, desarrollo económico y bienestar social (Martín y Pérez, 2003). El Consejo Europeo de Copenhague celebrado en diciembre de 2002, anunció el cierre de la primera fase de la ampliación al Este con la incorporación en el año 2004 de diez nuevos países: Hungría, Polonia, República Checa, Eslovaquia, Eslovenia, Estonia, Letonia y Lituania, además de Malta y Chipre. La adhesión de Bulgaria y Rumanía el 1 de enero de 2007, elevó a 27 el número de estados miembros y situó la población de la UE muy cercana a los 500 millones de personas (Eurostat, 2008; INE, 2008). En los países del Este protagonistas de las dos últimas ampliaciones, la población mostró una 2 tendencia descendente desde el comienzo del proceso de transición hacia una economía de mercado, debido a unas tasas netas de natalidad decrecientes y a la emigración. La última ampliación no modificó sustancialmente las principales características de la economía de la UE, ya que el peso económico de los nuevos estados miembros difería respecto del resto de estados (BCE, 2007). Si un país solicita la adhesión a la UE y su solicitud es aceptada oficialmente, se convierte en país candidato. Este es el caso actual de Turquía, Croacia y Macedonia. Para que un país candidato pueda ingresar en la UE, debe tener un sistema estable de gobierno democrático y unas instituciones que garanticen el Estado de Derecho y el respeto de los derechos humanos. También debe tener una economía de mercado eficaz y una administración capaz de aplicar las leyes y políticas de la Unión Europea (Comisión Europea, 2007). 1.2. Algunas características sociales de los países de la Unión Europea Las diferencias entre los distintos países de la UE ya eran tales cuando ésta estaba compuesta por 15 países (Puyol y Vinuesa, 1997). Estas desigualdades se mantienen e incluso se han acrecentado en la actualidad, entre los 27 países que hoy forman la UE. Coexisten espacios rurales aún atrasados, con focos avanzados de la revolución tecnológica; áreas con niveles de renta relativamente bajos, con algunos de los espacios más ricos del mundo; zonas afectadas por una profunda crisis poblacional, con áreas relativamente dinámicas desde el punto de vista demográfico; espacios socialmente muy activos, con zonas socialmente estancadas. En el caso de la distribución de ingresos, la UE está caracterizada por la presencia de clusters espaciales de regiones con niveles similares de desigualdad, mientras que hay relativamente pocos casos en los cuales una región registre un grado de dispersión de los ingresos marcadamente diferente de la media de sus vecinos (Ezcurra, Pascual y Rapún, 2007). También existen diferencias 3 entre los distintos países en el gasto destinado a protección social (entiéndase sanidad, ayudas por desempleo, jubilaciones, etc.) expresado como porcentaje del Producto Interior Bruto (PIB), existiendo por otra parte una correlación positiva entre dicho porcentaje y el gasto en protección social per cápita (Puglia, 2009). Todos estos contrastes dan lugar a la formación de un espacio europeo muy complejo, en el que los intereses de los estados, y también de las regiones, difieren considerablemente. Las condiciones de vida no son las mismas y los países del Este, protagonistas de las últimas ampliaciones, tienen características económicas y sociales distintas a las del resto de países de la UE. La equiparación de las condiciones macroeconómicas y factores sociales, juega un importante papel en la convergencia en calidad de vida dentro de los países de la Unión Europea (Welsch y Bonn, 2008). Desde mediados del siglo pasado, la esperanza de vida ha experimentado un aumento considerable, en mayor o menor medida, en los distintos países que hoy conforman la UE. El envejecimiento de la población será el cambio demográfico más importante que deba afrontar la UE en el siglo XXI. Afectará a la composición de las familias, preparativos de vida, transferencias intergeneracionales, sistema de pensiones y sistema sanitario, entre otros (Rychtarikova, 2007). Se espera que el porcentaje de personas de edad superior a 65 años sea el doble en 2050 que ahora; sin embargo, en el caso de personas de más de 80 años será el triple. Aunque la proporción de gente que llega a la edad de 100 años es todavía muy pequeña, dicha proporción crecerá también rápidamente. Asimismo, se estima que la población total de la UE pasará de 495 millones de habitantes el 1 de enero de 2008 a un máximo de 521 millones en 2035, para después disminuir progresivamente y establecerse en 506 millones en 2060 (Giannakouris, 2008). El envejecimiento de la población comenzó con un proceso conocido como Transición demográfica (Notestein, 1945), en el cual la mortalidad y la 4 fertilidad decrecían; la primera debido a los cambios sociales y económicos, y la segunda debido al coste económico que comenzó a conllevar el tener un hijo. El papel jugado por la migración internacional en el cambio de las distribuciones de edad ha sido y será, en virtud de estas estimaciones, menos importante que el descenso de la mortalidad y fertilidad. Por otra parte, la disminución de la nupcialidad ha provocado el incremento de los hijos habidos fuera del matrimonio, mientras que el divorcio, hoy en día, está menos relacionado que antes con la duración del matrimonio. Se ha observado una disminución en el número de nuevos matrimonios en los que uno o los dos cónyuges son divorciados (Puyol y Vinuesa, 1997). 1.3. Cambio climático El cambio climático es en la actualidad la mayor amenaza ambiental a la que se enfrenta el planeta. La Convención Marco de las Naciones Unidas sobre Cambio Climático (CMNUCC), antesala del Protocolo de Kioto, definió el cambio climático como un cambio de clima, atribuido directa o indirectamente a la actividad humana, que altera la composición de la atmósfera mundial, y que se suma a la variabilidad natural del clima observada durante períodos de tiempo comparables. En los últimos años, la investigación científica sobre el cambio climático se ha desarrollado considerablemente y se ha confirmado que las actividades humanas, como la quema de los carburantes fósiles, son muy probablemente las responsables del cambio climático. El calentamiento del planeta ya está teniendo muchas consecuencias medibles y para el futuro se esperan cambios costosos y de gran envergadura. Europa se calienta más rápidamente que la media mundial. La temperatura se ha elevado una media de 0,95 ºC en los últimos 100 años, y para este siglo habrá un incremento adicional de entre 2 y 6 grados centígrados (AEMA; 1998, 2004). El 5 continente europeo es muy sensible al cambio climático y las tormentas, inundaciones, sequías y otras condiciones meteorológicas extremas, serán más frecuentes. Mayor pluviosidad en el norte, pero un clima más seco en el sur, con olas de calor cada vez más habituales y deshielo de los glaciares (Nieto, 2005). Las principales reacciones de la comunidad internacional ante el fenómeno del cambio climático han surgido con la celebración de conferencias internacionales, auspiciadas por organismos internacionales. Destacan especialmente los contenidos jurídicos alcanzados en Kioto (Protocolo de Kioto) en 1997, y firmados finalmente en Nueva York el 29 de abril de 1998. El principal objetivo del Protocolo de Kioto, de conformidad con las disposiciones de la CMNUCC, es lograr la estabilización de las concentraciones de gases de efecto invernadero en la atmósfera, a un nivel que impida interferencias antropógenas peligrosas en el sistema climático. En el momento de la celebración de la conferencia en Kioto, la UE estaba compuesta por 15 países. Así, la Europa de los Quince acordó reducir sus emisiones totales de gases de efecto invernadero en un 8 % (frente a los niveles de 1990, que se utiliza como año de referencia) entre 2008 y 2012. Para alcanzar este objetivo, los quince países en cuestión llegaron a un acuerdo sobre el reparto de responsabilidades, según el cual los países menos avanzados económicamente todavía pueden seguir aumentando sus emisiones, mientras que el resto han de reducir las suyas. Diez de los países que se adhirieron posteriormente a la UE, tienen sus propios objetivos de reducción de emisiones, mientras que Chipre y Malta no tienen acordados objetivos al respecto (Comisión Europea; 2007, 2008). El efecto invernadero es un proceso natural provocado por la existencia de gases en la atmósfera que actúan permitiendo el paso de la radiación solar hacia la Tierra, pero reteniendo parte de la radiación solar reflejada por la superficie terrestre. Se produce así 6 un efecto similar al de un invernadero que suaviza las temperaturas en la superficie terrestre, permitiendo la vida sobre el planeta. En la actualidad, la emisión intensificada de gases responsables del efecto invernadero a la atmósfera, fruto de las actividades humanas, provoca un efecto invernadero antropógeno (Cancelo y Díaz, 2002). El cambio climático que padece la Tierra es una consecuencia directa de dicho efecto, puesto que los gases que lo originan, al acumularse en la atmósfera sin poder ser reabsorbidos o eliminados, provocan el calentamiento constante de la Tierra. Los expertos estiman que el dióxido de carbono (CO2) es el gas que más viene contribuyendo al conjunto de problemas y retos que plantea el cambio climático (Martín, 2005), puesto que lo hace en un 64 %. Lejos de ese porcentaje queda el metano (CH4), que incide en un 20 %, el óxido nitroso (N2O), que lo hace en un 6 %, y los componentes halógenos, tales como clorofluorocarbonos (CFC), hidrofluorocarbonos (HFC) y perfluorocarbonos (PFC), que alcanzan aproximadamente la cifra de un 10 %. Mucho se ha escrito acerca de la relación entre población y emisiones globales de dióxido de carbono, a través de factores como el consumo de energía y la producción de desperdicios y sustancias contaminantes. Diversos autores citan el tamaño de la población, la proporción per cápita de consumo de energía y materiales que contribuyen a una mayor prosperidad de los países, y el uso de las tecnologías, como los principales factores que influyen en el impacto medioambiental (Ehrlich y Holdren, 1971; MacKellar, Lutz, Prinz y Goujon, 1995; Dietz y Rosa, 1997). El incremento de la población resulta un factor determinante en las emisiones de CO2 a la atmósfera (Onozaki, 2009). Además, las variables población total y PIB están correlacionadas positivamente con las emisiones de dióxido de carbono (Shi, 2001). Basados en la relación existente entre población (e incremento de población) y emisiones globales de dióxido de carbono, algunos textos han suscitado polémica por 7 introducir en el debate medioambiental las opciones reproductivas de cada individuo y sugerir un cierto control demográfico (Ehrlich y Holdren, 1971; Harte, 2007; Murtaugh y Schlax, 2009). Por otra parte, en las últimas décadas, las emisiones globales de CO2 han crecido más rápido que la población, siendo esta relación más pronunciada para los países europeos menos desarrollados que para los países europeos más desarrollados (Martínez, Bengoechea y Morales, 2007). Además, el aumento de población en los países menos desarrollados, contribuye menos, por el momento, a las emisiones de CO2 que el consumo y aumento de población en los países más desarrollados (Bartiaux y Van Ypersele, 1993). Las proyecciones de población para los próximos años, establecen que la contribución de la población de las naciones en vías de desarrollo a la población mundial aumentará del 70 % actual a un 90 % en 2150 (Gaffin y O´Neill, 1997). 2. OBJETIVOS El primer objetivo es agrupar a los países que actualmente conforman la Unión Europea en términos de características generales sobre la población y relativas a las condiciones de vida. Realizada esta agrupación, se intentará establecer cuales de estas variables discriminan mejor entre los diferentes grupos, con objeto de predecir el comportamiento de los distintos países en función de los valores que presentan en las variables estudiadas. Asimismo, se podrán realizar predicciones acerca de en qué grupo estarían algunos países inmersos en negociaciones para entrar en la UE, o simplemente países europeos que no están ni tienen intención, por el momento, de ingresar en la UE. Dada la importancia y relevancia que un aspecto como el cambio climático adquiere en nuestros días, se plantea como objetivo examinar la relación entre las emisiones de dióxido de carbono (dadas como porcentaje del total de emisiones de la Unión Europea) y la población total de cada país. 8 Por último, se plantea el objetivo de sintetizar la información dada por las variables relativas a población y condiciones de vida, con el fin de comprobar si es posible reducir el número de variables originales, de forma que la pérdida de información sea mínima. 3. VARIABLES Y MÉTODOS 3.1. Eurostat El Sistema Estadístico Europeo es la forma de cooperación que incluye a la Oficina Estadística de las Comunidades Europeas (Eurostat), los institutos nacionales de estadística y otros organismos estadísticos nacionales, responsables, en cada uno de los países miembros, de elaborar y difundir las estadísticas europeas con arreglo a los principios del Código de buenas prácticas de las estadísticas europeas. En este marco, Eurostat se encarga de asegurar la gestión y coordinación necesarias para garantizar el suministro en tiempo útil de estadísticas de diversos campos, en apoyo de las necesidades de las políticas de la UE (De Esteban, 1994). La producción de estadísticas nacionales armonizadas, corresponde a las autoridades de los Estados miembros, mientras que la elaboración de estadísticas comunitarias, a partir de los datos suministrados principalmente por las autoridades estadísticas nacionales, corresponde a Eurostat. 3.2. Agencia Europea de Medio Ambiente La Agencia Europea de Medio Ambiente (AEMA), con sede en Copenhague, es una de las agencias especializadas de la Unión Europea. La AEMA se crea en base al Reglamento (CEE) nº 1210/90 de 7 de mayo, que entró en vigor el 30 de octubre de 1993, modificado posteriormente por el Reglamento (CE) 933/1999 del Consejo, de 29 de abril de 1999, DOCE Serie L 117 de 5 de mayo de 1999, que configura la Agencia definitivamente como un centro de referencia europeo para el medio ambiente. 9 La Agencia Europea de Medio Ambiente es el principal organismo público europeo dedicado a suministrar información ambiental a los políticos y a los ciudadanos, con el fin de apoyar el desarrollo sostenible y de contribuir a conseguir mejoras significativas y cuantificables del medio ambiente de Europa. 3.3. Variables utilizadas en este estudio Se consideran en este estudio 14 variables relativas a población y condiciones de vida, cuyos datos han sido extraídos de Eurostat. Dichos datos son referentes al año 2006. Corresponden a los 27 países que actualmente conforman la Unión Europea. Dado que el cambio climático es un tema de actualidad, se considera también la variable Emisiones de dióxido de carbono, cuyos valores vienen dados en toneladas per cápita. En este caso, los datos han sido extraídos de la Agencia Europea de Medio Ambiente y corresponden al año 2007. Volviendo a las variables relativas a población y condiciones de vida, esta es una breve descripción de las 14 variables consideradas: Población: Número de habitantes del país en cuestión. Densidad de población: Ratio de la población media de un territorio, dado el tamaño del territorio. Incremento de población: Diferencia en el tamaño de la población (en miles de habitantes) entre el final y el inicio del año estudiado. Es igual a la suma algebraica del crecimiento natural y las redes migratorias (incluyendo correcciones). Esperanza de vida: Longevidad (en años) esperada para la población general. Nacimientos fuera del matrimonio: Porcentaje de nacimientos en los que el estado civil de la madre en el momento del parto es distinto de “casada”. Matrimonios: Ratio de matrimonios por cada 1000 personas. Divorcios: Ratio de divorcios por cada 1000 personas. Desigualdad en la distribución de ingresos: La ratio de ingresos totales recibidos por 10 el 20 % de la población con los ingresos más altos sobre los recibidos por el 20 % de la población con los ingresos más bajos. Riesgo de pobreza en la población antes de recibir transferencias sociales (%). Riesgo de pobreza en la población después de recibir transferencias sociales (%). Porcentaje del PIB dedicado a gasto social: Porcentaje del PIB destinado a protección social. Gasto social per cápita: Gasto per cápita destinado a protección social (dado en miles de euros). Acceso a Internet: Porcentaje de hogares con acceso a Internet. Renta per cápita (en miles de euros). 3.4. Análisis Multivariante Una de las razones de la dificultad de definir el análisis multivariante es que el término multivariante no se usa de la misma forma en la literatura. En un sentido amplio, el análisis multivariante se refiere a todas las técnicas estadísticas que simultáneamente analizan medidas múltiples recogidas sobre individuos, objetos, etc. Para algunos investigadores, podrían considerarse multivariantes todos los análisis simultáneos de más de dos variables (Tabachnick y Fidell, 1996). Otros autores reservan el término para situaciones en las que el conjunto de variables sigue una distribución normal multivariante (Anderson, 1984) y a veces se añade la condición de que todas las variables deben ser aleatorias e interrelacionadas, de modo que sus efectos no pueden estudiarse por separado (Bernstein, 1987). Puede definirse el análisis multivariante simplemente como conjunto de métodos que analizan las relaciones entre un número razonablemente amplio de medidas (variables), tomadas sobre cada objeto o unidad de análisis, en una o más muestras simultáneamente (Martínez, 1999). En esta definición, el punto importante es que las técnicas multivariantes tratan las relaciones simultáneas 11 entre las variables. Las técnicas multivariantes utilizadas en este estudio, han sido: Análisis Cluster, Análisis Discriminante, Análisis de Correspondencias, Análisis Factorial y Análisis de Componentes Principales. Dichas técnicas serán explicadas brevemente a continuación. 3.4.1. Análisis Cluster El análisis cluster es la denominación de un grupo de técnicas multivariantes cuyo principal propósito es agrupar objetos basándose en las características que poseen. El análisis cluster clasifica objetos o individuos, basándose en las características que éstos poseen. Los conglomerados de objetos resultantes deberían mostrar un alto grado de homogeneidad interna (dentro del conglomerado) y un alto grado de heterogeneidad externa (entre conglomerados). Las variables a las que se aplica el análisis han de ser de tipo cuantitativo, teniendo en cuenta además que los resultados pueden verse muy afectados por la inclusión de variables inadecuadas e irrelevantes, por lo que las variables serán seleccionadas dentro del contexto de una teoría que apoye la investigación. Una vez seleccionadas las variables, el investigador debe plantearse tres cuestiones que pueden incidir en los resultados finales (Martínez, 1999): 1) presencia de observaciones aisladas en los datos y qué hacer con ellas; 2) transformaciones sobre las variables, especialmente su posible estandarización o ponderación; 3) elección de la medida de similaridad. La similaridad entre objetos es el punto de partida de cualquier clasificación en el análisis cluster, ya que es la que proporciona las matrices de similaridades. Los objetos son evaluados respecto de una serie de características o dimensiones, y éstas deben ser combinadas en una medida de similaridad calculada para todos los pares de objetos. La similaridad entre los objetos puede evaluarse según una gran variedad de procedimientos: medidas correlacionales, medidas de distancia y medidas de asociación. 12 La distancia euclídea es una de las medidas de similaridad preferidas y más utilizadas por los investigadores (Kendall, 1980). Una vez calculadas las matrices de similaridad, comienza el proceso de partición o formación de grupos. En la práctica, hay dos grandes grupos de procedimientos: los métodos jerárquicos, que son aquellos, que para formar un cluster nuevo, unen o separan alguno ya existente para dar origen a otros dos, de forma que se maximice una similaridad o se minimice una distancia; por otro lado, están los métodos no jerárquicos, donde los individuos se clasifican en k grupos, estudiando todas las particiones de individuos en esos k grupos y eligiendo la mejor partición. La principal ventaja de los métodos jerárquicos es que se puede representar el problema en forma de árbol o dendograma, donde se observa muy bien la solución final. Hay un amplio elenco de métodos que difieren en cómo establecen las distancias entre los conglomerados (linkaje simple, linkaje completo, agrupación de medias, método de Ward, método de McQuitty,…). En cuanto a la valoración del ajuste, en el caso de los procedimientos jerárquicos, el método más empleado es el coeficiente cofenético, que determina el ajuste entre el dendograma resultante y el patrón de similaridades entre los datos. Este coeficiente es la correlación entre los n⋅(n-1) / 2 elementos de la parte superior de la matriz de proximidades o distancias frente a la matriz cofenética C, cuyos elementos cij se definen como aquellos que determinan la proximidad entre los elementos i y j cuando estos se unen en el mismo cluster. De esta manera, el método con un coeficiente más elevado será el que presente menor distorsión en las relaciones originales existentes en los elementos. El análisis cluster puede caracterizarse como descriptivo, ateórico y no inferencial. No tiene bases estadísticas sobre las cuales deducir inferencias estadísticas para una población a partir de una muestra, y se utiliza fundamentalmente como una técnica 13 exploratoria (Hair et al, 1995). Las soluciones no son únicas, en la medida en que la pertenencia al conglomerado para cualquier número de soluciones depende de muchos elementos del procedimiento, y se pueden obtener muchas soluciones diferentes variando uno o más de estos elementos. Los requisitos de normalidad y homocedasticidad, importantes en otras técnicas, no se aplican en el análisis cluster, aunque son importantes otros aspectos como la representatividad de la muestra y la presencia de multicolinealidad. 3.4.2. Análisis Discriminante El análisis discriminante es una técnica estadística que permite analizar las diferencias entre dos o más grupos con respecto a un conjunto de variables simultáneamente, y asignar o clasificar individuos en el grupo que les sea más próximo (Klecka, 1982). Así pues, se trata de analizar cuáles son las variables que contribuyen en mayor grado a discriminar a los sujetos en los diferentes grupos establecidos a priori. Para ello, estas variables que mejor discriminan se reducen a variables canónicas, que no son otra cosa sino una combinación lineal de las variables independientes originales (Visauta, 1998). Esta combinación lineal es lo que se conoce como función discriminante, donde la variable dependiente es la pertenencia a uno u otro grupo. Dados k grupos, existen k-1 funciones discriminantes, y para que sean óptimas han de proporcionar una regla de clasificación que minimice la probabilidad de cometer errores. Las hipótesis para llevar a cabo este análisis (Rivas, Rius y Martínez, 1990) son: 1) la existencia de dos o más grupos que difieran sobre varias variables, y que éstas estén dadas en escala de intervalo o razón; 2) la clasificación a priori de los individuos ha de ser mutuamente excluyente; 3) cada grupo debe ser extraído de una población que se distribuye según una normal multivariante; 4) las matrices de varianza-covarianza de las distintas poblaciones de las que provienen los grupos, deben ser iguales. La condición 14 de normalidad se puede omitir, dada la robustez de la técnica del análisis discriminante, si no se rechaza la hipótesis de igualdad de matrices de varianza-covarianza poblacionales. Dicha hipótesis se contrasta mediante el test M de Box1. El problema es que, cuando el tamaño de muestra es pequeño, este test no se puede realizar. En esas circunstancias, se pueden simplemente observar las desviaciones típicas y estudiar que son relativamente parecidas. Por otra parte, la multicolinealidad y la singularidad son dos características que, en caso de aparecer en las matrices de correlaciones, pueden provocar que los resultados a los que se llega en ésta y otras técnicas de análisis multivariante no sean válidos (Gil, García y Rodríguez, 2001). La multicolinealidad ocurre cuando dos variables de la matriz de correlaciones presentan una correlación muy fuerte, cercana a la unidad. Mientras, la singularidad supondría que las puntuaciones alcanzadas en una variable fuesen aproximadamente una combinación lineal de otras. Si hay multicolinealidad o singularidad, el determinante de la matriz de correlaciones estará próximo a cero, con lo que la matriz inversa presentará valores muy inestables o imposibles de obtener. En el caso del análisis discriminante, la inversión de matrices se requiere en el cálculo de los coeficientes para la función discriminante. Las funciones discriminantes se expresan por medio de una ecuación como la siguiente, Z = a1X1 + a2X2 +…+ apXp , donde: Z = puntuación discriminante aj = peso discriminante para la variable j-ésima Xj = variable independiente o predictora 1 El test M de Box es una generalización del test de Bartlett para la comprobación de la homogeneidad de varianzas univariadas; se basa en los determinantes de las matrices de varianza-covarianza para cada grupo. 15 Promediando las puntuaciones discriminantes para todos los individuos dentro de un grupo particular, se obtiene una media del grupo, denominada centroide. Los centroides indican la posición más típica de los individuos de un grupo particular, y una comparación de los centroides de los grupos muestra su alejamiento o separación de la función discriminante. El contraste de significación de la función discriminante es una medida generalizada de la distancia entre los centroides de los grupos, y se calcula comparando las distribuciones de las puntuaciones discriminantes para dos o más grupos. Uno de los contrastes de la significación estadística de las funciones discriminantes más utilizados, es el de la lambda de Wilks. El coeficiente de correlación canónica, Γi, es una medida de asociación que indica el grado de relación entre los grupos y la función discriminante en cuestión. Dicho coeficiente oscila entre 0 y 1, y, cuanto mayor es el valor, mejor es la asociación. Sea αi el autovalor asociado, α Γi = i 1+ αi 1/ 2 . Para la validación de los resultados, se usa un procedimiento equivalente al de la R2 en regresión, que es la ratio de aciertos. Esto es, el porcentaje de individuos correctamente clasificados; una ratio de aciertos elevada es indicativa de que el análisis discriminante resulta adecuado. Esta ratio se obtiene a partir de la matriz de clasificación, que presenta, para los casos observados en un grupo, cuántos de ellos se esperaban en un grupo y cuántos en los restantes. 3.4.3. Análisis de Correspondencias El análisis de correspondencias es una técnica de interdependencia que facilita la reducción dimensional de una clasificación de objetos sobre un conjunto de atributos, y 16 el mapa perceptual de objetos relativos a estos atributos. El análisis de correspondencias difiere de otras técnicas de interdependencia en su capacidad para acomodar tanto datos no métricos como relaciones no lineales (Hair et al., 1995). Sean I y J dos conjuntos finitos. Su producto cartesiano es I x J. Definir una correspondencia entre I y J consiste en asociar a cada elemento (i, j) de I x J un número no negativo K (i, j). Así, se representa la correspondencia por medio de una tabla rectangular. Si todos los valores K (i, j) son enteros, se trata de una correspondencia estadística, pues los números indican cuántas veces se presenta el elemento (i, j). Estas tablas se conocen como tablas de contingencia. En su forma básica, el análisis de correspondencias examina las relaciones entre categorías de datos nominales o perfiles, mediante la medida de asociación de la chi- cuadrado. Usando la chi-cuadrado como distancia, la matriz se centra tanto por filas como por columnas, pues lo más habitual es realizar el análisis de cada nube de puntos respecto del centro de gravedad (Joaristi y Lizasoain, 2000). La formulación de esta distancia es similar a la distancia euclídea entre puntos de un determinado espacio, con la diferencia de que en este caso se divide cada cuadrado de la diferencia entre coordenadas por su correspondiente elemento del perfil medio. El análisis de correspondencias sólo requiere que los datos representen las respuestas a una serie de preguntas, y que éstas estén organizadas en categorías. Dependiendo de si existen dos o más variables, el análisis será simple o múltiple. El análisis de correspondencias calculará perfiles, inercias, contribuciones, etc., de las diversas filas y/o columnas de la tabla, y además permitirá analizar la relación entre las variables de un modo gráfico en un espacio pluridimensional, de modo que, previo cálculo por filas y columnas de las puntuaciones de la tabla, las diversas categorías de las variables 17 estarán representadas en el gráfico más próximas o alejadas en las diversas dimensiones, en función de su grado de similitud o diferencias. El estadístico chi-cuadrado (χ2) es una medida global de las diferencias entre las frecuencias observadas y las frecuencias esperadas de una tabla de contingencia. Las frecuencias esperadas se calculan mediante la hipótesis de homogeneidad de los perfiles fila (o de los perfiles columna). La inercia total de una tabla de contingencia es igual al estadístico χ2 dividido por el total de la tabla. Geométricamente, la inercia mide como se alejan los perfiles fila (o perfiles columna) de su perfil medio. Se puede considerar que el perfil medio simboliza la hipótesis de homogeneidad de los perfiles (Greenacre, 2008). La inercia será alta cuando los perfiles fila (o columna) presenten grandes desviaciones con relación a su media, y será baja cuando éstos se hallen cerca de la media. Si todos los perfiles fueran idénticos, y por tanto se hallaran todos en el mismo punto (su media), todas las distancias chi-cuadrado serían cero, y también lo sería la inercia total. Sean I el número de filas y J el número de columnas de la tabla (I, J ≥ 2), el número máximo de dimensiones será el mínimo de los valores I−1 y J−1 (Juaristi y Lizasoain, 2000). Respecto a la proporción de inercia que recoge cada una de estas dimensiones, la primera reflejará la mayor proporción de inercia de los datos, la segunda la siguiente, y así sucesivamente hasta completar el 100 % (Visauta, 1998). El análisis de correspondencias también tiene desventajas o limitaciones (Hair et al., 1995). La técnica es descriptiva y no del todo apropiada para el contraste de hipótesis. Por otra parte, como ocurre con muchos métodos de reducción de dimensionalidad, no cuenta con un método para determinar concluyentemente el número de dimensiones apropiado. En cualquier caso, el investigador no debe perder de vista la interpretabilidad de la solución obtenida. 18 En esencia, el análisis de correspondencias es un tipo especial de análisis de componentes principales, pero realizado sobre una tabla de contingencia y usando una distancia euclídea ponderada, como es la chi-cuadrado, cuya principal propiedad es la posibilidad de una representación simultánea de las variables y las poblaciones (Benzécri, 1976). 3.4.4. Análisis de Componentes Principales El Análisis de Componentes Principales es una técnica estadística dirigida a reducir la dimensión (número de variables), con pérdida de información mínima y controlada por el investigador. Ante un conjunto de datos de muchas variables, el objetivo será reducirlas a un menor número, perdiendo la menor cantidad de información posible. Puede definirse también como una técnica descriptiva destinada a estudiar la dependencia o estructura correlacional de muestras multivariantes (Morrison, 1976). Supóngase que se tienen observaciones de p variables, X1, X2,…, Xp en n individuos. Se intenta entonces simplificar la situación, observando si es posible encontrar nuevas variables, ξ1, ξ2,…, ξp, las cuales sean respectivamente funciones lineales de X1, X2,…, Xp, y estén incorreladas entre sí. De hecho, se buscan p2 constantes lij (i, j = 1, 2,…, p) tales que ξ = ∑l ⋅ X , p i j =1 ij j con Var (ξ1) ≥ Var (ξ2) ≥ … ≥ Var (ξp) (Kendall, 1980). Las nuevas funciones son conocidas como componentes principales o factores. En particular, si las variables originales siguen una distribución normal, las nuevas variables ξi serían, además de incorreladas, independientes. Se pretende, pues, que la primera componente recoja la mayor proporción posible de la variabilidad original, que la segunda recoja la máxima variabilidad posible no recogida por la primera, y así sucesivamente. Del total de componentes, se elegirán aquellas que 19 expliquen el porcentaje de variabilidad que se considere suficiente. Las componentes principales conservan la variabilidad total inicial, es decir, la suma de las varianzas de las componentes principales es igual a la suma de las varianzas de las variables originales. Un análisis de componentes principales carece de sentido cuando las variables originales están incorreladas, pues, en ese caso, ellas mismas son las componentes principales. Por el contrario, el hecho de que las correlaciones entre las variables originales sean elevadas, será de gran utilidad, ya que esto es indicativo de que existe información redundante y, por tanto, pocos factores explicarán gran parte de la variabilidad total. Cuando existen altas correlaciones positivas entre las variables, la primera componente principal tiene todas sus coordenadas del mismo signo y se interpreta como un promedio ponderado de las variables originales, o un factor conjunto de tamaño. Las sucesivas componentes, con coordenadas factoriales de ambos signos, se interpretan como factores de forma, contraponiendo el grupo de variables originales con coeficientes factoriales positivos con el de variables con coeficientes negativos. La interpretación de las componentes se facilita suponiendo nulos los coeficientes factoriales muy pequeños, y redondeando los grandes para futuros usos. La elección del número a partir del cual pueden considerarse nulos los coeficientes, está en relación con el resto de éstos y (como la elección del análisis, el número de componentes y su interpretación) depende mucho del conocimiento del problema y la experiencia del investigador. Un aspecto clave en el análisis de componentes principales es la interpretación de los factores o componentes, ya que ésta no viene dada a priori por la teoría, sino que debe deducirse tras observar las relaciones de los factores con las variables iniciales (habrá, 20 pues, que estudiar tanto el signo como la magnitud de las correlaciones). Esto no es siempre fácil, y será de gran importancia el conocimiento que el experto tenga sobre la materia de investigación. 3.4.5. Análisis Factorial En 1904, Charles Spearman publicaba un artículo2 donde trabajaba con las puntuaciones obtenidas por 33 estudiantes en distintos exámenes, observando ciertos efectos sistemáticos en la matriz de correlación entre puntuaciones. Este artículo puede ser considerado el origen del análisis factorial (Kendall, 1980). El análisis factorial es un nombre genérico que se da a una clase de métodos estadísticos multivariantes cuyo propósito principal es definir la estructura subyacente en una matriz de datos. Generalmente hablando, aborda el problema de cómo analizar la estructura de las interrelaciones (correlaciones) entre un gran número de variables, con la definición de una serie de dimensiones subyacentes comunes, conocidas como factores. El análisis factorial se suele utilizar en la reducción de los datos para identificar un pequeño número de factores, que expliquen la mayor parte de la varianza observada de un número mayor de variables manifiestas. Las técnicas analíticas de factores pueden lograr sus propósitos desde una perspectiva exploratoria o confirmatoria. Existe una discusión continuada acerca del papel adecuado del análisis factorial (Hair et al. 1995). Muchos investigadores lo consideran meramente exploratorio; desde esta perspectiva, las técnicas de análisis factorial extraen lo que proporcionan los datos, y no tienen restricciones sobre la estimación de los factores o el número de factores a retener. Para muchas aplicaciones, resulta adecuado este uso del análisis factorial. No obstante, hay situaciones en las que el investigador tiene unos 2 El artículo en cuestión es “General Intelligence”, objectively determined and measured , originalmente publicado en American Journal of Psychology 15 (1904), 201-293, y disponible en http://psychclassics.yorku.ca/Spearman/ 21 pensamientos preconcebidos sobre la estructura real de los datos, que se basan en un apoyo teórico o en investigaciones previas; en estos casos, se requiere un análisis factorial desde un punto de vista confirmatorio. Es por ello que el análisis factorial puede ser exploratorio o confirmatorio. En este estudio, el enfoque ha sido exploratorio, por lo que en todo momento se hará referencia al análisis factorial desde un punto de vista exploratorio. El análisis factorial está relacionado con el análisis de componentes principales, pero entre ambas técnicas existen notables diferencias. La primera es que la finalidad de las componentes principales es simplificar la estructura de los datos, sin obedecer a un modelo fijado “a priori”, para poder explicar, en pocas componentes, la mayor parte de la información que contienen las variables; por su parte, el análisis factorial pretende estudiar relaciones de dependencia entre las variables, expresadas a través de un modelo de factores comunes y únicos (Cuadras, 1991). Además, mientras el análisis de componentes principales es una técnica descriptiva, apoyada únicamente en las propiedades matemáticas de las matrices de covarianza o de correlación, el análisis factorial presupone un modelo estadístico al que deben adaptarse los datos. Dentro de las hipótesis previas, la primera de ellas sería la normalidad, aunque ésta sólo es necesaria si se realizan pruebas estadísticas de significación. Es deseable que exista un cierto grado de multicolinealidad, ya que el objetivo es identificar variables relacionadas. El análisis factorial debe tener suficientes correlaciones altas para poder aplicarse. Si no hay un número sustancial de correlaciones moderadas (por ejemplo, coeficiente de correlación de Pearson r > 0.30), entonces probablemente sea inadecuado realizar este análisis. Sean zi (i = 1,…, p) p variables independientes, las cuales siguen una distribución normal multivariante (esto implica que cada par de variables siga una distribución 22 normal bivariante). Se asume que las variables están estandarizadas y se denota la matriz de correlación poblacional por Σ. Esta matriz es de orden y rango p. Supóngase ahora que hay restricciones en los coeficientes de correlación de Σ tales que, mediante ajuste de los elementos de su diagonal, su rango puede ser reducido de p a k, que sería el número de variables, o hipotéticas dimensiones de variabilidad, que representan los factores comunes de las p variables iniciales. El modelo factorial puede ser expresado en términos algebraicos por la ecuación lineal (Maxwell, 1977) z i = (λi1 ⋅ f 1 + ... + λik ⋅ f k ) + ei , que establece que cada variable zi es una suma ponderada de k factores, más una variable residual específica para cada zi. Las variables residuales se toman de forma que estén incorreladas entre sí, mientras que los factores se toman con media cero y varianza unidad, e incorrelados entre sí. La validez de los resultados y la adecuación del análisis, vienen condicionadas por obtener valores significativos del índice de Kaiser-Meyer-Olkin (KMO3) y el test de esfericidad de Bartlett4, que se obtienen a partir de la matriz de correlaciones. Los diferentes métodos de extracción factorial (tales como, por ejemplo, Componentes Principales, Máxima verosimilitud o factorización Alfa) intentan determinar el número mínimo de factores comunes capaces de reproducir la varianza observada en la matriz de correlaciones inicial. Una comparación entre ellos puede hacerse en función del enfoque utilizado en la extracción, el método de extracción de las comunalidades o el hecho de que las puntuaciones factoriales sean estimadas o calculadas (García, Gil y Rodríguez, 2000). 3 El índice KMO es una medida de la adecuación muestral. Si la suma de los coeficientes de correlación parciales al cuadrado entre todos los pares de variables es pequeña, comparada con la suma de los coeficientes de correlación al cuadrado, la medida KMO se aproxima a la unidad. Esta medida oscila entre 0 y 1; valores inferiores a 0.6 cuestionan el empleo del modelo factorial. 4 La prueba de Bartlett contrasta si la matriz de correlaciones es la matriz identidad como hipótesis nula, es decir, que las variables estén incorreladas; en caso de aceptarse esta hipótesis, el modelo factorial sería inadecuado. 23 Utilizar algún procedimiento de rotación responde a la idea de hacer más fácil la interpretación de los valores que presenta la matriz factorial tras la extracción. La rotación consiste en girar los ejes factoriales. La solución inicial extrae los factores según su importancia, y los siguientes factores van explicando progresivamente menor porcentaje de varianza. Con la rotación se distribuye la varianza en otros factores para lograr un patrón de factores más simple y más significativo. Existen muchos métodos de rotación y de la elección de uno u otro dependerá de la solución. Un método frecuentemente utilizado es Varimax (Kaiser, 1958), basado en el hecho de que si se logra aumentar la varianza de las cargas factoriales al cuadrado de cada factor, consiguiendo que algunas de sus cargas factoriales tiendan a acercarse a uno mientras otras se acerquen a cero, lo que se obtiene es una pertenencia más clara e inteligible de cada variable a ese factor. La rotación Varimax es ortogonal, lo que significa que los factores permanecen incorrelados con el proceso de rotación. Hay ocasiones en que los factores no necesitan estar incorrelados e incluso pueden estar conceptualmente ligados, lo que requiere una correlación entre los factores. Puede ser adecuado entonces el uso de una rotación oblicua (Hair et al., 1995). 3.5. Software empleado para realizar el análisis de los datos Para realizar los análisis previstos en este estudio, se han utilizado la versión 16.0 del programa SPSS (Statistical Package for the Social Sciences), la versión 5.1 Plus del StatGraphics y el programa de distribución libre R, en su versión 2. 8. 0. 4. RESULTADOS 4.1. Análisis Cluster Para llevar a cabo la agrupación de los países de la UE-27 en función de los valores que presentaban en las variables referentes a población y condiciones de vida, se realizó un análisis cluster. Se tipificaron en primer lugar las variables, con el objetivo de que 24 estuvieran todas medidas en la misma escala. Se comprobó que no había observaciones anómalas debido a la manipulación y tratamiento de los datos, y que, en el caso de haberlas, correspondían a observaciones reales, como era el caso de Alemania en la variable Población. Se utilizó como medida de asociación la distancia euclídea y se emplearon métodos jerárquicos, representándose la solución final en forma de dendograma. El método se escogió en función del coeficiente cofenético (Tabla 1). A la vista de los resultados obtenidos, el método ideal era el de agrupación de medias. Utilizando el método de agrupación de medias y la distancia euclídea, se observó que Malta constituía un cluster aislado y también se apreció la agrupación de los países que conformaban la antigua Europa de los Quince, con la excepción de Grecia y Portugal (Figura 1). Se optó por una solución de tres grupos, cuya composición fue la siguiente: Grupo 1: Bélgica, Austria, Dinamarca, Finlandia, Suecia, Holanda, Alemania, Luxemburgo, Irlanda, España, Italia, Francia y Reino Unido. Grupo 2: Bulgaria, República Checa, Eslovaquia, Eslovenia, Estonia, Letonia, Lituania, Hungría, Portugal, Polonia, Rumanía, Grecia y Chipre. Grupo 3: Malta. Método empleado Coeficiente cofenético Linkaje simple 0,62087 Linkaje completo 0,66405 Método de Ward 0,59293 Agrupación de medias 0,75951 Método de Mc Quitty 0,71771 Agrupación de medianas 0,48255 Agrupación de centroides 0,58925 Tabla 1: Coeficiente cofenético asociado a distintos métodos jerárquicos. 25 Figura 1: Dendograma asociado al método de agrupación de medias, empleando la distancia euclídea. Se pueden observar dos grupos diferenciados, excluyendo a Malta. 4.2. Análisis Discriminante Se trató, en segundo lugar, de determinar en qué variables, de las 14 relativas a población y condiciones de vida, se encontraban mayores diferencias entre los países de la Unión Europea, en función del cluster al que pertenecían. Para ello, se llevó a cabo un análisis discriminante, considerando los grupos 1 y 2 como la variable dependiente. Por razones de tamaño muestral, no tenía sentido considerar el cluster exclusivamente compuesto por Malta. Se encontraron diferencias significativas, a un nivel de confianza del 95 %, entre las medias de ambos grupos en las variables Población (F (1; 24) = 4,842; p = 0,038), Densidad de población (F (1; 24) = 4,595; p = 0,042), Incremento de población (F (1; 24) = 6,268; p = 0,019), Esperanza de vida (F (1; 24) = 34,438; p < 0,001), Acceso a Internet (F (1; 24) = 27,393; p < 0,001), Desigualdad de ingresos (F (1; 24) = 4,476; p = 0,045), Porcentaje del PIB dedicado a gasto social (F (1; 24) = 25,027; p < 0,001), Gasto social per cápita (F (1; 24) = 59,109; p < 0,001) y Renta per cápita (F (1; 24) = 26 40,950; p < 0,001). En todos los casos, las diferencias fueron favorables a los países que componían el primer grupo. En el caso de las variables Población, Densidad de población e Incremento de población, los países de ese primer grupo estaban más poblados y experimentaban un mayor incremento en la población al cabo del año estudiado. Estas 9 variables eran, por tanto, las realmente importantes a la hora de discriminar si un estado estaba dentro de uno u otro grupo. Especialmente importantes eran, a la vista de la significación, la Esperanza de vida, el Acceso a Internet, el Porcentaje del PIB dedicado a gasto social, el Gasto social per cápita y la Renta per cápita, por lo que se partió de estas 5 variables para realizar el análisis discriminante. Dado que el test M de Box era de difícil aplicación en este caso, debido al tamaño muestral, convenía fijarse en la homocedasticidad de las varianzas. Mediante la prueba de Levéne, se confirmó que, salvo la Esperanza de vida, en las otras 4 variables se verificaba la hipótesis de homocedasticidad entre ambos grupos. Teniendo en cuenta la relación teórica entre el Porcentaje del PIB dedicado a gasto social y el Gasto social per cápita, y que además el Gasto social per cápita presentaba en este caso una alta correlación con la Renta per cápita (r = 0,943), se optó por realizar un análisis discriminante considerando como variables independientes el Porcentaje de hogares con acceso a Internet y el Gasto social per cápita. Dada la correlación moderada entre ambas variables (r = 0,772), no hubo problemas de multicolinealidad ni singularidad. Al ser sólo dos grupos, la única función discriminante resultante fue D = -3,684 + 0,021⋅X1+0,489⋅X2, donde X1 = Porcentaje de hogares con acceso a Internet X2 = Gasto social per cápita (en miles de euros) 27 La correlación canónica fue alta, Γ = 0,851, y el valor de la lambda de Wilks próximo a cero (lambda = 0,276, p < 0,001), lo que indicaba que la función era útil para discriminar ambos grupos. De hecho, clasificó correctamente al 96,3 % (Tabla 2) de los países cuya pertenencia a un grupo u otro era conocida, por lo que el procedimiento resultó adecuado. Sólo cometió un error, España, país al que clasificaba en el segundo grupo, cuando realmente pertenecía al primer grupo. Otra de las utilidades de este análisis discriminante era el hecho de poder predecir a que grupo pertenecería un país europeo que, en el momento del análisis, no formase parte de la UE. En este sentido, se tenían datos de Acceso a Internet y Gasto social per cápita de los siguientes países: Croacia, Turquía, Macedonia, Islandia, Suiza y Noruega. Croacia, Turquía y Macedonia fueron clasificados dentro del grupo 2, el compuesto por los países incorporados a partir de 2004, además de Grecia y Portugal. Por el contrario, Islandia, Suiza y Noruega, estarían, con los datos que presentaban, en el grupo 1. Malta fue pronosticada dentro del grupo 2. País Grupo real Probabilidad de pertenencia al grupo 2 0,010 Grupo pronosticado P. D. 1 Probabilidad de pertenencia al grupo 1 0,990 Alemania 1 1,493 Austria 1 0,993 0,007 1 1,577 Bélgica 1 0,994 0,006 1 1,617 Bulgaria 2 0,000 1 2 -2,694 Chipre 2 0,049 0,951 2 -0,953 Dinamarca 1 0,999 0,001 1 2,281 Eslovaquia 2 0,002 0,998 2 -1,949 Eslovenia 2 0,346 0,654 2 -0,205 España 1 0,258 0,742 2 -0,340 28 Estonia 2 0,004 0,996 2 -1,749 Finlandia 1 0,977 0,023 1 1,211 Francia 1 0,976 0,024 1 1,187 Grecia 2 0,175 0,825 2 -0,499 Holanda 1 1 0,000 1 2,447 Hungría 2 0,015 0,985 2 -1,348 Irlanda 1 0,806 0,194 1 0,458 Italia 1 0,732 0,268 1 0,323 Letonia 2 0,002 0,998 2 -2,044 Lituania 2 0,002 0,998 2 -2,082 Luxemburgo 1 1 0,000 1 4,368 Malta - 0,048 0,952 2 -0,957 Polonia 2 0,004 0,996 2 -1,767 Portugal 2 0,083 0,917 2 -0,772 Reino Unido 1 0,981 0,019 1 1,264 República Checa 2 0,013 0,987 2 -1,393 Rumanía 2 0,000 1 2 -2,765 Suecia 1 0,999 0,001 1 2,335 Croacia - 0,019 0,981 2 -1,266 Islandia - 0,980 0,020 1 1,257 Macedonia - 0,000 1 2 -2,837 Noruega - 1 0,000 1 2,608 Suiza - 0,997 0,003 1 1,830 Turquía - 0,000 1 2 -2,765 - : Países desagrupados. P.D.: Puntuación discriminante Tabla 2: Clasificación de los respectivos países y probabilidad de que pertenezca a uno u otro grupo basada en la predicción. 29 4.3. Análisis de Correspondencias Mediante el coeficiente de correlación de Pearson, se observó que existía una fuerte relación lineal entre las emisiones de CO2 de un país (dadas en porcentaje del total de emisiones de la UE) y su población total (r = 0,976; p < 0,001). Se realizó un análisis de correspondencias considerando categóricas ambas variables. En el caso de la variable Emisiones de dióxido de carbono, se consideraron tres categorías: países que emitían más del 3 % de las emisiones totales de la UE (E1), países que emitían entre un 1 y un 3 % (E2), y países que emitían menos del 1 % de dichas emisiones (E3). Mientras, dentro de la variable Población se consideraron tres grupos: países con más de 15 millones de habitantes (P1), entre 5 y 15 millones (P2), y menos de 5 millones de habitantes (P3). Se clasificaron así los 27 países que forman la UE en una tabla de contingencia de dimensiones 3 x 3 (Tabla 3). Se eligió para realizar este análisis la distancia chi-cuadrado y el método de normalización simétrico. Dado que 3 era el número de categorías de cada variable, el número de ejes o dimensiones apropiado fue igual a 2. Población Emisiones de CO2 (% del total de emisiones de la UE) P1 P2 P3 E1 7 1 0 8 E2 1 9 1 11 E3 0 1 7 8 8 11 8 27 Tabla 3: Tabla de contingencia de los 27 países de la UE, en función de población y emisiones de CO2. Se observó, entre otras cosas, que 7 de los 8 países más poblados de la UE estaban entre los países que más contaminaban en términos totales. Los dos ejes o dimensiones resultantes explicaron un total de inercia de 1,246. De esta inercia, 0,766 correspondió al primer eje. A partir de aquí se obtuvo que el primer eje explicaba un 61,4 % de la 30 variabilidad total (Tabla 4). Existió una gran asociación entre las dos variables categóricas consideradas (χ2 (4) = 33,645; p < 0,001), algo que resultaba obvio observando la acumulación de frecuencias en la diagonal de la tabla de contingencia. Por ello, se aceptó, a un nivel de confianza muy próximo al 100 %, la hipótesis de dependencia entre ambas variables (Figura 2). χ2 (4 g.l.) Dimensión Valor propio Inercia 1 0,875 0,766 Inercia explicada 0,614 2 0,693 0,481 0,386 Total 1,246 33,645 (p<0,001) 1,000 Tabla 4: Inercia de las dimensiones. En el caso de la variable Porcentaje de emisiones, del total de inercia (1,246), las dos categorías extremas (E1 y E3) fueron las que más aportaban: 0,481 cada una. La situación fue idéntica, conceptualmente, en el caso de la variable Población. Por otra parte, y esto sucedía también en ambas variables por igual, las categorías extremas eran los valores más importantes para la orientación del primer eje, mientras que la categoría intermedia lo era para el segundo. Figura 2: Correspondencias entre las 3 categorías de emisiones de CO2 (dadas en porcentaje del total de la UE) y la población del país emisor (expresada en tres categorías diferentes). 31 4.4. Análisis de Componentes Principales Se realizó un análisis de componentes principales sobre las 14 variables originales referentes a población y condiciones de vida. Mediante el test de esfericidad de Bartlett (χ2 (91) = 288,992; p < 0,001), se rechazó la hipótesis de que la matriz de correlaciones fuese igual a la identidad, y por tanto que las variables estuvieran incorreladas. Dado que las variables estaban correlacionadas entre sí, tenía sentido realizar un análisis de componentes principales. Se eligió un número de componentes que recogiese un porcentaje de variabilidad suficiente. En este caso, el criterio utilizado fue escoger tantas componentes como autovalores mayores que 1 tuviese asociados la matriz de correlaciones. Como se puede observar en el gráfico de sedimentación asociado (Figura 3), la matriz de correlaciones presentó cuatro autovalores mayores que la unidad, lo que sugirió que cuatro sería el número adecuado de componentes para este análisis. El primer autovalor fue el mayor, y el que más contribuía a la explicación de las variables originales: concretamente, explicó un 34,37 % de la variabilidad total. El segundo y el tercero explicaron un porcentaje similar (16,14 % y 14,79 %, respectivamente), mientras el cuarto explicó un 10,11 %. Globalmente, estas cuatro componentes principales explicaron un 75,40 % de la variabilidad total de los datos originales. 5 Autovalor 4 3 2 1 0 1 14 Componente Figura 3: Gráfico de sedimentación asociado al análisis de componentes principales realizado. 32 Debido a que las correlaciones entre las variables fueron por lo general moderadamente altas, pero no excesivamente altas, la primera componente no resultó ser una componente de tamaño, puesto que no todos los coeficientes de la primera componente tenían el mismo signo (Tabla 5). Esta componente, la más importante, contrapuso las variables Matrimonios, Divorcios, Desigualdad de Ingresos y Riesgo de Pobreza después de transferencias sociales frente al resto de variables estudiadas. La segunda componente contraponía variables que representaban cambios sociales (como son Niños nacidos fuera del matrimonio, Divorcios o Acceso a Internet) y la Densidad de Población, frente al resto de variables. La tercera componente, por su parte, contrapuso la Esperanza de vida y las variables demográficas frente a las diez variables restantes. Variables Población Componente 1 0,1285 Componente 2 0,3959 Componente 3 0,0667 Componente 4 0,3549 Dens_Pobl 0,0846 -0,1036 0,4809 -0,2645 Increm_Pobl 0,1217 0,4437 0,0786 0,3385 Esp_Vida 0,3788 0,2069 0,2163 -0,0944 Nac_Fuera 0,1002 -0,2374 -0,4168 0,2799 Matrimonios -0,2150 0,0239 -0,0012 -0,5388 Divorcios -0,0483 -0,1074 -0,5434 0,0408 Des_Ingresos -0,2824 0,4067 -0,1314 -0,1339 RiesgoPob_A 0,0526 0,3151 -0,4149 -0,2904 RiesgoPob_D -0,2779 0,4798 -0,0453 -0,1405 GS_PIB 0,3882 0,1130 -0,0294 0,0864 GS_Cápita 0,4246 0,0677 -0,0939 -0,1369 Internet 0,3602 -0,0673 -0,1713 -0,3078 RentaPerCápita 0,3728 0,0872 -0,1083 -0,2595 Tabla 5: Tabla de pesos de las componentes principales. 33 La segunda, tercera y cuarta componente contrapusieron el Acceso a Internet frente a las variables Población e Incremento de población (Figuras 4 - 6). Por otra parte, la segunda y la tercera (Figura 7), fueron las componentes que enfrentaron a dos variables cuyos valores altos eran indicativos de un mayor desarrollo del país en cuestión; se trataba de la Esperanza de vida y el Porcentaje de hogares con acceso a Internet. La cuarta componente fue la única que contrapuso el Porcentaje del PIB dedicado a gasto social con el Gasto social per cápita (Tabla 5 y Figuras 7 - 9). La elevada correlación positiva entre la Renta per cápita y el Gasto social per cápita, se manifestó en que los pesos de las cuatro componentes principales presentaron el mismo signo y además fueron muy similares, para ambas variables. También la variable Riesgo de pobreza antes de recibir transferencias sociales (entiéndase, por transferencias sociales, pensiones y otros tipos de ayudas sociales) presentó el mismo signo en las cuatro componentes principales que dichas variables (Tabla 5 y Figuras 4 - 9). Otras dos variables que presentaron el mismo signo en las cuatro componentes fueron Población e Incremento de población. Por último, la terna Desigualdad en la distribución de los ingresos, Riesgo de pobreza después de recibir transferencias sociales y Matrimonios presentó el mismo signo en los pesos de cada componente, siendo además los pesos muy similares en las dos primeras variables de dicha terna. Representando la primera componente frente a la segunda, tercera y cuarta, respectivamente (Figuras 4 - 6), se observaba la relación entre las variables Esperanza de vida, Porcentaje del PIB destinado a gasto social, Gasto social per cápita, Renta per cápita y Porcentaje de hogares con acceso a Internet. Dichas variables establecían diferencias significativas entre los países de la UE, en función de su pertenencia al primer o segundo grupo resultante del análisis cluster; de hecho, eran las variables que mayores diferencias establecían. 34 Figura 4: Representación bidimensional de la primera componente frente a la segunda. Figura 5: Representación bidimensional de la primera componente frente a la tercera. Figura 6: Representación bidimensional de la primera componente frente a la cuarta. 35 Figura 7: Representación bidimensional de la segunda componente frente a la tercera. Figura 8: Representación bidimensional de la segunda componente frente a la cuarta. Figura 9: Representación bidimensional de la tercera componente frente a la cuarta. 36 4.5. Análisis Factorial Mediante el análisis factorial, se pretendían estudiar relaciones de dependencia entre las variables, expresadas a través de un modelo de factores comunes y únicos. El objetivo, en principio, consistió en averiguar si las 14 variables de población y condiciones de vida se podían resumir en diversos factores que agrupasen las variables comunes. Sin embargo, en este caso, la muestra era demasiado pequeña (se aconseja que el número de variables sea al menos la mitad del número de objetos, y en este caso se tenían 27 objetos, que era el número de países que formaban parte de la UE en el momento del análisis) y el índice KMO = 0,529 desaconsejaba realizar un análisis factorial en estas condiciones, a pesar de que la prueba de Bartlett permitía rechazar, a un nivel de confianza muy cercano al 100 %, la hipótesis de que las variables estuvieran incorreladas. Dado que las variables de tipo demográfico Población, Densidad de población e Incremento de población eran las que presentaban menor correlación con el resto de variables, se optó por cambiar de objetivo y estudiar la relación entre las 11 variables restantes. La medida de adecuación muestral de Kaiser-Meier-Olkin continuó lejos de ser elevada (KMO = 0,578) y la prueba de Bartlett rechazó que la matriz de correlaciones fuese igual a la matriz identidad (χ2 (55) = 246,883; p < 0,001). Se consideraron sólo las cargas factoriales con pesos superiores a 0,30. Utilizando como método de extracción el método de componentes principales y la rotación Varimax, se obtuvo una solución compuesta por tres factores, empleando la regla de Kaiser (dicha regla considera adecuado un número de factores igual al de autovalores de la matriz de correlaciones mayores que la unidad). Dicha solución (Tabla 6) representó casi un 75 % de la variabilidad total. Se observó que en el primer factor tenían mayor peso variables relacionadas con un bienestar económico y social, en el segundo variables relacionadas 37 con desigualdad (y la variable Matrimonios) y en el tercero variables de tipo sociocultural, que podían estar influenciadas por las tradiciones y costumbres religiosas del país. No obstante, dado el peso moderadamente bajo de la variable Matrimonios, se consideró la opción de volver a realizar un análisis factorial sobre las 10 variables restantes, las cuales se consideraron relativas a sociedad y condiciones de vida. Factor 1 GPS per cápita 0,940 Renta per cápita 0,890 Esperanza de vida 0,827 Porcentaje del PIB dedicado al GPS 0,801 Acceso a Internet 0,800 Factor 2 -0,416 0,308 Riesgo de pobreza después de ayudas 0,886 Desigualdad de ingresos 0,862 Riesgo de pobreza antes de ayudas 0,434 Factor 3 0,638 Matrimonios 0,476 Nacidos fuera del matrimonio -0,308 Divorcios 0,390 0,818 0,763 Tabla 6: Matriz de cargas factoriales, mayores que 0,30, tras la rotación Varimax. El nuevo análisis factorial, realizado sobre las 10 variables relativas a sociedad y condiciones de Vida, presentó un KMO = 0,615, mientras que la prueba de Bartlett rechazó que las variables fuesen incorreladas (χ2 (45) = 233,420; p < 0,001). Se volvió a utilizar como método de extracción el método de componentes principales y la rotación Varimax para factores ortogonales, considerando exclusivamente cargas factoriales superiores a 0,30. La solución obtenida (Tabla 7), aplicando la regla de Kaiser, estuvo compuesta por tres factores que explicaron el 80,159 % de la varianza común de las 10 variables sobre las que se realizó el análisis. El primer factor, ya rotado, explicó un 38 41,370 % de esta varianza y estuvo compuesto por variables relativas al bienestar. El segundo factor explicó un 21,590 %, siendo las variables que indicaban ciertas desigualdades sociales las que tenían más peso en este factor. En el tercer factor, fueron variables socioculturales las que tuvieron un mayor peso. Este último factor explicó un 17,198 % de la varianza común. Factor 1 Factor 2 GPS per cápita 0,952 Renta per cápita 0,893 Esperanza de vida 0,842 Porcentaje del PIB dedicado al GPS 0,818 Acceso a Internet 0,814 Riesgo de pobreza después de ayudas -0,331 0,876 Desigualdad de ingresos -0,353 0,869 Riesgo de pobreza antes de ayudas 0,382 0,684 Factor 3 -0,407 0,317 0,369 Nacidos fuera del matrimonio 0,828 Divorcios 0,758 Tabla 7: Matriz de cargas factoriales, mayores que 0,30, de las 10 variables relativas a sociedad y condiciones de vida, tras la rotación Varimax. 5. CONCLUSIONES A pesar de que, tal y como se establecía ya en el Tratado de Roma, la Unión Europea pretende la equidad en materia de bienestar económico y social entre sus estados miembros, existen notables diferencias entre ellos, fundamentalmente entre países que ingresaron con posterioridad a 2004 y países que ya formaban parte de la UE con anterioridad a dicha fecha. En este estudio se ha trabajado con datos correspondientes a 14 variables relativas a población y condiciones de vida; estableciendo, en función de los valores presentados 39 en estas variables, dos grupos de países claramente diferenciados. Así, los países que formaban parte de la Europa de los Quince (con la excepción de Grecia y Portugal) presentaban características muy distintas al grupo de países compuesto por los países del Este protagonistas de las ampliaciones de 2004 y 2007 (con la excepción de Malta), además de Grecia y Portugal. Malta, un país insular en el centro del Mediterráneo, posee unas características especiales que desaconsejan su inclusión en cualquiera de los dos grupos referidos, y hacen necesario considerar un tercer grupo compuesto única y exclusivamente por este estado. Se han encontrado notables diferencias entre el primer y el segundo grupo de países, en las variables Esperanza de vida, Acceso a Internet, Desigualdad de ingresos, Porcentaje del PIB dedicado al gasto en protección social, Gasto en protección social y Renta per cápita, siendo en todos los casos las diferencias favorables al primer grupo. Dicho grupo (que podríamos llamar el de los países más desarrollados dentro de la UE) está constituido además por países con una mayor población total y más densamente poblados, registrando también un mayor incremento de la población al cabo del año estudiado. En base a las variables Acceso a Internet y Gasto social per cápita, que son dos de las variables que mayores diferencias establecen entre los dos grupos principales, se obtiene una buena función discriminante que permite pronosticar que Islandia, Suiza y Noruega pertenecerían al grupo de los países más desarrollados, en el caso de ingresar en la UE. Por otra parte, de ingresar Croacia, Turquía o Macedonia, cualquiera de estos estados formaría parte del segundo grupo. Cuatro parece ser el número de dimensiones adecuado para explicar (sin que se produzca una pérdida notable de información) la variabilidad de las 14 variables inicialmente estudiadas, relativas a población y condiciones de vida. Queda de 40 manifiesto además la relación entre las variables que conforman la terna Renta per cápita - Gasto social per cápita - Riesgo de pobreza antes de recibir transferencias sociales y la alta correlación positiva entre las dos primeras variables de dicha terna. Asimismo, la terna Desigualdad de ingresos - Riesgo de pobreza después de recibir transferencias sociales - Matrimonios presentó indicios de relación entre variables, aunque los pesos de la variable Matrimonios son notablemente distintos (a pesar de tener el mismo signo) a los de las otras dos variables, que sí que presentan una mayor correlación positiva. También el par de variables Población e Incremento de población muestran una fuerte relación, plasmada en el análisis de componentes principales. Realizando un análisis factorial sobre 10 de las variables iniciales, relativas a sociedad y condiciones de vida, subyacen tres factores, relativos a bienestar, desigualdades sociales y características socioculturales, que explican más del 80 % de la varianza común de estas últimas 10 variables. En el primero de ellos, y más importante, las variables Esperanza de vida, Porcentaje del PIB destinado a gasto social, Gasto social per cápita, Renta per cápita y Porcentaje de hogares con acceso a Internet, son las que tienen un mayor peso. La relación entre este grupo de variables queda plasmada en el análisis de componentes principales realizado sobre todas las variables originales, mediante la representación de la primera frente al resto de componentes. El análisis factorial se realizó sobre 10 de las 14 variables iniciales, dado el reducido número de objetos (en este caso, países), que desaconsejaba su empleo para el número inicial de variables, a través del índice KMO. El cambio climático, producido en gran medida por la contaminación, constituye uno de los grandes retos a los que se enfrenta la comunidad internacional, y en particular la Unión Europea, en nuestros días. En este estudio, se observa como, dentro de la UE, los países más poblados son a la postre los que más contaminan (considerando las 41 emisiones totales de CO2). Consideradas tres categorías (alta, media y baja) para las variables Emisiones totales de CO2 y Población, la correspondencia entre ambas variables categóricas es más que notable. El que un país más poblado emita más dióxido de carbono es un hecho obvio cuando los países presentan características más o menos similares y tienen cierto nivel de desarrollo, puesto que una mayor población suele llevar consigo el incremento del consumo de energía y la producción de sustancias contaminantes. De momento, a nivel mundial, la relación entre población total y emisiones de gases contaminantes no es tan fuerte ni tan obvia (tal vez porque las diferencias a nivel de desarrollo son mucho mayores que las existentes en el seno de la Unión Europea). Ahí está el caso de China, que, con casi cinco veces la población de Estados Unidos, emite prácticamente lo mismo (incluso menos) que el país norteamericano. India es otro ejemplo similar, aunque en este caso sus emisiones de dióxido de carbono son notablemente inferiores a las de Estados Unidos. 42 6. REFERENCIAS AEMA (1998); Europe’s Environment: The Second Assesment. Luxemburgo: Oficina de Publicaciones Oficiales de las Comunidades Europeas. AEMA (2004); Señales medioambientales de la AEMA. Luxemburgo: Oficina de Publicaciones Oficiales de las Comunidades Europeas. Anderson, T.W. (1984); An introduction to multivariate statistical analysis. Nueva York: Wiley. Banco Central Europeo (2007); La UE ampliada y las economías de la zona del Euro. Boletín Mensual del Banco Central Europeo, 1, 59-66. Bartiaux, F., Van Ypersele, J.P. (1993). The role of population growth in global warming. International Population Conference. Montreal. International Union for the Scientific Study of Population, 4, 33-54. Benzécri, J.P. (1982); L´analyse des données. II, L´analyse des correspondances. París: Dunod. Bernstein, I.H. (1987); Applied multivariate analysis. Nueva York: Springer. Cuadras, C.M. (1991); Métodos de análisis multivariante. Barcelona: PPU. Cancelo, M.T., Díaz, M.R. (2002); Emisiones de CO2 y crecimiento económico en países de la UE. Estudios Económicos de Desarrollo Internacional. AEEADE. 2, 1. Comisión Europea (2007); Hechos y cifras clave sobre Europa y los europeos. Luxemburgo: Oficina de Publicaciones Oficiales de las Comunidades Europeas. http://www.ec.europa.eu/publications/booklets/eu_glance/51/es.pdf consultada el 5 de septiembre de 2009. Comisión Europea (2008); Acción de la UE contra el cambio climático. El régimen de comercio de derechos de emisión de la UE. Luxemburgo: Oficina de Publicaciones Oficiales de las Comunidades Europeas http://www.ec.europa.eu/environment/climat/pdf/brochures/ets_es.pdf consultada el 5 de septiembre de 2009. De Esteban, F. (1994); Eurostat, la oficina estadística de la Comisión Europea. Quaderns d'Estadistica, Sistemes, Informatica i Investigació Operativa, 18, 2, 231-240. Dietz, T., Rosa, E.A. (1997); Effects of population and affluence on CO2 emissions. Proceedings of the National Academy of Sciences of the United States of America, 94, 175-179. Ehrlich, P., Holdren, J. (1971); The impact of population growth. Science, 171, 1212-1217. Eurostat (2008); Living conditions in Europe: Data 2003-06. Eurostat pocketbooks. Luxemburgo: Office for official publications of the European Communities. Ezcurra, R., Pascual, P., Rapún, M. (2007); The spatial distribution of income inequality in the European Union. Environment and Planning A, 39, 869-890. Fontaine, P. (2003); Doce lecciones sobre Europa. Bruselas: Comisión Europea. http://www.ec.europa.eu/publications/booklets/eu_glance/22/es.pdf consultada el 5 de septiembre de 2009. 43 Gaffin, S.R., O´Neill, B.C. (1997); Population and global warming with and without CO2 targets. Population and Environment, 18, 4, 389-413. García, E., Gil, J., Rodríguez, G. (2000); Análisis factorial. Cuadernos de Estadística. Madrid: La Muralla. Gil, J., García, E., Rodríguez, G. (2001); Análisis discriminante. Cuadernos de Estadística. Madrid: La Muralla. Giannakouris, K. (2008); Ageing characterises the demographic perspective of the European societies. Population and social conditions. Eurostat, Statistics in focus, 72/2008. http://epp.eurostat.ec.europa.eu/cache/ITY_OFFPUB/KS-SF-08-072/EN/KS-SF-08-072EN.PDF consultada el 5 de septiembre de 2009. Greenacre, M. (2008); La práctica del análisis de correspondencias. Bilbao: Fundación BBVA. http://www.fbbva.es/TLFU/tlfu/ing/publicaciones/libros/fichalibro/index.jsp?codigo=300 consultada el 5 de septiembre de 2009. Hair, J.F., Anderson, R.E., Tatham, R.L., Black, W.C. (1995); Multivariate data analysis. 4th ed. Englewood Cliffs, NJ: Prentice Hall. Harte, J. (2007); Human population as a dynamic factor in environmental degradation. Population and Environment, 28, 223-236. Instituto Nacional de Estadística (2008); España en la UE de los 27. Madrid: INE. http://www.ine.es/prodyser/pubweb/espue27/espue27.htm consultada el 5 de septiembre de 2009. Joaristi, L., Lizasoain, L. (2000); Análisis de correspondencias. Cuadernos de Estadística. Madrid: La Muralla. Kaiser, H. F. (1958); The varimax criterion for analytic rotation in factor analysis. Psychometrika, 23, 3, 187-200. Kendall, M.G. (1980); Multivariate analysis. 2nd ed. Londres: Charles Griffin. Klecka, W.R. (1982); Discriminant analysis. Londres: Sage. MacKellar, F.L., Lutz, W., Prinz, C., Goujon, A. (1995); Population, households and CO2 emissions. Population and Development Review, 21, 4, 849-865. Martín, J.J. (2005); La Unión Europea ante el fenómeno del cambio climático. Burgos: Servicio de Publicaciones de la Universidad de Burgos. Martín, R., Pérez, G.A. (2003); Historia de la Unión Europea: de los Seis a la ampliación al Este. Cuadernos de Historia. Madrid: Arco Libros. Martínez, R. (1999); El análisis multivariante en la investigación científica. Cuadernos de Estadística. Madrid: La Muralla. Martínez, I., Bengoechea, A., Morales, R. (2007). The impact of population on CO2 emissions: evidence from European countries. Environmental and Resource Economics, 38, 4, 497-512. Maxwell, A.E. (1977); Multivariate analysis in behavioural research. Nueva York: Wiley. 44 Morrison, D.F. (1976); Multivariate statistical methods. Nueva York: Mc Graw-Hill. Murtaugh, P.A., Schlax, M.G. (2009); Reproduction and the carbon legacies of individuals. Global Environment Change, 19, 14-20. Nieto, J. (2005); Cambio climático y Protocolo de Kioto: efectos sobre el empleo, la salud y el medio ambiente. Información Comercial Española, ICE: Revista de economía, 822, 25-38. Notestein, Frank W. (1945); "Population: the long view", in Schultz, T. W. (ed.), Food for the world, Chicago: Chicago University Press, pp. 36-57. Onozaki, K. (2009); Population is a critical factor for global carbon dioxide increase. Journal of Health Science, 55, 1, 125-127. Puglia, A. (2009); In 2006, gross expenditure on social protection accounted for 26.9 % of GDP in the EU-27. Population and social conditions. Eurostat, Statistics in focus, 40/2009. http://epp.eurostat.ec.europa.eu/cache/ITY_OFFPUB/KS-SF-09-040/EN/KS-SF-09-040EN.PDF consultada el 5 de septiembre de 2009. Puyol, R., Vinuesa, J. (1997); La Unión Europea. Madrid: Editorial Síntesis. Rivas, T., Rius, F., Martínez, R. (1990); Análisis discriminante: una aplicación del método “Stepwise”. Málaga: Universidad de Málaga. Rychtarikova, J. (2007); “Differents risks of population ageing: EU old and new members”, chapter 6 in Dostál, P. (ed.), Evolution of geographical systems and risk processes in global context. Praga: p3k. http://www.natur.cuni.cz/geografie/vzgr/monografie/evolution/evolution_rychtarikova.pdf consultada el 5 de septiembre de 2009. Shi, A. (2001); Population Growth and Global Carbon Dioxide Emissions. Conference in Brazil. www.iussp.org/Brazil2001/s00/S09_04_Shi.pdf consultada el 5 de septiembre de 2009. Tabachnick, B.G., Fidell, L.S. (1996); Using multivariate statistics. Nueva York: Harper Collins. Tamames, R. (1994); La Unión Europea. Madrid: Alianza Editorial. Termes, R. (2003); La Unión Europea: historia y perspectivas. http://web.iese.edu/Rtermes/acer/files/escorial2003.pdf consultada el 5 de septiembre de 2009. Visauta, B. (1998); Análisis estadístico con SPSS para Windows. Volumen II: Estadística multivariante. Madrid: Mc Graw-Hill. Welsch, H., Bonn, U. (2008); Economic convergence and life satisfaction in the European Union. The Journal of Socio-Economics, 37, 1153-1167. 45